- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение теории вероятностей в анализе спортивных событий презентация
Содержание
- 1. Применение теории вероятностей в анализе спортивных событий
- 2. Событие – любой факт, который может произойти
- 3. 3 Виды событий
- 4. 4 Случайные события
- 5. Зависимые и независимые события 5 События бывают
- 6. Вероятностью события А называется отношение числа благоприятствующих
- 7. Условная вероятность Если событие В зависит от
- 8. Сумма, произведение событий Суммой двух событий
- 9. 9 Найти вероятность совместного появления герба при
- 10. 10 Планируемая работа Проведение статистического анализа по
- 11. Спасибо за внимание! 11
Слайд 2Событие – любой факт, который может произойти или не произойти в
2
Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка).
Что такое теория вероятностей.
Слайд 5Зависимые и независимые события
5
События бывают зависимыми и независимыми.
Событие В называется
Событие В называется зависимым от события А, если его вероятность Р(В) меняется в зависимости от того, произошло событие A или не произошло.
Слайд 6Вероятностью события А называется отношение числа благоприятствующих этому событию исходов m
Р(А)=m/n, 0<=Р(А)<=1
Пример:
Р(А)=1/2;
Р(А)=1/6.
5
Определение вероятности
Слайд 7Условная вероятность
Если событие В зависит от события А, то условной вероятностью
Условная вероятность в этом случае обозначается Р(В/А). Если событие В не зависит от события А, то выполняется равенство Р(В/А) = Р(В).
7
Слайд 8Сумма, произведение событий
Суммой двух событий А и В называется событие А+В,
Произведением нескольких событий называется событие, которое состоит в совместном появлении всех этих событий.
8
Слайд 99
Найти вероятность совместного появления герба при одновременном бросании двух монет. Вероятность
Перед кабинетом врача 30 пациентов: 5 мужчин, 10 женщин, 15 старушек. Какова вероятность того, что первый вошедший в кабинет будет мужчина или женщина?
Пусть событие А - это появление мужчины, событие В - это появление женщины.
Тогда вероятность появления мужчины равна Р(А) = 5/30 = 1/6. Вероятность появления женщины равна Р(В) = 10/30 = 1/3.
События А и В несовместны, так как появление мужчины исключает появление женщины.
Искомая вероятность равна Р(А) + Р(В)=1/6 + 1/3 = 1/2
Примеры
Слайд 1010
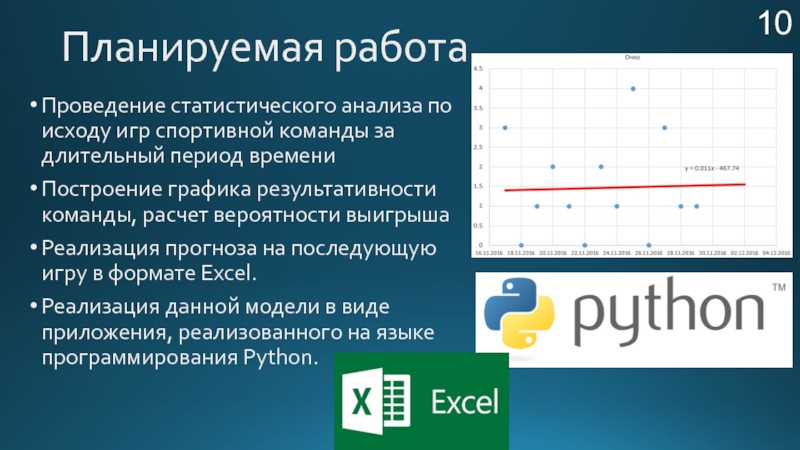
Планируемая работа
Проведение статистического анализа по исходу игр спортивной команды за длительный
Построение графика результативности команды, расчет вероятности выигрыша
Реализация прогноза на последующую игру в формате Excel.
Реализация данной модели в виде приложения, реализованного на языке программирования Python.