- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение теории графов к решению задач презентация
Содержание
- 1. Применение теории графов к решению задач
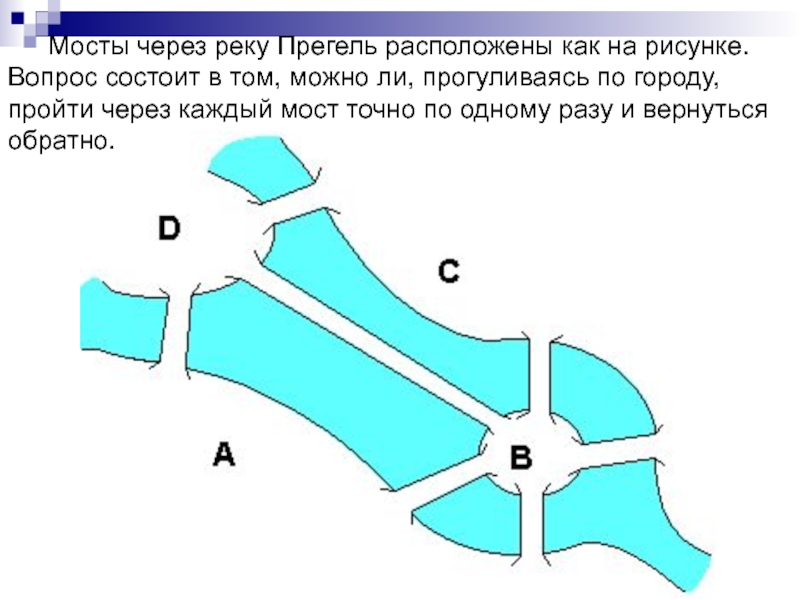
- 2. Мосты через реку Прегель расположены как
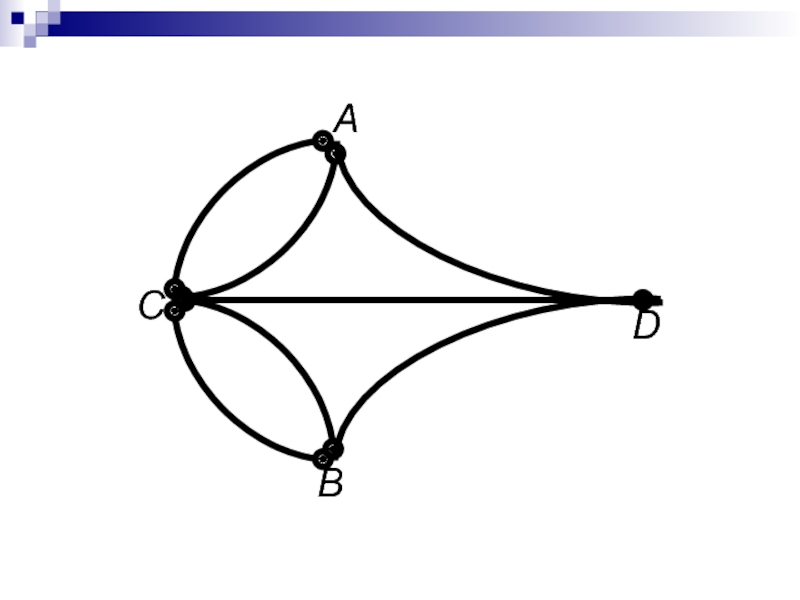
- 3. D
- 4. На рисунке изображена решетка. Можно ли провести
- 5. Виды графов: Неориентированный граф Ориентированный граф
- 6. Неориентированные графы
- 7. Задача 1. В шахматном турнире участвовали
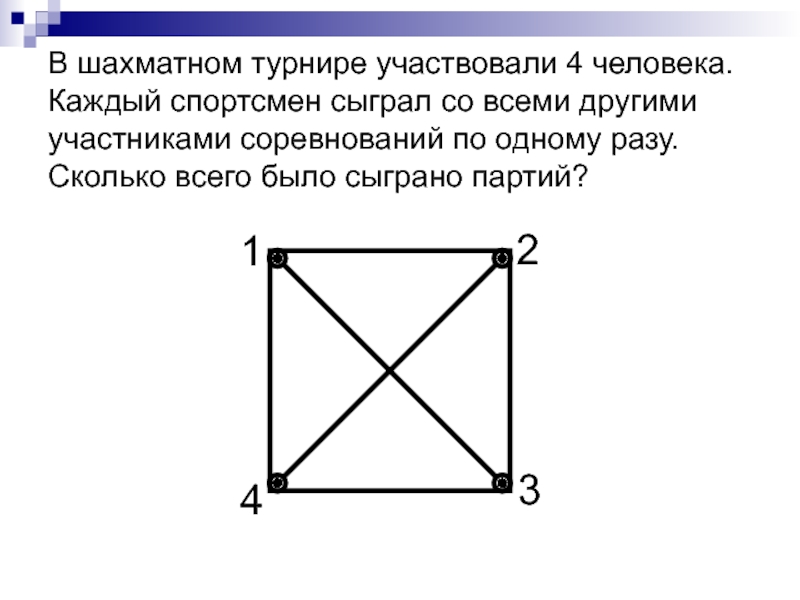
- 8. В шахматном турнире участвовали 4 человека.
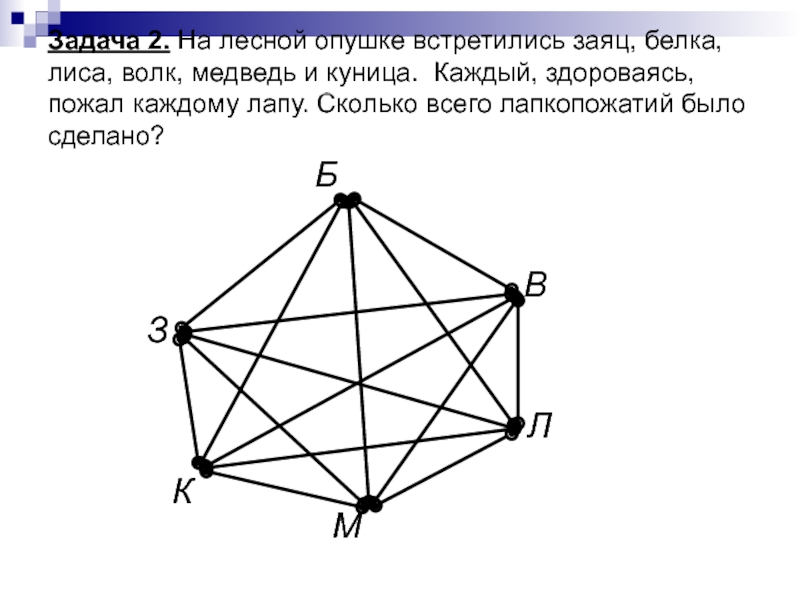
- 9. Задача 2. На лесной опушке встретились
- 10. Задача
- 11. Несколько мальчиков встретились на вокзале, чтобы
- 12. Задача 3. Несколько мальчиков встретились на
- 13. Несколько мальчиков встретились на вокзале, чтобы
- 14. Несколько мальчиков встретились на вокзале, чтобы
- 16. Д Б В А
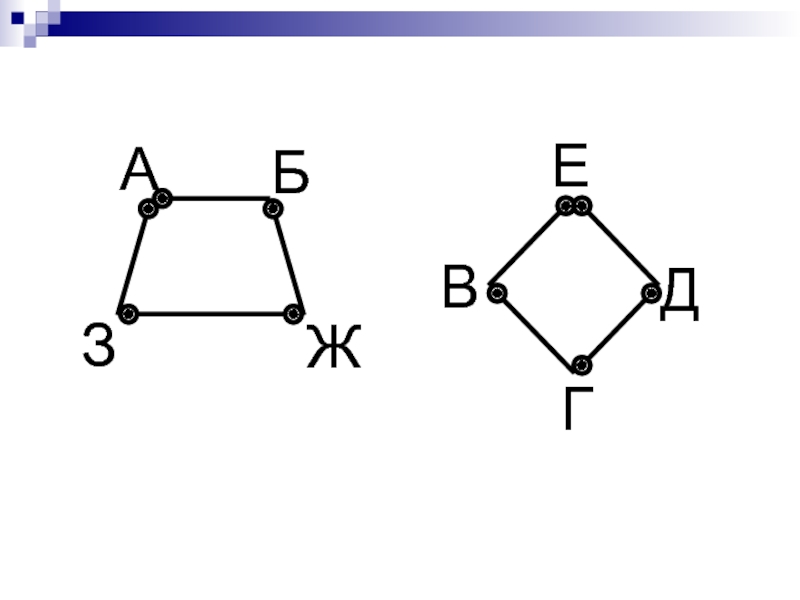
- 17. Задача 5. В стране алфавит 8 городов:
- 18. А Г Д В Ж З Б Е
- 19. Ориентированные графы
- 20. Задача
- 21. Вася идет впереди
- 23. Т
- 25. Д Л Я Т К С Р
- 26. Граф-дерево или дерево возможностей
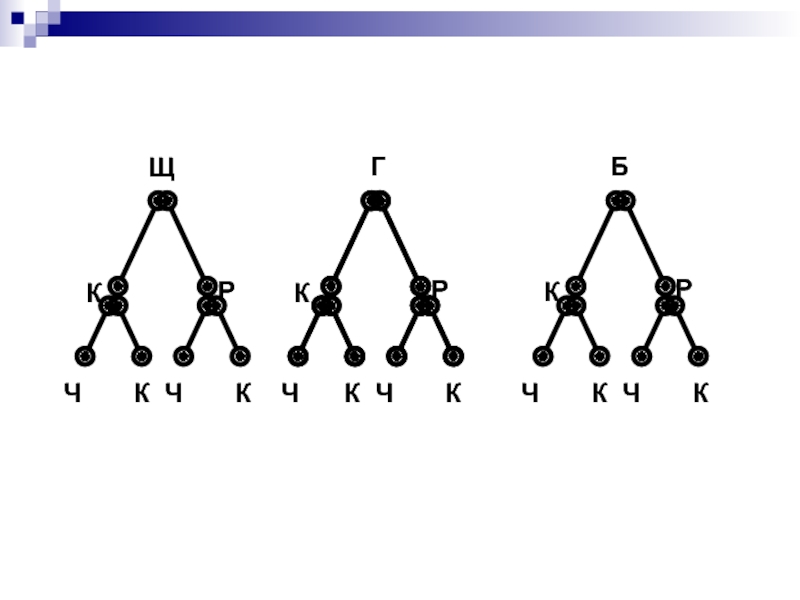
- 27. Задача 9.
- 28. Р К Ч
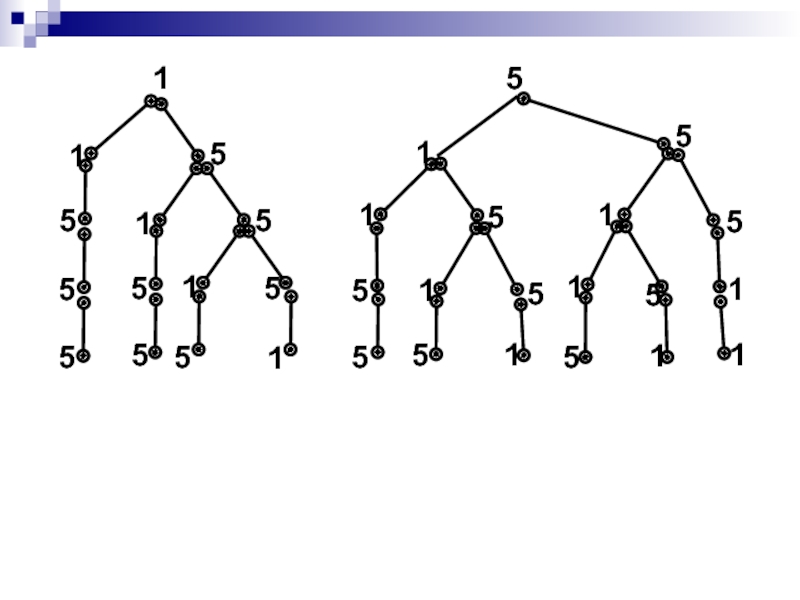
- 30. 1
- 31. Граф с ребрами двух цветов
- 32. Задача
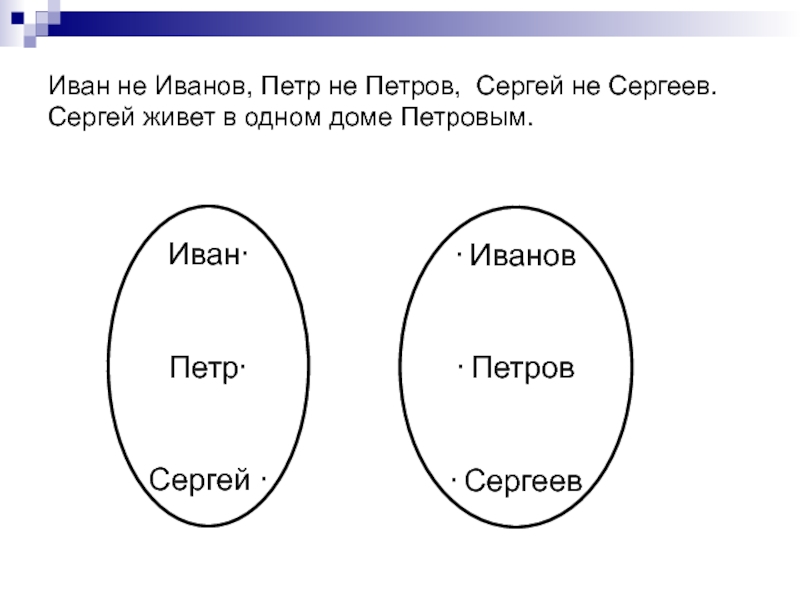
- 33. Иван не Иванов, Петр не Петров, Сергей
- 35. Щенок Алеши темнее по окрасу, чем ротвейлер,
- 36. Щенок Алеши темнее по окрасу, чем ротвейлер,
- 37. Щенок Алеши темнее по окрасу, чем ротвейлер,
Мосты через реку Прегель расположены как на рисунке. Вопрос состоит в том, можно ли, прогуливаясь по городу, пройти через каждый мост точно по одному разу и вернуться обратно.
Слайд 2
Мосты через реку Прегель расположены как на рисунке. Вопрос состоит в
том, можно ли, прогуливаясь по городу, пройти через каждый мост точно по одному разу и вернуться обратно.
Слайд 4На рисунке изображена решетка. Можно ли провести непрерывную линию, пересекающую точно
по разу каждую сторону решетки?
Слайд 5Виды графов:
Неориентированный граф
Ориентированный граф
Граф-дерево или дерево возможностей
Граф с ребрами
двух цветов
Слайд 7Задача 1. В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл
со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий?
Слайд 8 В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми
другими участниками соревнований по одному разу. Сколько всего было сыграно партий?
1
2
3
4
Слайд 9 Задача 2. На лесной опушке встретились заяц, белка, лиса, волк, медведь
и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкопожатий было сделано?
Б
М
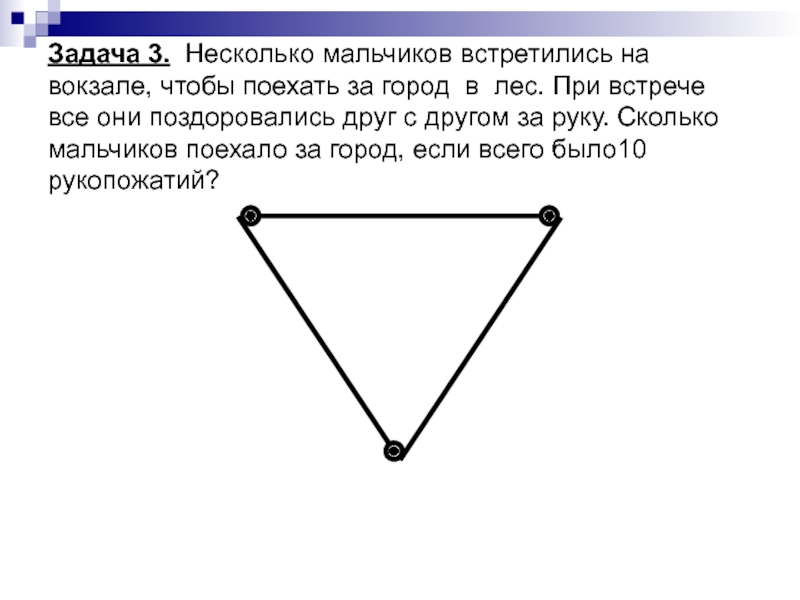
Слайд 10 Задача 3. Несколько мальчиков встретились на вокзале, чтобы поехать за город
в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
Слайд 11 Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес.
При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
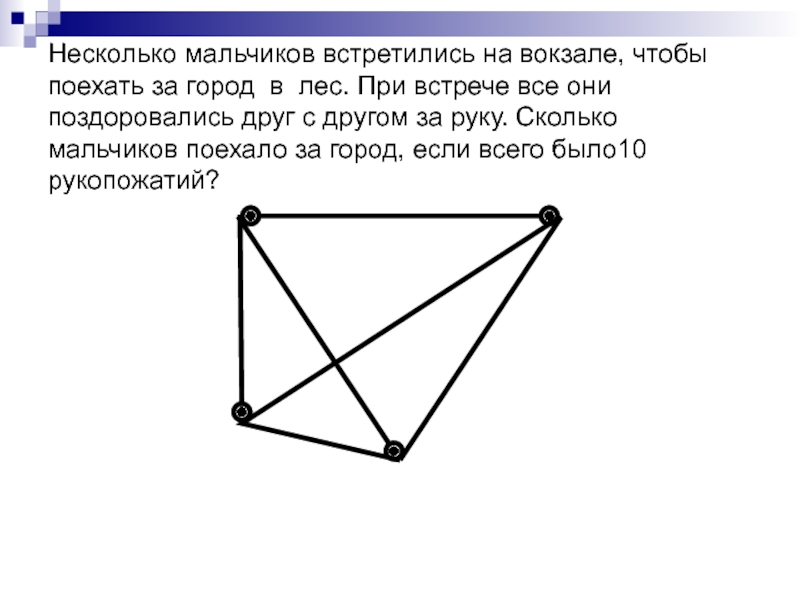
Слайд 12 Задача 3. Несколько мальчиков встретились на вокзале, чтобы поехать за город
в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
Слайд 13 Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес.
При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
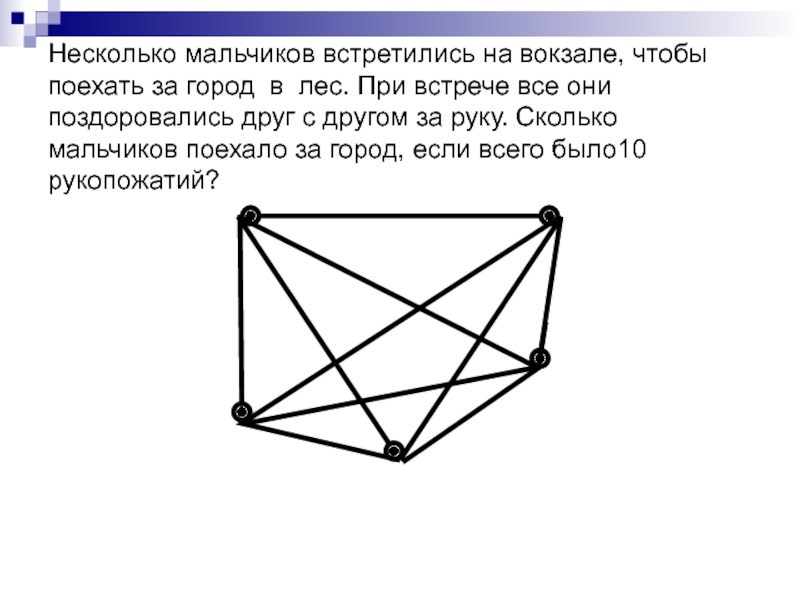
Слайд 14 Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес.
При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
Слайд 15 Задача 4. В первенстве класса по шашкам 5 участников: Аня, Боря,
Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?
Слайд 16Д
Б
В
А
Г
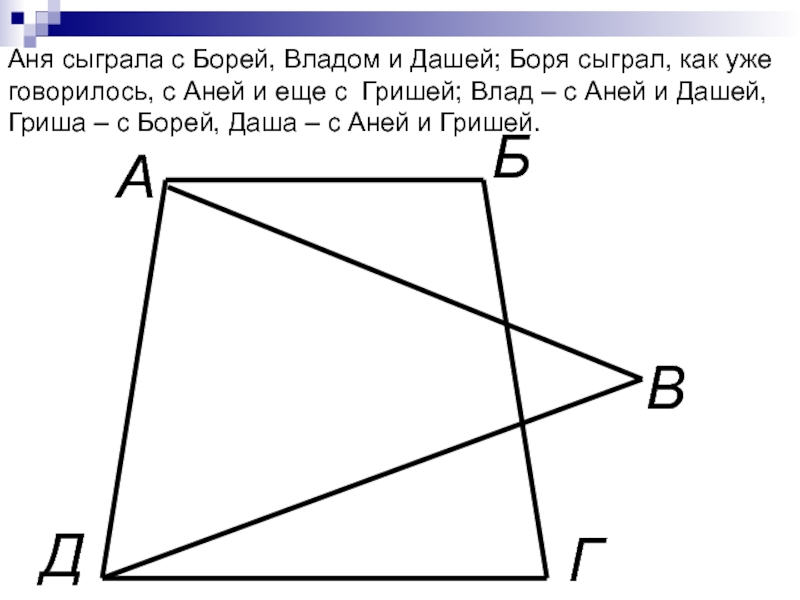
Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже
говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей.
Слайд 17Задача 5. В стране алфавит 8 городов: А, Б, В, Г,
Д, Е, Ж, З и восемь непересекающихся дорог между городами А и Б,
Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е. Можно ли по этим дорогам проехать из А в Г?
Слайд 20 Задача 6. Из лагеря вышли четыре туриста: Вася, Галя, Толя и
Лена. Вася идет впереди Лены, Толя впереди Гали, а Лена впереди Толи. В каком порядке идут дети?
Вася Лена
Толя
Галя
Слайд 22 Задача 7. В детском лагере отдыха в одной комнате живут четыре
девочки: Маша, Валя, Таня и Галя. Две из них ровесницы. Известно, что Таня старше Маши, которая моложе Гали. Таня моложе Вали, которая старше Гали. Кто ровесницы?
Т
М
Г
Г
В
Слайд 24 Задача 8. На пришкольном участке растут 8 деревьев: яблоня, тополь, береза,
рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Слайд 25Д
Л
Я
Т
К
С
Р
Б
Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше
сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони.
Слайд 27 Задача 9. В столовой на горячее можно заказать щуку, грибы и
баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд?
Слайд 29 Задача 10. Из наборного полотна взяли 2 карточки с цифрой 1
и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?
Слайд 32 Задача 12. В одном классе учатся Иван, Петр и Сергей. Их
фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым.
Слайд 33Иван не Иванов, Петр не Петров, Сергей не Сергеев. Сергей живет
в одном доме Петровым.
Иван∙
Петр∙
Сергей ∙
∙ Иванов
∙ Петров
∙ Сергеев
Слайд 34 Задача 13. Три друга – Алеша, Сергей и Денис – купили
щенков разной породы: щенка ротвейлера, щенка колли и щенка овчарки. Известно, что: щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.
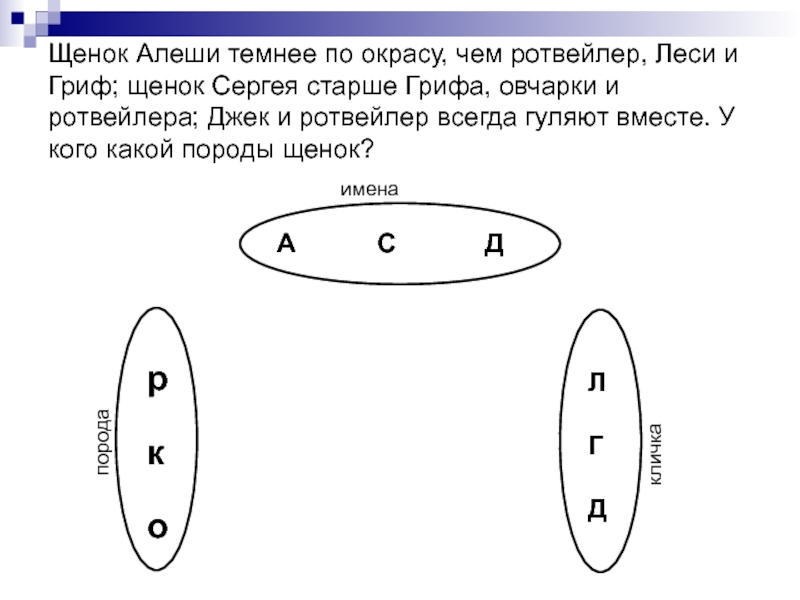
Слайд 35Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок
Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок?
А С Д
р
к
о
имена
порода
кличка
Л
Г
Д
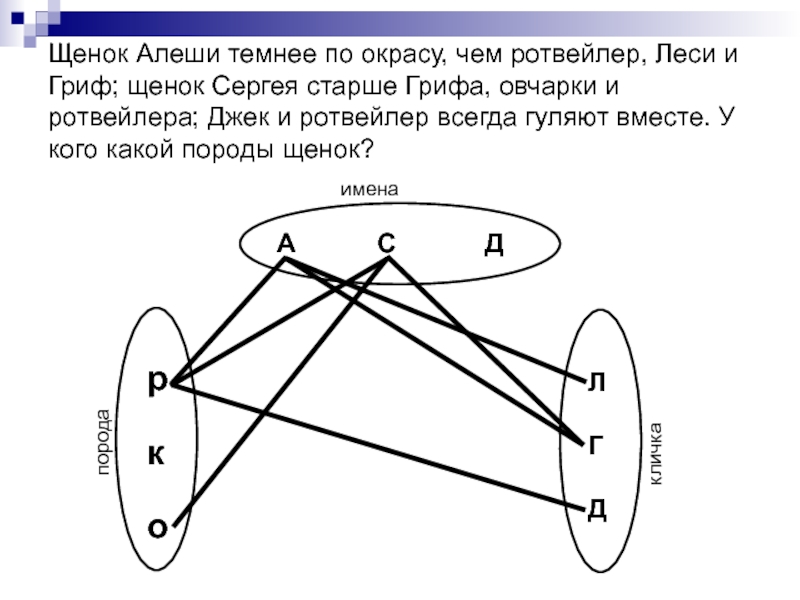
Слайд 36Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок
Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок?
А С Д
р
к
о
имена
порода
кличка
Л
Г
Д
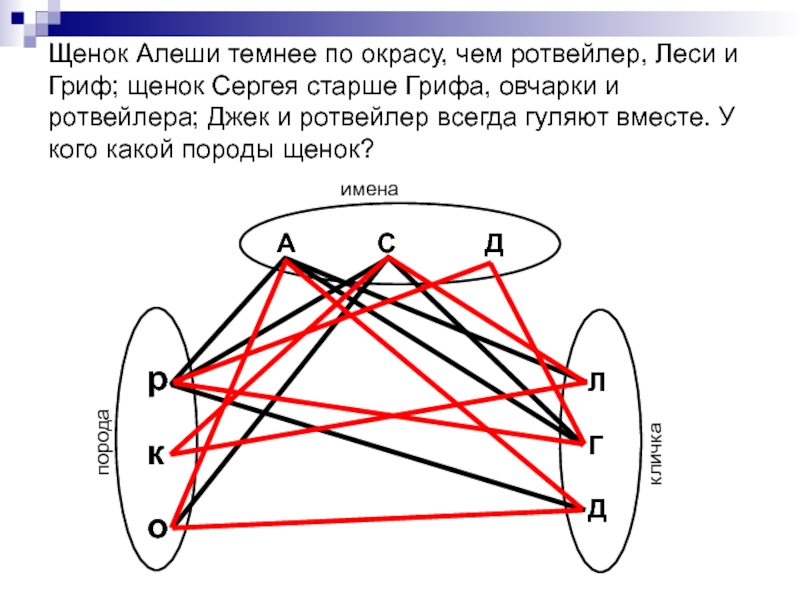
Слайд 37Щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок
Сергея старше Грифа, овчарки и ротвейлера; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок?
А С Д
р
к
о
имена
порода
кличка
Л
Г
Д
