- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение дифференциала для приближенных вычислений. (Лекция 2) презентация
Содержание
- 1. Применение дифференциала для приближенных вычислений. (Лекция 2)
- 2. Применение дифференциала для приближенных вычислений. Из определения
- 3. Пример: вычислить без таблицы Sin29 ͦ Sin29
- 4. Частные производные функций
- 5. Частные и полный дифференциал функции
- 6. Задача: найдите абсолютную погрешность в определении объема
- 7. Интегральное исчисление. Первообразная функция. Функция F(x)
- 8. Неопределенный интеграл. Определение: Неопределенным интегралом функции
- 10. Свойства: где u,
- 11. Методы интегрирования А) Непосредственное интегрирование.
- 12. Б) Способ подстановки (замены переменных).
- 13. В) Интегрирование по частям.
- 14. Пример. Видно, что в результате
- 16. Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)
- 17. Найдем значения функции в этих точках и
- 18. Свойства определенного интеграла. 4. Если f(x) ≤
- 19. 5.Если m и M – соответственно наименьшее
- 20. 8. Для произвольных чисел a, b, c
- 21. Пример.
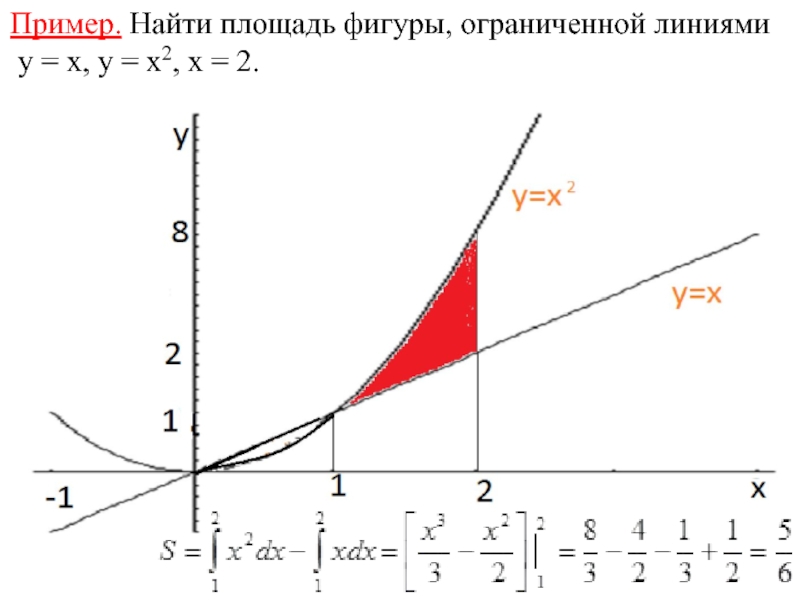
- 22. Пример. Найти площадь фигуры, ограниченной линиями
- 23. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 24.
- 25.
Слайд 2Применение дифференциала для приближенных вычислений.
Из определения производной функции:
Можно записать:
или .
Величина - бесконечно малая более высокого порядка, чем f’(x)Δx, т.е. f'(x)Δx- главная часть приращения у. Отбрасывая вторую часть в этой формуле, можем написать: Δy=f’(x)Δx или f(x+Δx)-f(x)=f’(x)Δx; отсюда можем вычислить значение функции в точке x+Δx: f(x+Δx)=f(x)+f’(x)Δx; если f(х) и f’(x) можно легко вычислить в точке x.
αΔx
Слайд 3Пример: вычислить без таблицы Sin29 ͦ
Sin29 ͦ=Sin(30 ͦ-1 ͦ), поэтому примем
Sin29 ͦ=Sin30 ͦ+Cos30 ͦ(-0,017)=0,485.
1 ͦ=3,14/180=0,017
Sin’x=Cosx
Вычислите без таблицы lg101.
Слайд 6Задача: найдите абсолютную погрешность в определении объема цилиндра, если при измерениях
Слайд 7Интегральное исчисление.
Первообразная функция.
Функция F(x) называется первообразной функцией функции f(x) на отрезке
F′(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
Слайд 8Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые
F(x) + C.
Записывают:
Слайд 14Пример.
Видно, что в результате повторного применения интегрирования по частям функцию
Слайд 17Найдем значения функции в этих точках и составим выражение, которое называется
Sn = f(ε1)Δx1 + f(ε2)Δx2 + … + f(εn)Δxn =
Внутри каждого отрезка выберем некоторую точку ε.
x0 < ε1 < x1, x1 < ε2 < x2, … , xn-1 < εn < xn.
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxΔxi→ 0 и произвольном выборе точек εi интегральная сумма
стремится к пределу S, который называется опреде-
ленным интегралом от f(x) на отрезке [a, b]:
Слайд 195.Если m и M – соответственно наименьшее и наибольшее значения функции
6. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка ε такая, что
Слайд 208. Для произвольных чисел a, b, c справедливо равенство:
Теорема: (Теорема Ньютона






![Интегральное исчисление.Первообразная функция.Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в](/img/tmb/5/432081/98814ff59b1490458bae0ba9015139bd-800x.jpg)






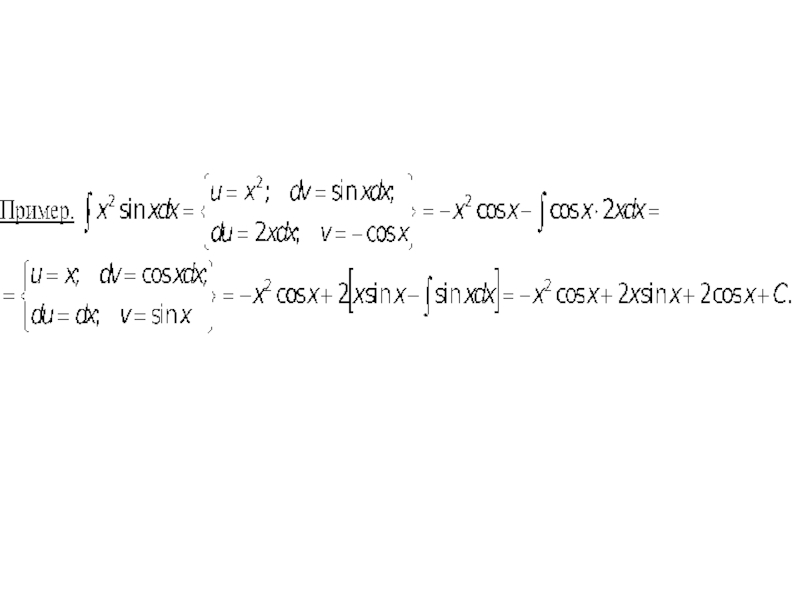
![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/img/tmb/5/432081/1f438896af91d53608a4a6a08f04fbd5-800x.jpg)

![Свойства определенного интеграла.4. Если f(x) ≤ ϕ(x) на отрезке [a, b] a < b, то](/img/tmb/5/432081/12c1f44f05895385cc1ef4322e406c6f-800x.jpg)