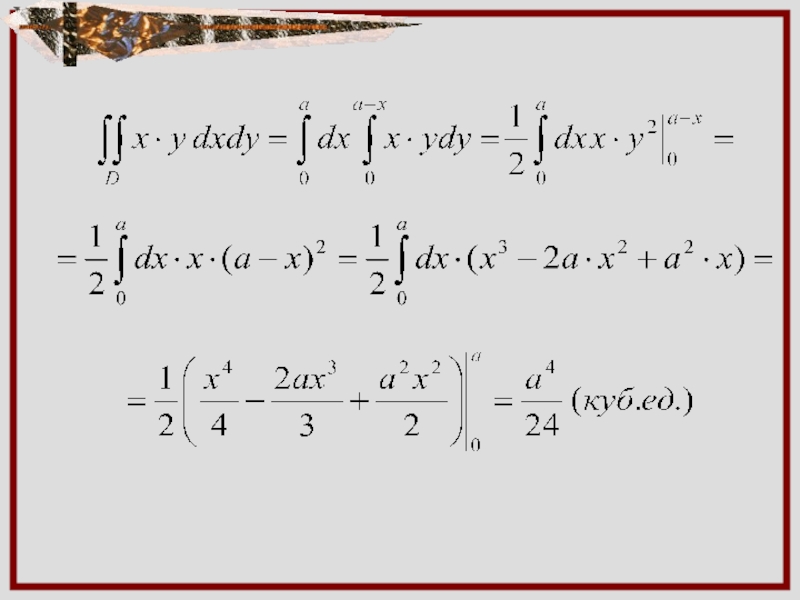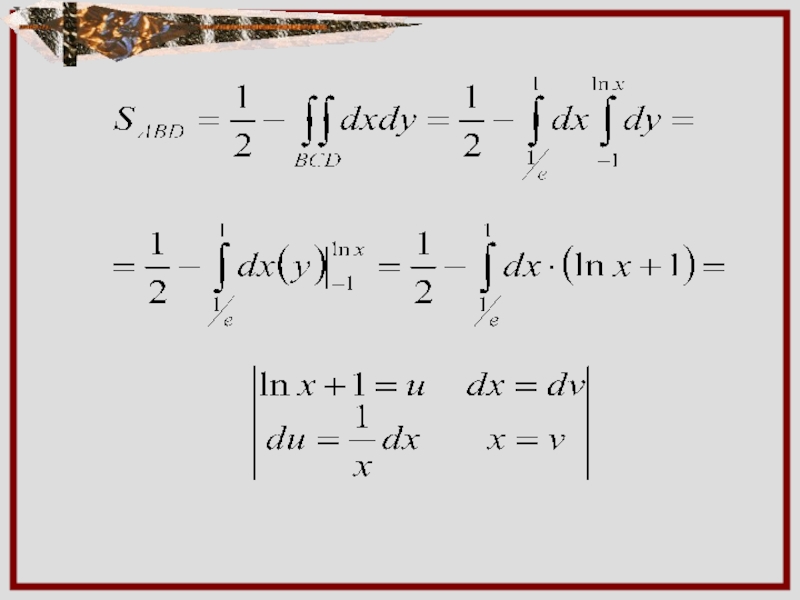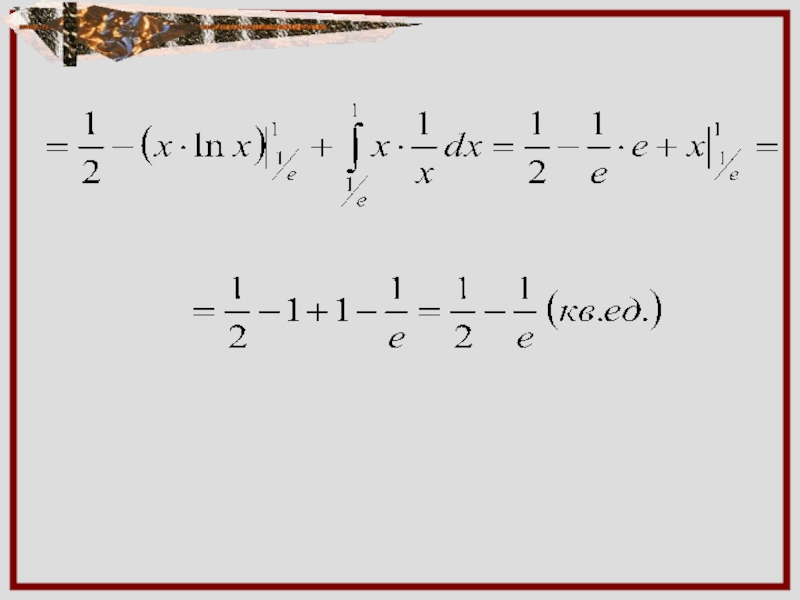интеграла следует, что любой двойной интеграл задает объем тела, ограниченного сверху графиком подынтегральной функции, снизу – областью D, с боков – цилиндрической поверхностью с направляющими по границе области D.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приложения двойного интеграла. Вычисление объемов тел презентация
Содержание
- 1. Приложения двойного интеграла. Вычисление объемов тел
- 2. Пример. Вычислить объем тела, ограниченного поверхностями
- 3. Решение. Поскольку подынтегральная функция должна быть не
- 5. 2. Вычисление площадей фигур Площадь некоторой области D может быть найдена по формуле:
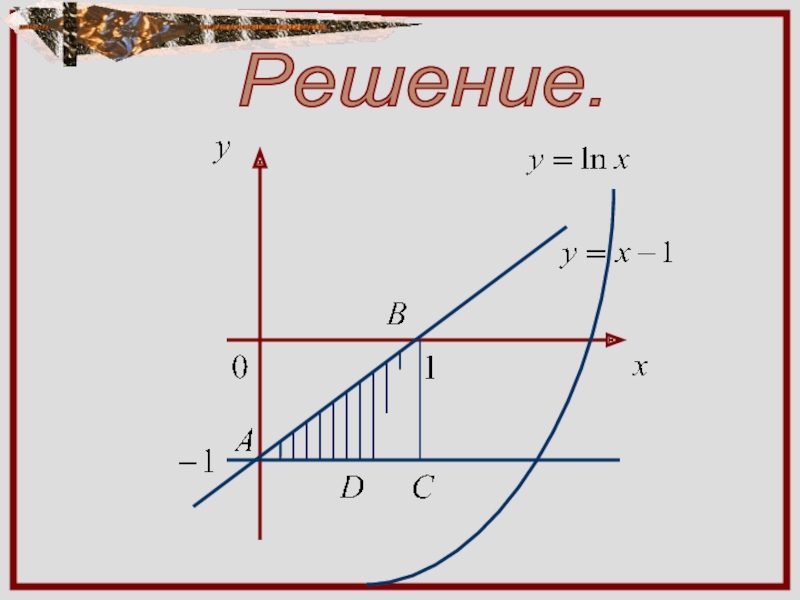
- 6. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 7. Решение.
- 8. площадь прямоугольного треугольника, катеты которого равны 1.
Пример. Вычислить объем тела, ограниченного поверхностями
Слайд 117.6. ПРИЛОЖЕНИЯ
ДВОЙНОГО ИНТЕГРАЛА
1. Вычисление объемов тел
Из геометрического смысла двойного
Слайд 3Решение.
Поскольку подынтегральная функция должна быть не отрицательна, то область интегрирования ограничена
на плоскости ХОУ прямоугольным равнобедренным треугольником с катетами, равными а.
Слайд 8площадь прямоугольного треугольника,
катеты которого равны 1.
ограничена снизу прямой y=-1 при
сверху кривой
y=lnx и справа прямой x=1.
