- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приближенные методы вычислений презентация
Содержание
- 1. Приближенные методы вычислений
- 2. Многие научные и инженерные задачи описываются с
- 3. Приближенные методы решения задач предполагают вычисление не
- 4. Вычисление корня функции методом деления отрезка пополам
- 5. Часто в задачах необходимо решать уравнения вида
- 6. Отделение корней (т.е.определение интервала изменения переменной
- 7. Отделение корней графическим методом Если из
- 8. Уточнение корней методом половинного деления Пусть
- 9. Метод построен на вычислении середины отрезка
- 10. Приближенное вычисление интеграла
- 11. Определённый интеграл Можно трактовать как площадь
- 12. В простейшем случае, когда известна первообразная F(x),
- 13. Пусть функция f(x) определена на отрезке
- 14. Метод левых прямоугольников Если для вычисления
- 15. Метод правых прямоугольников Если для вычисления
- 16. Метод трапеций Если построить не прямоугольники,
- 17. Метод Монте-Карло
- 18. Остроумный метод приближенного вычисления площадей сложных фигур
- 19. Дана фигура сложной формы. Требуется: вычислить площадь
- 20. Таким образом, при большом числе точек доля
Слайд 2Многие научные и инженерные задачи описываются с помощью таких математических моделей,
В таких случаях для решения подбираются различные методы приближенных вычислений и разрабатываются алгоритмы их реализации на ЭВМ.
Слайд 3Приближенные методы решения задач предполагают вычисление не точного искомого решения, а
Слайд 5Часто в задачах необходимо решать уравнения вида f(x)=0.
Только для простейших уравнений
Чаще уравнения приходится решать приближенными (численными) методами.
Слайд 6 Отделение корней (т.е.определение интервала изменения переменной x, где расположен 1
Уточнение корней (т.е. определение корней с заданной точностью)
Этапы численного решения уравнений
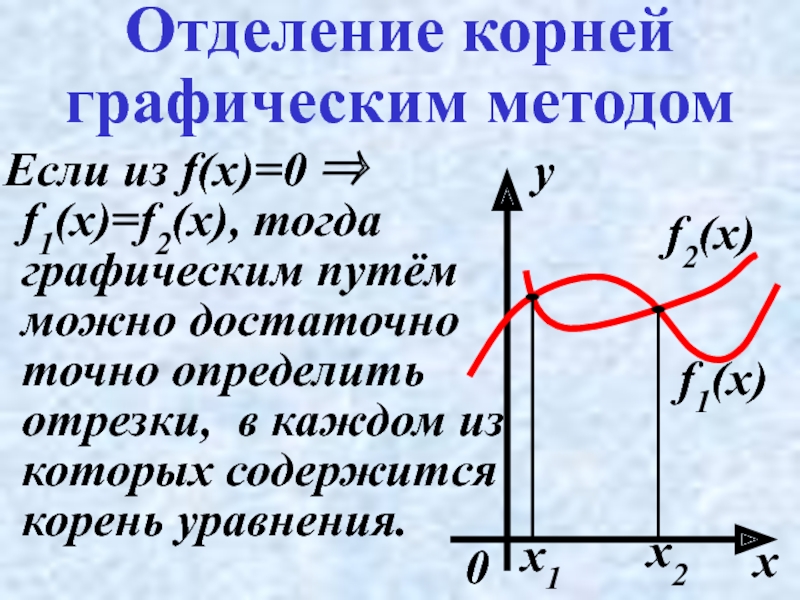
Слайд 7Отделение корней графическим методом
Если из f(x)=0 ⇒ f1(x)=f2(x), тогда графическим
x
у
0
f1(x)
f2(x)
x1
x2
Слайд 8Уточнение корней методом половинного деления
Пусть f(x) определена на [а,b], непрерывна
Требуется: найти корень f(x)=0 с заданной точностью (погрешностью) ε
Слайд 9 Метод построен на вычислении середины отрезка с=(а+b)/2 и выборе из
x
у
0
f (x)
a
b
Суть метода
с
Слайд 11Определённый интеграл
Можно трактовать как площадь подынтегральной функции (криволинейной трапеции) на
x
у
0
f(x)
a
b
= S
Слайд 12В простейшем случае, когда известна первообразная F(x), интеграл вычисляется по формуле
Для большинства функций нахождение первообразной сложно или невозможно. Тогда применяется приближённое (численное) интегрирование.
= F(b)-F(a)
Слайд 13 Пусть функция f(x) определена на отрезке [а;b].
Требуется: приближенно вычислить определённый
Суть метода: разобьём отрезок [а,b] на n равных отрезков длины h=(b-a)/n, разрезая фигуру под функцией f(x) на n полосок, считая их прямоугольниками.
Тогда S ≈ Si , при n→∞ Si → S
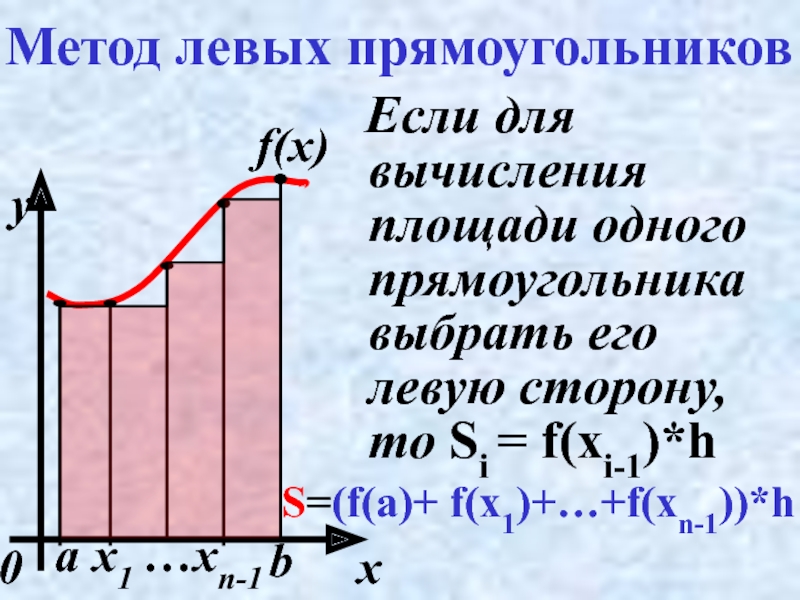
Слайд 14Метод левых прямоугольников
Если для вычисления площади одного прямоугольника выбрать его
x
у
0
f(x)
a
b
S=(f(a)+ f(x1)+…+f(xn-1))*h
x1
xn-1
…
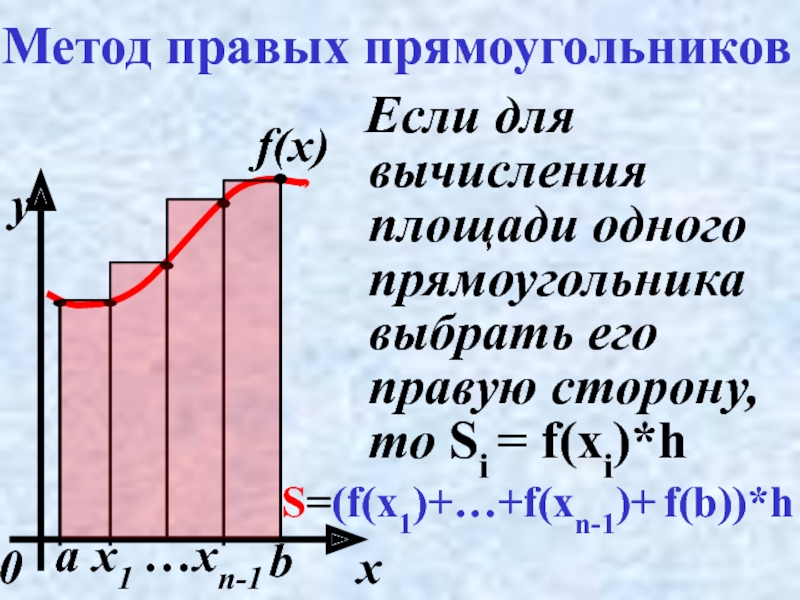
Слайд 15Метод правых прямоугольников
Если для вычисления площади одного прямоугольника выбрать его
x
у
0
f(x)
a
b
S=(f(x1)+…+f(xn-1)+ f(b))*h
x1
xn-1
…
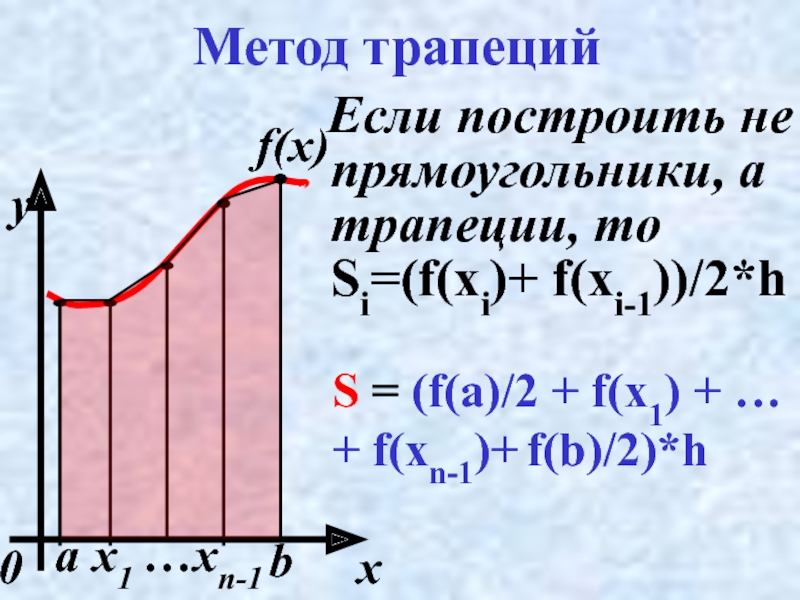
Слайд 16Метод трапеций
Если построить не прямоугольники, а трапеции, то
x
у
0
f(x)
a
b
S = (f(a)/2 + f(x1) + …
+ f(xn-1)+ f(b)/2)*h
x1
xn-1
…
Слайд 18Остроумный метод приближенного вычисления площадей сложных фигур – метод Монте-Карло –
И как это ни парадоксально, но совершенно случайное помогает в вычислении строго определённого.
Слайд 19Дана фигура сложной формы.
Требуется: вычислить площадь этой фигуры.
Суть метода: поместим фигуру
Будем наугад, т. е. случайным образом бросать точки в этот квадрат.
x
у
0
a
a
Слайд 20 Таким образом, при большом числе точек доля точек, содержащихся в фигуре,
M – кол-во точек в фигуре,
N – кол-во точек в квадрате






![Уточнение корней методом половинного деления Пусть f(x) определена на [а,b], непрерывна и f(а)∙ f(b) <](/img/tmb/5/488017/8d85ef4bdec33414399429bff78069c7-800x.jpg)
![Метод построен на вычислении середины отрезка с=(а+b)/2 и выборе из отрезков [а,b] и [с,b]](/img/tmb/5/488017/6e3ac7bf45948a0704360d785f2189b8-800x.jpg)

![Определённый интеграл Можно трактовать как площадь подынтегральной функции (криволинейной трапеции) на отрезке [a;b]xу0f(x)ab= S](/img/tmb/5/488017/c57cb5e51bc0da7dd9f0659143b1be0b-800x.jpg)

![Пусть функция f(x) определена на отрезке [а;b].Требуется: приближенно вычислить определённый интеграл](/img/tmb/5/488017/86d5de1e326ab2d6c13dd4d0f2b649ec-800x.jpg)