- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Изучение вопросов измерения геометрических фигур (на примере темы Площадь многоугольника) презентация
Содержание
- 1. Изучение вопросов измерения геометрических фигур (на примере темы Площадь многоугольника)
- 2. Вопросы: Какие геометрические величины вы знаете?
- 3. План: Геометрические величины и идея их измерения
- 4. Основная литература: Федеральный Государственный образовательный стандарт общего
- 5. Основная литература: Атанасян Л.С. и др. Геометрия
- 6. 1. Геометрические величины и идея их
- 7. Основные сведения о геометрических величинах (продолжение) Каждая
- 8. Этапы рассмотрения измерения геометрических величин в основной
- 9. В старшей школе Расширяются представления о множестве,
- 10. 2. Введение понятия «площадь многоугольника» в 8
- 11. Свойства площади многоугольника Равные многоугольники имеют равные
- 12. Равносоставленные и равновеликие многоугольники Равносоставленные ‒ те,
- 13. Если сторона квадрата равна а, то площадь
- 14. а ‒ конечная десятичная дробь, содержащая n
- 15. а ‒ бесконечная десятичная дробь обозначим аn
- 16. 3. Методические особенности изучения площадей частных
- 17. Приемы введения (доказательства) формул для нахождения площадей
- 18. Параллелограмм, треугольник, трапеция Достраивают до (разбивают на)
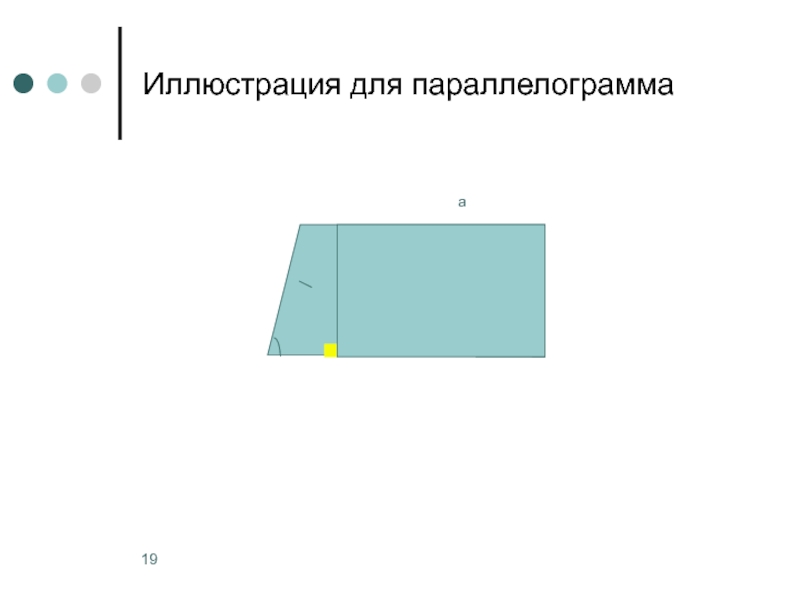
- 19. Иллюстрация для параллелограмма а h
- 20. Приемы доказательства площади трапеции
- 21. Особенности задачного материала темы «Площади многоугольников»
- 22. Доказательство равенства площадей двух фигур №447 (Атанасян)
- 23. Вычисление площадей по известным элементам и обратная
- 24. Получение новых фактов о площадях №474 (Атанасян)
- 25. Получение новых фактов о площадях № 478
- 26. Получение новых фактов, где площадь используется как
- 27. Вопросы для самопроверки Правда ли, что площадь
Слайд 1Лекция 10
Изучение вопросов измерения геометрических фигур (на примере темы «Площадь многоугольника»)
Слайд 2Вопросы:
Какие геометрические величины вы знаете?
Что такое длина?
Что такое площадь?
Что значит измерить
Как можно измерить площадь геометрической фигуры?
Слайд 3План:
Геометрические величины и идея их измерения в школьном курсе математики
Введение понятия
Методические особенности изучения площадей частных видов многоугольников
Слайд 4Основная литература:
Федеральный Государственный образовательный стандарт общего образования (Предметная область «Математика», основная
Методика и технологии обучения математике. Курс лекций /Под научн. ред. Н.Л.Стефановой и Н.С.Подходовой‒ М.,Дрофа, 2005. лекция 23.3 (изучение частных видов четырехугольников и их площадей)
Слайд 5Основная литература:
Атанасян Л.С. и др. Геометрия 7‒9 классы. ‒ М., Просвещение,
Александров и др. Геометрия 7‒9 классы. ‒ М., Просвещение, 2001
Смирнова И.М., Смирнов В.А. Геометрия 7‒9 классы. ‒ М., Просвещение, 2002
И.Ф.Шарыгин. Геометрия 7‒9 ‒ М., Дрофа, 1999
Слайд 61. Геометрические величины и идея их измерения в школьном курсе
Геометрические величины ‒ длина, площадь, объем, мера (градусная или радианная) угла.
Каждая из указанных величин задана на определенном множестве геометрических фигур.
Например, длина ‒ на множестве отрезков (прямых или кривых); площадь на множестве частей поверхностей (плоских или нет), ограниченных замкнутыми линиями (ломаными или кривыми)
Слайд 7Основные сведения о геометрических величинах (продолжение)
Каждая геометрическая величина ‒ аддитивная функция,
Измерение геометрической величины‒ нахождение ее числового значения через соотнесение с единицей измерения (прямое или косвенное)
Слайд 8Этапы рассмотрения измерения геометрических величин в основной школе
В начальной школе ‒
В основной школе вводятся понятия о соответствующих величинах сначала на определенном множестве объектов.
Например, длина отрезка прямой, площадь многоугольника
Косвенные приемы измерения величин ‒ формулы
Слайд 9В старшей школе
Расширяются представления о множестве, на котором рассматриваются геометрические величины
Вывод. Используется индуктивный путь изложения ‒ от практических приемов измерения к теоретическому их обоснованию
Слайд 102. Введение понятия «площадь многоугольника» в 8 классе (учебник Л.С.Атанасяна)
Площадь многоугольника
Площадь скалярная величина, характеризуется положительным числом
Чтобы найти площадь многоугольника нужно узнать, сколько раз единичный квадрат «укладывается» в ограниченной им части плоскости
Единичные квадраты ‒ квадратный сантиметр, квадратный метр, квадратный миллиметр
Слайд 11Свойства площади многоугольника
Равные многоугольники имеют равные площади
Если многоугольник составлен из нескольких
Площадь квадрата равна квадрату его стороны
Слайд 12Равносоставленные и равновеликие многоугольники
Равносоставленные ‒ те, которые разбиваются на одинаковое число
Равновеликие ‒ имеющие равные площади
S1
S1
s2
s2
Слайд 13Если сторона квадрата равна а, то площадь квадрата равна а2.
Пусть а
1
Разделим единичный квадрат на n2 квадратов.
S = = =а2
Слайд 14а ‒ конечная десятичная дробь, содержащая n знаков после запятой
m =
Разделим квадрат со стороной а ‒ на m2 равных квадратов
сторона маленького кв.
Слайд 15а ‒ бесконечная десятичная дробь
обозначим аn ‒ число, полученное из а
8,234|17… 8,234
(8,23417…)‒ 8,234 =(0,00017…)≤ 0,001
аn ≤a ≤an+
(аn )2≤a2 ≤(an+ )2 и (аn )2≤S ≤ (an+ )2
Слайд 163. Методические особенности изучения площадей частных видов многоугольников
Последовательность:
→параллелограмм→треугольник
→трапеция
Слайд 17Приемы введения (доказательства) формул для нахождения площадей
Квадрат ‒ полная индукция
Прямоугольник ‒
(а+b)2 = 2S +a2 + b2
ab = S
а
b
Слайд 18Параллелограмм, треугольник, трапеция
Достраивают до (разбивают на) ранее рассмотренной фигуры
Устанавливают факт равносоставленности
Используют свойство о том, что равносоставленные фигуры имеют равные площади (равновелики)
Слайд 21Особенности задачного материала темы
«Площади многоугольников»
Виды задач:
Доказательство равенства площадей двух фигур
Вычисление
Получение новых фактов о площадях
Получение новых фактов, где площадь используется как посредник
Слайд 22Доказательство равенства площадей двух фигур
№447 (Атанасян)
М= SС(D)
___________________
SABCD = SAMD
А
В
С
D
M
E
Слайд 23Вычисление площадей по известным элементам и обратная задача
№ 469 (Атанасян)
Стороны
Ответ: 8 см
Слайд 24Получение новых фактов о площадях
№474 (Атанасян)
Сравните площади двух треугольников, на которые
№475 (Атанасян)
Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющих равные площади.
Слайд 25Получение новых фактов о площадях
№ 478 (Атанасян)
В выпуклом четырехугольнике диагонали взаимно
№ 467 (Атанасян)
Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
Слайд 26Получение новых фактов, где площадь используется как посредник
№27(полезная) (Шарыгин)
Докажите, что сумма
К
Слайд 27Вопросы для самопроверки
Правда ли, что площадь геометрической фигуры есть число положительное?
Площадь
Показать на чертежах несколько различных приемов обоснования (доказательства) формулы для нахождения площади треугольника