- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приближенное решение нелинейных уравнений. Метод хорд презентация
Содержание
- 1. Приближенное решение нелинейных уравнений. Метод хорд
- 2. ПОСТАНОВКА ЗАДАЧИ Дано F(x)=0, где F(x) определена на [a;b] и удовлетворяет следующим условиям: F(x) непрерывна и F(a)F(b)
- 3. СУТЬ МЕТОДА ХОРД 1. Нелинейная функция f(x)
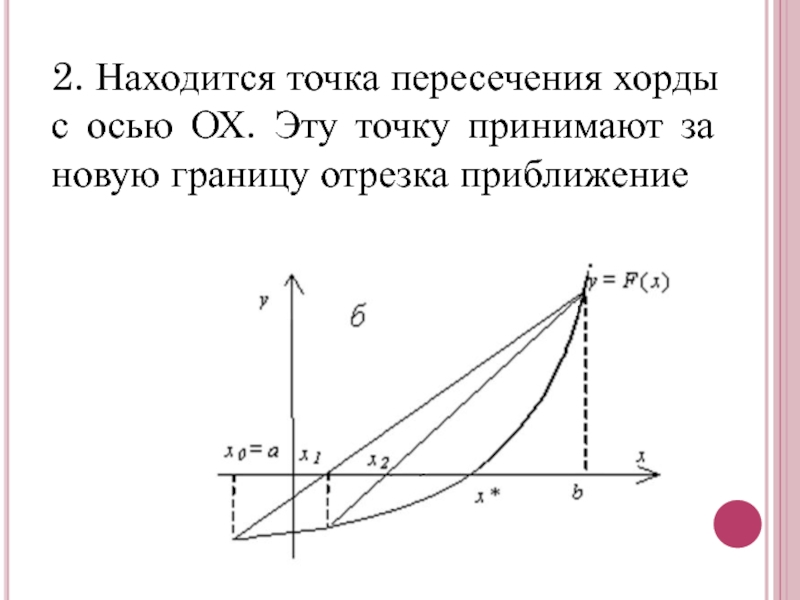
- 4. 2. Находится точка пересечения хорды с осью
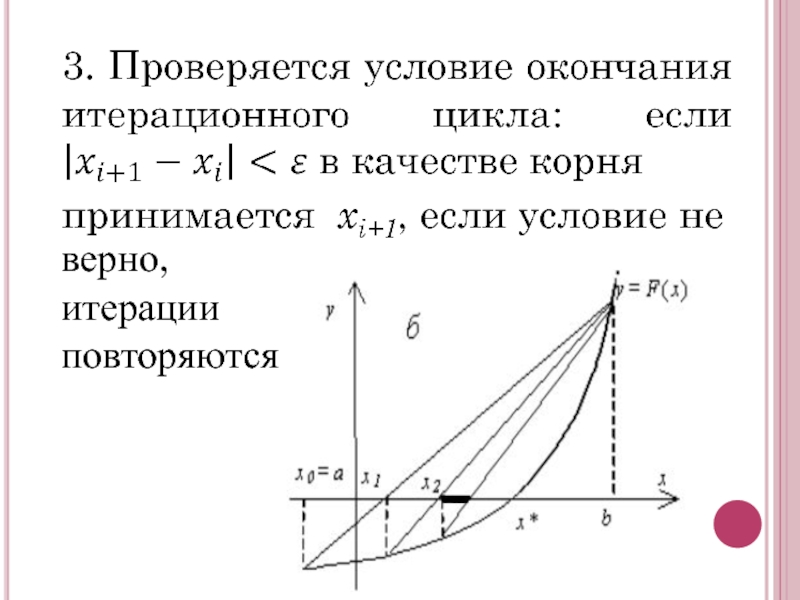
- 5. верно, итерации повторяются
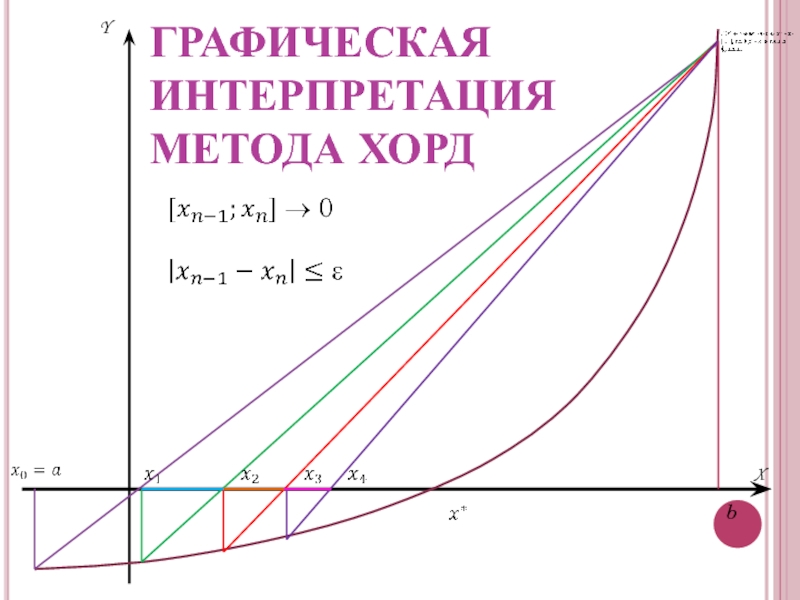
- 6. X Y b
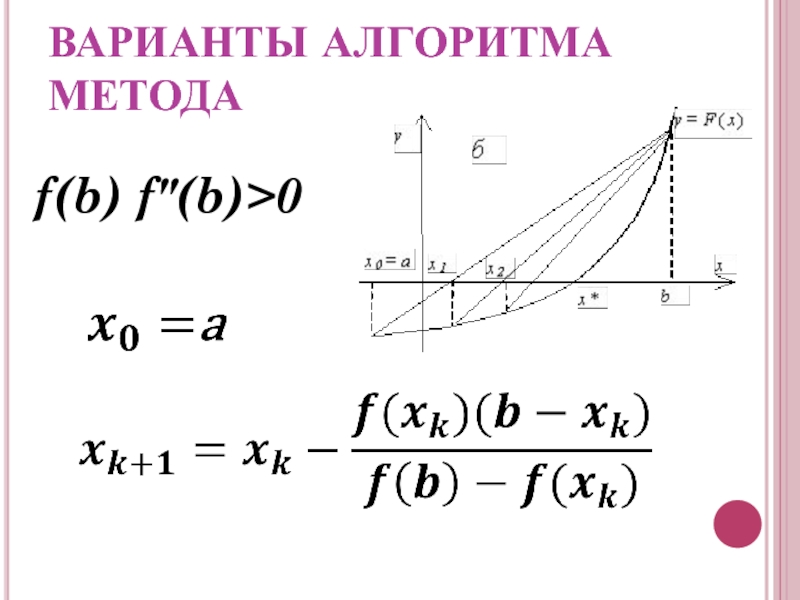
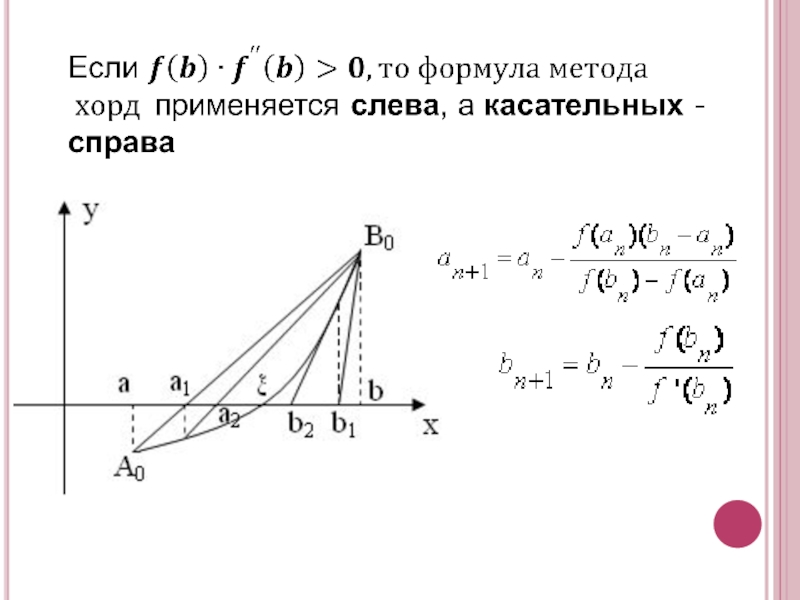
- 7. ВАРИАНТЫ АЛГОРИТМА МЕТОДА f(b) f"(b)>0
- 8.
- 9. РЕШИТЬ УРАВНЕНИЕ
- 10. f(-1) = -1 – 0,2 –
- 11. Для вычислений применяем следующую формулу
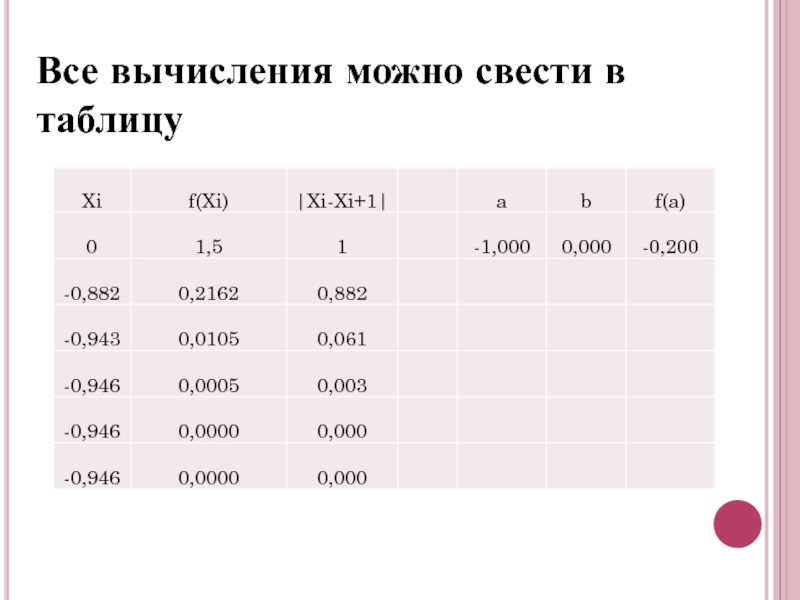
- 12. Все вычисления можно свести в таблицу
- 13. РЕШИТЬ УРАВНЕНИЕ
- 14. f"(х) = 6х f(-2) =
- 15. Для вычислений применяем следующую формулу
- 17. Домашнее задание: решить уравнение методом хорд x3‑ 6x2+3x+11=0
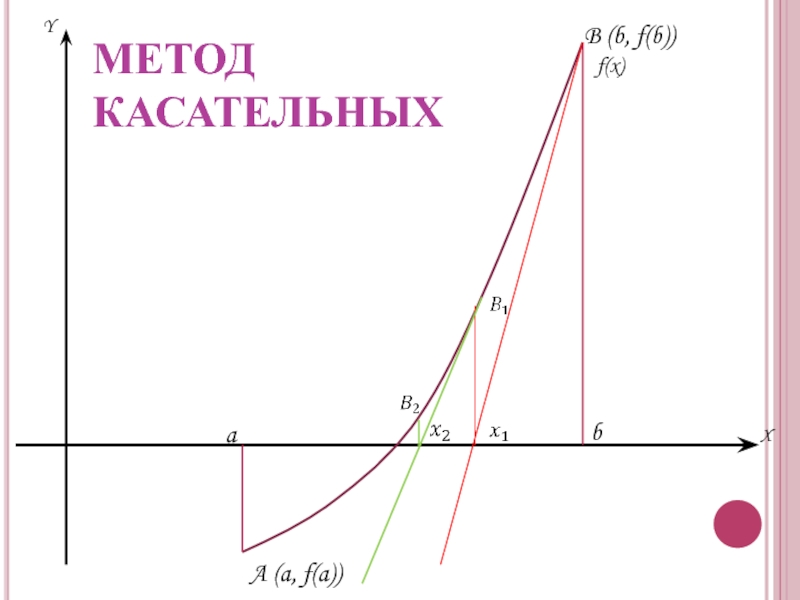
- 18. ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Метод Ньютона (касательных)
- 19. ИДЕЯ МЕТОДА аналогична той, которая реализована
- 20. Выбор начальной точки зависит от свойств функции:
- 21. Очередное приближение вычисляется по формуле:
- 22. Y X B (b, f(b)) A
- 23. ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Комбинирован-ный метод
- 24.
- 25.
- 26.
- 27. Пример Дано уравнение: x3 – 2х2 – 4х +
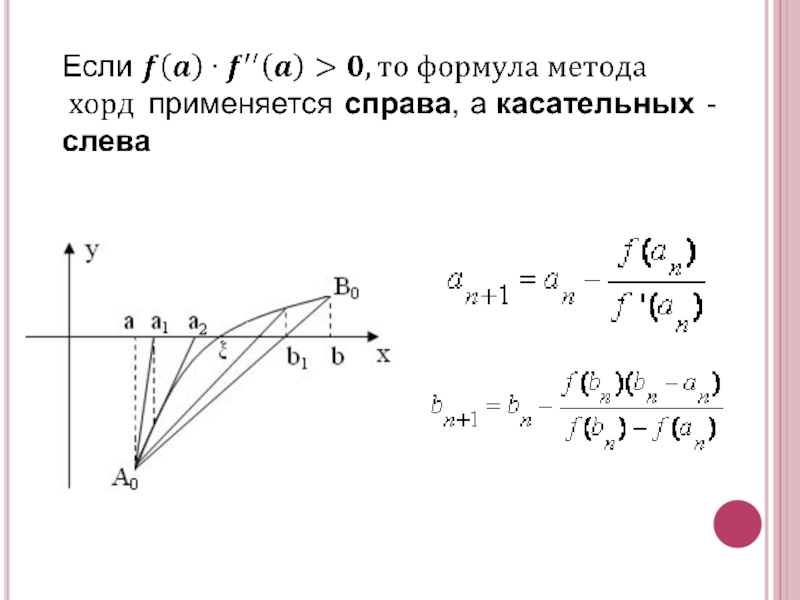
- 28. Вывод: условие выполняется для левой стороны отрезка,
- 29. Корень=-1,91
Слайд 2ПОСТАНОВКА ЗАДАЧИ
Дано F(x)=0, где F(x) определена на [a;b] и удовлетворяет следующим условиям:
F(x)
Необходимое условие существования корня на отрезке [a,b]
Достаточное условие единственности корня
Слайд 3СУТЬ МЕТОДА ХОРД
1. Нелинейная функция f(x) на отделенном отрезке заменяется прямой
стягивающей
точки
(a, f(a))
и (b, f(b)).
Слайд 42. Находится точка пересечения хорды с осью ОХ. Эту точку принимают
Слайд 10
f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2
f(0) = 1,5 > 0.
f"(х) = 6х – 0,4
f"(-1) = -6 – 0,4 = -6,4 < 0;
f"(0) = -0,4 = -0,4 < 0.
Слайд 19ИДЕЯ МЕТОДА
аналогична той, которая реализована в методе хорд, только в качестве
Метод применим к выпуклым и монотонным функциям
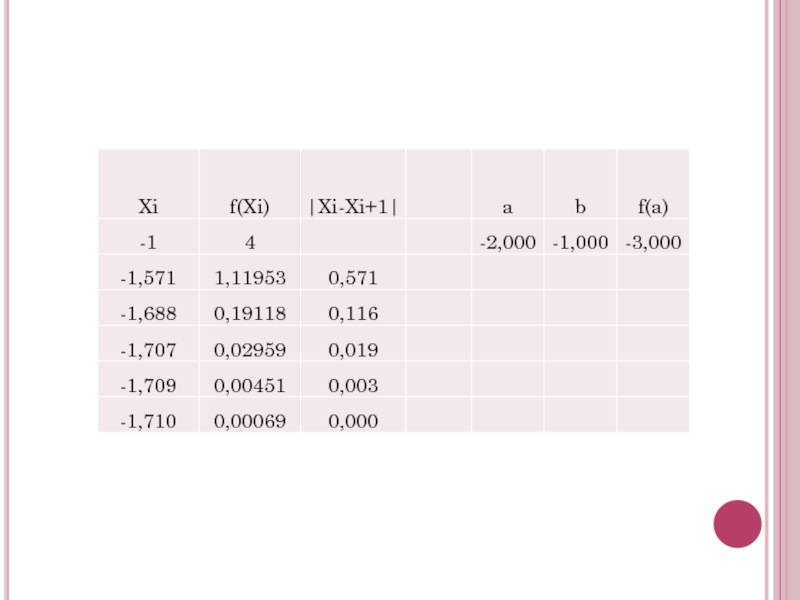
Слайд 27Пример
Дано уравнение: x3 – 2х2 – 4х + 7 = 0.
Найти корень на
Решение:
Проверим условие
f"(х) = 6х – 4
f'(х) = 3х2 – 4x – 4
f(-2) =-1;
f(-1)=8
f"(-2) =-16
f"(-1) =-10

![ПОСТАНОВКА ЗАДАЧИ Дано F(x)=0, где F(x) определена на [a;b] и удовлетворяет следующим условиям:F(x) непрерывна и F(a)F(b)](/img/tmb/3/296823/e7003fe4a45d49007321192bd9615450-800x.jpg)

 0 " alt="">
0 " alt="">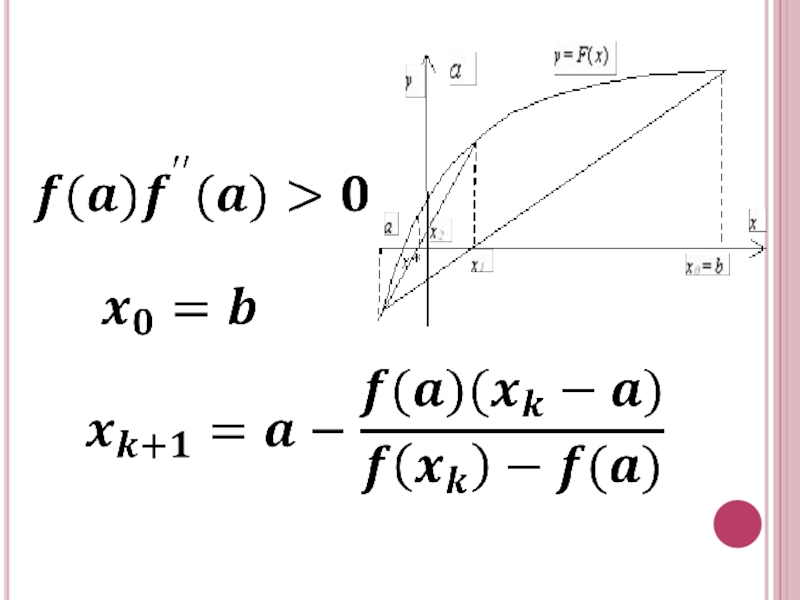

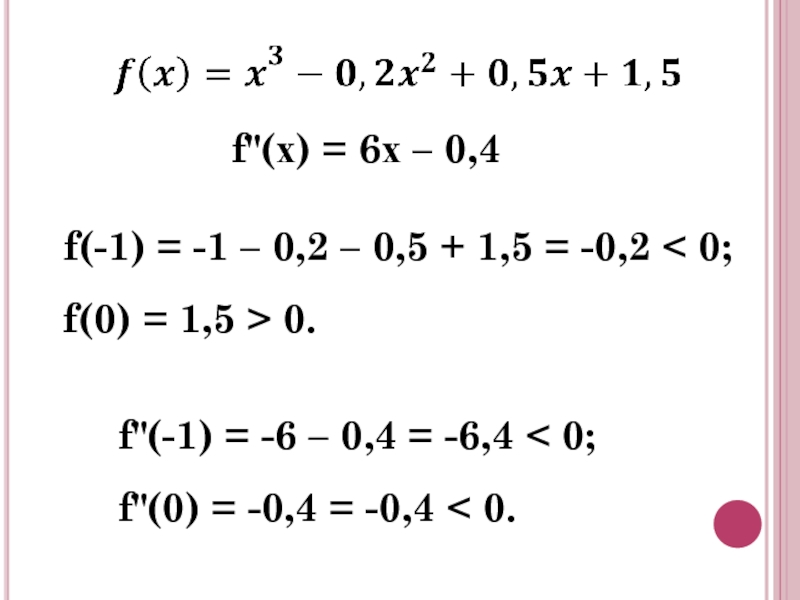


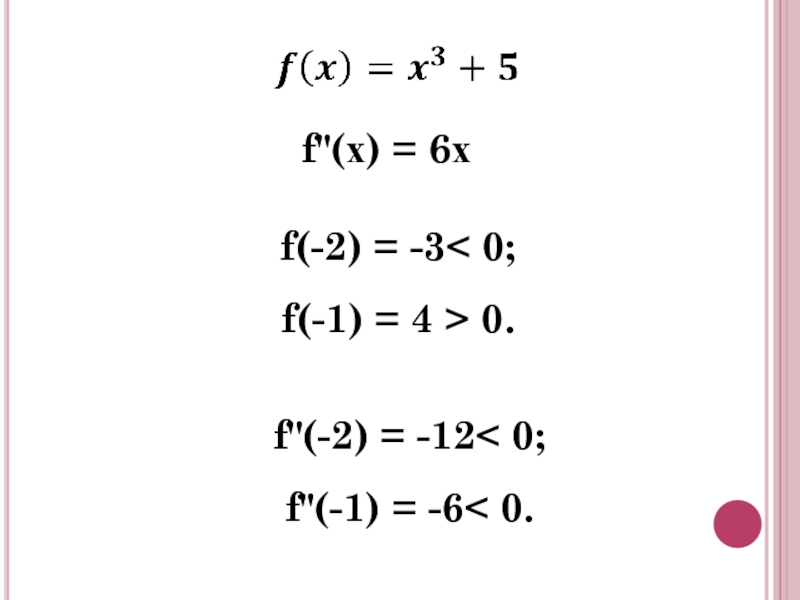 0.f"(-2) = -12< 0;f"(-1) =" alt="">
0.f"(-2) = -12< 0;f"(-1) =" alt="">







![ПримерДано уравнение: x3 – 2х2 – 4х + 7 = 0.Найти корень на отрезке [-2;-1]с погрешностью e < 0,1Решение:Проверим](/img/tmb/3/296823/a0115cb5a1641bfd9d6494f671305d89-800x.jpg)







