Преобразование графиков функций презентация

Содержание

1. Преобразование графиков функций
2. Оглавление Правила преобразований графиков функций Графические
3. Построение графика функции Построение графика функции
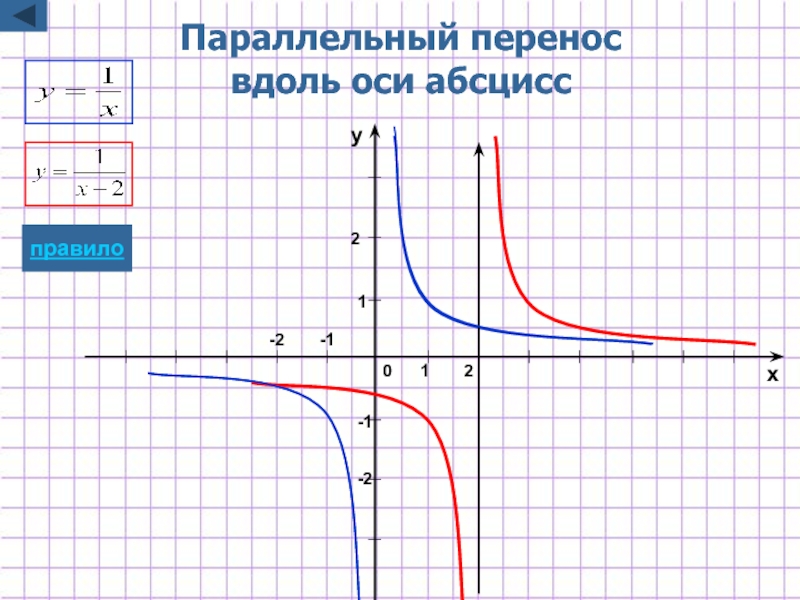
4. Параллельный перенос вдоль оси абсцисс
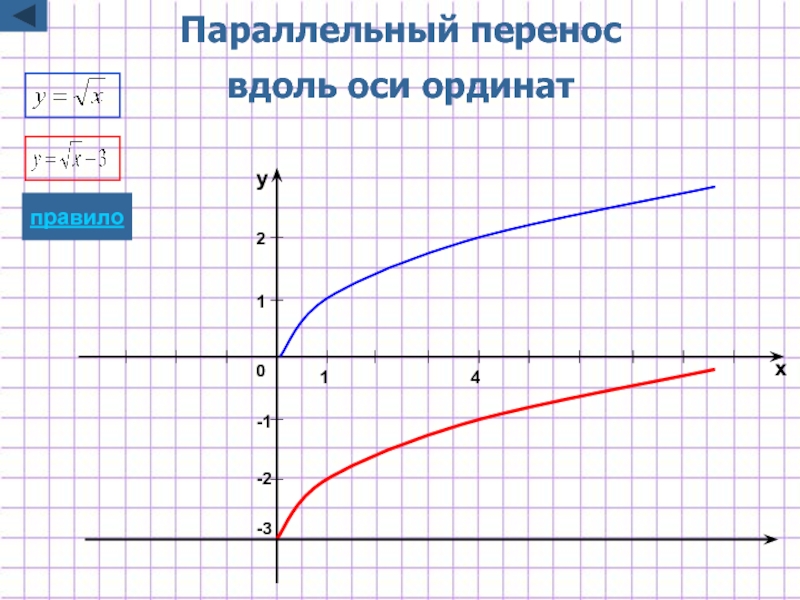
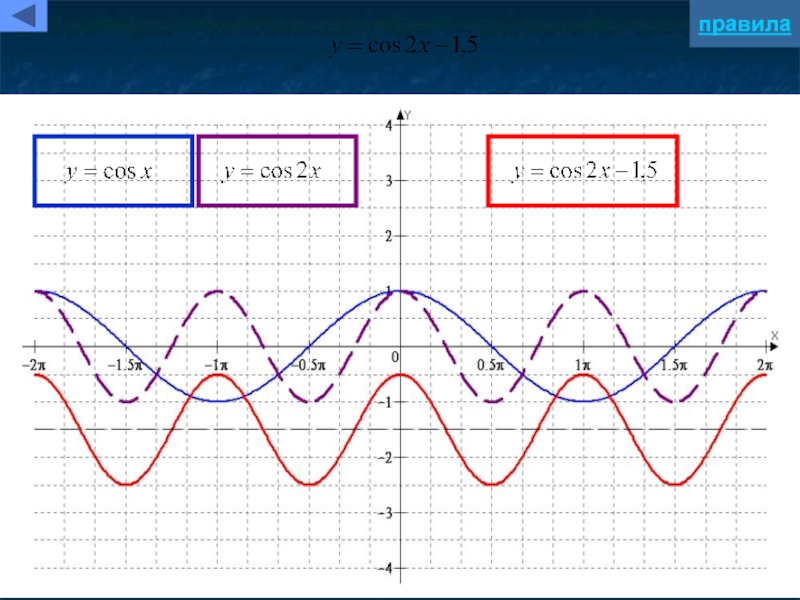
5. Параллельный перенос вдоль оси ординат
6. Симметричное отображение относительно оси ординат
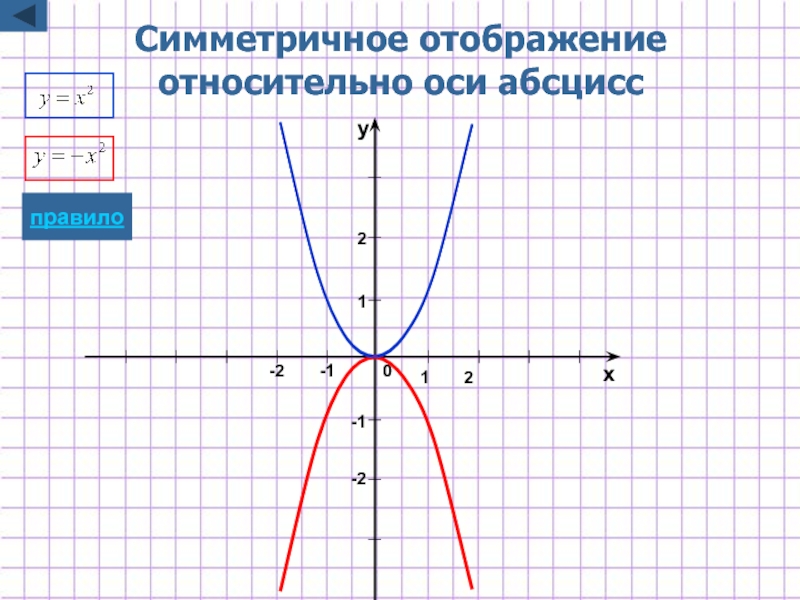
7. Симметричное отображение относительно оси абсцисс
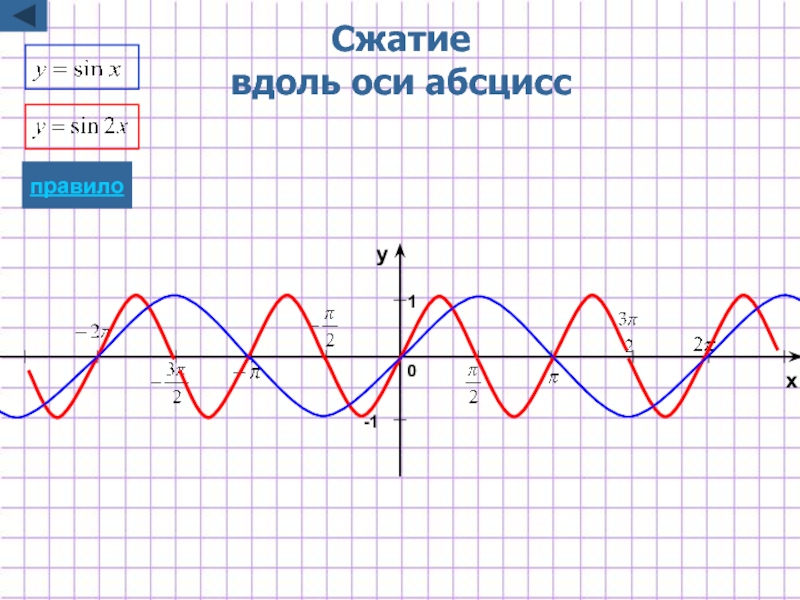
8. Растяжение/сжатие вдоль оси абсцисс y=f(kx)
9. Растяжение/сжатие вдоль оси ординат y=kf(x)
10. Построение графика y=f(|x|) y=f(|x|) Для
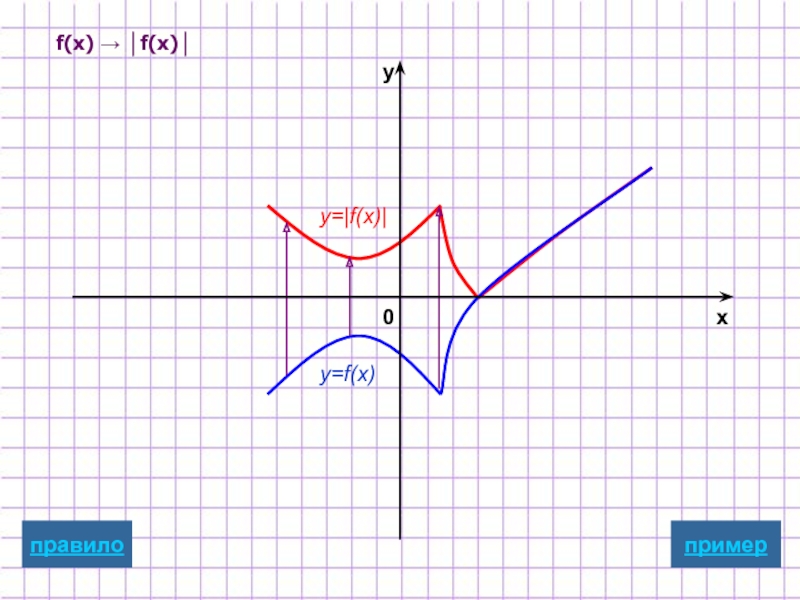
11. Построение графика y=|f(x)| y=|f(x)| Для
12. Графические иллюстрации Построение графика функции Построение графика
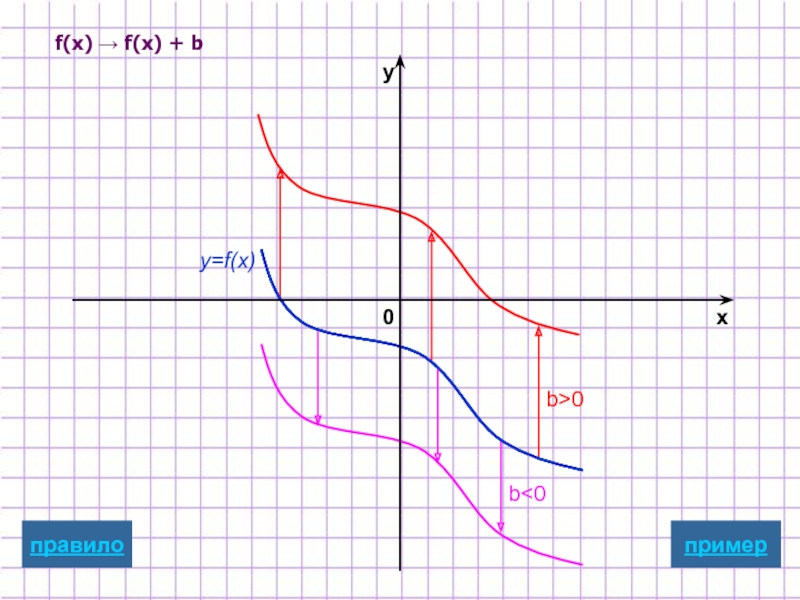
13. f(x) → f(x) + b b>0 b
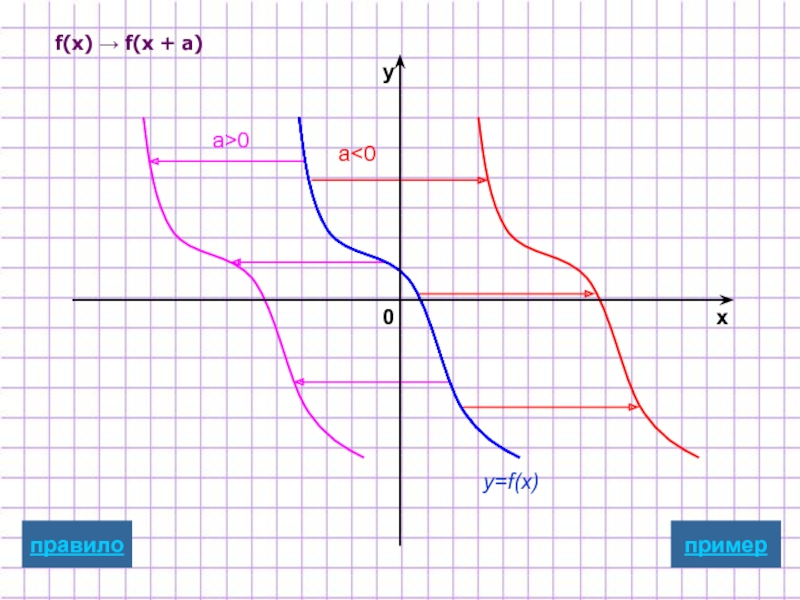
14. f(x) → f(x + а)
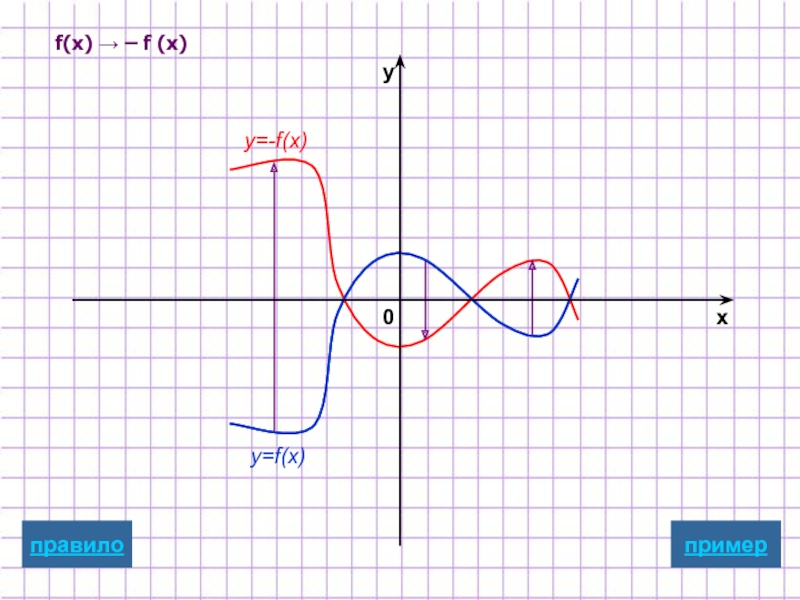
15. f(x) → – f (x)
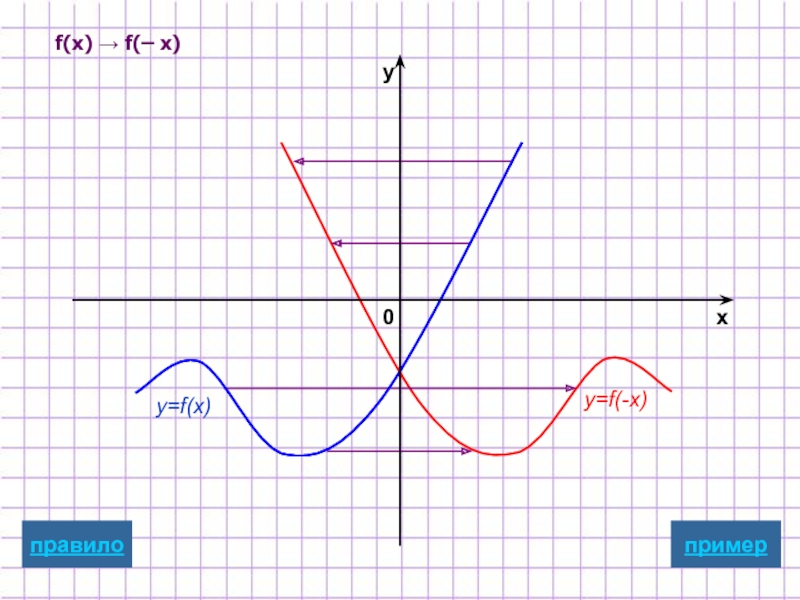
16. f(x) → f(– x) y=f(x) y=f(-x) пример x y 0 правило
17. y=f(x) y=kf(x) пример x
18. y=f(x) y=kf(x) пример x y 0 f(x) → k f(x ) ; 0
19. f(x) → f(kx ) ; k>1
20. f(x) → f(kx ) ; 0
21. f(x) → │f(x)│ y=f(x) y=|f(x)| пример x y 0 правило
22. y=f(x) y=f(|x|) пример x y 0 f(x) → f(|x|) правило
23. Примеры построения графиков сложных функций Построение графика
24. -2 -1 1 2 x y 1
25. -2 -1 1 2 x y
26. -2 -1 1 2 x y 1
27. -1 1 x y 1 2 0
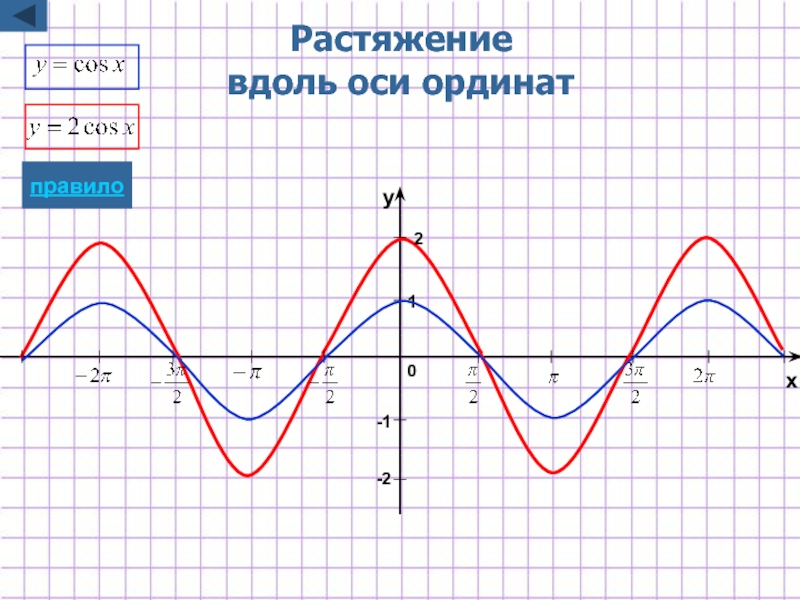
28. Растяжение вдоль оси ординат -2 -1
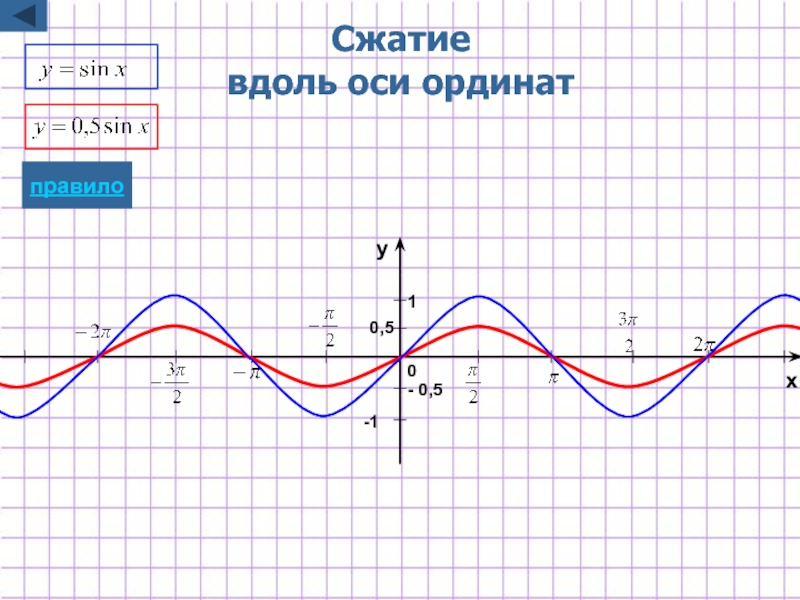
29. Сжатие вдоль оси ординат - 0,5
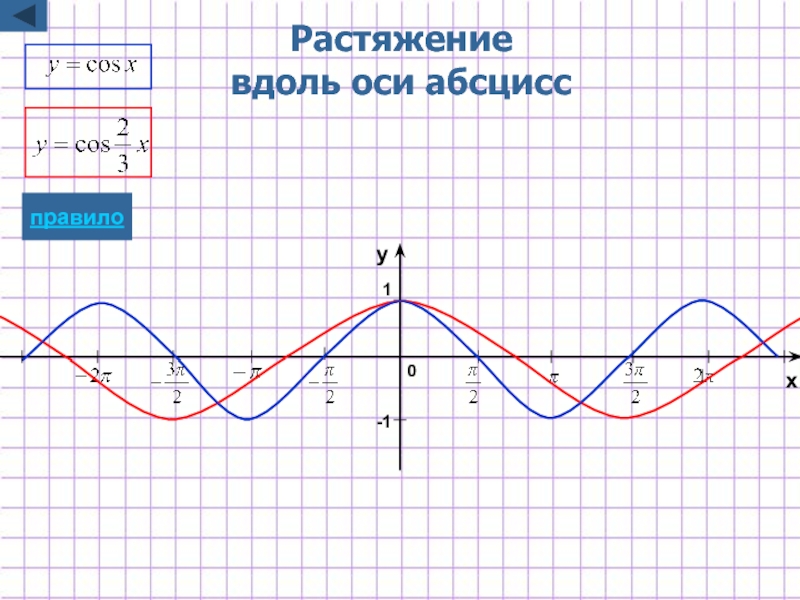
30. Растяжение вдоль оси абсцисс -1 1 x y 0 правило
31. Сжатие вдоль оси абсцисс -1 1 x y 0 правило
32. -1 1 2 x y 1 0
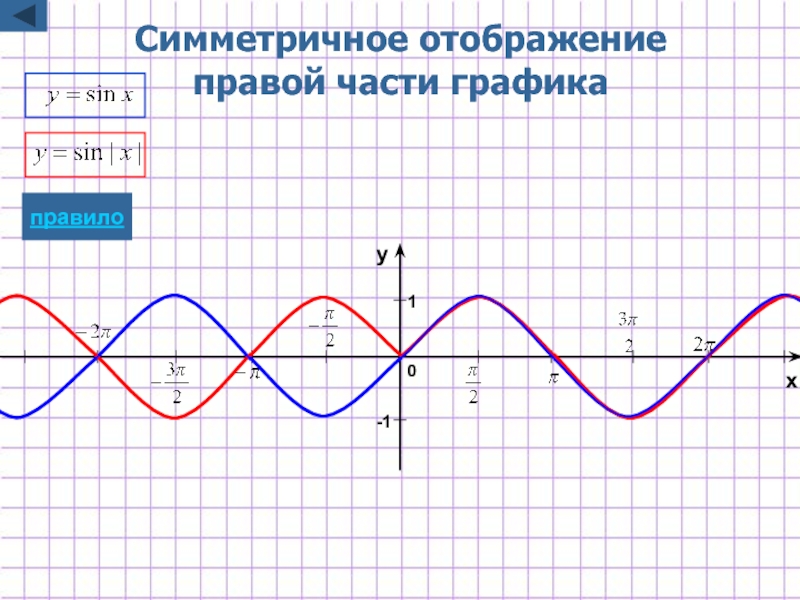
33. Симметричное отображение правой части графика -1 1 x y 0 правило
34. Примеры построения графиков сложных функций оглавление
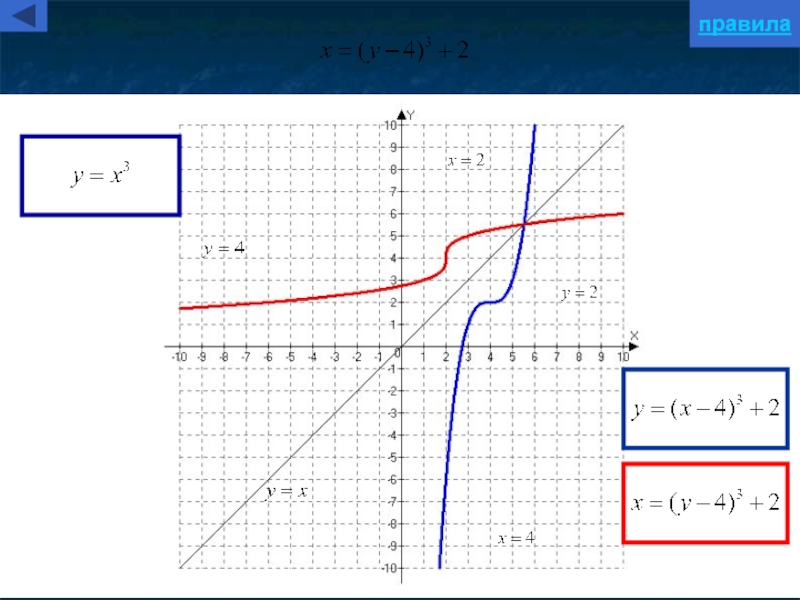
35. правила
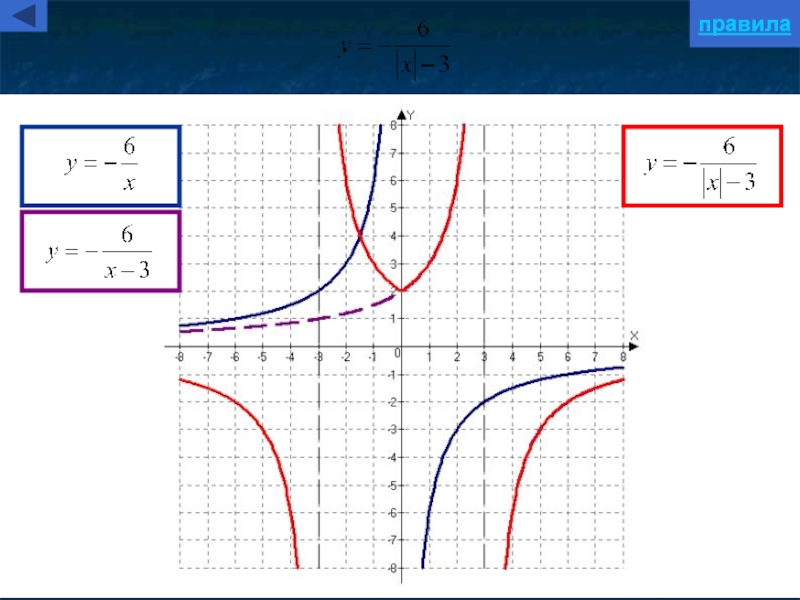
36. правила
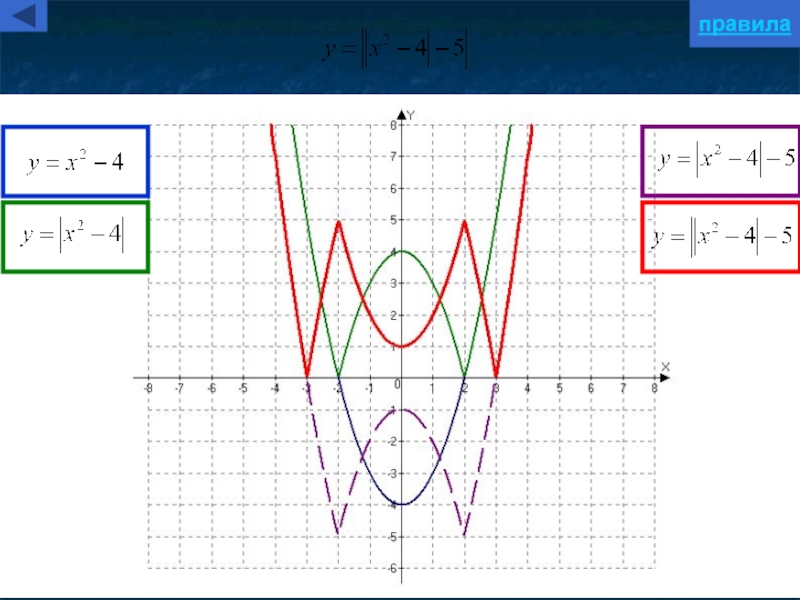
37. правила
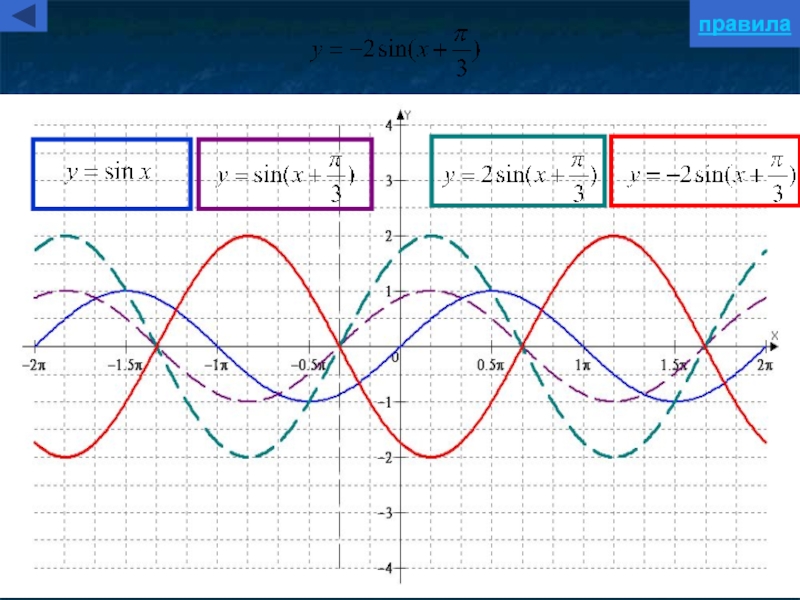
38. правила
39. правила

Главная
Математика
Преобразование графиков функций

Слайд 1Преобразования графиков функций

Слайд 2Оглавление
Правила преобразований графиков функций

Графические иллюстрации

Примеры построения графиков сложных функций с помощью

одного преобразования

Примеры построения графиков сложных функцийПримеры построения графиков сложных функций Примеры построения графиков сложных функций с помощью нескольких преобразований

Слайд 3
Построение графика функции Построение графика функции y=f(x+a)
Построение графика функции Построение графика

функции y=f(x)+b
Построение графика функции Построение графика функции y=f(-x)
Построение графика функции Построение графика функции y=-f(x)
Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx)
Построение графика функции Построение графика функции y=kf(x)
Построение графика функции Построение графика функции y=f(|x|)
Построение графика функции Построение графика функции y=|f(x)|

оглавление

Правила преобразований графиков функций

Слайд 4Параллельный перенос вдоль оси абсцисс
y=f(x+a)

Для построения графика функции y=f(x+a)
надо график

функции y=f(x) параллельно
перенести на |a| единиц вдоль оси Ox
в положительном направлении, если a<0
в отрицательном направлении, если a>0

графическая иллюстрация

Слайд 5Параллельный перенос вдоль оси ординат
y=f(x)+b

Для построения графика функции y=f(x)+b
надо график

функции y=f(x) параллельно
перенести на |b| единиц вдоль оси Oy
в положительном направлении, если b>0
в отрицательном направлении, если b<0

графическая иллюстрация

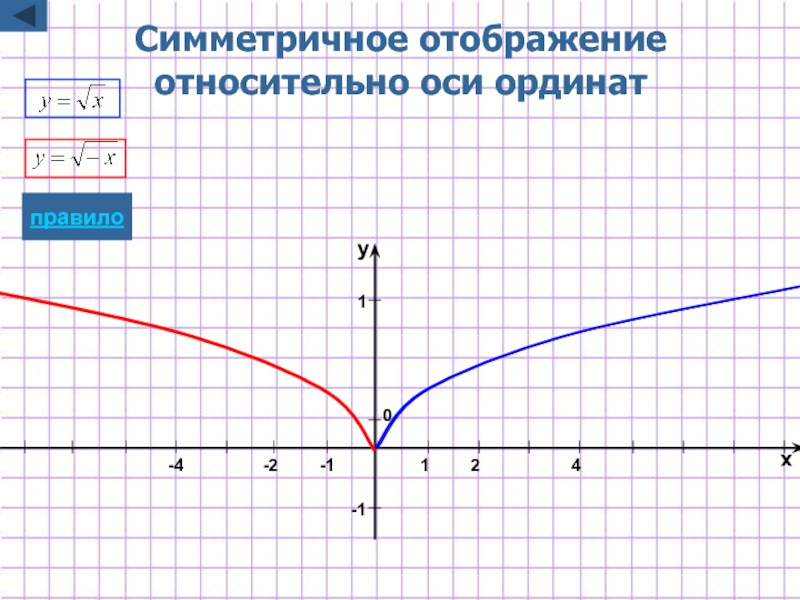
Слайд 6Симметричное отображение относительно оси ординат
y=f(-x)

Для построения графика функции y=f(-x)
надо график

функции y=f(x) симметрично
отобразить относительно оси Oy

Замечание: при этом точки пересечения с осью у остаются неизменными.

графическая иллюстрация

Слайд 7Симметричное отображение относительно оси абсцисс
y=-f(x)

Для построения графика функции y=-f(x)
надо график

функции y=f(x) симметрично
отобразить относительно оси Ox

Замечание: при этом точки пересечения с осью х остаются неизменными.

графическая иллюстрация

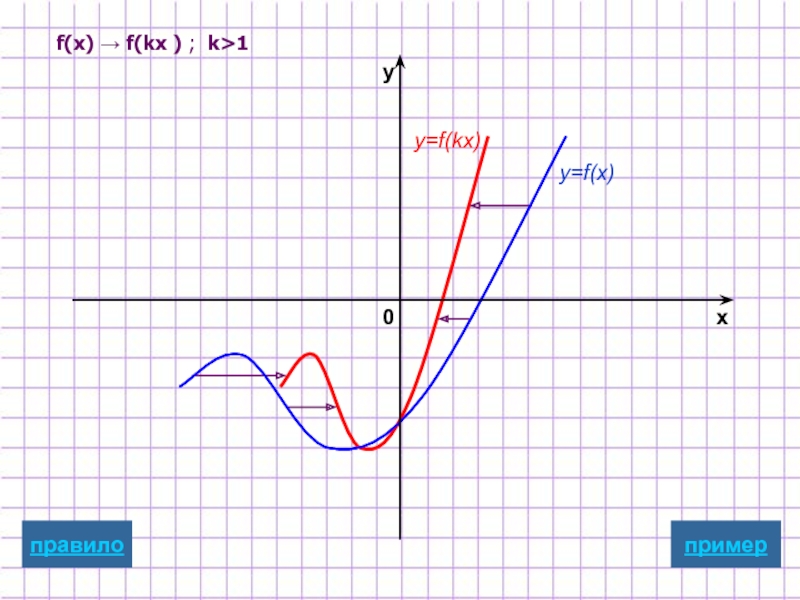
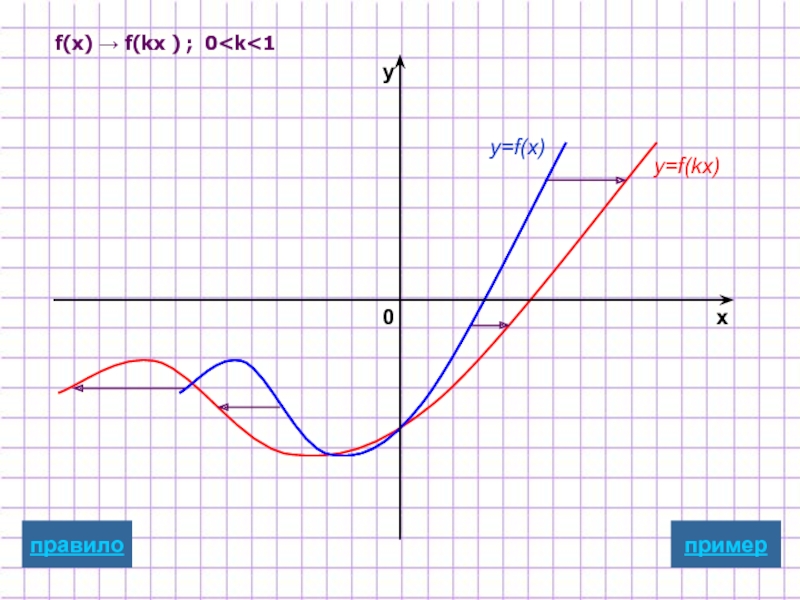
Слайд 8Растяжение/сжатие вдоль оси абсцисс
y=f(kx)
Для построения графика функции y=f(kx)
надо график

функции y=f(x) подвергнуть
масштабированию вдоль оси Ox
растяжению в 1/k раз , если 0сжатию в k раз, если k>1

Замечание: при этом точки пересечения с осью у остаются неизменными.

графическая иллюстрацияграфическая иллюстрация 1

графическая иллюстрацияграфическая иллюстрация 2

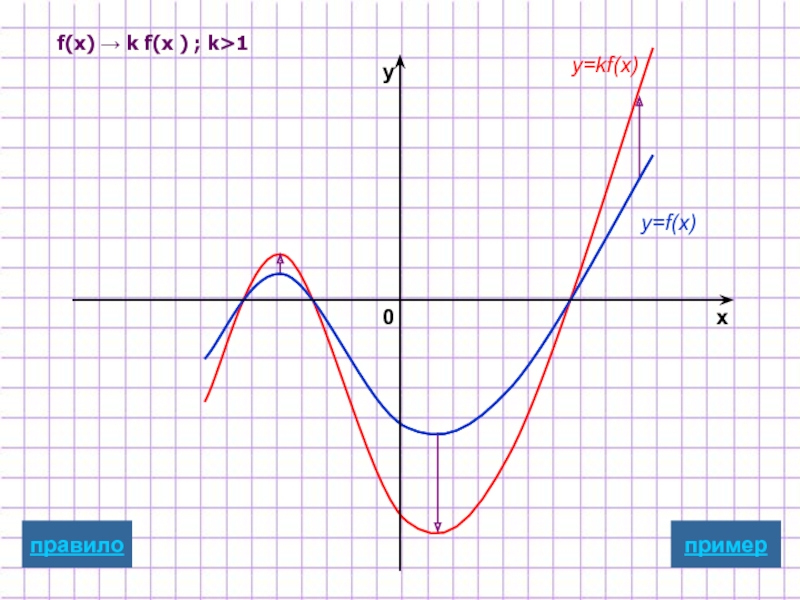
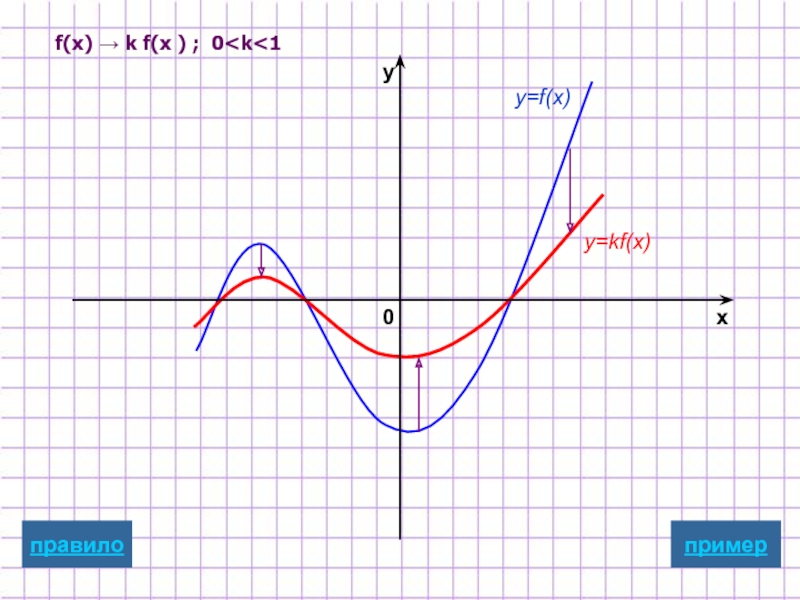
Слайд 9Растяжение/сжатие вдоль оси ординат
y=kf(x)
Для построения графика функции y=kf(x)
надо график

функции y=f(x) подвергнуть
масштабированию вдоль оси Oy
растяжению в k раз , если k>1
сжатию в 1/k раз, если 0
Замечание: при этом точки пересечения с осью х остаются неизменными.

графическая иллюстрация 2

графическая иллюстрация 1

Слайд 10Построение графика y=f(|x|)
y=f(|x|)

Для построения графика функции y=f(|x|) надо:
часть графика

функции y=f(x), лежащую правее оси Oy, оставить без изменения;
эту же часть графика функции y=f(x), лежащую правее оси Oy, симметрично отобразить относительно оси Оy

графическая иллюстрация

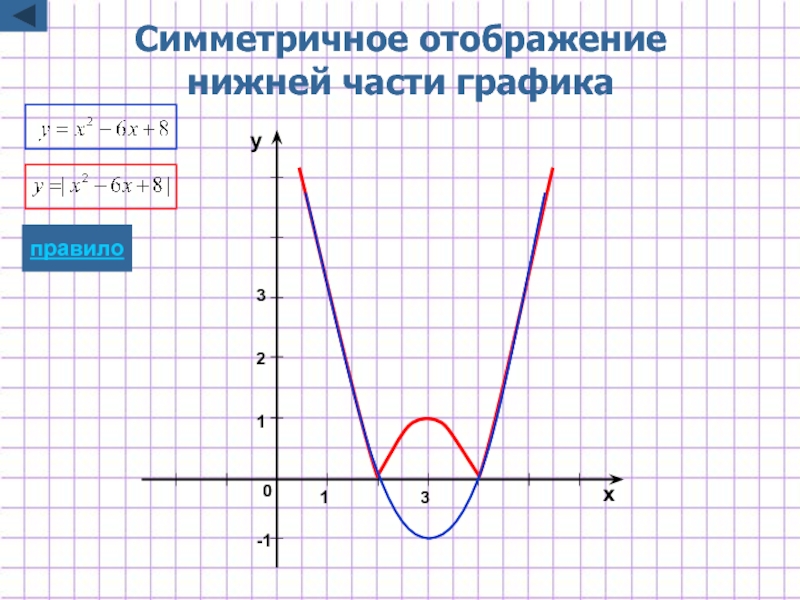
Слайд 11Построение графика y=|f(x)|
y=|f(x)|

Для построения графика функции y=|f(x)| надо:
часть графика

функции y=f(x), лежащую выше оси Oх, оставить без изменения;
часть графика функции y=f(x), лежащую ниже оси Oх, симметрично отобразить относительно оси Ох

графическая иллюстрация

Слайд 12Графические иллюстрации
Построение графика функции Построение графика функции y=f(x+a)
Построение графика функции Построение

графика функции y=f(x)+b
Построение графика функции Построение графика функции y=f(-x)
Построение графика функции Построение графика функции y=-f(x)
Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx), Построение графика функции y=f(kx), 0Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx), Построение графика функции y=f(kx), k>1
Построение графика функции Построение графика функции y=kf(x)Построение графика функции y=kf(x), Построение графика функции y=kf(x), 0Построение графика функции Построение графика функции y=kf(x), k>1
Построение графика функции Построение графика функции y=f(|x|)
Построение графика функции Построение графика функции y=|f(x)|

оглавление

примеры

правила

Слайд 13f(x) → f(x) + b

b>0
b

Слайд 14f(x) → f(x + а)

a0
y=f(x)
пример

x
y
0
правило

Слайд 15f(x) → – f (x)

y=f(x)
y=-f(x)
пример

x
y
0
правило

Слайд 16f(x) → f(– x)

y=f(x)
y=f(-x)
пример

x
y
0
правило

Слайд 17

y=f(x)
y=kf(x)
пример

x
y
0
f(x) → k f(x ) ; k>1
правило

Слайд 18

y=f(x)
y=kf(x)
пример
x
y
0
f(x) → k f(x ) ; 0

Слайд 19f(x) → f(kx ) ; k>1

y=f(x)
y=f(kx)
пример

x
y
0
правило

Слайд 20f(x) → f(kx ) ; 0

Слайд 21f(x) → │f(x)│
y=f(x)
y=|f(x)|
пример
x
y
0
правило

Слайд 22y=f(x)
y=f(|x|)
пример
x
y
0
f(x) → f(|x|)
правило

Слайд 23Примеры построения графиков сложных функций
Построение графика функции Построение графика функции y=f(x+a)
Построение

графика функции Построение графика функции y=f(x)+b
Построение графика функции Построение графика функции y=f(-x)
Построение графика функции Построение графика функции y=-f(x)
Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx), Построение графика функции y=f(kx), 0Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx), Построение графика функции y=f(kx), k>1
Построение графика функции Построение графика функции y=kf(x)Построение графика функции y=kf(x), Построение графика функции y=kf(x), 0Построение графика функции Построение графика функции y=kf(x), k>1
Построение графика функции Построение графика функции y=f(|x|)
Построение графика функции Построение графика функции y=|f(x)|

оглавление

Слайд 24-2
-1
1
2
x
y
1
2
0
Параллельный перенос вдоль оси абсцисс

-1
-2

правило

Слайд 25-2
-1
1
2
x
y

1
4
0

-3
Параллельный перенос вдоль оси ординат

правило

Слайд 26-2
-1
1
2
x
y
1
2
0
Симметричное отображение относительно оси абсцисс
-1
-2

правило

Слайд 27-1
1
x
y
1
2
0
Симметричное отображение относительно оси ординат
-1
-2

4
-4

правило

Слайд 28Растяжение вдоль оси ординат
-2
-1
1
2
x
y

0

правило

Слайд 29Сжатие вдоль оси ординат
- 0,5
-1
1
0,5
x
y

0

правило

Слайд 30Растяжение вдоль оси абсцисс
-1
1
x
y
0

правило

Слайд 31Сжатие вдоль оси абсцисс
-1
1
x
y

0

правило

Слайд 32-1
1
2
x
y
1
0
3

3

Симметричное отображение нижней части графика

правило

Слайд 33Симметричное отображение правой части графика
-1
1
x
y
0

правило

Слайд 34Примеры построения графиков сложных функций

оглавление

Слайд 35

правила

Слайд 36

правила

Слайд 37

правила

Слайд 38

правила

Слайд 39

правила

Слайд 40

Скачать презентацию

Преобразование графиков функций презентация

Содержание

Слайд 1Преобразования графиков функций

Слайд 2ОглавлениеПравила преобразований графиков функцийГрафические иллюстрацииПримеры построения графиков сложных функций с помощью

Слайд 3Построение графика функции Построение графика функции y=f(x+a)Построение графика функции Построение графика

Слайд 4Параллельный перенос вдоль оси абсцисс y=f(x+a)Для построения графика функции y=f(x+a)надо график

Слайд 5Параллельный перенос вдоль оси ординат y=f(x)+bДля построения графика функции y=f(x)+bнадо график

Слайд 6Симметричное отображение относительно оси ординат y=f(-x)Для построения графика функции y=f(-x)надо график

Слайд 7Симметричное отображение относительно оси абсцисс y=-f(x)Для построения графика функции y=-f(x)надо график

Слайд 8Растяжение/сжатие вдоль оси абсцисс y=f(kx)Для построения графика функции y=f(kx) надо график

Слайд 9Растяжение/сжатие вдоль оси ординат y=kf(x)Для построения графика функции y=kf(x) надо график

Слайд 10Построение графика y=f(|x|) y=f(|x|)Для построения графика функции y=f(|x|) надо: часть графика

Слайд 11Построение графика y=|f(x)| y=|f(x)|Для построения графика функции y=|f(x)| надо: часть графика

Слайд 12Графические иллюстрацииПостроение графика функции Построение графика функции y=f(x+a)Построение графика функции Построение

Слайд 13f(x) → f(x) + b b>0b

Слайд 14f(x) → f(x + а) a0y=f(x)примерxy0правило

Слайд 15f(x) → – f (x) y=f(x)y=-f(x)примерxy0правило

Слайд 16f(x) → f(– x) y=f(x)y=f(-x)примерxy0правило

Слайд 17y=f(x)y=kf(x)примерxy0f(x) → k f(x ) ; k>1правило

Слайд 18y=f(x)y=kf(x)примерxy0f(x) → k f(x ) ; 0

Слайд 19f(x) → f(kx ) ; k>1y=f(x)y=f(kx)примерxy0правило

Слайд 20f(x) → f(kx ) ; 0

Слайд 21f(x) → │f(x)│ y=f(x)y=|f(x)|примерxy0правило

Слайд 22y=f(x)y=f(|x|)примерxy0f(x) → f(|x|)правило

Слайд 23Примеры построения графиков сложных функцийПостроение графика функции Построение графика функции y=f(x+a)Построение

Слайд 24-2-112xy120Параллельный перенос вдоль оси абсцисс-1-2правило

Слайд 25-2-112xy140-3Параллельный перенос вдоль оси ординат правило

Слайд 26-2-112xy120Симметричное отображение относительно оси абсцисс-1-2правило

Слайд 27-11xy120Симметричное отображение относительно оси ординат-1-24-4правило

Слайд 28Растяжение вдоль оси ординат-2-112xy0правило

Слайд 29Сжатие вдоль оси ординат- 0,5-110,5xy0правило

Слайд 30Растяжение вдоль оси абсцисс-11xy0правило

Слайд 31Сжатие вдоль оси абсцисс-11xy0правило

Слайд 32-112xy1033Симметричное отображение нижней части графикаправило

Слайд 33Симметричное отображение правой части графика-11xy0правило

Слайд 34Примеры построения графиков сложных функцийоглавление

Слайд 35правила

Слайд 36правила

Слайд 37правила

Слайд 38правила

Слайд 39правила

Слайд 40

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2Оглавление
Правила преобразований графиков функций

Графические иллюстрации

Примеры построения графиков сложных функций с помощью

Слайд 3
Построение графика функции Построение графика функции y=f(x+a)
Построение графика функции Построение графика

Слайд 4Параллельный перенос вдоль оси абсцисс
y=f(x+a)

Для построения графика функции y=f(x+a)
надо график

Слайд 5Параллельный перенос вдоль оси ординат
y=f(x)+b

Для построения графика функции y=f(x)+b
надо график

Слайд 6Симметричное отображение относительно оси ординат
y=f(-x)

Для построения графика функции y=f(-x)
надо график

Слайд 7Симметричное отображение относительно оси абсцисс
y=-f(x)

Для построения графика функции y=-f(x)
надо график

Слайд 8Растяжение/сжатие вдоль оси абсцисс
y=f(kx)
Для построения графика функции y=f(kx)
надо график

Слайд 9Растяжение/сжатие вдоль оси ординат
y=kf(x)
Для построения графика функции y=kf(x)
надо график

Слайд 10Построение графика y=f(|x|)
y=f(|x|)

Для построения графика функции y=f(|x|) надо:
часть графика

Слайд 11Построение графика y=|f(x)|
y=|f(x)|

Для построения графика функции y=|f(x)| надо:
часть графика

Слайд 12Графические иллюстрации
Построение графика функции Построение графика функции y=f(x+a)
Построение графика функции Построение

Слайд 13f(x) → f(x) + b

b>0
b

Слайд 14f(x) → f(x + а)

a0
y=f(x)
пример

x
y
0
правило

Слайд 15f(x) → – f (x)

y=f(x)
y=-f(x)
пример

x
y
0
правило

Слайд 16f(x) → f(– x)

y=f(x)
y=f(-x)
пример

x
y
0
правило

Слайд 17

y=f(x)
y=kf(x)
пример

x
y
0
f(x) → k f(x ) ; k>1
правило

Слайд 18

y=f(x)
y=kf(x)
пример
x
y
0
f(x) → k f(x ) ; 0

Слайд 19f(x) → f(kx ) ; k>1

y=f(x)
y=f(kx)
пример

x
y
0
правило

Слайд 21f(x) → │f(x)│
y=f(x)
y=|f(x)|
пример
x
y
0
правило

Слайд 22y=f(x)
y=f(|x|)
пример
x
y
0
f(x) → f(|x|)
правило

Слайд 23Примеры построения графиков сложных функций
Построение графика функции Построение графика функции y=f(x+a)
Построение

Слайд 24-2
-1
1
2
x
y
1
2
0
Параллельный перенос вдоль оси абсцисс

-1
-2

правило

Слайд 25-2
-1
1
2
x
y

1
4
0

-3
Параллельный перенос вдоль оси ординат

правило

Слайд 26-2
-1
1
2
x
y
1
2
0
Симметричное отображение относительно оси абсцисс
-1
-2

правило

Слайд 27-1
1
x
y
1
2
0
Симметричное отображение относительно оси ординат
-1
-2

4
-4

правило

Слайд 28Растяжение вдоль оси ординат
-2
-1
1
2
x
y

0

правило

Слайд 29Сжатие вдоль оси ординат
- 0,5
-1
1
0,5
x
y

0

правило

Слайд 30Растяжение вдоль оси абсцисс
-1
1
x
y
0

правило

Слайд 31Сжатие вдоль оси абсцисс
-1
1
x
y

0

правило

Слайд 32-1
1
2
x
y
1
0
3

3

Симметричное отображение нижней части графика

правило

Слайд 33Симметричное отображение правой части графика
-1
1
x
y
0

правило

Слайд 34Примеры построения графиков сложных функций

оглавление

Слайд 35

правила

Слайд 36

правила

Слайд 37

правила

Слайд 38

правила

Слайд 39

правила