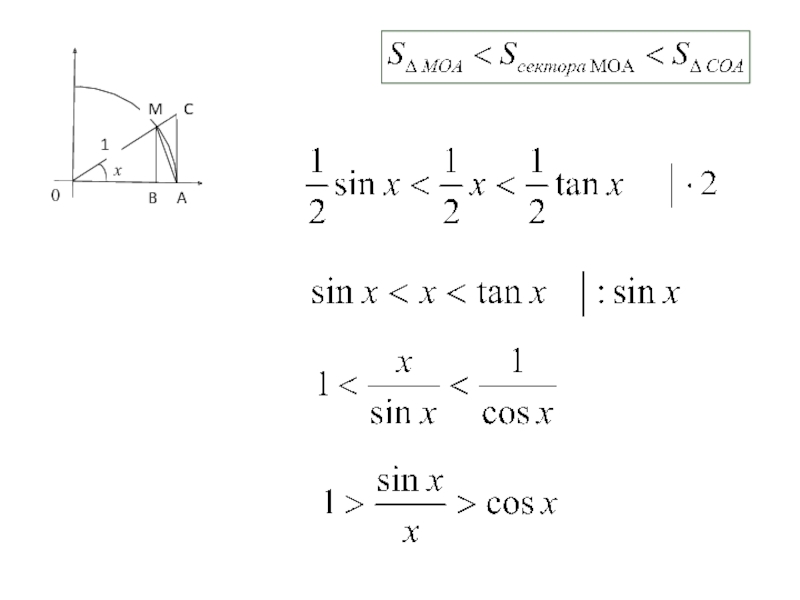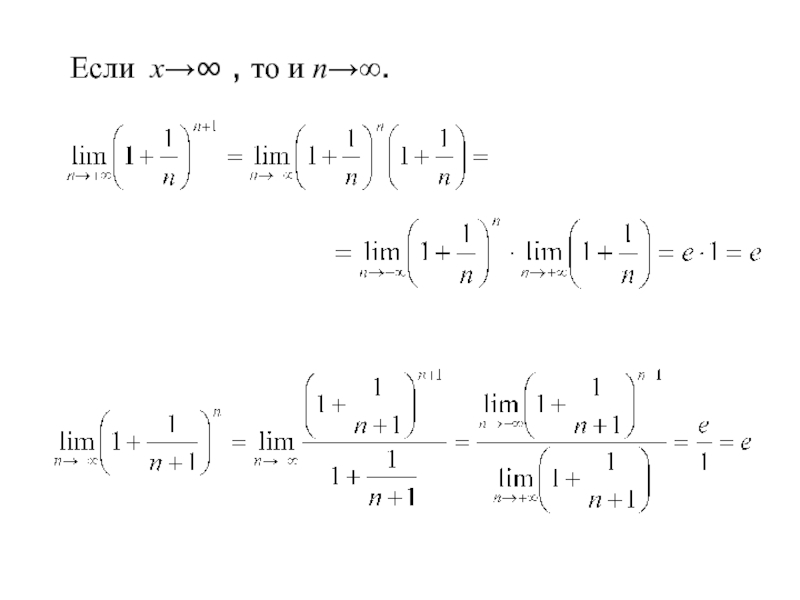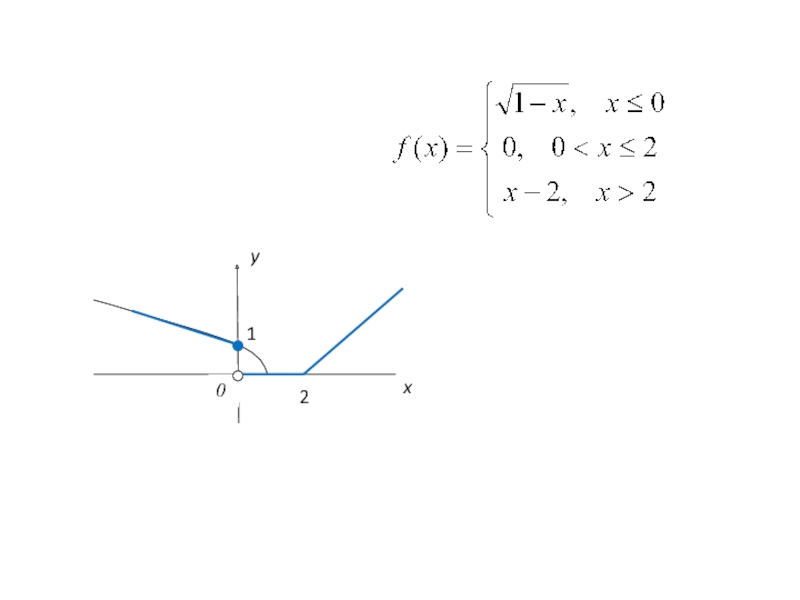- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел и непрерывность функции презентация
Содержание
- 1. Предел и непрерывность функции
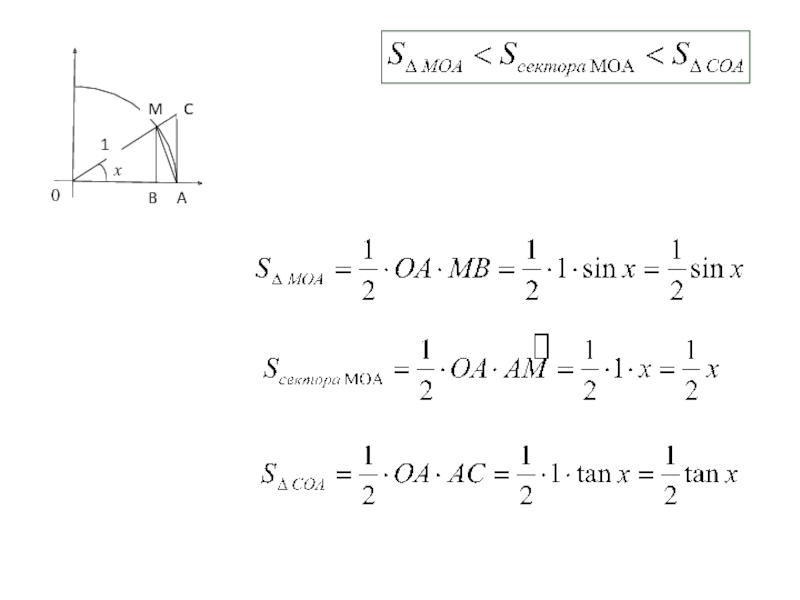
- 2. Замечательные пределы. Доказательство:
- 3. C M
- 4. C M
- 5. C M
- 6. Вычисление пределов функций Вычислить
- 7. Вычисление пределов функций 2) Вычислить
- 8. II. Второй замечательный предел
- 9. Определение.
- 11. Доказательство: 1) пусть х→+∞
- 12. Если х→∞ , то и n→∞.
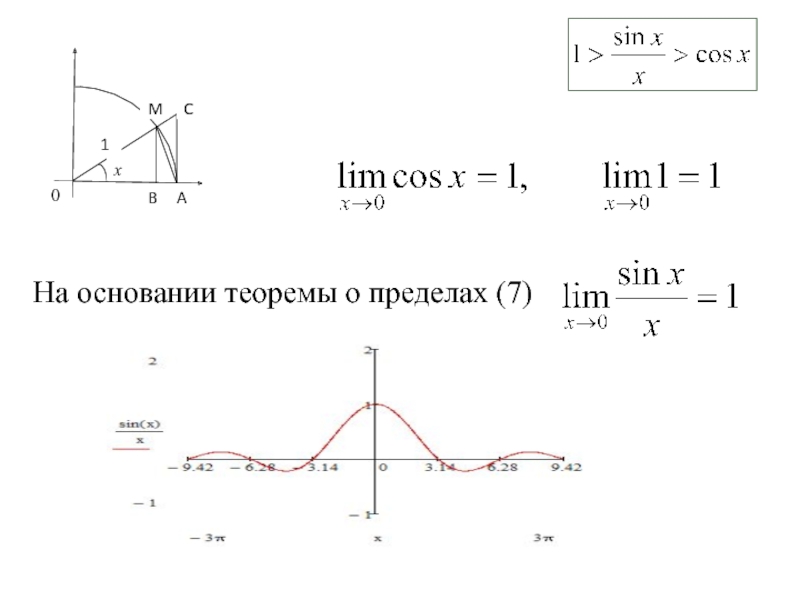
- 13. На основании теоремы о пределах (7):
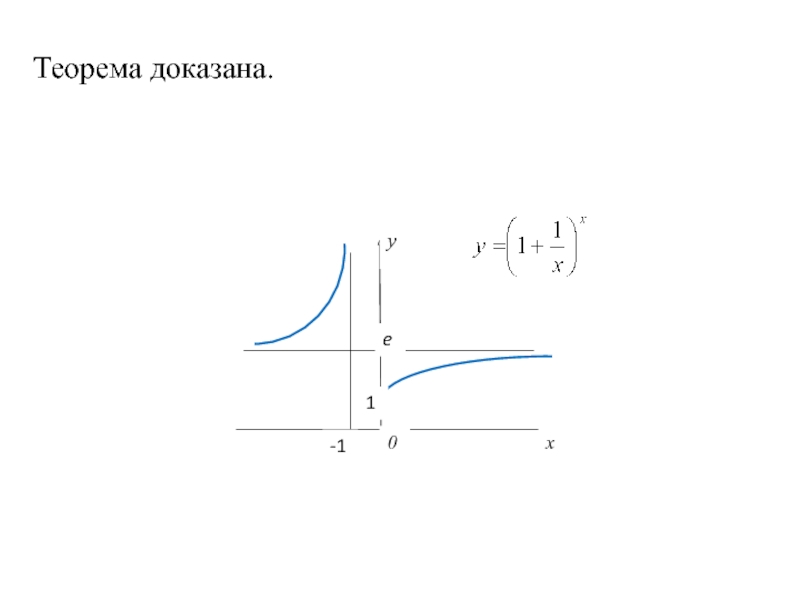
- 14. Теорема доказана.
- 15. Если , то при х→∞ имеем α→0 . Тогда
- 16. Вычисление пределов функций Вычислить
- 17. Вычисление пределов функций Вычислить пусть
- 18. Экспонента (exponential function) механика
- 19. Непрерывность функции. Пример
- 20. Пример 2.
- 21. Определение 1. Функция f(x) называется непрерывной в
- 22. Исследовать данную функцию на непрерывность Для х1=0: Функция f(x) в точке х1=0 имеет разрыв.
- 23. т.е. Для х2=2: Функция f(x) в точке х2=2 непрерывна.
- 24. 1 2 0 y x
- 25. так как ,
- 26. Вычислить предел функции:
- 27. Определение 2. Функция f(x) называется непрерывной, если
- 28. Сравнение бесконечно малых. Пусть
- 29. пример. Пусть
- 30. если ,
- 31. если ,
- 33. если ,
- 34. Для бесконечно
- 36. Найти предел, используя эквивалентные бесконечно малые функции:
Слайд 8
II. Второй замечательный предел
Теорема 1.
Переменная величина при n→∞
Слайд 9
Определение.
Предел переменной величины при
n→∞ называется числом е:
Из теоремы 1 и определения
Число е- иррациональное : е=2,7182818284…
Слайд 18
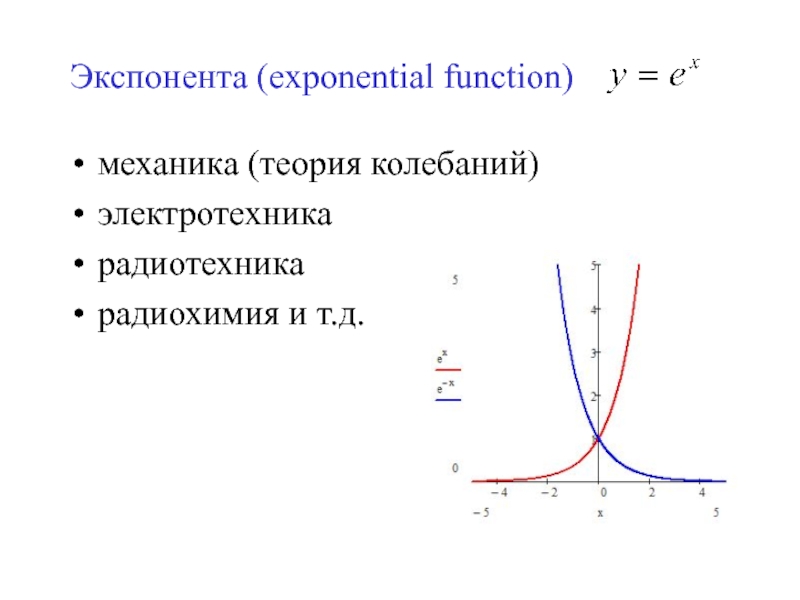
Экспонента (exponential function)
механика (теория колебаний)
электротехника
радиотехника
радиохимия и т.д.
Слайд 19Непрерывность функции.
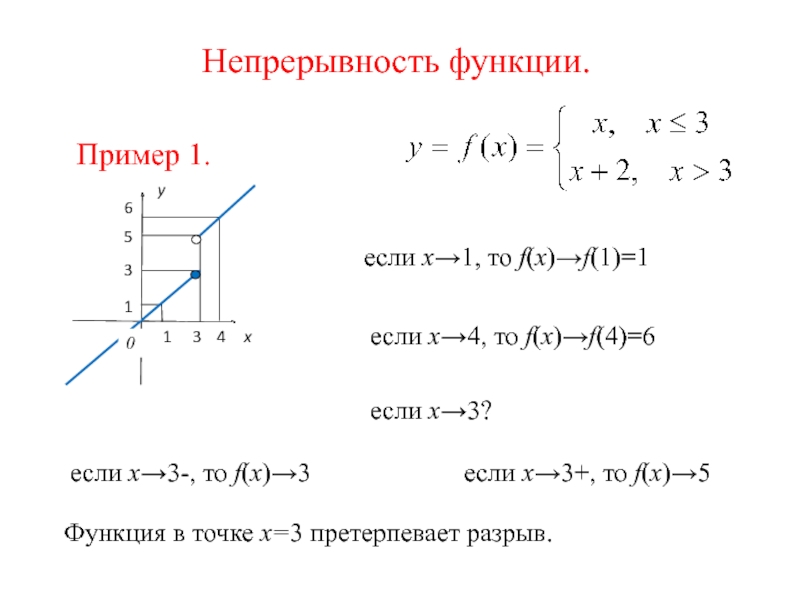
Пример 1.
если х→1, то f(x)→f(1)=1
если х→4, то f(x)→f(4)=6
если
если х→3-, то f(x)→3
если х→3+, то f(x)→5
6
5
3
4
3
1
1
0
y
x
Функция в точке х=3 претерпевает разрыв.
Слайд 20
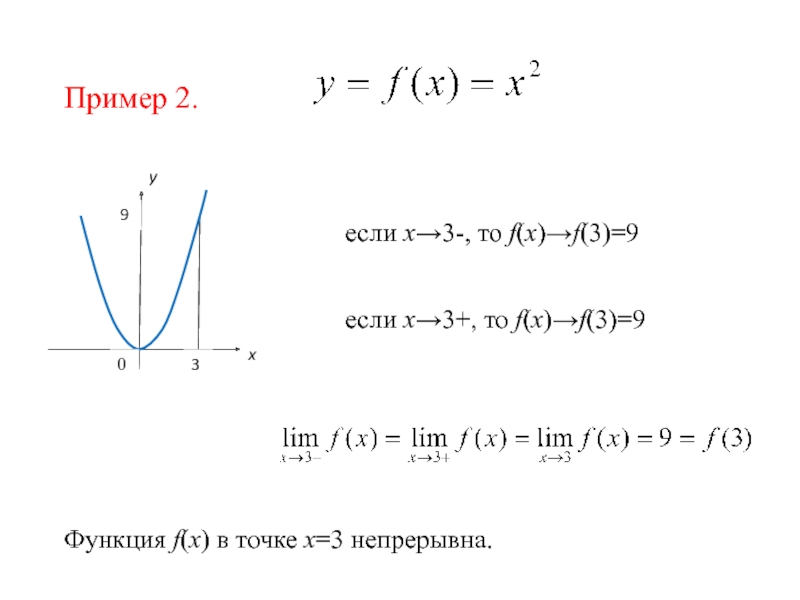
Пример 2.
если х→3-, то f(x)→f(3)=9
Функция f(x) в точке х=3 непрерывна.
если
9
3
0
y
x
Слайд 21Определение 1.
Функция f(x) называется непрерывной в точке х0, если
(функция непрерывна
Если равенство не выполняется, то говорят, что функция f(x) в точке х=х0 имеет разрыв.
Слайд 25
так как ,
то
Если функция непрерывна, то при отыскании её
Слайд 27Определение 2.
Функция f(x) называется непрерывной, если бесконечно малому приращению аргумента отвечает
0
y
x
x=x0+Δx
x0
Δx
y=f(x)
f(x0)
f(x)=f(x0+Δx)
Δy
приращение аргумента
приращение функции
Слайд 28Сравнение бесконечно малых.
Пусть при х→х0 функции α(х)→0 и β(х)→0.
Тогда:
1) если , то α(х) называется
бесконечно малой более высокого порядка, чем β(х).
(α(х) имеет более высокий порядок малости, чем β(х))
Слайд 30
если , то α(х) и β(х)
называются бесконечно малыми одного порядка
Пример.
Функции sin3x и sinx являются при х→0 бесконечно малыми одного порядка, т.к.
Слайд 31
если , то α(х) и β(х) называются
эквивалентными бесконечно малыми. (α(х)∽ β(х))
Пример.
Функции
Слайд 32
Пример.
Функции ln(1+x) и x являются при х→0 эквивалентными бесконечно малыми (ln(1+x)∽x)
Слайд 33
если , то α(х) называется
бесконечно малой n-го порядка относительно β(х)
Пример.
Функция
Слайд 34
Для бесконечно больших функций имеют место аналогичные правила сравнения.
Пример.
Функция
бесконечно большой более низкого порядка, чем , т.к.
Слайд 35
Примеры эквивалентных бесконечно малых функций:.
sin x ~ x
arctan x ~ x
arcsin
tan x ~ x
ln(1+x) ~ x
e x-1 ~ x
1-cos x ~ x2/2
a x-1 ~ x lna