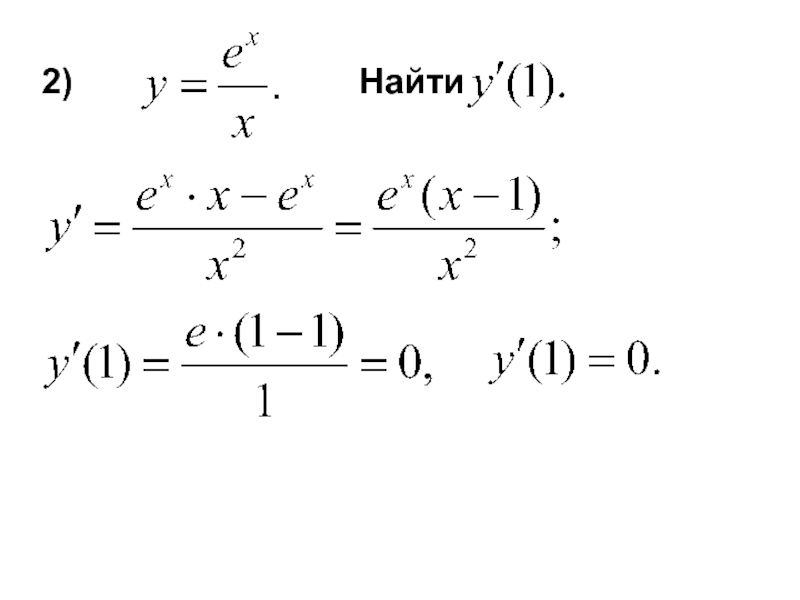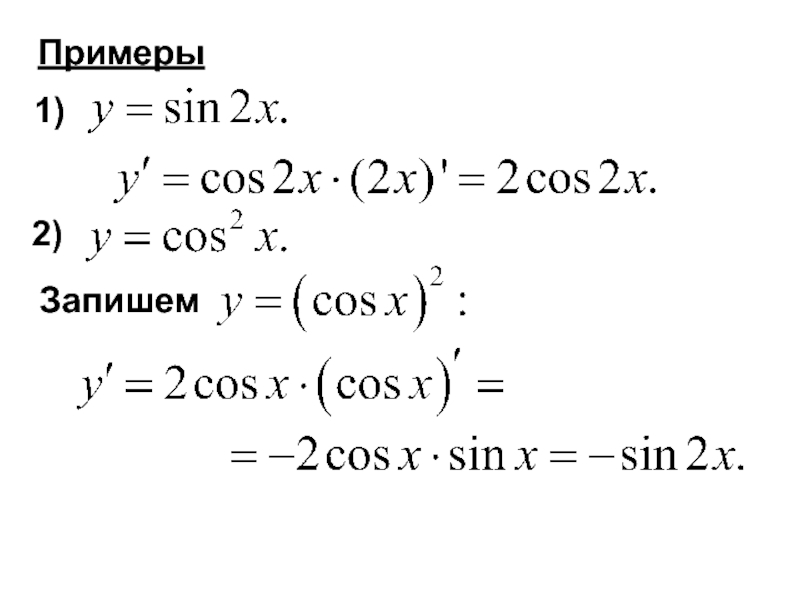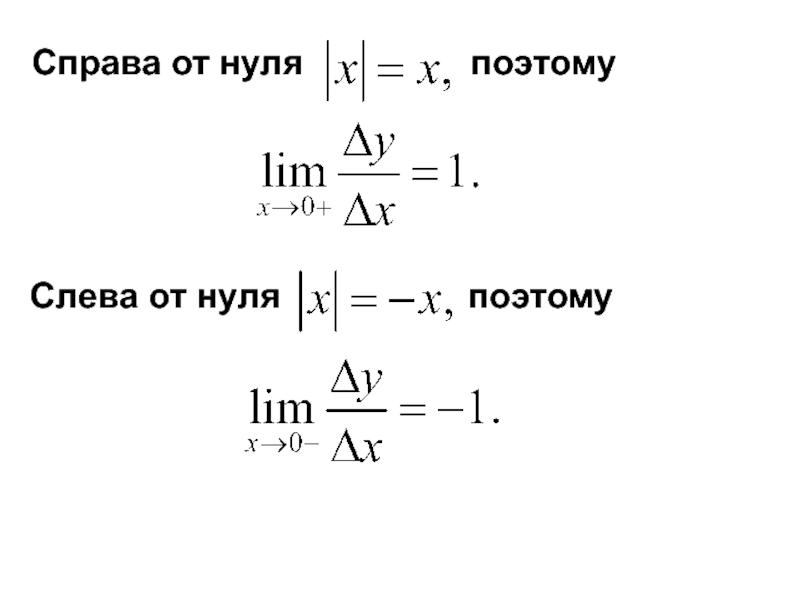Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции и их классификация.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции презентация
Содержание
- 1. Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции
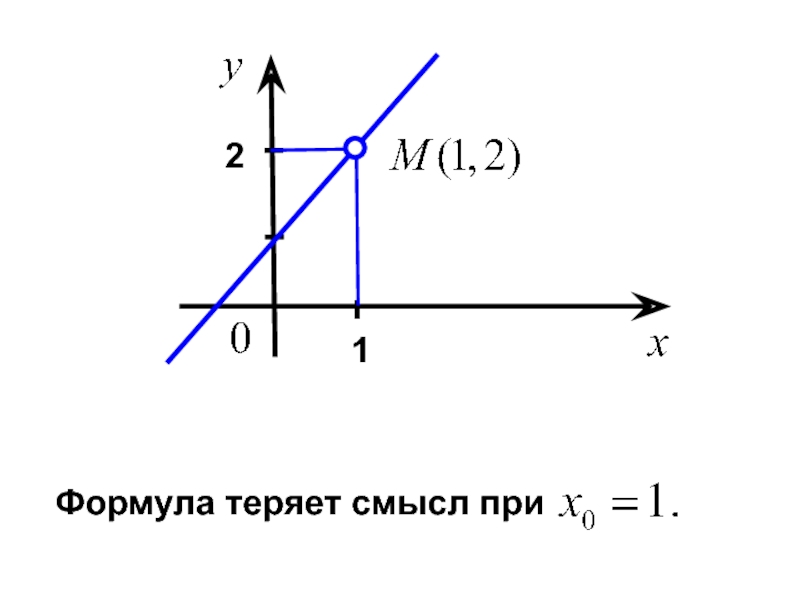
- 2. 1. Предел в точке. Рассмотрим пример. Построить график функции
- 3. 1 2
- 4. В этом случае пишут: По-другому: при
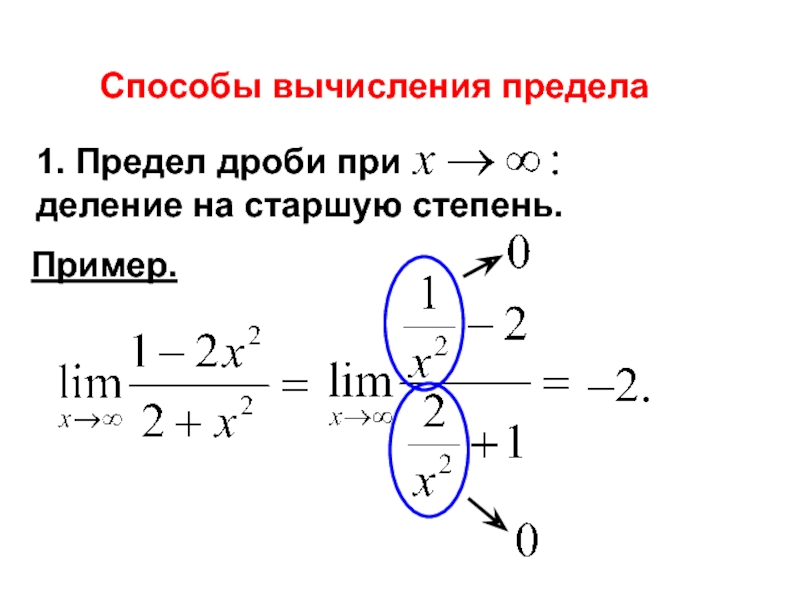
- 5. Способы вычисления предела 1. Предел дроби при
- 6. 2. Разложение на множители, когда Пример.
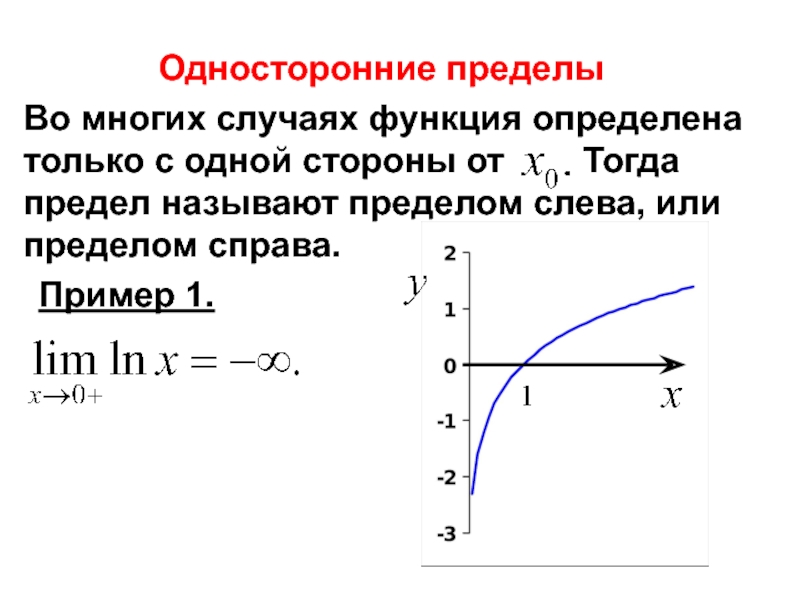
- 7. Односторонние пределы Пример 1.
- 8. Пример 2.
- 9. Опр. Функция
- 10. Опр. Если в точке
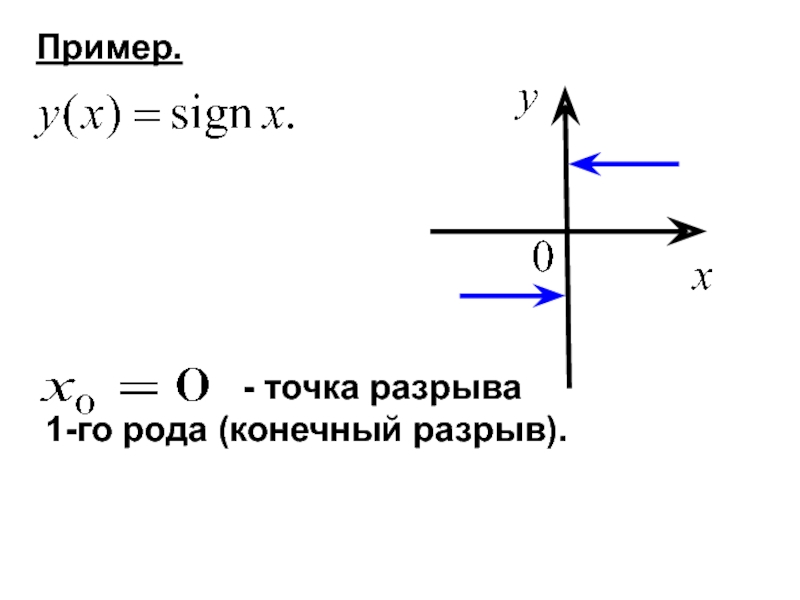
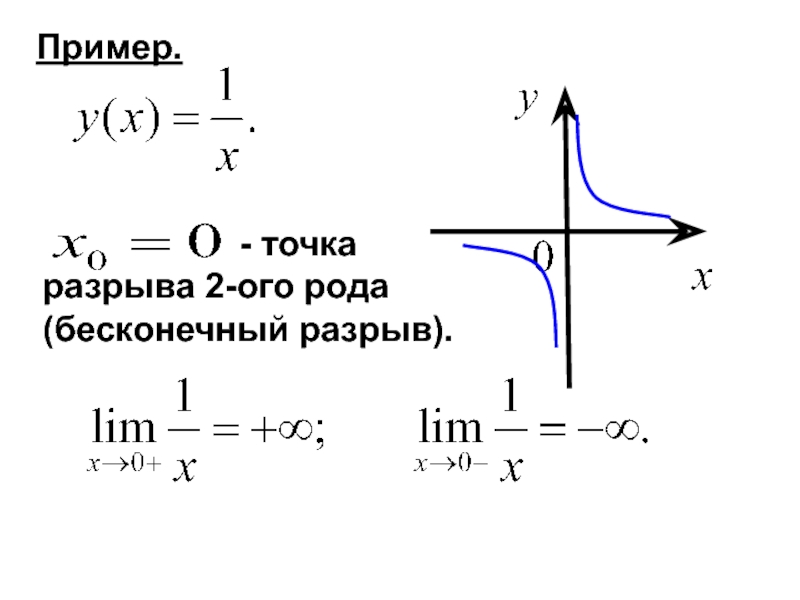
- 11. Пример.
- 12. Пример.
- 13. Тема: Производная функции, правила вычисления. Производная сложной функции. Производные высших порядков. Дифференциал функции.
- 14. Приращение аргумента и приращение функции Пусть
- 16. Пример. Найти производную функции Найдем Таким образом
- 17. Эта производная определена на всей числовой оси,
- 18. Геометрический смысл производной Угловой коэффициент касательной
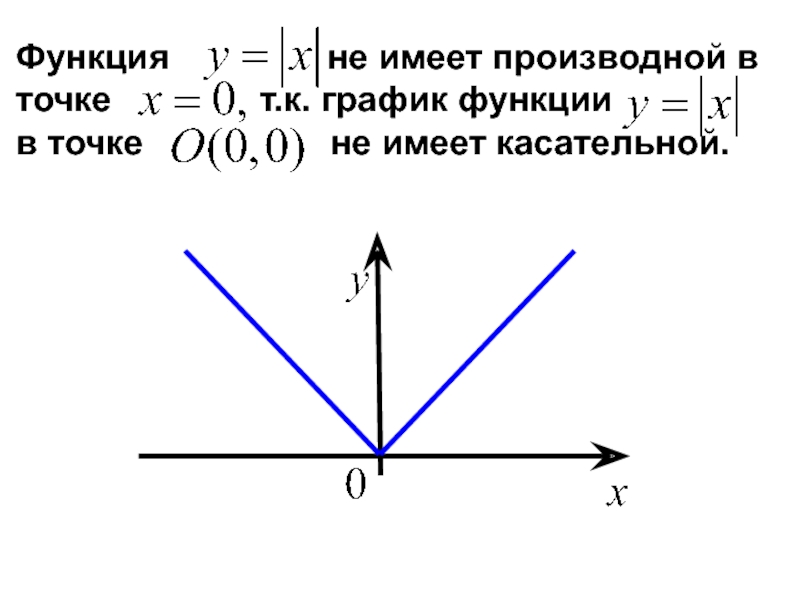
- 19. Функция
- 20. Таблица производных (степени)
- 21. Таблица производных (тригонометрия)
- 22. Таблица производных (arc-тригонометрия)
- 23. Основные правила дифференцирования Если функции
- 24. Если функции
- 25. 1)
- 26. 2)
- 27. Производная сложной функции Пусть
- 28. Примеры 1) 2) Запишем
- 29. Производные высших порядков Пусть функция
- 30. Аналогично,
- 31. 1) Найти производную третьего порядка от функции
- 32. Рассмотрим функцию Найдем Дифференциал функции
- 33. Приращение функции можно рассматривать как сумму двух слагаемых: - линейное относительно - нелинейное относительно
- 34. При
- 35. Теорема. Если функция
- 36. Примеры. Найти дифференциалы функций 1) 2)
- 37. Теорема. Если функция
- 38. Пример. В точке
- 39. Справа от нуля
- 40. Таким образом, отношение
1. Предел в точке. Рассмотрим пример.
Построить график функции
Слайд 9Опр. Функция
называется непрерывной в точке если
Все элементарные функции непрерывны на своей области определения.
Пример.
- непрерывные функции.
Слайд 10Опр. Если в точке функция не является непрерывной,
то - точка разрыва.
Рассматриваются точки разрыва 1-го и 2-ого рода.
Слайд 13Тема: Производная функции, правила вычисления. Производная сложной функции. Производные высших порядков.
Дифференциал функции.
Слайд 14Приращение аргумента
и приращение функции
Пусть дана функция
Рассмотрим два значения её аргумента: исходное и новое Разность называется приращением аргумента в точке и обозначается символом
Слайд 17Эта производная определена на всей числовой оси, так как при её
нахождении значение было выбрано произвольно.
Опр. Функция имеющая производную в точке называется дифференцируемой в этой точке. Функция называется дифференцируемой в интервале если она дифференцируема в каждой точке этого интервала.
Слайд 18
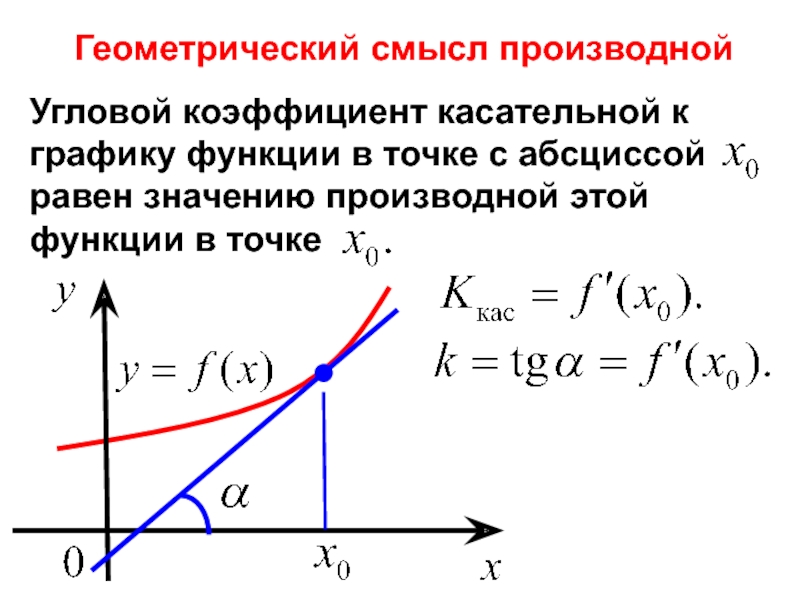
Геометрический смысл производной
Угловой коэффициент касательной к графику функции в точке с
абсциссой равен значению производной этой функции в точке
Слайд 23Основные правила дифференцирования
Если функции
и дифференцируемы в данной точке то в этой точке дифференцируемы и их сумма и произведение, причем
Слайд 24Если функции
и дифференцируемы в данной точке и то в той же точке дифференцируемо и их частное, причем
Слайд 29Производные высших порядков
Пусть функция
дифференцируема в некотором интервале.
Тогда её производная является функцией от Пусть эта функция также имеет производную. Эта производная называется второй производной и обозначается
Слайд 30Аналогично,
и т.д.:
Производные порядка выше первого называются производными высшего порядка.
Слайд 33Приращение функции можно рассматривать как сумму двух слагаемых:
- линейное относительно
-
нелинейное относительно
Слайд 34При оба слагаемых
стремятся к нулю, но второе слагаемое быстрее стремится к нулю. Поэтому при малых считают, что (т.е. считают, что приближенно равно линейной части). Эту часть называют главной частью приращения функции или дифференциалом.
Дифференциал функции обозначают
Слайд 35Теорема. Если функция
имеет в точке дифференциал, то она имеет в этой точке производную и наоборот, если функция имеет в точке производную, то она имеет в этой точке дифференциал.
Выражение для дифференциала записывается в форме
Слайд 37Теорема. Если функция дифференцируема в
точке то она в этой точке непрерывна.
Связь между дифференцируемостью и непрерывностью функции
Обратная теорема неверна: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми.
Слайд 40Таким образом, отношение при справа и
слева имеет различные пределы, а это значит, что при это отношение предела не имеет, т.е. производная в точке
не существует.
