Предел функции по Коши презентация

Предел функции по Коши

Пусть функция у = f(x) определена в окрестности точки x0. В самой точке x0 функция может быть и не определена.
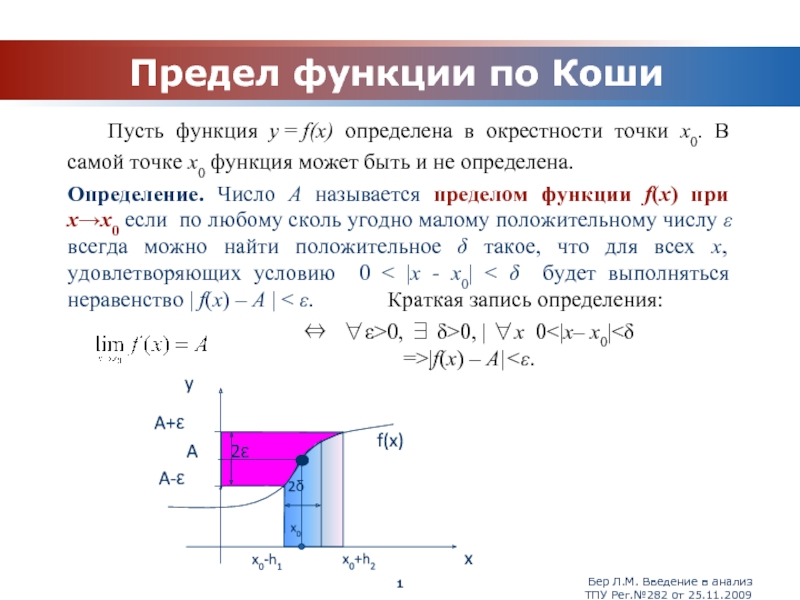
Определение. Число А называется пределом функции f(x) при x→x0 если по любому сколь угодно малому положительному числу ε всегда можно найти положительное δ такое, что для всех х, удовлетворяющих условию 0 < |x - x0| < δ будет выполняться неравенство | f(x) – A | < ε. Краткая запись определения:

⇔ ∀ε>0, ∃ δ>0, | ∀x 0<|x– x0|<δ =>|f(x) – А|<ε.

f(x) называется б. м.

f(x) называется б. б.

f(x) называется б. б.

∀ε>0, ∃ δ>0, |
∀x 0< | х – x0| <δ =>|f(x) – A|<ε

∀ε>0, ∃ δ>0, |
∀x 0< | х – x0| <δ =>|f(x)|<ε

0

∀ε>0, ∃ δ>0, |
∀x | х| >1/δ =C =>|f(x) – A|<ε

Предел функции по Гейне

Пусть функция у = f(x) определена в окрестности точки x0. В самой точке x0 функция может быть и не определена.

Определение. Вещественное число А называется пределом функции f(x) при х→x0, если для любой последовательности {xn} значений аргумента, стремящейся к x0 соответствующая последовательность значений функции {f(xn)} сходиться к А.

При этом предполагается, что {xn} такая, что xn ∈ D(f) и


Теорема 1. Определение предела функции по Гейне и по Коши эквивалентны.

.

Свойства пределов

Если предел функции f(x) при х→x0 существует, то он единственный.
Если функция f(x) при х→ x0 имеет конечный предел, то она ограничена в некоторой окрестности точки x0.
Функция имеет предел тогда и только тогда, когда ее можно представить как сумму постоянной, равной этому пределу и бесконечно малой величины.

Свойства пределов

Если функции f(x) и g(x) имеют предел при х→x0 , то их сумма, разность, произведение и частное имеют предел при х→ x0, причем
;
;


Если функция f(x) имеет предел при х→x0, то произведение с*f(x) имеет предел при х→x0, с – константа, причем .
Пусть и существует проколотая окрестность U*(x0,γ) такая, что f(x) > 0 ∀x ∈ U*(x0,γ), тогда А ≥ 0.

Свойства пределов

Пусть и пусть и f(x) < g(x) ∀x∈U*(x0, γ) (или f(x) ≤ g(x)), тогда А ≤ B.
Пусть ∀x ∈ U*(x0,γ) выполняется f(x) ≤ g(x) ≤ ϕ(x). Если существует и существует , причем , то существует и .
Свойство о пределе композиции функций.
Пусть и существуют
тогда g(f(x))=g ° f имеет предел при х→x0, причем
.

Свойства б.м. функции

Сумма, разность, произведение двух б.м. при x → x0 есть функция б.м. при x → x0.
Пусть α(x) - б.м. при x → x0, f(x) – ограниченна в U*( x0, δ), тогда α(x) f(x) – б.м. при x → x0.
Если α(x) - б.м. при x → x0, то с ⋅α(x) - б.м. при x →  x0, с-константа.
Если функция у = f(x) – б.м. при x→ x0 и f(x) ≠ 0 в некоторой окрестности точки x0, то функция y=1/f(x) – б.б. при x → x0. Если функция у = f(x) - б.б. при x → x0, и f(x)≠ 0 в некоторой окрестности точки x0, то функция y = 1/f(x) – б.м. при x → x0.
О роли б.м. в теории пределов.

Односторонние пределы

Определение. Число А называется пределом функции f(x) при х→x0 слева, если для любого ε>0 существует такое δ>0, что для всех х, отвечающих условию 0 < х0 – x < δ выполняется неравенство |f(x) – А|<ε.
Число А называется пределом функции f(x) при х→x0 справа, если для любого ε>0 существует такое δ>0, что для всех х, отвечающих условию 0 < х – x0< δ выполняется неравенство |f(x) – А|<ε.
Обозначение:
или f(x0 – 0) предел слева при х→x0,
или f(x0+0) предел справа при х→x0.

Односторонние пределы

Теорема 2. (О существовании конечного предела.)
Пусть x0∈R. Функция f(x) имеет конечный предел при х→ x0 тогда и только тогда, когда существуют конечные и равные между собой пределы = =A, при этом .

Замечание 1. Все свойства пределов остаются верными и в случае односторонних пределов.

Замечание 2. Определение одностороннего предела на языке последовательностей дается также как и определение предела при х→ x0 с той лишь разницей, что для последовательности {xn} должно выполняться условие xn < x0 для предела слева и xn > x0 для предела справа.

Замечательные пределы

Теорема 3. Предел отношения sin x к своему аргументу x равен единице, когда аргумент стремится к нулю, т. е.
– 1 замечательный предел.


(или ) – 2 замечательный предел.

Следствия:

1) , 2) , 3) .

Сравнение бесконечно малых

Пусть α(x), β(x) – б.м. при x → x0, где x0 – конечно или б.б.
Определение. Если , то говорят, что α(x) б.м. более высокого порядка, чем β(x) при х → x0, или что β(x) - б.м. низшего порядка относительно α(x). Обозначение: α(x) =о(β(x)).

Определение. Если , где с = const ≠ 0, то α(x) и β(x) называют б.м. одного порядка.
В частности, если , то α(x) и β(x) называются эквивалентными. Обозначение: α(x) ~ β(x).

Определение. Б.м. α(x) называется бесконечно малой порядка k относительно б.м. β(x), если , где с = const ≠ 0.

Теорема 2. (О замене б.м. на эквивалентную.)
Если α(x) ~ α1(x), β(x) ~ β1(x) и , то , т.е. предел отношения б.м. не меняется при замене их эквивалентными бесконечно малыми:

Таблица эквивалентностей

Пусть α(х) → 0 при x → x0. Тогда при x → x0

~

Теорема 2. (Критерий эквивалентности б.м.)
Б.м. α(x) и β(x) при x → x0 эквивалентные б.м. тогда и только тогда, когда их разность α(x) – β(x) – б.м. более высокого порядка, чем α(x) и β(x) при x → x0.
Замечание 1. Аналогично б.м. можно сравнивать и б.б., а именно если f(x) и ϕ(x)-б.б. при x → x0 и
− f(x) б.б. более высокого порядка, чем ϕ(x);
− f(x) б.б. более низкого порядка, чем ϕ(x);
− f(x) и ϕ(x) эквивалентные б.б. при x → x0.
Замечание 2. Теоремы 1 и 2 для б.б. функций остаются верными с той лишь разницей, что главной частью б.б. функции является б.б. более высокого порядка.

Спасибо за внимание