- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение треугольника по трем элементам. (Урок 56) презентация
Содержание
- 1. Построение треугольника по трем элементам. (Урок 56)
- 2. ПОВТОРЕНИЕ Что называется расстоянием от точки
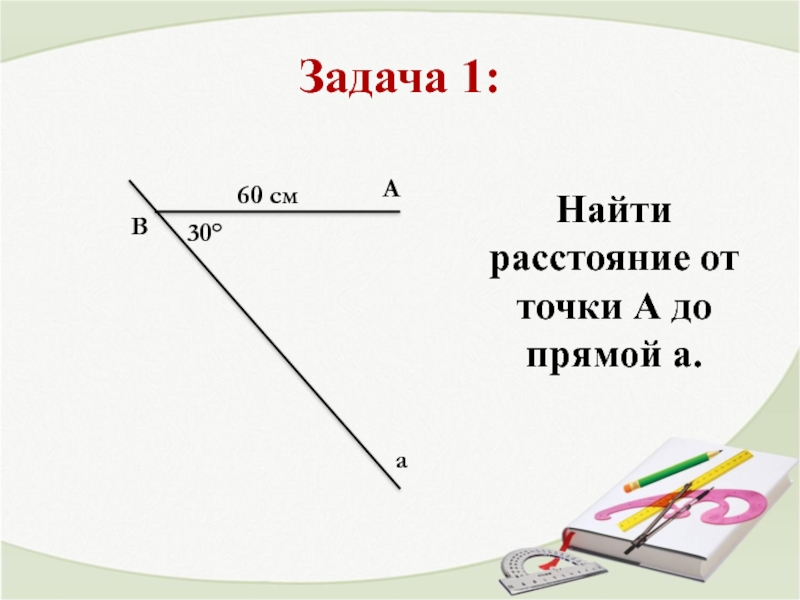
- 3. Задача 1: 30° В А а
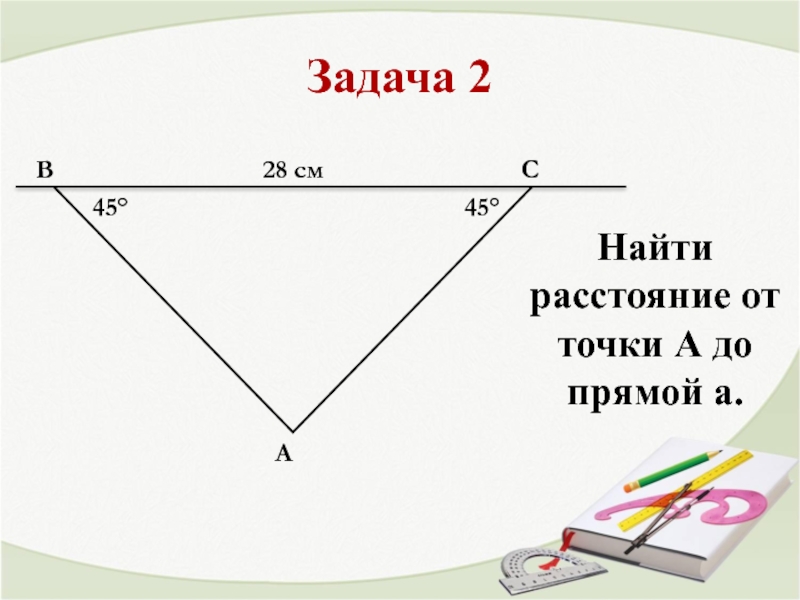
- 4. Задача 2 45° 45° 28 см
- 5. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ. Как вы
- 6. ВСПОМНИМ Как построить отрезок, равный данному. Как построить угол, равный данному. Как построить биссектрису угла.
- 7. Задача 1: Построение треугольника по двум сторонам и углу между ними.
- 8. D С
- 9. При любых данных отрезках AB=P1Q1, AC=P2Q2 и
- 10. Задача 2: Построение треугольника по стороне и прилежащим к ней углам.
- 11. D С
- 12. Задача 3: Построение треугольника по трем сторонам.
- 13. С Построим луч а.
- 14. Задача не всегда имеет решение. Во всяком
- 15. Домашнее задание: §4 пункт 39 вопросы
- 16. Спасибо за внимание!
ПОВТОРЕНИЕ Что называется расстоянием от точки до прямой? Сформулируйте свойство параллельных прямых. Что называется расстояние между двумя прямыми? Сформулируйте теорему, обратную свойству параллельных прямых.
Слайд 1Выполнила
учитель математики
МБОУ Школа №99 г.о.Самара
Сычева Елена Александровна
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК.
Слайд 2ПОВТОРЕНИЕ
Что называется расстоянием от точки до прямой?
Сформулируйте свойство параллельных прямых.
Что называется
расстояние между двумя прямыми?
Сформулируйте теорему, обратную свойству параллельных прямых.
Сформулируйте теорему, обратную свойству параллельных прямых.
Слайд 5ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ.
Как вы думаете, чем мы с вами
сегодня будем заниматься на уроке? Какая тема нашего урока?
Слайд 6ВСПОМНИМ
Как построить отрезок, равный данному.
Как построить угол, равный данному.
Как построить биссектрису
угла.
Слайд 8
D
С
∠hk
h
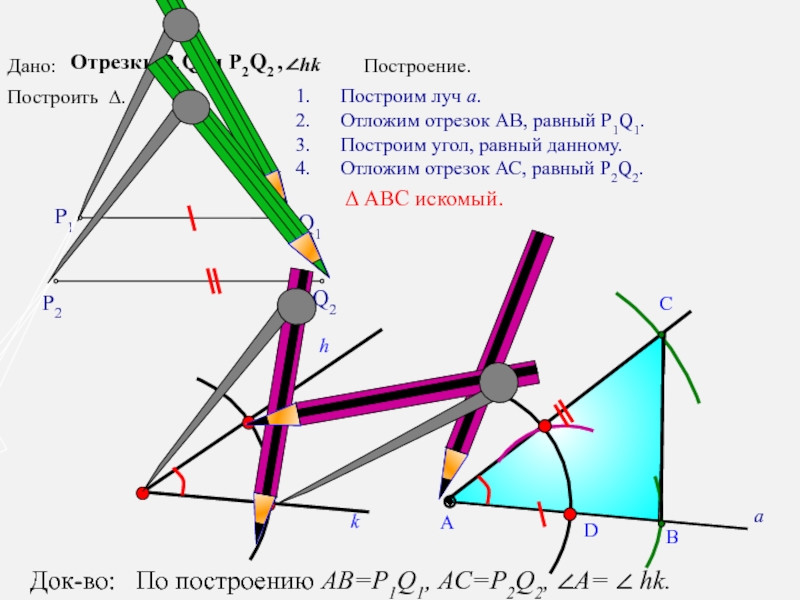
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол,
равный данному.
Отложим отрезок АС, равный P2Q2.
Отложим отрезок АС, равный P2Q2.
В
А
Δ АВС искомый.
Дано:
Отрезки Р1Q1 и Р2Q2 ,
Q1
P1
P2
Q2
а
k
Док-во: По построению AB=P1Q1, AC=P2Q2, ∠A= ∠ hk.
Построить ∆.
Построение.
Слайд 9При любых данных отрезках AB=P1Q1, AC=P2Q2 и данном неразвернутом ∠hk искомый
треугольник построить можно.
Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.
Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.
Слайд 11
D
С
∠h1k1 , ∠h2k2
h2
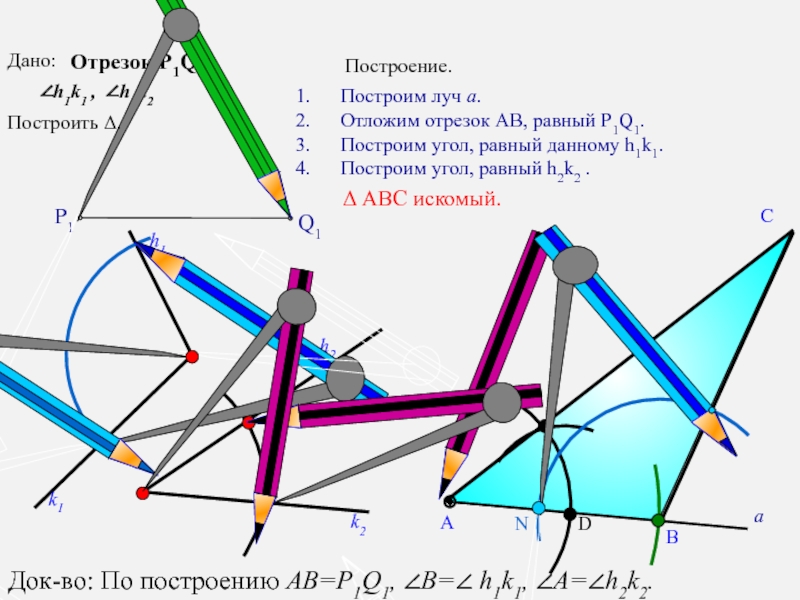
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим
угол, равный данному h1k1.
Построим угол, равный h2k2 .
Построим угол, равный h2k2 .
В
А
Δ АВС искомый.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
h1
k1
N
Док-во: По построению AB=P1Q1, ∠В=∠ h1k1, ∠А=∠h2k2.
Построить Δ.
Построение.
Слайд 13
С
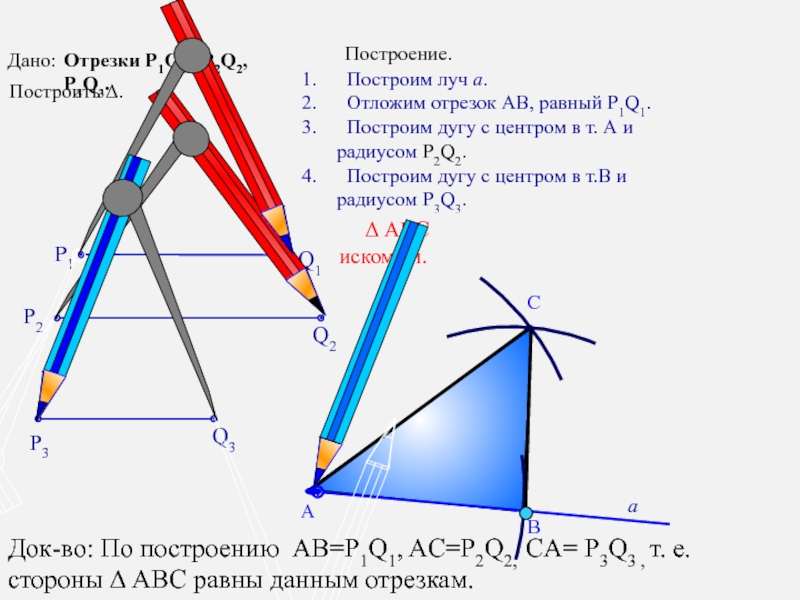
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром в
т. А и
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
В
А
Δ АВС искомый.
Дано:
Отрезки Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
Док-во: По построению AB=P1Q1, AC=P2Q2, CA= P3Q3 , т. е. стороны Δ ABC равны данным отрезкам.
Построить Δ.
Построение.
Слайд 14Задача не всегда имеет решение.
Во всяком треугольнике сумма любых двух сторон
больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.
Слайд 15Домашнее задание:
§4 пункт 39
вопросы 21,22
№284 (разобрать устно)
№274
повторить 5 задач на
построение.
