- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильні многогранники презентация
Содержание
- 1. Правильні многогранники
- 2. Многогранник – це геометричне тіло, обмежене
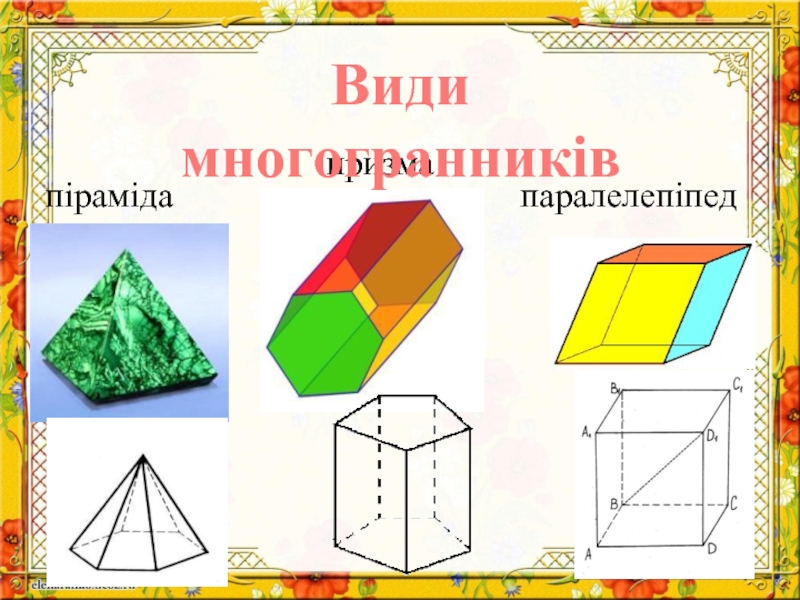
- 3. піраміда призма паралелепіпед Види многогранників
- 4. Піраміда называется правильною, якщо в основі
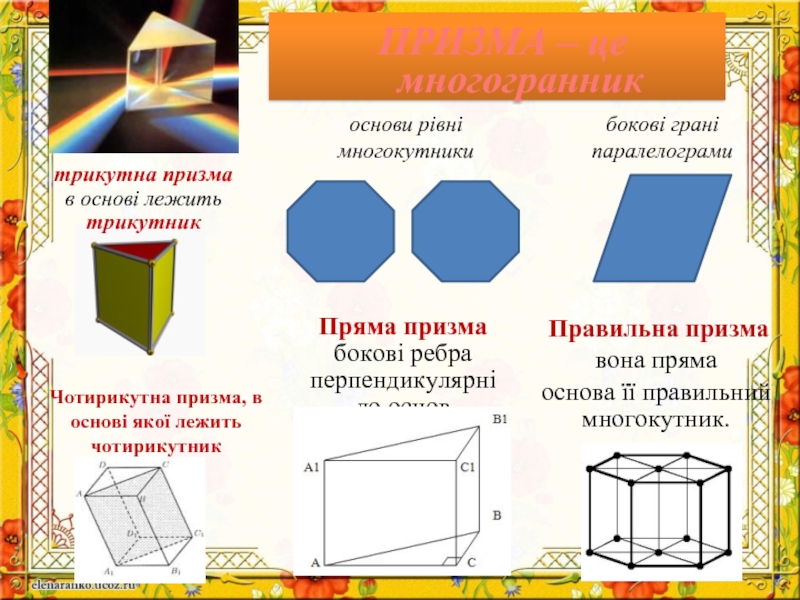
- 5. Правильна призма вона
- 6. Паралелепіпед – це призма
- 7. Математичний диктант. Знайдіть: а) апофему зрізаної піраміди;
- 8. Епіграф. Правильних многогранників надзвичайно мало, але цей
- 9. Правильні многогранники Тетраедр Гексаедр(Куб) Октаедр Ікосаедр Додекаедр
- 10. Визначення правильних многогранників, які даються в різних
- 11. Тетраедр ( від ,,тетра”- чотири і грецького
- 12. Тетраедр У різних хімічних реакціях застосовується сурьменістичний
- 13. Гексаедр (куб) гексаедр (куб) - земля Гексаедр
- 14. Куб Правильні багатогранники - широко поширені в
- 15. Октаедр октаедр-повітря (від грецького okto -
- 16. Октаедр При виробництві алюмінію користуються алюмінієво-калієвими кварци
- 17. Додекаедр додекаедр-всесвіт! Додекаедр втілював у собі "все
- 18. Додекаедр. Отримання сірчаної кислоти , заліза ,
- 19. Ікосаедр ікосаедр-вода ікосаедр символизував воду, так
- 20. Ікосаедр Скелет одноклітинного організму феодаріі. Ікоса́едр — правильний опуклий
- 21. Віруси, побудовані тільки з нуклеїнової кислоти і
- 22. Формули для обчислення площ поверхонь і об’ємів правильних многогранників
- 23. Многогранник — геометрична фігура, частина простору, обмежена замкненою поверхнею, що
- 25. Теорема Ейлера: Число вершин - число
- 26. Мозковий штурм Задача: Визначити кількість граней, вершин
- 27. Математика - гімнастика для розуму, СТЕРЕОМЕТРіЯ - витамін для мозку.
- 28. Висновок Отже, як ви помітили многогранники оточують
- 29. Підсумок Правильні многранники існували на Землі задовго
Слайд 2
Многогранник – це геометричне тіло, обмежене плоскими многокутниками.
Плоскі многоугокутники
називаются гранями многогранника
стороны многокутника –
ребрами многогранника
вершины многокутника –
вершинами многогранника.
Слайд 4Піраміда называется правильною,
якщо в основі лежить правильный многокутник, а вершина
в центр основи
Піраміда - це многогранник
Слайд 6Паралелепіпед – це призма
Слайд 7Математичний диктант.
Знайдіть:
а) апофему зрізаної піраміди;
б) площу бічної грані;
в) площу
г) площу меншої основи;
д) площу більшої основи;
е) площу поверхні зрізаної піраміди.
Дано правильну зрізану піраміду, бічне ребро якої
дорівнює 5 см, а в основах лежать:
варіант І — трикутники (рис. 1);
варіант II — квадрати (рис. 2)
зі сторонами 1 см і 9 см.
Слайд 8Епіграф. Правильних многогранників надзвичайно мало, але цей дуже скромний за кількістю
Л.Керролл
Слайд 10Визначення правильних многогранників, які даються в різних підручниках, рекомендованих для загальноосвітніх
«Опуклий багатогранник називається правильним, якщо всієї його грані – правильні багатокутники й у кожній його вершині сходиться однакова кількість ребер». (Л.С. Атанасян «Геометрія, 10-11 класи» )
“Багатогранник називається правильним, якщо всі його грані - рівні правильні багатокутники, а всі його вершини однаково віддалені від деякої точки - центра правильного багатокутника” (Г. П. Бевз, В. Г. Бевз, Н. Г. Владимирова. Геометрія 7-11 класи )
“Якщо всі грані опуклого багатогранника - конгруентні правильні багатокутники й число ребер, що виходять із кожної вершини, однаково, то багатогранник називається правильним” (В. М. Клопський, З. А. Скопець, М. И. Ягодовський. Геометрія. Навчальний посібник для 9-10 класів середньої школи).
Слайд 11Тетраедр
( від ,,тетра”- чотири і грецького ,,hedra” - грань) складається з
тетраедр-вогонь
Тетраедр символізував вогонь,
т.к. його вершина напрямлена вгору.
Слайд 12Тетраедр
У різних хімічних реакціях застосовується сурьменістичний сірчанокислий натрій - речовина, синтезоване
Слайд 13Гексаедр (куб)
гексаедр (куб) - земля
Гексаедр (куб) символізував землю,
так як «найстійкіший»
(від грецького ,,гекса” - шість и ,,hedra” - грань) має 6 квадратних граней, в кажній його вершині сходятся 3 ребра.
Гексаедр більш відомий як куб (від латинського ,,cubus”; від грецького ,,kubos”.
Слайд 14Куб
Правильні багатогранники - широко поширені в природі. Підтвердженням тому служить форма
Слайд 15Октаедр
октаедр-повітря
(від грецького okto - вісім и hedra - грань) має
в кажній вершині сходяться 4 ребра.
Октаэдр символізував повітря,
як "найповітряніший"
Слайд 16Октаедр
При виробництві алюмінію користуються алюмінієво-калієвими кварци , монокристал яких має форму
Кристал кварцу
Діамант
Слайд 17Додекаедр
додекаедр-всесвіт!
Додекаедр втілював у собі "все суще", символізував все світотворення, вважався головним.
(від
сходятся 3 ребра.
Слайд 18Додекаедр.
Отримання сірчаної кислоти , заліза , особливих сортів цементу не обходиться
Кристал
прикраса
Клітина ВІЧ
Слайд 19Ікосаедр
ікосаедр-вода
ікосаедр символизував воду,
так як він «обтічний»
(від грецького eikosi -
в кожній вершині сходиться 5 ребер
Слайд 20Ікосаедр
Скелет одноклітинного організму феодаріі.
Ікоса́едр — правильний опуклий багатогранник, двадцятигранник, одне з Платонових тіл.
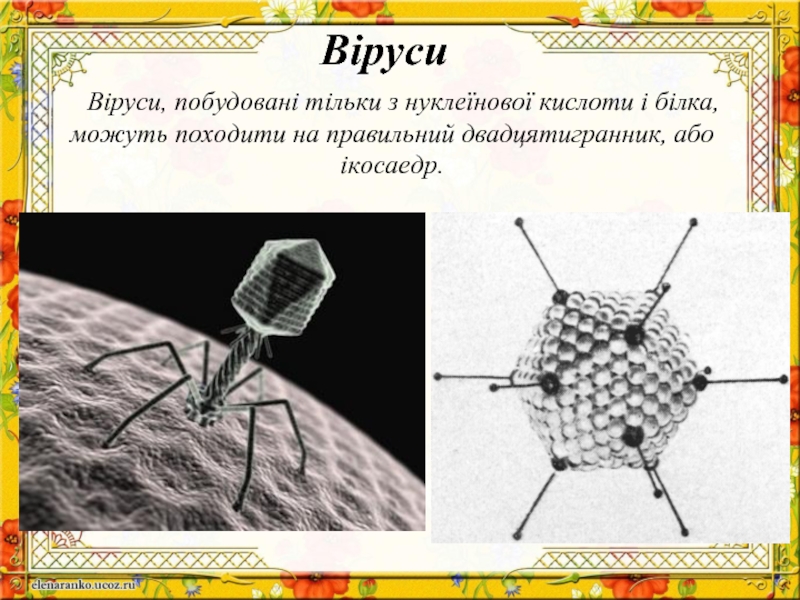
Слайд 21Віруси, побудовані тільки з нуклеїнової кислоти і білка, можуть походити на
Віруси
Слайд 23Многогранник — геометрична фігура, частина простору, обмежена замкненою поверхнею, що складається з плоских багатокутників, які
Многогранник з n гранями називають n-гранник. Зокрема,
тетраедр — 4-гранник,
додекаедр — 12-гранник,
ікосаедр — 20-гранник.
октаедр — 8-гранник
куб — 6-гранник
Визначення:
Слайд 25Теорема Ейлера:
Число вершин - число ребер + число граней =2
Швейцарський,
автор більш ніж 800 робіт по математичному аналізу, диференційній геометрії, теорії музики та ін..
Леонард Эйлер
(1707-1783)
Число вершин, ребер та граней правильних многокутників повязане одне з одним цікавим співвідношенням.
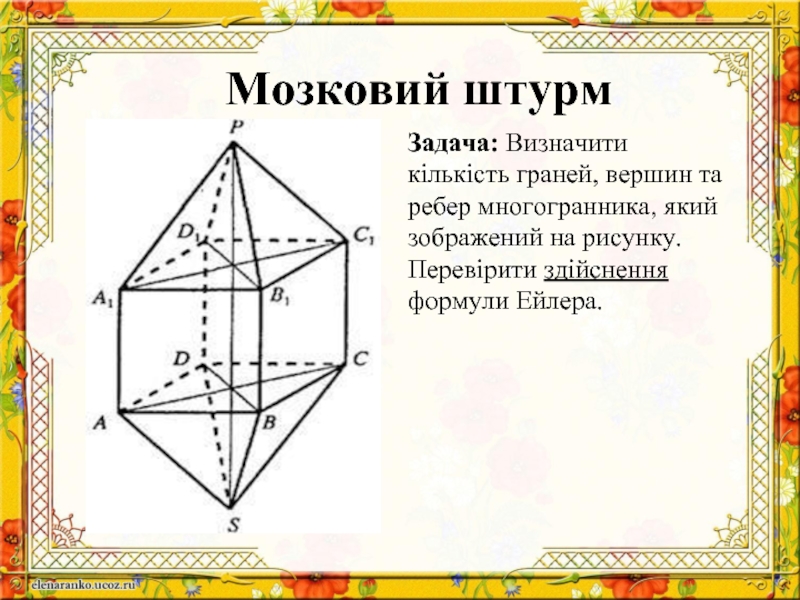
Слайд 26Мозковий штурм
Задача: Визначити кількість граней, вершин та ребер многогранника, який зображений
Слайд 28Висновок
Отже, як ви помітили многогранники оточують нас повсюди: в побуті, природі,
Слайд 29Підсумок
Правильні многранники існували на Землі задовго до появи на ній людини
Але тільки геометр побачив в них порядок і систему задовго до того, як фізики проникли в таємницю будови речовини.
Геометрія з її прозорою логікою, чіткістю побудов відкрила зовсім нове бачення правильних многогранників та їх нове застосування.