- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Позиционные системы счисления, отличные от десятичной презентация
Содержание
- 1. Позиционные системы счисления, отличные от десятичной
- 2. Основанием позиционной системы счисления может быть любое
- 3. Определение Записью натурального числа x в
- 4. Теорема Пусть p≥2 – заданное натуральное число.
- 5. Доказательство: 1. Разделим число x на
- 6. 2. Единственность представления числа х
- 7. Например: В троичной системе (p=3)
- 8. На числовой прямой троичная система счисления может
- 9. Сравнение чисел и арифметические действия
- 10. Задание №1 Сравнить числа x и y,
- 11. Задание №2 Найти сумму чисел в троичной
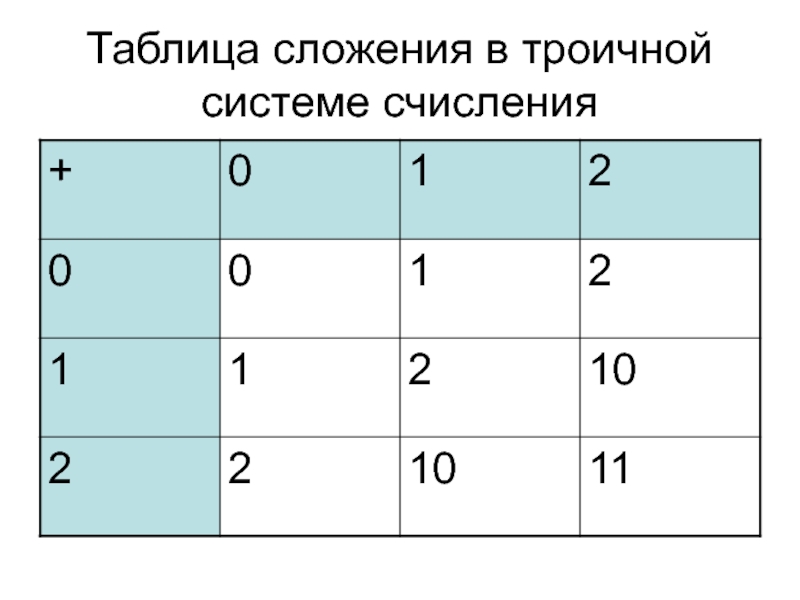
- 12. Таблица сложения в троичной системе счисления
- 13. ___________ Применив, таблицу сложения, имеем:
- 14. Задание № 3 Запишите следующие числа в
- 15. Ответ: 1) а= 2) b= 3)c=
- 16. Задание №4. Запишите в десятичной системе числа:
- 17. Ответы: Число Число
- 18. Вывод: Чтобы число, записанное в p-ичной
- 19. Задание №5. Запишите число в p-ичной системе
- 20. Ответ : Разделим число 35 на 2
- 21. Следовательно: 35= Выпишем последнее частное и остатки, начиная с последнего.
- 22. Ответ: Разделим 124 разделим на 5 Имеем:
- 23. Следовательно: 124=
- 24. Вывод: чтобы число, записанное в
- 25. Первое неполное частное снова делят на p-
- 26. Первой значащей цифрой числа х является последнее
- 27. Спасибо за внимание
Основанием позиционной системы счисления может быть любое число p≥2. P=2 – двоичная система P=3 – троичная система P=8 – восьмеричная система
Слайд 2Основанием позиционной системы счисления может быть любое число p≥2.
P=2 – двоичная
система
P=3 – троичная система
P=8 – восьмеричная система
P=3 – троичная система
P=8 – восьмеричная система
Слайд 3Определение
Записью натурального числа x в системе счисления с основанием p
называется его представление в виде:
где коэффициенты
принимают значения 0,1,2,…,p-1 и
≠ 0
Слайд 4Теорема
Пусть p≥2 – заданное натуральное число.
Тогда любое натуральное число
x представимо, и притом единственным образом в виде:
Краткая запись числа x =
____________
Слайд 5Доказательство:
1. Разделим число x на
Имеем:
Далее
Процесс деления остатка на
- основание системы – конечен.
Следовательно, число x представимо в виде суммы разрядных слагаемых.
Слайд 6
2. Единственность представления числа х в виде суммы разрядных слагаемых следует
из единственности деления с остатком.
Слайд 7Например:
В троичной системе (p=3)
можно записать в виде:
Читать следует так: «два,
ноль, один, два в троичной системе счисления»
Слайд 8На числовой прямой троичная система счисления может быть представлена:
х
0 1
2 10 1112 20 21 22
100
Слайд 9
Сравнение чисел и арифметические действия в любой «p-ичной» системе счисления выполняются
так же как и в десятичной.
Надо лишь иметь для системы с основанием p соответствующие таблицы сложения и умножения однозначных чисел
Надо лишь иметь для системы с основанием p соответствующие таблицы сложения и умножения однозначных чисел
Слайд 10Задание №1
Сравнить числа x и y, если
Следовательно, x>y
т.к. выполняется
3 условие теоремы о сравнении чисел в десятичной системе счисления.
Слайд 11Задание №2
Найти сумму чисел в троичной системе.
Запишем числа согласно алгоритму сложения
_________
Используя
таблицу сложения в троичной системе, имеем:
Слайд 18Вывод:
Чтобы число, записанное в p-ичной системе, представить в десятичной, нужно:
Записать число
в виде суммы разрядных слагаемых в p-ичной системе счисления.
Выполнить записанные действия в десятичной системе счисления.
Выполнить записанные действия в десятичной системе счисления.
Слайд 19Задание №5. Запишите число в p-ичной системе счисления:
Число 35 в двоичной
системе счисления;
Число 124 в пятеричной системе счисления
Число 124 в пятеричной системе счисления
Слайд 20Ответ :
Разделим число 35 на 2 – основание системы.
Имеем: 35=2·17+1
Затем-частное 17разделим
на 2-основание системы
Имеем: 17=2·8+1
Затем частное 8 разделим на 2
Имеем: 8=2·4+0
Затем частное 4 разделим на2
Имеем: 4=2·2+0
Затем частное 2 разделим на 2
Имеем: 2=2·1+0.
Последнее частное 1 меньше делителя 2.
Процесс деления закончен
Имеем: 17=2·8+1
Затем частное 8 разделим на 2
Имеем: 8=2·4+0
Затем частное 4 разделим на2
Имеем: 4=2·2+0
Затем частное 2 разделим на 2
Имеем: 2=2·1+0.
Последнее частное 1 меньше делителя 2.
Процесс деления закончен
Слайд 22Ответ:
Разделим 124 разделим на 5
Имеем: 124=5·24+4
Разделим частное 24 на 5
Имеем 24=5·4+4
Последнее
частное 4 <5.
Деление закончено
Деление закончено
Слайд 24 Вывод: чтобы число, записанное в десятичной системе счисления, представить в p-ичной
нужно:
Число х разделить (в десятичной системе счисления) на p- основание системы счисления с остатком.
Первый остаток – есть последняя значащая цифра числа х в p-ичной системе счисления.
Слайд 25Первое неполное частное снова делят на p- основание системы счисления с
остатком.
Второй остаток – есть следующая слева значащая цифра числа х в p-ичной системе счисления.
Процесс деления продолжаем, пока
Неполное частное не станет меньше p.
Второй остаток – есть следующая слева значащая цифра числа х в p-ичной системе счисления.
Процесс деления продолжаем, пока
Неполное частное не станет меньше p.
Слайд 26Первой значащей цифрой числа х является последнее частное.
Второй значащей цифрой числа
х является последний остаток.
Замечание: остатки могут принимать значения 0, 1,2,…,p-1.
Замечание: остатки могут принимать значения 0, 1,2,…,p-1.
