- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Позиционные и метрические задачи. Задание прямой на эпюре Монжа. (Лекция 3) презентация
Содержание
- 1. Позиционные и метрические задачи. Задание прямой на эпюре Монжа. (Лекция 3)
- 2. 1. Позиционные задачи Задачи, в которых
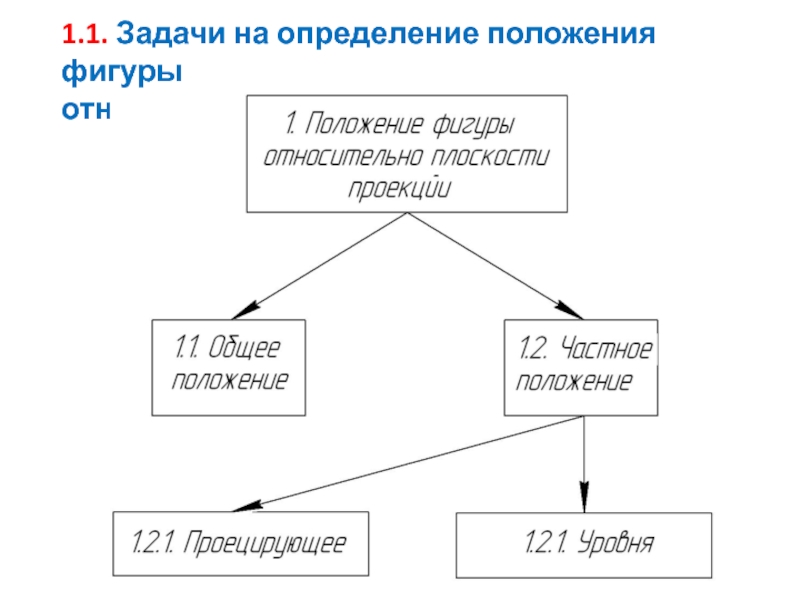
- 3. 1.1. Задачи на определение положения фигуры относительно плоскостей проекций
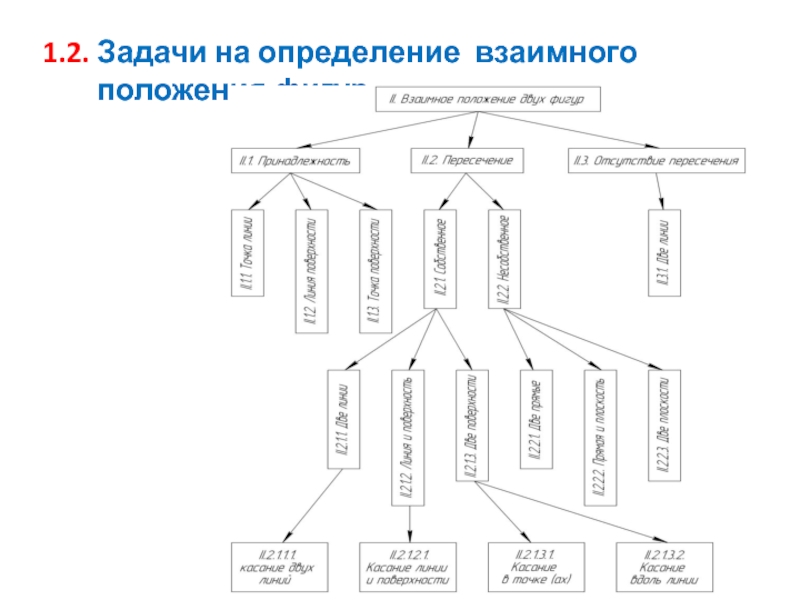
- 4. 1.2. Задачи на определение взаимного положения фигур
- 5. 2. Метрические задачи Задачи, в которых требуется
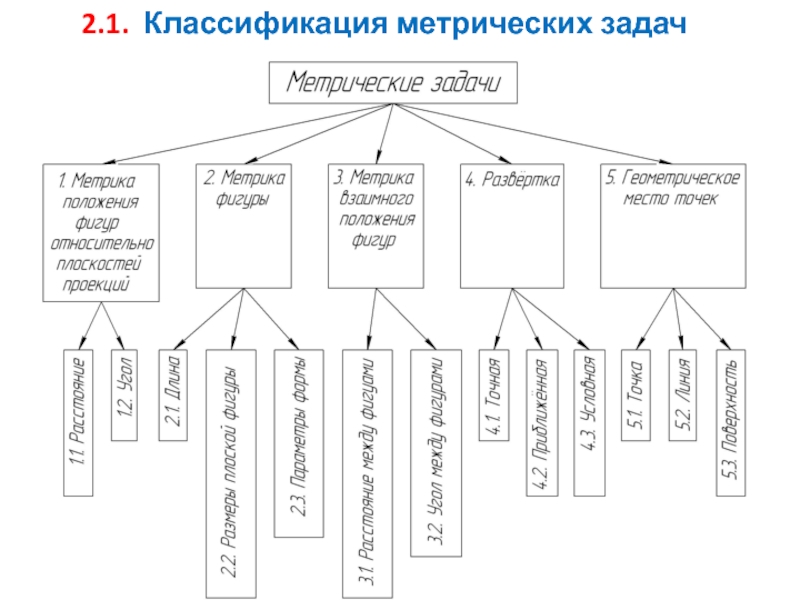
- 6. 2.1. Классификация метрических задач
- 7. 3. Проекции прямой 3.1. Прямая общего положения
- 8. Эпюр прямой по координатам: А(40,5,10),
- 9. 3.2. Прямые уровня Прямая параллельна одной из
- 10. Аксонометрия прямых уровня a) прямая ∥H –
- 11. Проекции прямых уровня на эпюре
- 12. Признаки по эпюру прямых уровня а) горизонтальная
- 13. Прямая, параллельная двум плоскостям проекций, будет перпендикулярна
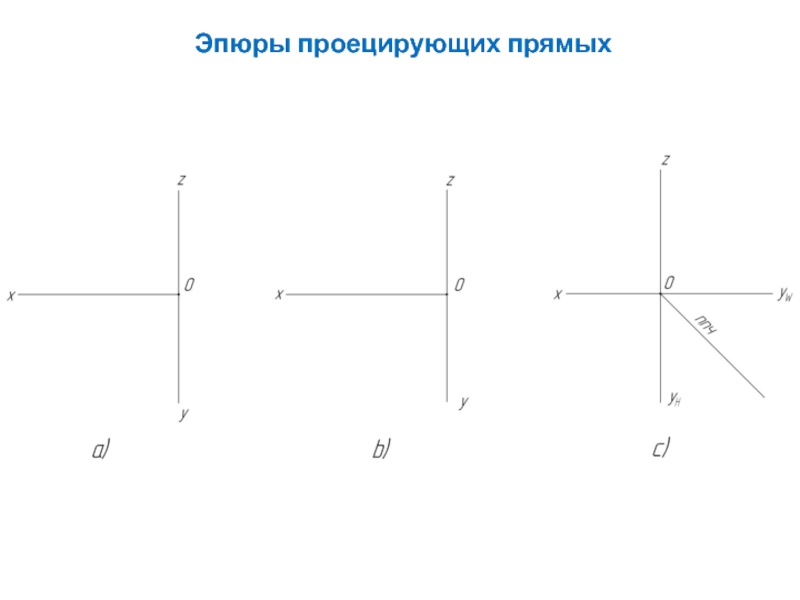
- 14. Эпюры проецирующих прямых
- 15. а) горизонтально-проецирующая прямая: для всех её точек
Слайд 21. Позиционные задачи
Задачи, в которых требуется определять положение фигуры относительно
Под взаимным положением фигур подразумевается их принадлежность, параллельность, пересечение, касание или непересечение.
Слайд 52. Метрические задачи
Задачи, в которых требуется определять:
метрические свойства данной фигуры
положения фигуры относительно плоскостей проекций или взаимного положения двух и более фигур называются метрическими
Слайд 73. Проекции прямой
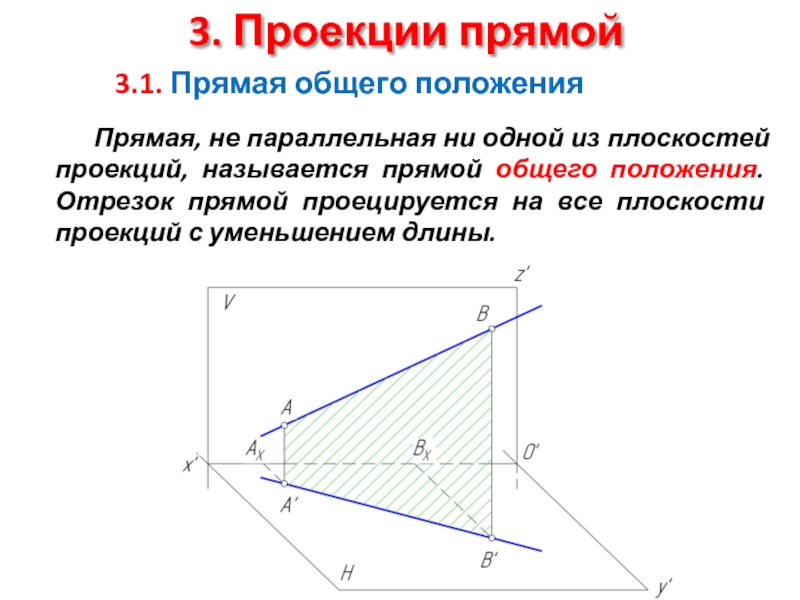
3.1. Прямая общего положения
Прямая, не параллельная ни одной из
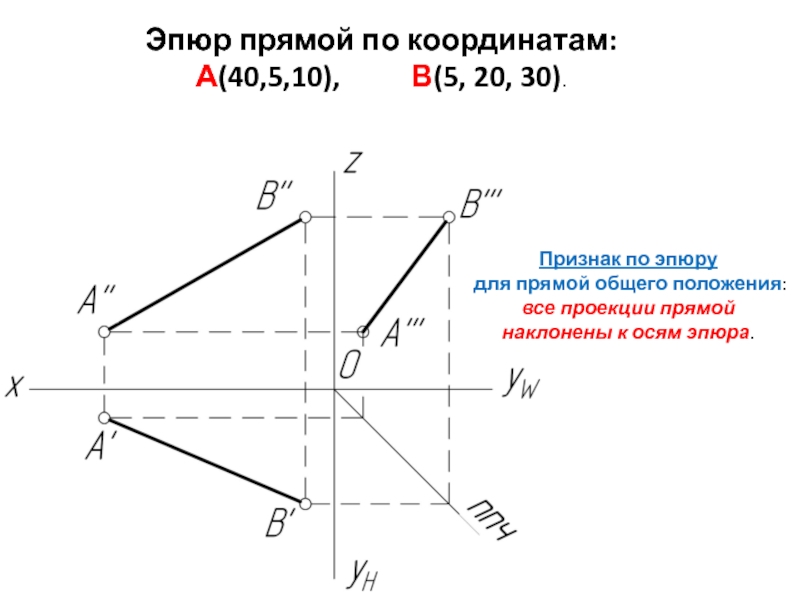
Слайд 8Эпюр прямой по координатам:
А(40,5,10), В(5, 20,
Признак по эпюру
для прямой общего положения:
все проекции прямой наклонены к осям эпюра.
Слайд 93.2. Прямые уровня
Прямая параллельна одной из плоскостей проекций
(H, V или
Общее название этих прямых – прямые уровня.
На эту плоскость отрезок прямой проецируется в истинную величину, а на две другие – с уменьшением.
На эту же плоскость проекций проецируются в истинную величину углы наклона прямой к двум другим плоскостям проекций!
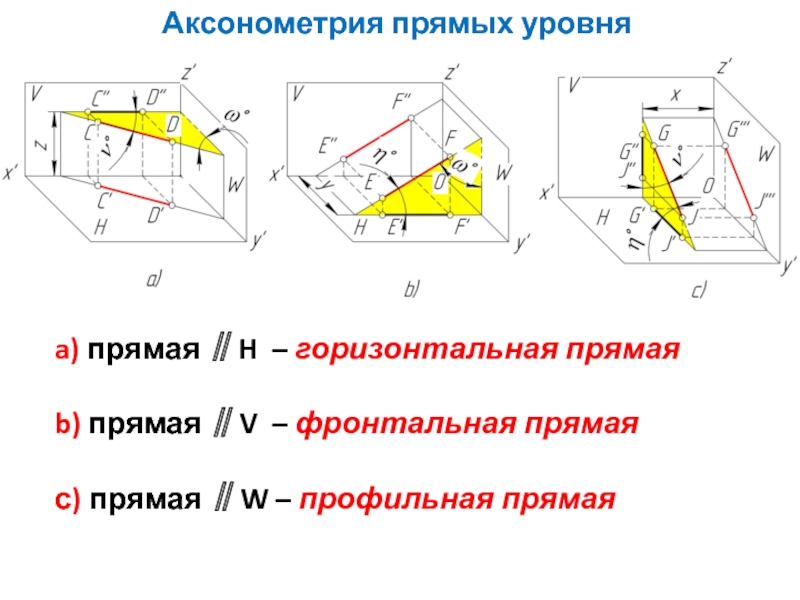
Слайд 10Аксонометрия прямых уровня
a) прямая ∥H – горизонтальная прямая
b) прямая ∥V –
с) прямая ∥W – профильная прямая
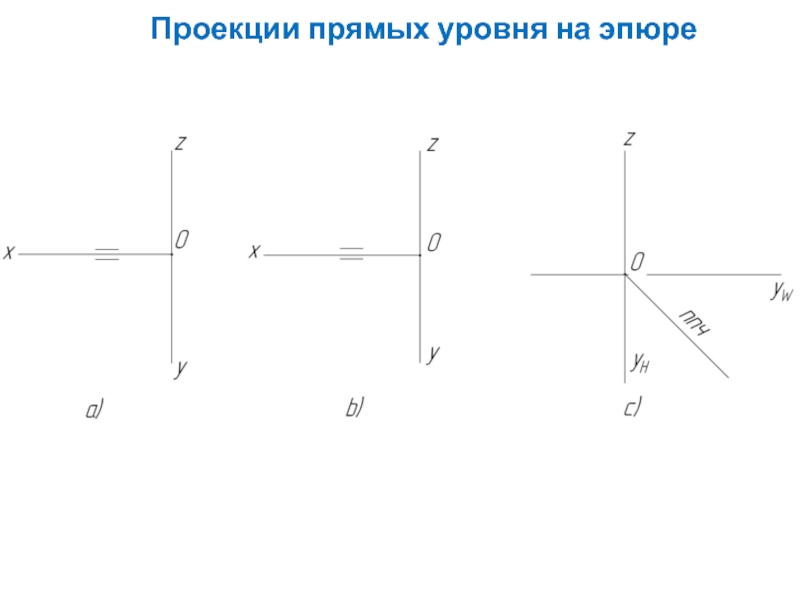
Слайд 12Признаки по эпюру прямых уровня
а) горизонтальная прямая. Признак по эпюру: фронтальная
b) фронтальная прямая. Признак по эпюру: горизонтальная проекция прямой оси х эпюра. ⏐EF⏐=⏐E''F''⏐, ν=00, η и ω - в истинную величину.
с) профильная прямая. Признак по эпюру: горизонтальная и фронтальная проекции прямой лежат на общей вертикальной линии связи.
⏐GJ⏐=⏐G'''J'''⏐, ω=00, η и ν - в истинную величину.
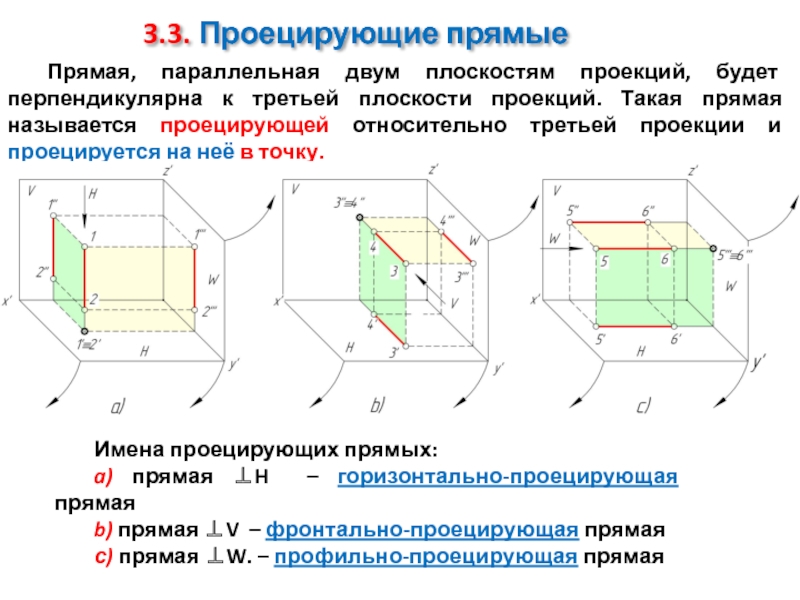
Слайд 13Прямая, параллельная двум плоскостям проекций, будет перпендикулярна к третьей плоскости проекций.
3.3. Проецирующие прямые
Имена проецирующих прямых:
a) прямая ⊥H – горизонтально-проецирующая прямая
b) прямая ⊥V – фронтально-проецирующая прямая
с) прямая ⊥W. – профильно-проецирующая прямая
Слайд 15а) горизонтально-проецирующая прямая: для всех её точек x=y=const, η=900, ⏐1-2⏐=⏐1''-2''⏐
b) фронтально-проецирующая
c) профильно-проецирующая прямая: для всех её точек y=z=const, ω=900, 5-6⏐=⏐5'-6'⏐=⏐5''-6''⏐
Относительно третьей плоскости проекций концы отрезков прямых являются конкурирующими, в смысле видимости: