Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол φ называется поворотом, или вращением. Прямая a при этом называется осью вращения.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поворот. Фигуры вращения презентация
Содержание
- 1. Поворот. Фигуры вращения
- 2. Упражнение 1 На какой угол нужно повернуть
- 3. Упражнение 2 На какой наименьший угол нужно
- 4. Упражнение 3 На какой наименьший угол нужно
- 5. Упражнение 4 На какой наименьший угол нужно
- 6. Упражнение 5 На какой наименьший угол нужно
- 7. Упражнение 6 На какой наименьший угол нужно
- 8. Упражнение 7 На какой наименьший угол нужно
- 9. Упражнение 8 На какой наименьший угол нужно
- 10. Упражнение 9 На какой наименьший угол нужно
- 11. Упражнение 10 На какой наименьший угол нужно
- 12. Упражнение 11 На какой наименьший угол нужно
- 13. Упражнение 12 На какой наименьший угол нужно
- 14. Упражнение 13 На какой наименьший угол нужно
- 15. Упражнение 14 На какой наименьший угол нужно
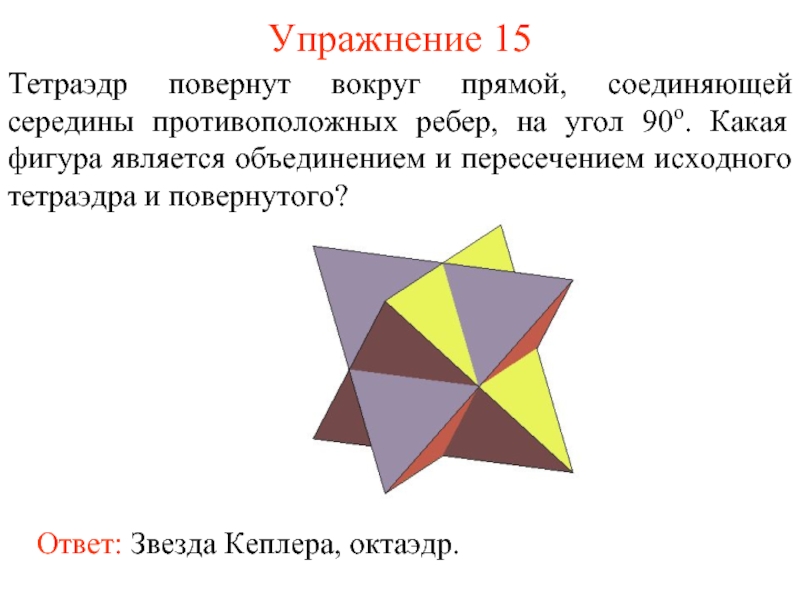
- 16. Упражнение 15 Тетраэдр повернут вокруг прямой, соединяющей
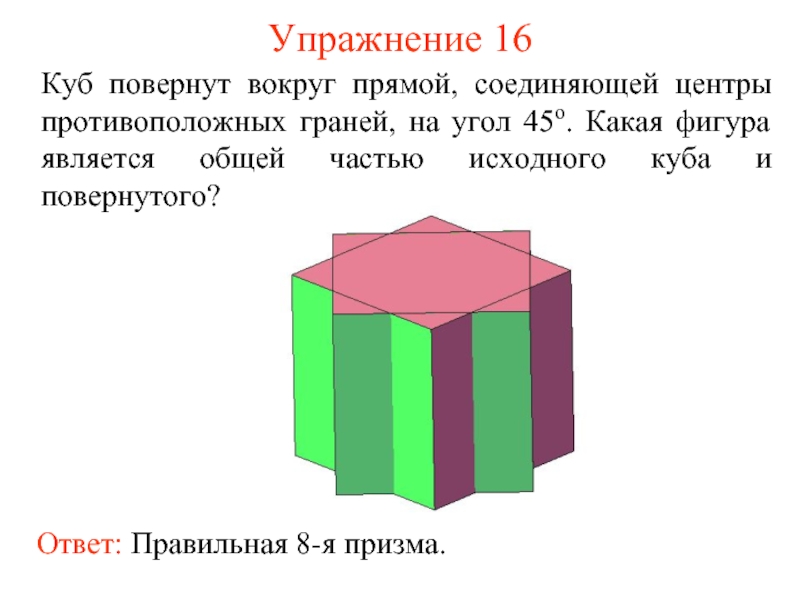
- 17. Упражнение 16 Куб повернут вокруг прямой, соединяющей
- 18. Упражнение 17 Куб повернут вокруг диагонали на
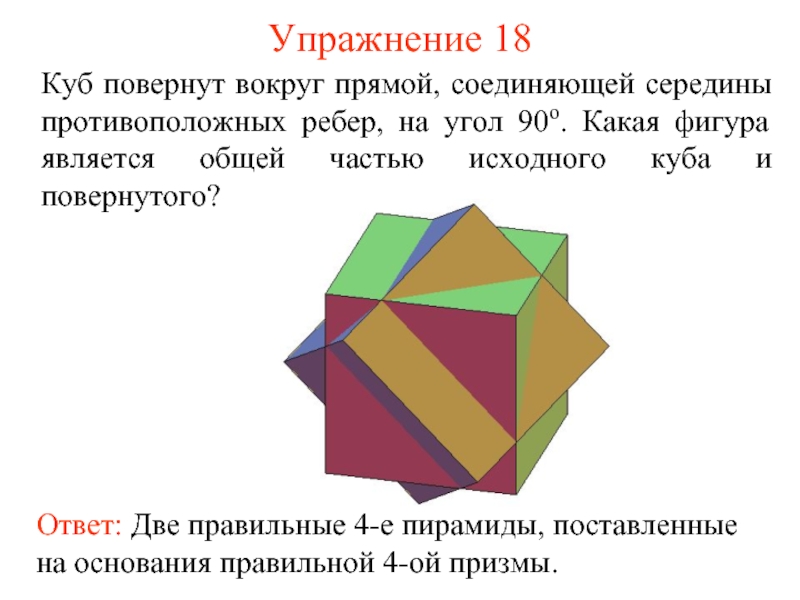
- 19. Упражнение 18 Куб повернут вокруг прямой, соединяющей
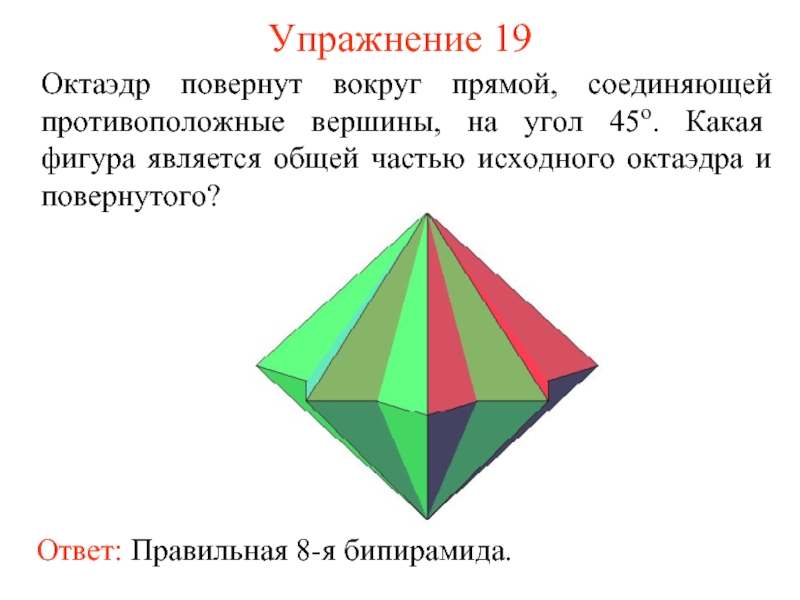
- 20. Упражнение 19 Октаэдр повернут вокруг прямой, соединяющей
- 21. Упражнение 20 Октаэдр повернут вокруг прямой, соединяющей
- 22. Упражнение 21 Икосаэдр повернут вокруг прямой, соединяющей
- 23. Упражнение 22 Додекаэдр повернут вокруг прямой, соединяющей
- 24. ФИГУРЫ ВРАЩЕНИЯ Говорят,что фигура
- 25. ФИГУРЫ ВРАЩЕНИЯ Цилиндр получается
- 26. ФИГУРЫ ВРАЩЕНИЯ Если окружность
- 27. ФИГУРЫ ВРАЩЕНИЯ При вращении
- 28. ФИГУРЫ ВРАЩЕНИЯ Если прямая
- 29. ГИПЕРБОЛОИД ВРАЩЕНИЯ Теорема. При
- 30. Упражнение 1 Какая фигура получается при вращении
- 31. Упражнение 2 Назовите прямые, при вращении вокруг
- 32. Упражнение 3 Какая фигура получается при вращении
- 33. Упражнение 4 Какая фигура получается при вращении полукруга вокруг прямой, содержащей диаметр? Ответ: Круг.
- 34. Упражнение 5 Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей его катет? Ответ: Конус.
- 35. Упражнение 6 Какая фигура получается вращением прямоугольного
- 36. Упражнение 7 Какая фигура получается вращением равнобедренного
- 37. Упражнение 8 Какая фигура получается вращением остроугольного
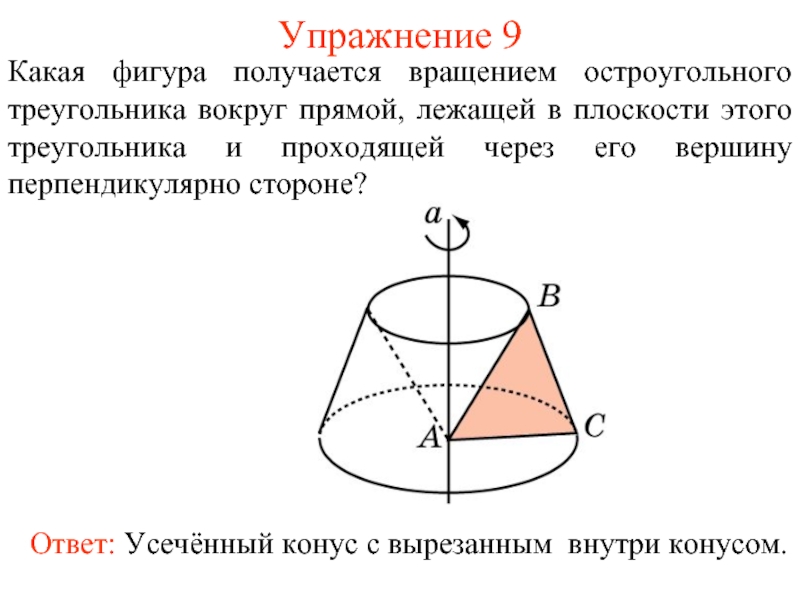
- 38. Упражнение 9 Какая фигура получается вращением остроугольного
- 39. Упражнение 10 Какая фигура получается вращением тупоугольного
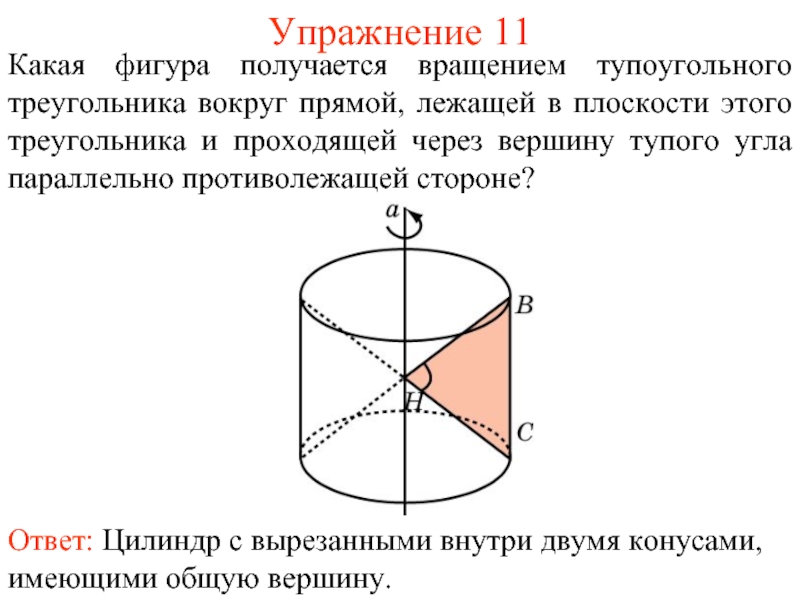
- 40. Упражнение 11 Какая фигура получается вращением тупоугольного
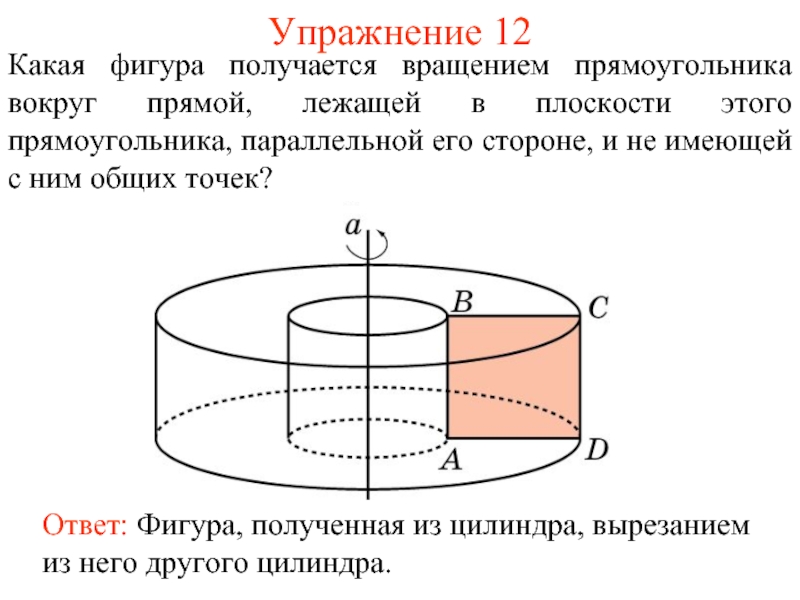
- 41. Упражнение 12 Какая фигура получается вращением прямоугольника
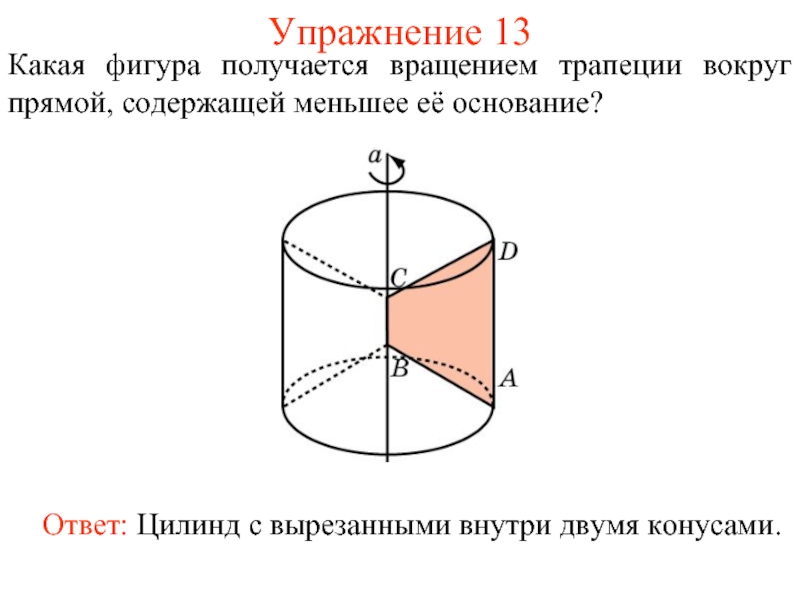
- 42. Упражнение 13 Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее её основание?
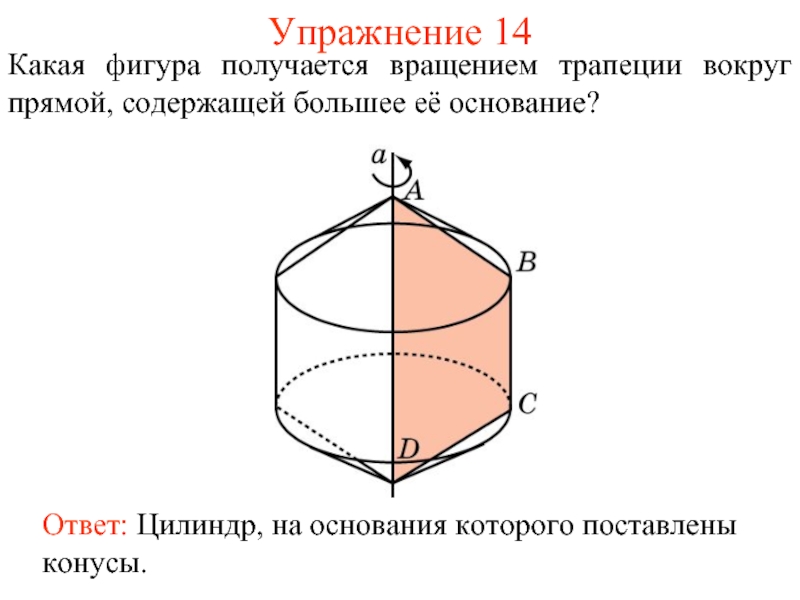
- 43. Упражнение 14 Какая фигура получается вращением трапеции вокруг прямой, содержащей большее её основание?
- 44. Упражнение 15 Вращением какой фигуры получается поверхность,
- 45. Упражнение 16 Какая фигура получается при вращении
- 46. Упражнение 17 Какая фигура получится при вращении
- 47. Упражнение 18 Какая фигура получается при вращении
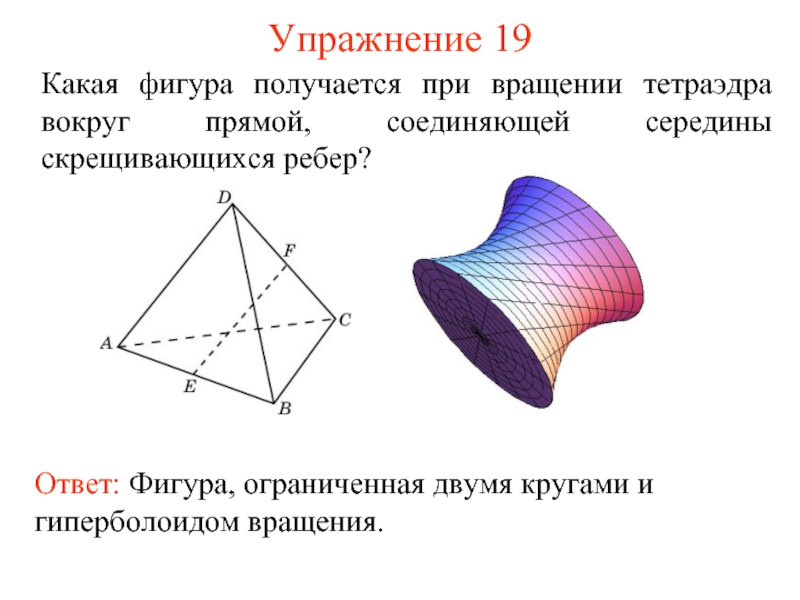
- 48. Упражнение 19 Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей середины скрещивающихся ребер?
- 49. Упражнение 20 Какая фигура
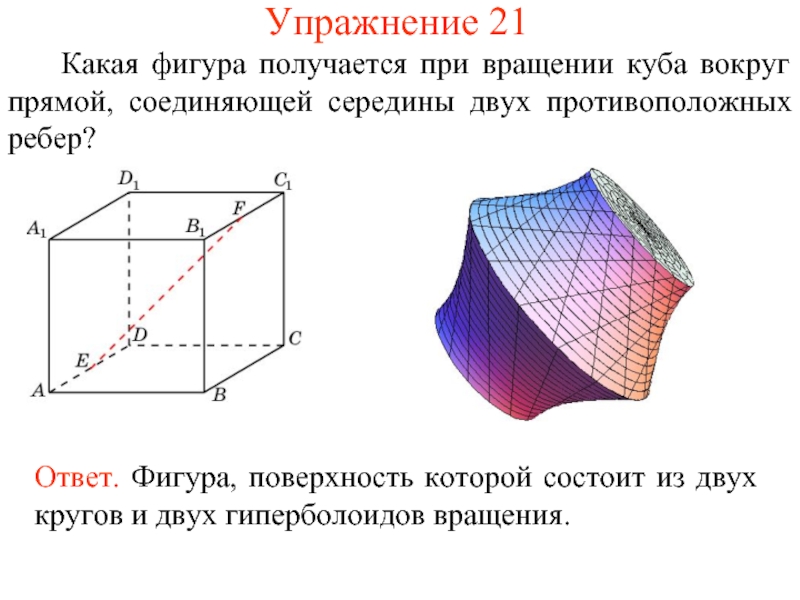
- 50. Упражнение 21 Какая фигура
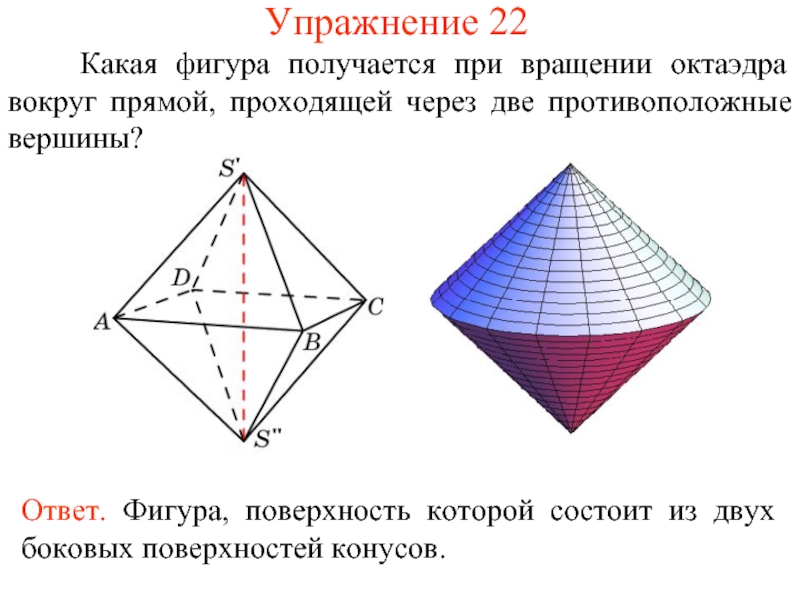
- 51. Упражнение 22 Какая фигура
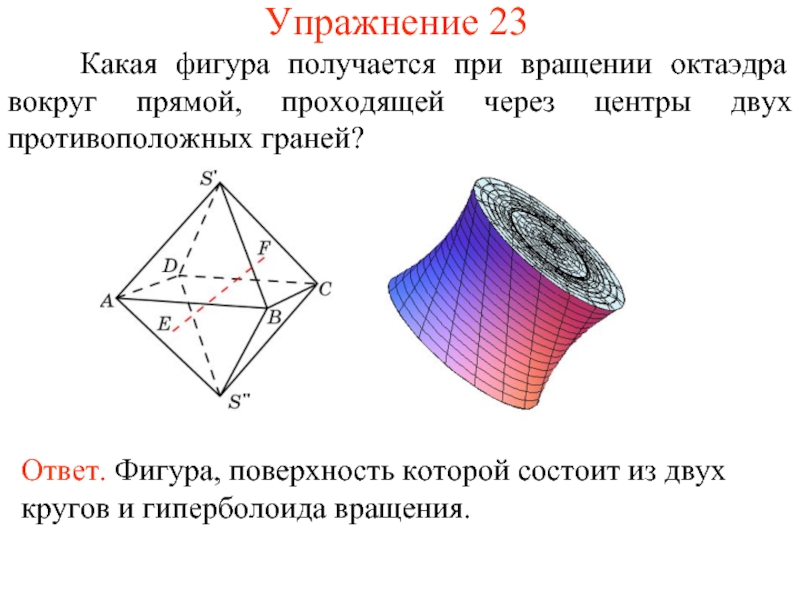
- 52. Упражнение 23 Какая фигура
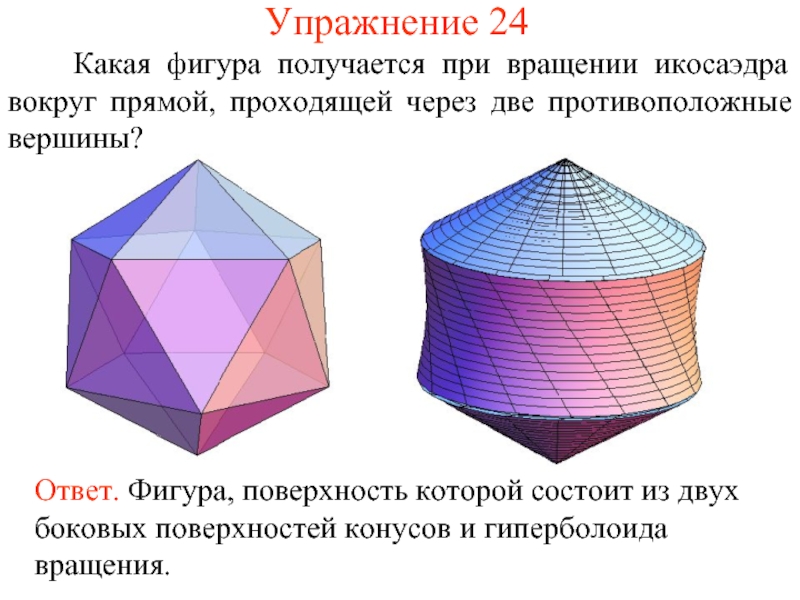
- 53. Упражнение 24 Какая фигура
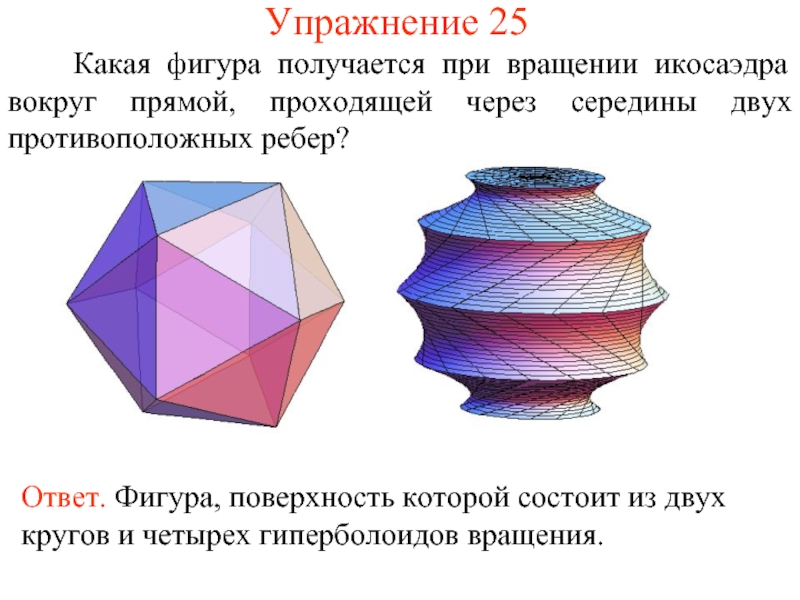
- 54. Упражнение 25 Какая фигура
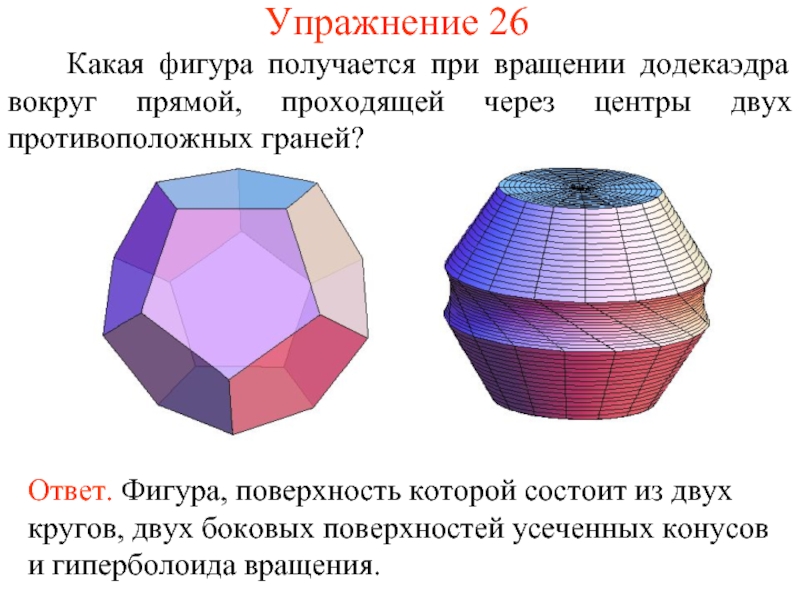
- 55. Упражнение 26 Какая фигура
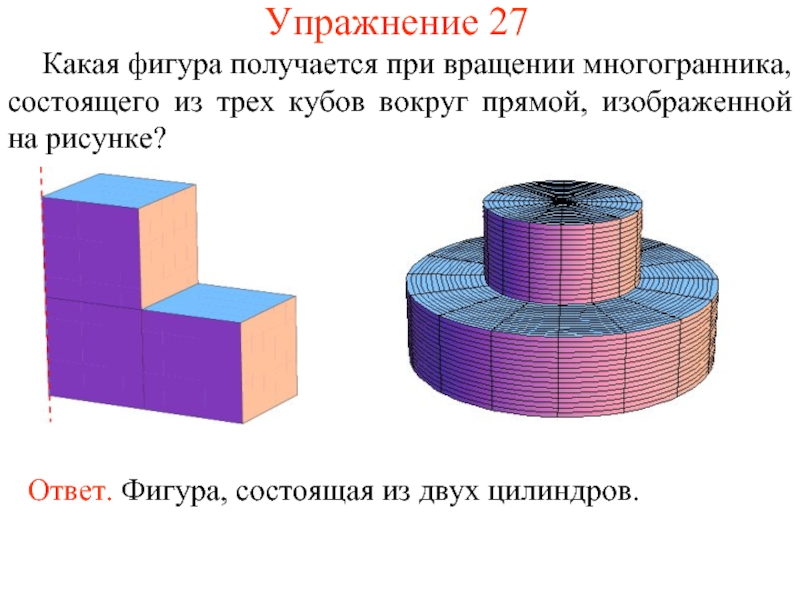
- 56. Упражнение 27 Какая фигура
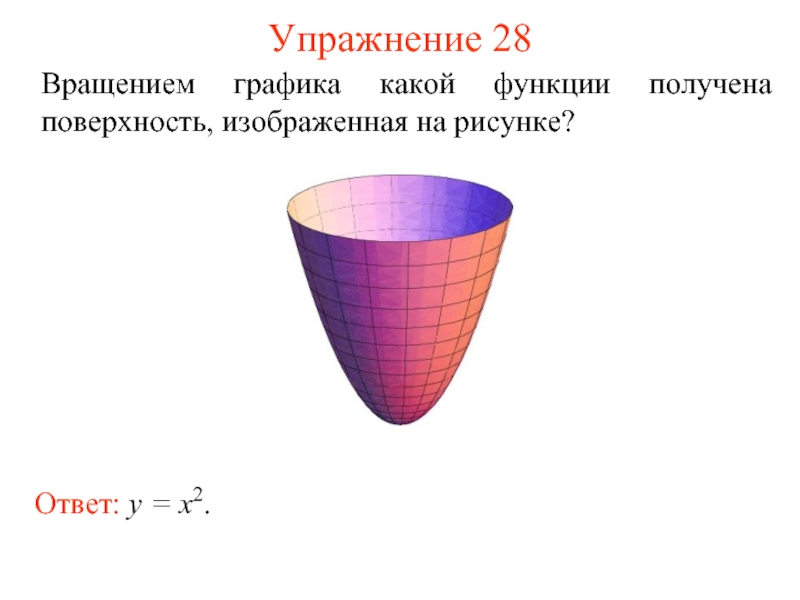
- 57. Упражнение 28 Вращением графика какой функции получена поверхность, изображенная на рисунке? Ответ: y = x2.
- 58. Упражнение 29 Вращением графика какой функции получена поверхность, изображенная на рисунке? Ответ: y = |x|.
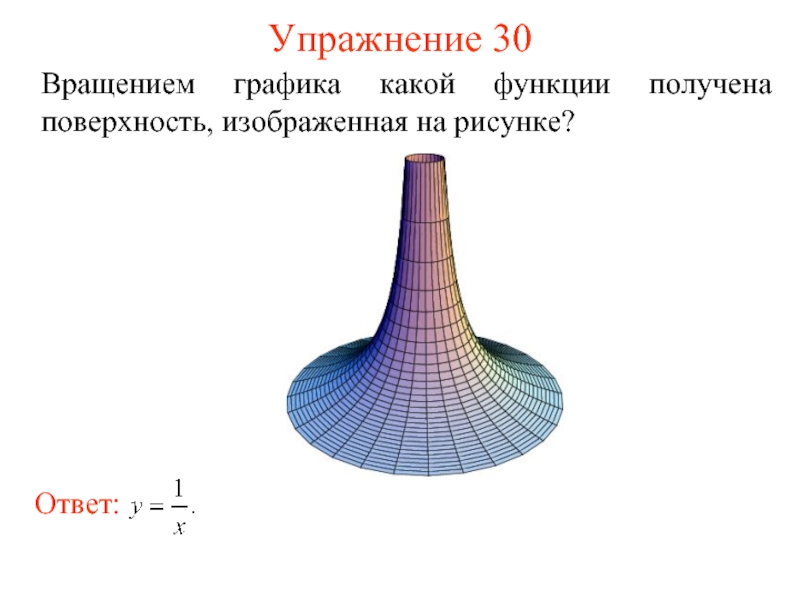
- 59. Упражнение 30 Вращением графика какой функции получена поверхность, изображенная на рисунке?
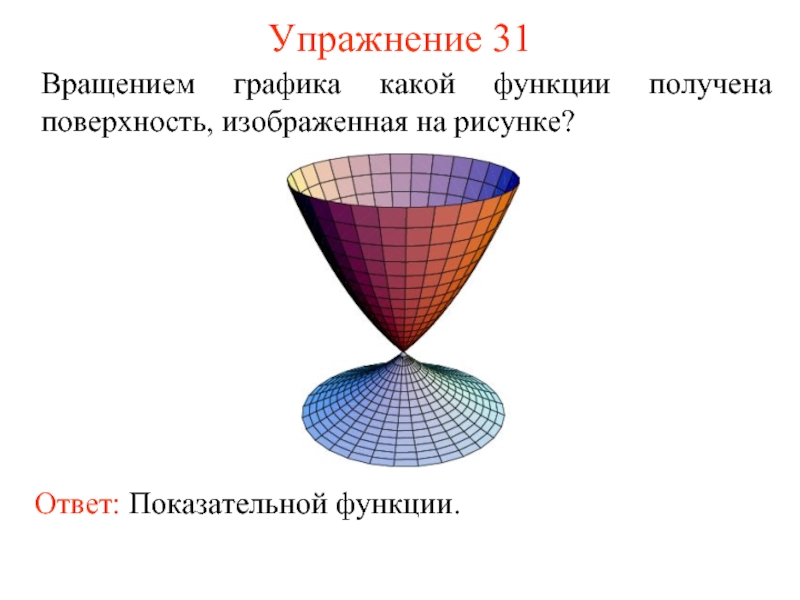
- 60. Упражнение 31 Вращением графика какой функции получена поверхность, изображенная на рисунке? Ответ: Показательной функции.
- 61. Упражнение 32 Вращением графика какой функции получена поверхность, изображенная на рисунке? Ответ: Синусоиды.
- 62. Упражнение 33 Вращением графика какой функции получена поверхность, изображенная на рисунке? Ответ: Косинусоиды.
- 63. Упражнение 34 Вращением графика какой функции получена
- 64. Упражнение 35 Вращением графика какой функции получена
- 65. Упражнение 36 Вращением графика какой функции получена
Упражнение 1 На какой угол нужно повернуть правильный тетраэдр вокруг прямой, проходящей через середины противоположных ребер, чтобы он совместился сам с собой? Ответ: 180о.
Слайд 1ПОВОРОТ
Пусть теперь в пространстве задана прямая a и
точка A, не принадлежащая этой прямой. Через точку A проведем плоскость α, перпендикулярную прямой a, и точку пересечения a и α обозначим O. Говорят, что точка A' пространства получается из точки A поворотом вокруг прямой a на угол φ, если в плоскости α точка A' получается из точки A поворотом вокруг центра O на угол φ.
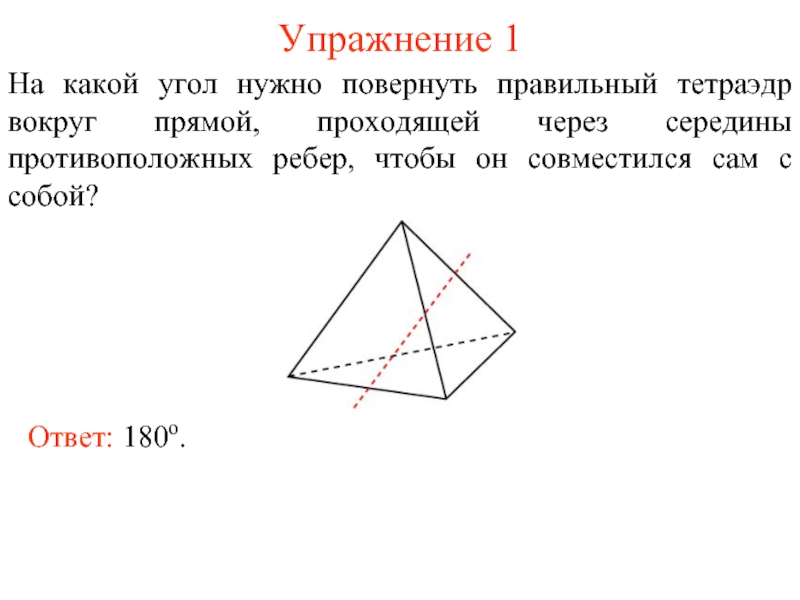
Слайд 2Упражнение 1
На какой угол нужно повернуть правильный тетраэдр вокруг прямой, проходящей
через середины противоположных ребер, чтобы он совместился сам с собой?
Ответ: 180о.
Слайд 3Упражнение 2
На какой наименьший угол нужно повернуть правильный тетраэдр вокруг прямой,
содержащей его высоту, чтобы он совместился сам с собой?
Ответ: 120о.
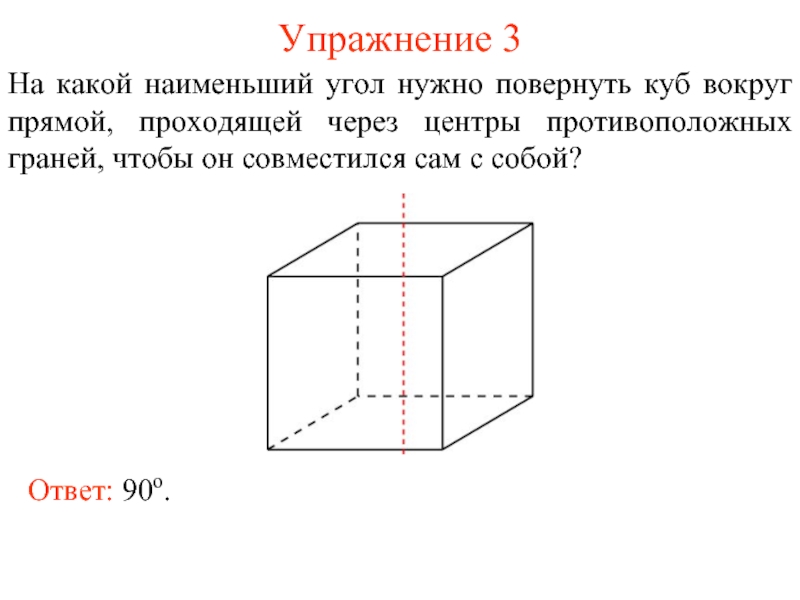
Слайд 4Упражнение 3
На какой наименьший угол нужно повернуть куб вокруг прямой, проходящей
через центры противоположных граней, чтобы он совместился сам с собой?
Ответ: 90о.
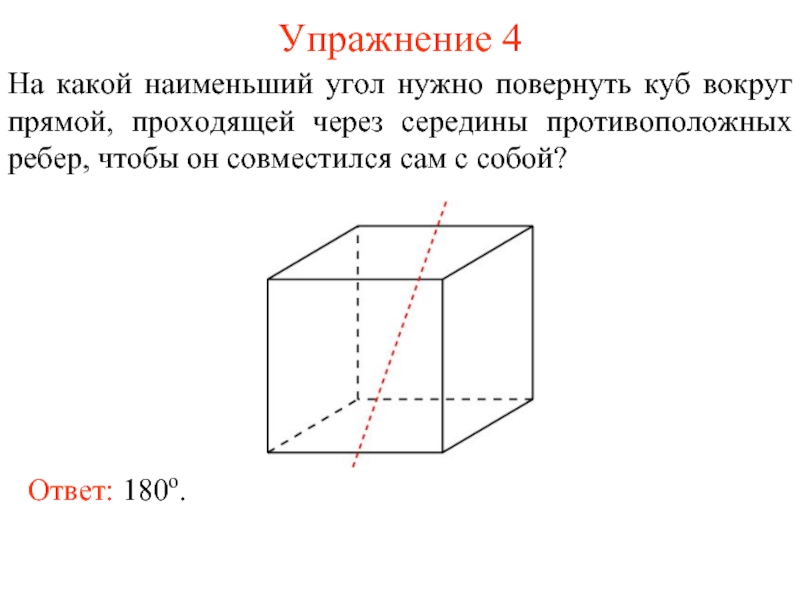
Слайд 5Упражнение 4
На какой наименьший угол нужно повернуть куб вокруг прямой, проходящей
через середины противоположных ребер, чтобы он совместился сам с собой?
Ответ: 180о.
Слайд 6Упражнение 5
На какой наименьший угол нужно повернуть куб вокруг прямой, проходящей
через противоположные вершины, чтобы он совместился сам с собой?
Ответ: 120о.
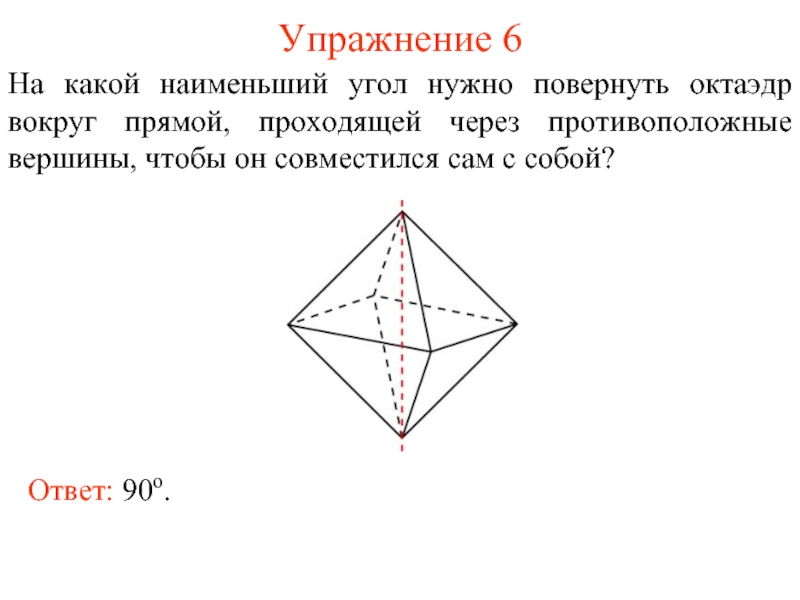
Слайд 7Упражнение 6
На какой наименьший угол нужно повернуть октаэдр вокруг прямой, проходящей
через противоположные вершины, чтобы он совместился сам с собой?
Ответ: 90о.
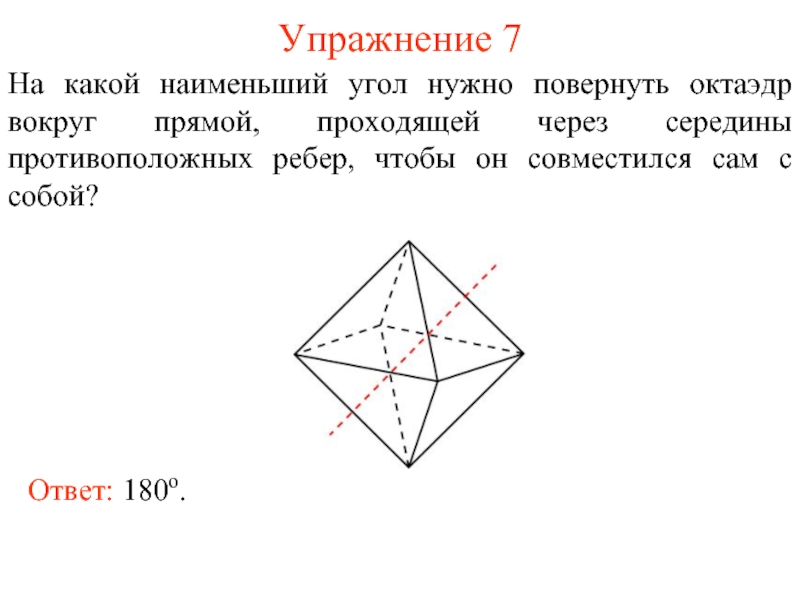
Слайд 8Упражнение 7
На какой наименьший угол нужно повернуть октаэдр вокруг прямой, проходящей
через середины противоположных ребер, чтобы он совместился сам с собой?
Ответ: 180о.
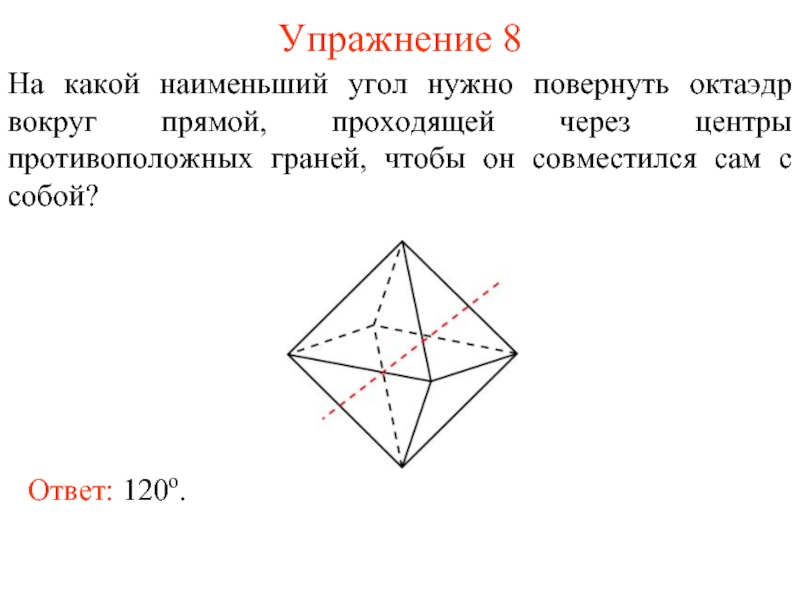
Слайд 9Упражнение 8
На какой наименьший угол нужно повернуть октаэдр вокруг прямой, проходящей
через центры противоположных граней, чтобы он совместился сам с собой?
Ответ: 120о.
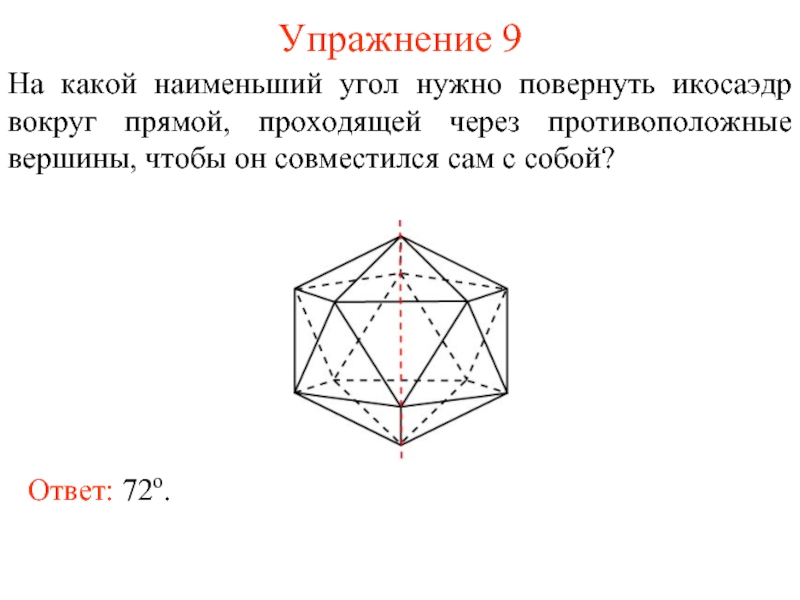
Слайд 10Упражнение 9
На какой наименьший угол нужно повернуть икосаэдр вокруг прямой, проходящей
через противоположные вершины, чтобы он совместился сам с собой?
Ответ: 72о.
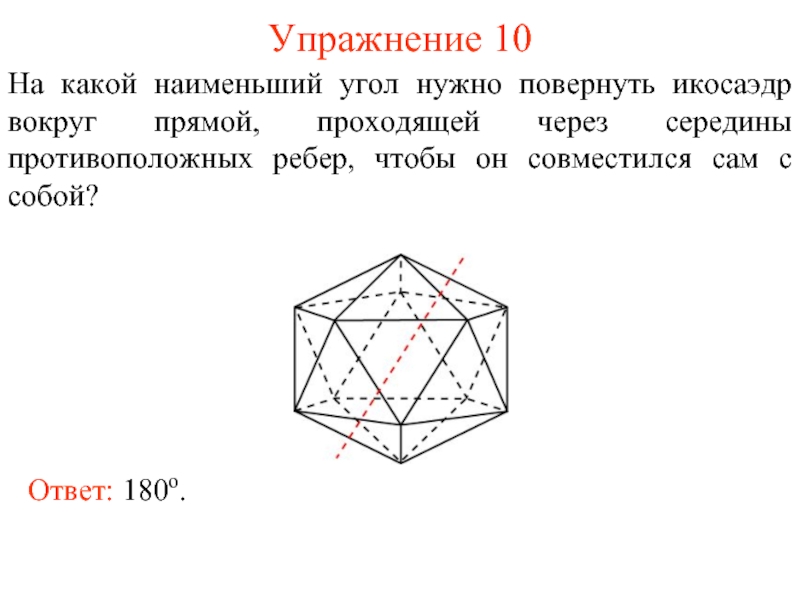
Слайд 11Упражнение 10
На какой наименьший угол нужно повернуть икосаэдр вокруг прямой, проходящей
через середины противоположных ребер, чтобы он совместился сам с собой?
Ответ: 180о.
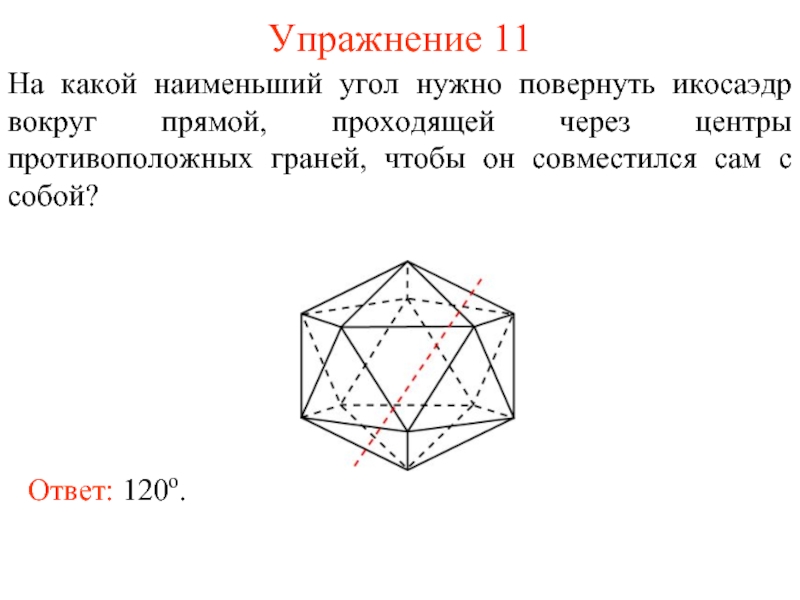
Слайд 12Упражнение 11
На какой наименьший угол нужно повернуть икосаэдр вокруг прямой, проходящей
через центры противоположных граней, чтобы он совместился сам с собой?
Ответ: 120о.
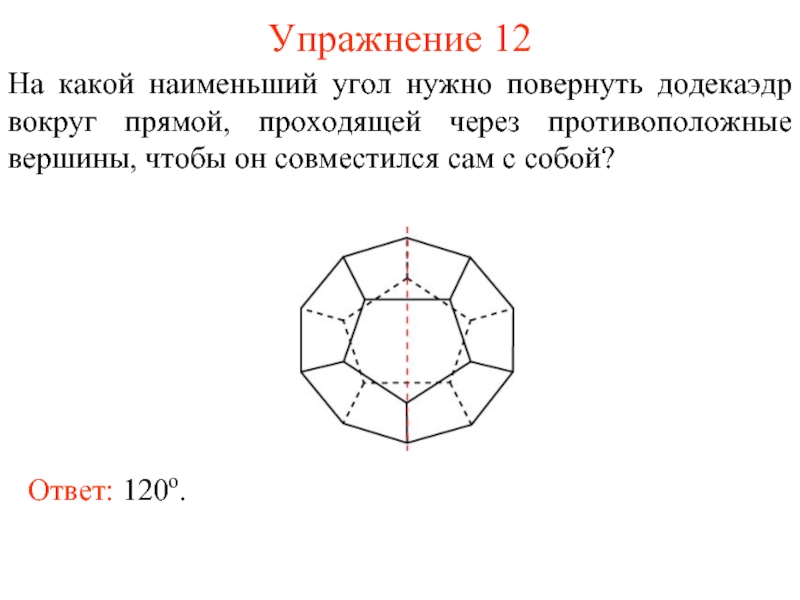
Слайд 13Упражнение 12
На какой наименьший угол нужно повернуть додекаэдр вокруг прямой, проходящей
через противоположные вершины, чтобы он совместился сам с собой?
Ответ: 120о.
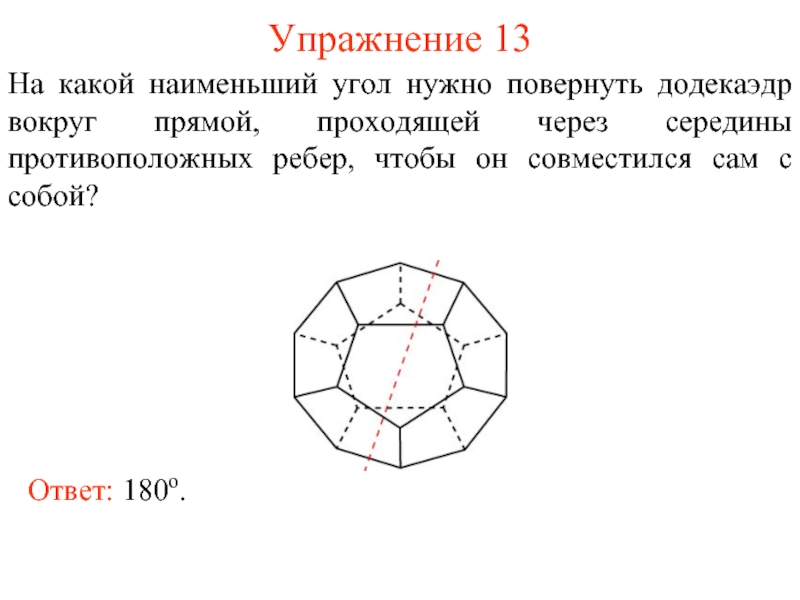
Слайд 14Упражнение 13
На какой наименьший угол нужно повернуть додекаэдр вокруг прямой, проходящей
через середины противоположных ребер, чтобы он совместился сам с собой?
Ответ: 180о.
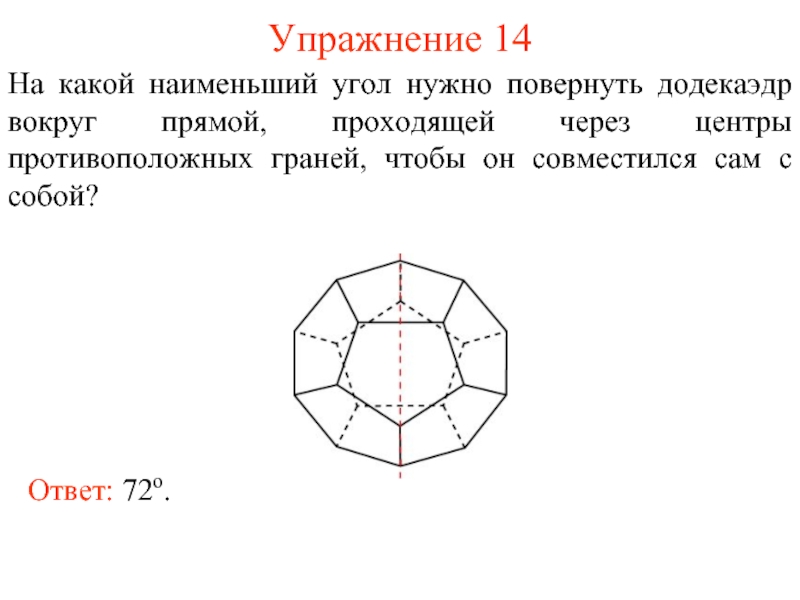
Слайд 15Упражнение 14
На какой наименьший угол нужно повернуть додекаэдр вокруг прямой, проходящей
через центры противоположных граней, чтобы он совместился сам с собой?
Ответ: 72о.
Слайд 16Упражнение 15
Тетраэдр повернут вокруг прямой, соединяющей середины противоположных ребер, на угол
90о. Какая фигура является объединением и пересечением исходного тетраэдра и повернутого?
Слайд 17Упражнение 16
Куб повернут вокруг прямой, соединяющей центры противоположных граней, на угол
45о. Какая фигура является общей частью исходного куба и повернутого?
Слайд 18Упражнение 17
Куб повернут вокруг диагонали на угол 60о. Какая фигура является
общей частью исходного куба и повернутого?
Слайд 19Упражнение 18
Куб повернут вокруг прямой, соединяющей середины противоположных ребер, на угол
90о. Какая фигура является общей частью исходного куба и повернутого?
Слайд 20Упражнение 19
Октаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол 45о.
Какая фигура является общей частью исходного октаэдра и повернутого?
Слайд 21Упражнение 20
Октаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на угол
60о. Какая фигура является общей частью исходного октаэдра и повернутого?
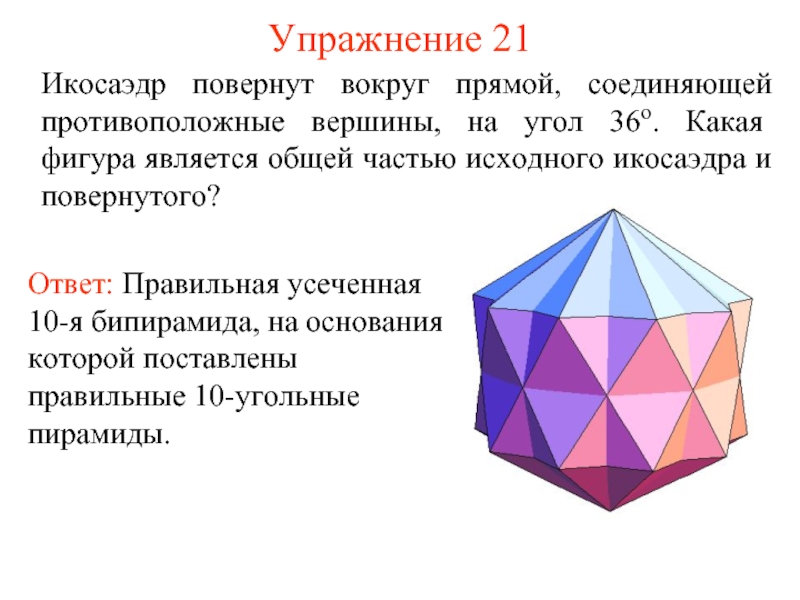
Слайд 22Упражнение 21
Икосаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол 36о.
Какая фигура является общей частью исходного икосаэдра и повернутого?
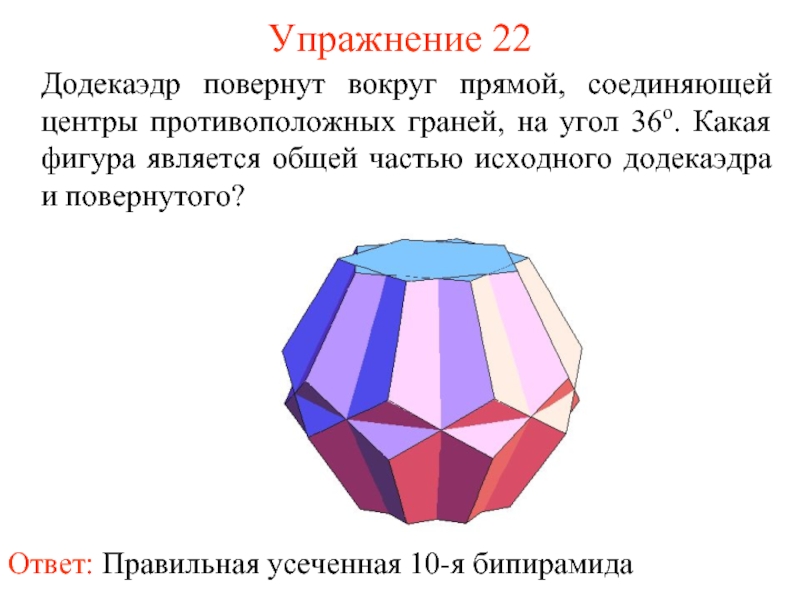
Слайд 23Упражнение 22
Додекаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на угол
36о. Какая фигура является общей частью исходного додекаэдра и повернутого?
Слайд 24ФИГУРЫ ВРАЩЕНИЯ
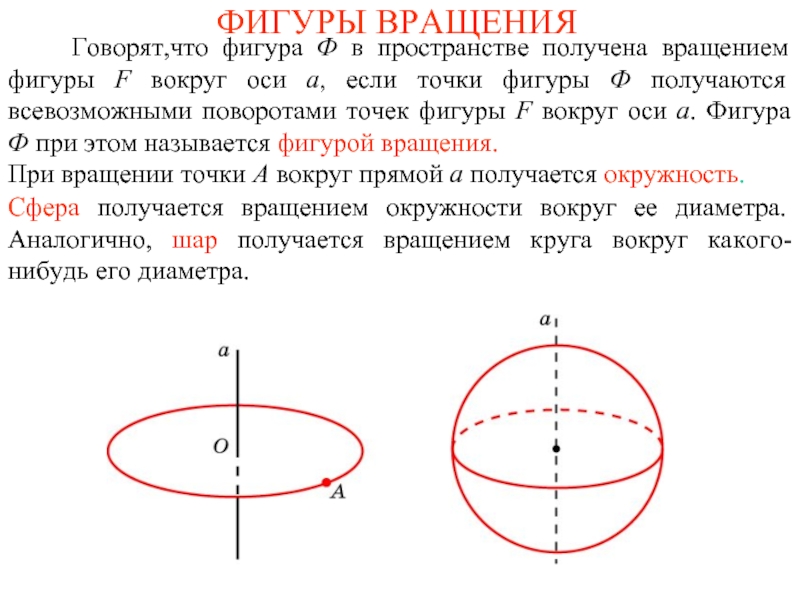
Говорят,что фигура Ф в пространстве получена вращением
фигуры F вокруг оси a, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.
При вращении точки A вокруг прямой a получается окружность.
Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.
Слайд 25ФИГУРЫ ВРАЩЕНИЯ
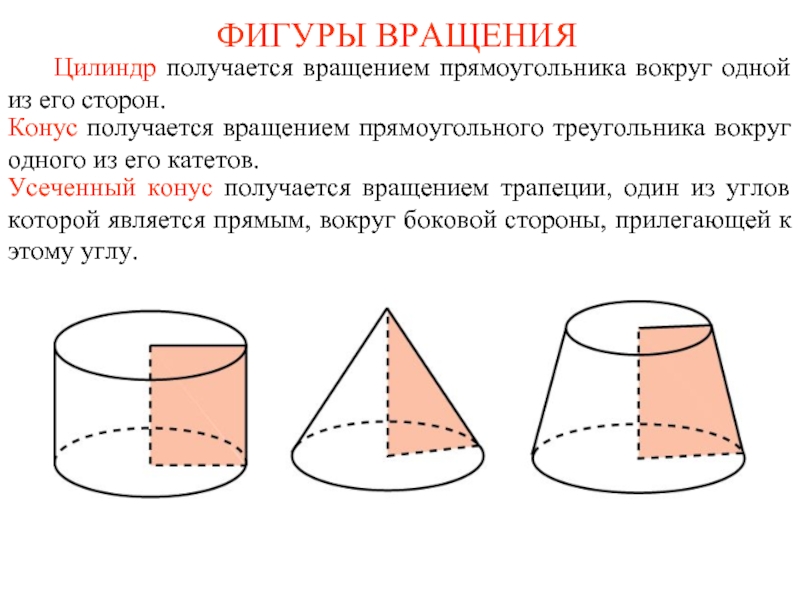
Цилиндр получается вращением прямоугольника вокруг одной из
его сторон.
Конус получается вращением прямоугольного треугольника вокруг одного из его катетов.
Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу.
Слайд 26ФИГУРЫ ВРАЩЕНИЯ
Если окружность вращать вокруг прямой, лежащей в
плоскости окружности и не имеющей с этой окружностью общих точек, то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик.
При вращении эллипса вокруг его оси получается поверхность, называемая эллипсоидом вращения.
Слайд 27ФИГУРЫ ВРАЩЕНИЯ
При вращении параболы вокруг ее оси получается
поверхность, называемая параболоидом вращения.
При вращении гиперболы вокруг ее оси получается поверхность, называемая гиперболоидом вращения.
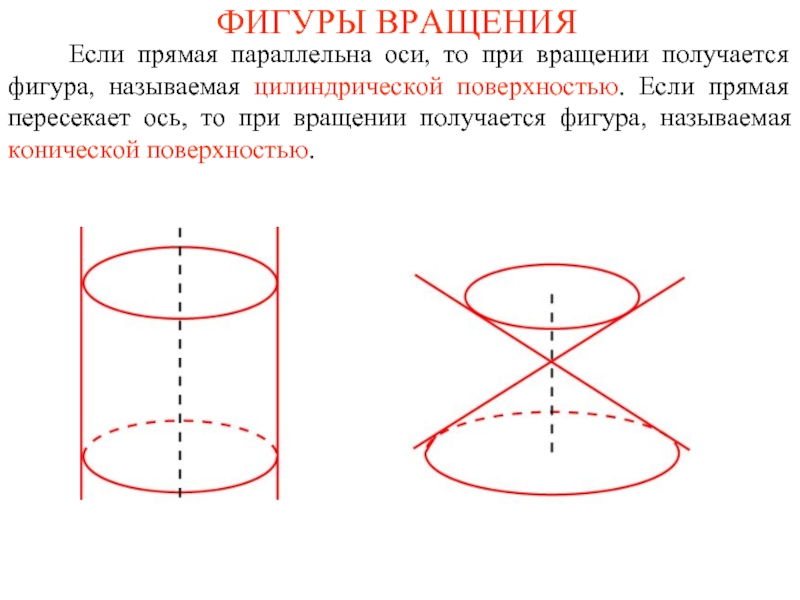
Слайд 28ФИГУРЫ ВРАЩЕНИЯ
Если прямая параллельна оси, то при вращении
получается фигура, называемая цилиндрической поверхностью. Если прямая пересекает ось, то при вращении получается фигура, называемая конической поверхностью.
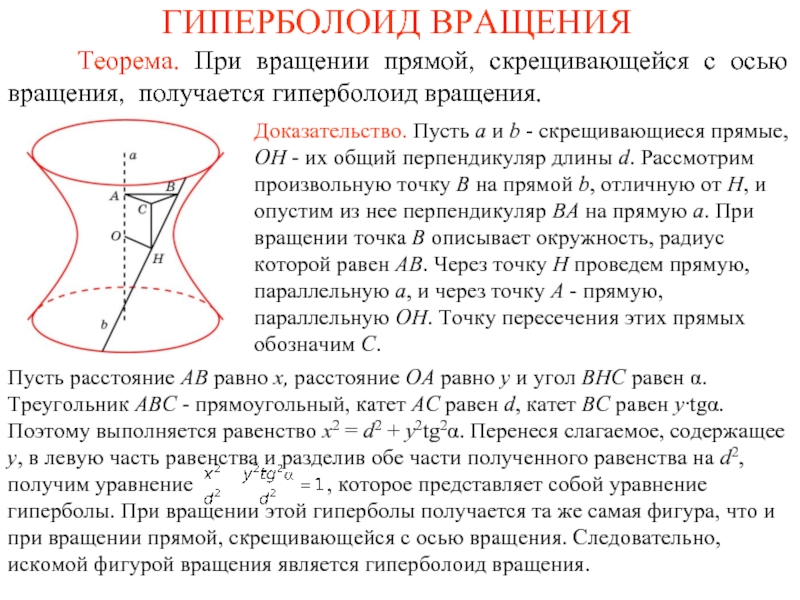
Слайд 29ГИПЕРБОЛОИД ВРАЩЕНИЯ
Теорема. При вращении прямой, скрещивающейся с осью
вращения, получается гиперболоид вращения.
Доказательство. Пусть a и b - скрещивающиеся прямые, OH - их общий перпендикуляр длины d. Рассмотрим произвольную точку B на прямой b, отличную от H, и опустим из нее перпендикуляр BA на прямую a. При вращении точка B описывает окружность, радиус которой равен AB. Через точку H проведем прямую, параллельную a, и через точку A - прямую, параллельную OH. Точку пересечения этих прямых обозначим C.
Пусть расстояние AB равно x, расстояние OA равно y и угол BHC равен α. Треугольник ABC - прямоугольный, катет AC равен d, катет BC равен y·tgα. Поэтому выполняется равенство x2 = d2 + y2tg2α. Перенеся слагаемое, содержащее y, в левую часть равенства и разделив обе части полученного равенства на d2, получим уравнение , которое представляет собой уравнение гиперболы. При вращении этой гиперболы получается та же самая фигура, что и при вращении прямой, скрещивающейся с осью вращения. Следовательно, искомой фигурой вращения является гиперболоид вращения.
Слайд 30Упражнение 1
Какая фигура получается при вращении отрезка OA вокруг прямой, проходящей
через точку O и перпендикулярной OA?
Ответ: Круг.
Слайд 31Упражнение 2
Назовите прямые, при вращении вокруг которых данного прямоугольника получается цилиндр.
Ответ:
Прямые, пересекающие прямоугольник по отрезку, параллельному его стороне.
Слайд 32Упражнение 3
Какая фигура получается при вращении равнобедренного треугольника вокруг прямой, содержащей
высоту, опущенную на основание этого треугольника?
Ответ: Конус.
Слайд 33Упражнение 4
Какая фигура получается при вращении полукруга вокруг прямой, содержащей диаметр?
Ответ:
Круг.
Слайд 34Упражнение 5
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей его
катет?
Ответ: Конус.
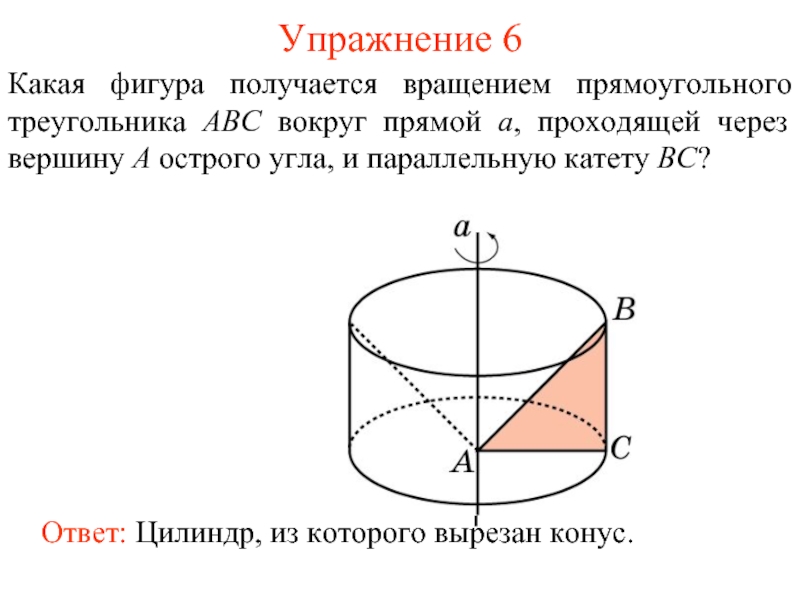
Слайд 35Упражнение 6
Какая фигура получается вращением прямоугольного треугольника ABC вокруг прямой a,
проходящей через вершину A острого угла, и параллельную катету BC?
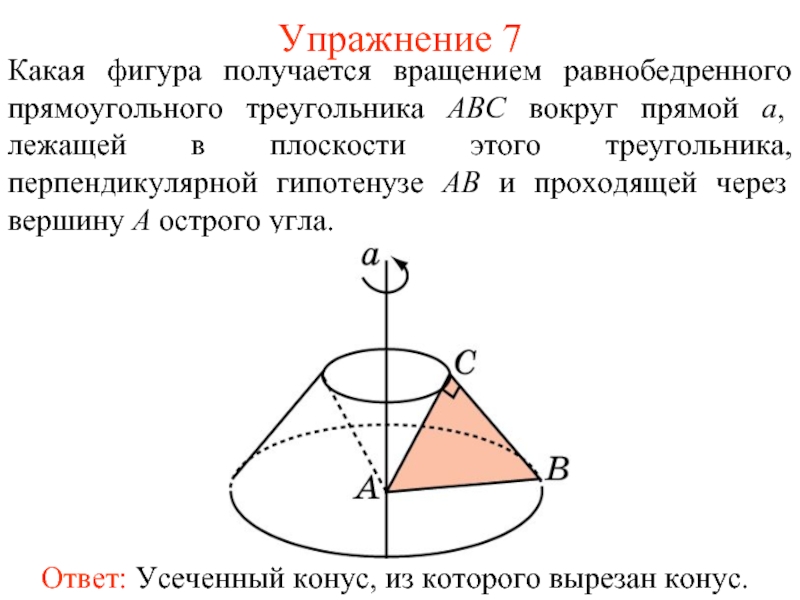
Слайд 36Упражнение 7
Какая фигура получается вращением равнобедренного прямоугольного треугольника ABC вокруг прямой
a, лежащей в плоскости этого треугольника, перпендикулярной гипотенузе AB и проходящей через вершину A острого угла.
Слайд 37Упражнение 8
Какая фигура получается вращением остроугольного треугольника вокруг прямой, содержащей его
сторону?
Ответ: Фигура, состоящая из двух конусов с общим основанием.
Слайд 38Упражнение 9
Какая фигура получается вращением остроугольного треугольника вокруг прямой, лежащей в
плоскости этого треугольника и проходящей через его вершину перпендикулярно стороне?
Слайд 39Упражнение 10
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, содержащей его
сторону, прилегающую к тупому углу?
Ответ: Фигура, полученная из конуса, вырезанием из него другого конуса.
Слайд 40Упражнение 11
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, лежащей в
плоскости этого треугольника и проходящей через вершину тупого угла параллельно противолежащей стороне?
Ответ: Цилиндр с вырезанными внутри двумя конусами, имеющими общую вершину.
Слайд 41Упражнение 12
Какая фигура получается вращением прямоугольника вокруг прямой, лежащей в плоскости
этого прямоугольника, параллельной его стороне, и не имеющей с ним общих точек?
Слайд 42Упражнение 13
Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее её
основание?
Слайд 43Упражнение 14
Какая фигура получается вращением трапеции вокруг прямой, содержащей большее её
основание?
Слайд 44Упражнение 15
Вращением какой фигуры получается поверхность, изображенная на рисунке, называемая тором.
Ответ: Вращением окружности вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек.
Слайд 45Упражнение 16
Какая фигура получается при вращении куба вокруг прямой, соединяющей центры
противоположных граней.
Ответ: Цилиндр.
Слайд 46Упражнение 17
Какая фигура получится при вращении правильной n-угольной призмы вокруг прямой,
проходящей через центры ее оснований?
Ответ: Цилиндр.
Слайд 47Упражнение 18
Какая фигура получается при вращении правильной n-угольной пирамиды вокруг прямой,
содержащей ее высоту?
Ответ: Конус.
Слайд 48Упражнение 19
Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей середины
скрещивающихся ребер?
Слайд 49Упражнение 20
Какая фигура получается при вращении куба вокруг
прямой, содержащей его диагональ?
Слайд 50Упражнение 21
Какая фигура получается при вращении куба вокруг
прямой, соединяющей середины двух противоположных ребер?
Слайд 51Упражнение 22
Какая фигура получается при вращении октаэдра вокруг
прямой, проходящей через две противоположные вершины?
Слайд 52Упражнение 23
Какая фигура получается при вращении октаэдра вокруг
прямой, проходящей через центры двух противоположных граней?
Слайд 53Упражнение 24
Какая фигура получается при вращении икосаэдра вокруг
прямой, проходящей через две противоположные вершины?
Слайд 54Упражнение 25
Какая фигура получается при вращении икосаэдра вокруг
прямой, проходящей через середины двух противоположных ребер?
Слайд 55Упражнение 26
Какая фигура получается при вращении додекаэдра вокруг
прямой, проходящей через центры двух противоположных граней?
Слайд 56Упражнение 27
Какая фигура получается при вращении многогранника, состоящего
из трех кубов вокруг прямой, изображенной на рисунке?
Слайд 57Упражнение 28
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: y
= x2.
Слайд 58Упражнение 29
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: y
= |x|.
Слайд 60Упражнение 31
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Показательной
функции.
Слайд 61Упражнение 32
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Синусоиды.
Слайд 62Упражнение 33
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: Косинусоиды.
Слайд 63Упражнение 34
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: y
= sin x.
Слайд 64Упражнение 35
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: y
= tg x.
Слайд 65Упражнение 36
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Ответ: y
= arcsin x.
