- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхностные интегралы презентация
Содержание
- 1. Поверхностные интегралы
- 2. 20.1. ПОНЯТИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА Понятие двойного
- 3. Сумму вида называют интегральной суммой для функции f(x,y,z) по поверхности S.
- 4. Если существует конечный предел интегральной суммы
- 5. Свойства поверхностных интегралов аналогичны свойствам двойных интегралов.
- 7. Выберем элемент площади dxdy плоскости D и
- 8. Тогда
20.1. ПОНЯТИЕ ПОВЕРХНОСТНОГО
ИНТЕГРАЛА Понятие двойного интеграла по плоской области обобщается на случай интегрирования по поверхности. Пусть S – некоторая поверхность, f(x,y,z) – непрерывная функция на поверхности S. Разобьем поверхность
Слайд 220.1. ПОНЯТИЕ ПОВЕРХНОСТНОГО
ИНТЕГРАЛА
Понятие двойного интеграла по плоской области обобщается на
случай интегрирования по поверхности.
Пусть S – некоторая поверхность, f(x,y,z) – непрерывная функция на поверхности S.
Разобьем поверхность S на части с площадями ΔGi. На каждой части выберем точку
Пусть S – некоторая поверхность, f(x,y,z) – непрерывная функция на поверхности S.
Разобьем поверхность S на части с площадями ΔGi. На каждой части выберем точку
Слайд 4
Если существует конечный предел интегральной суммы при стремлении к 0 диаметра
каждой площадки разбиения, не зависящий от способа разбиения поверхности S и выбора точек (xi,yi,zi), то он называется интегралом по поверхности S от функции f(x,у,z).
Слайд 5Свойства поверхностных интегралов аналогичны свойствам двойных интегралов.
Рассмотрим вычисление поверхностных интегралов.
Пусть дан
поверхностный интеграл
и поверхность S задана уравнением z=z(x,y).
В этом случае вычисление поверхностного интеграла сведется к вычислению двойного интеграла по области D – проекции поверхности S на плоскость ХОУ.
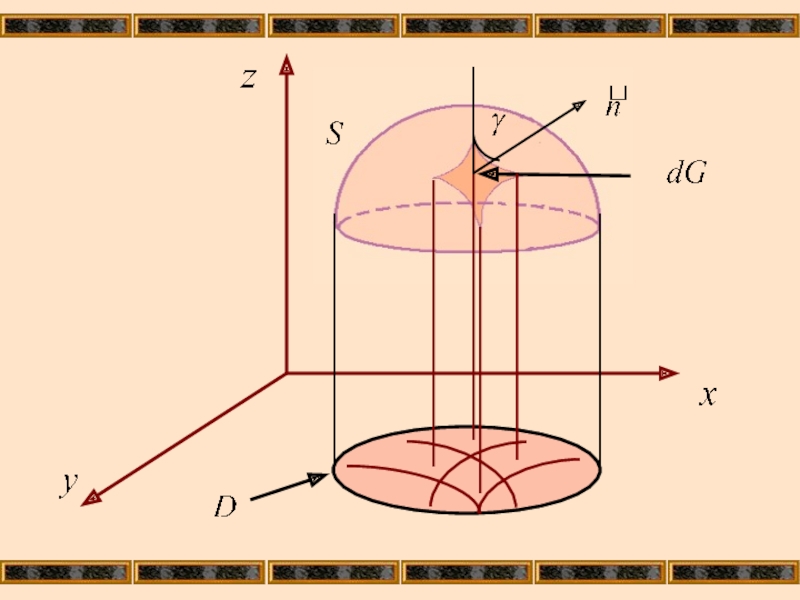
Слайд 7Выберем элемент площади dxdy плоскости D и проектирующийся в него элемент
площади ΔG поверхности S.
Проведем нормаль к ΔG так, чтобы она образовывала острый угол γ с oz.
Тогда
Проведем нормаль к ΔG так, чтобы она образовывала острый угол γ с oz.
Тогда
Нормаль к поверхности z=z(x,y) имеет проекции
