- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности второго порядка презентация
Содержание
- 1. Поверхности второго порядка
- 2. Лекция 9 2. Исследование формы поверхностей второго
- 3. F(x,y,z) = 0,
- 4. Алгебраической поверхностью второго порядка называется поверхность ,
- 5. Всякое уравнение (2), задающее невырожденную поверхность ,
- 6. Исследование формы поверхностей второго порядка по их
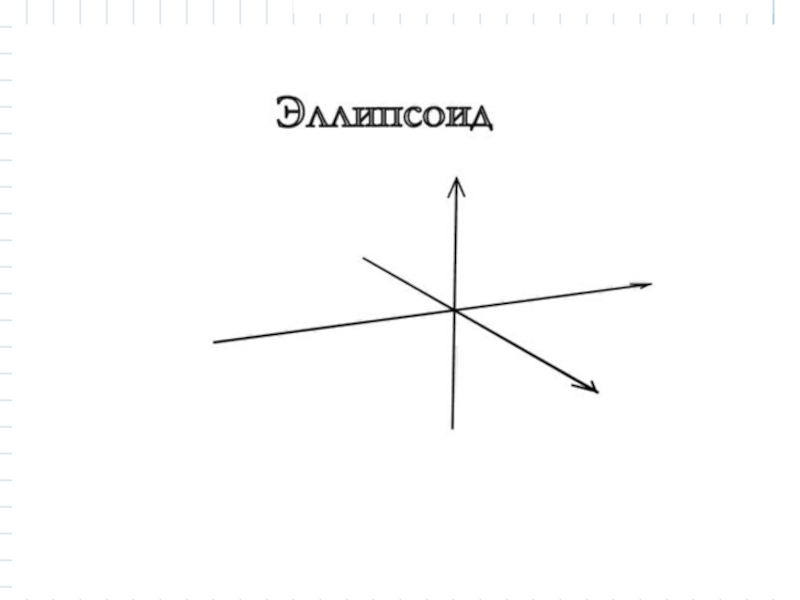
- 7. 2.1 Эллипсоид. Эллипсоидом называется поверхность второго порядка с каноническим уравнением:
- 8. или ИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙ.
- 9. или
- 11. Точно также рассматриваются сечения эллипсоида другими плоскостями: Выполненное исследование завершается построением чертежа:
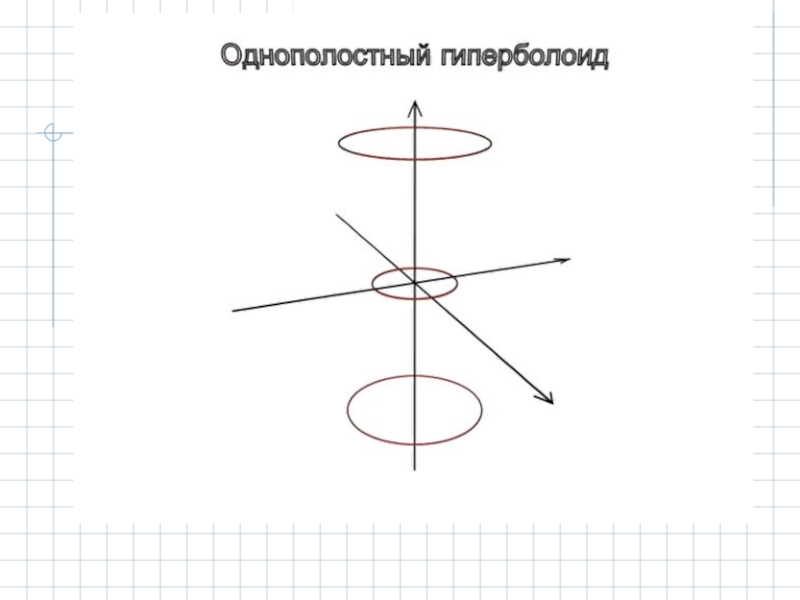
- 13. 2.2 Гиперболоиды. 2.2.1 Однополостный гиперболоид.
- 14. определяющей эллипс с полуосями а
- 15. В сечении плоскостью
- 16. задаёт гиперболу, пересекающую ось OY. Уравнение линии пересечения
- 18. 2.2.2 Двухполостный гиперболоид. Двухполостным гиперболоидом называется поверхность второго порядка с каноническим уравнением:
- 19. где Если
- 20. задает гиперболу, пересекающую ось OZ. Итоговый чертеж представлен на рисунке:
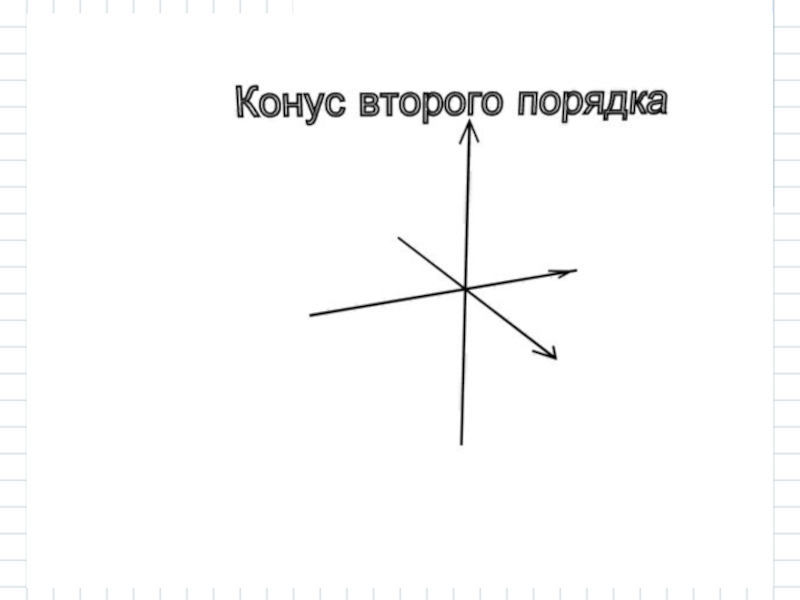
- 22. 2.3 Конус. Конусом второго порядка называется поверхность с каноническим уравнением
- 24. Замечание Осью конуса, заданного рассматриваемым каноническим уравнением,
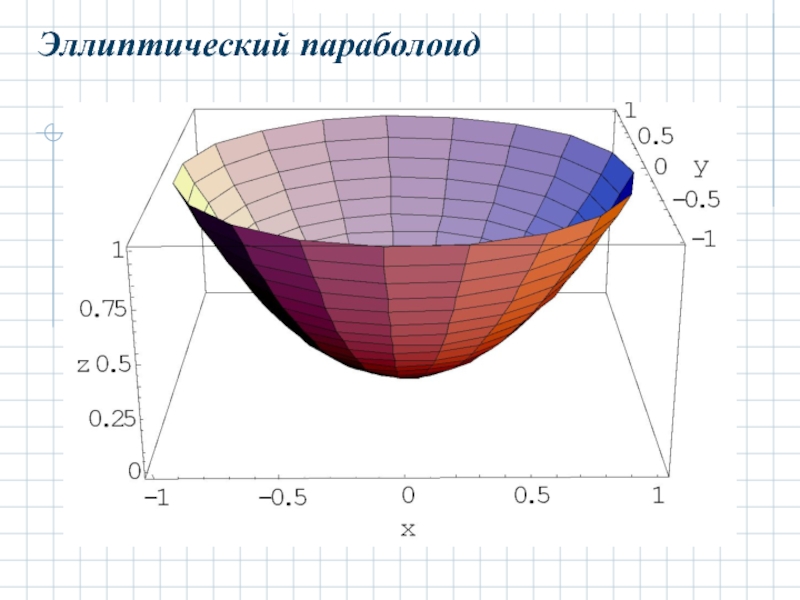
- 25. 2.4 Параболоиды. 2.4.1 Эллиптический параболоид.
- 26. Эллиптический параболоид
- 27. 2.4.2 Гиперболический параболоид. Гиперболическим параболоидом называется поверхность с каноническим уравнением:
- 28. Отсюда и название исследуемой поверхности, форма
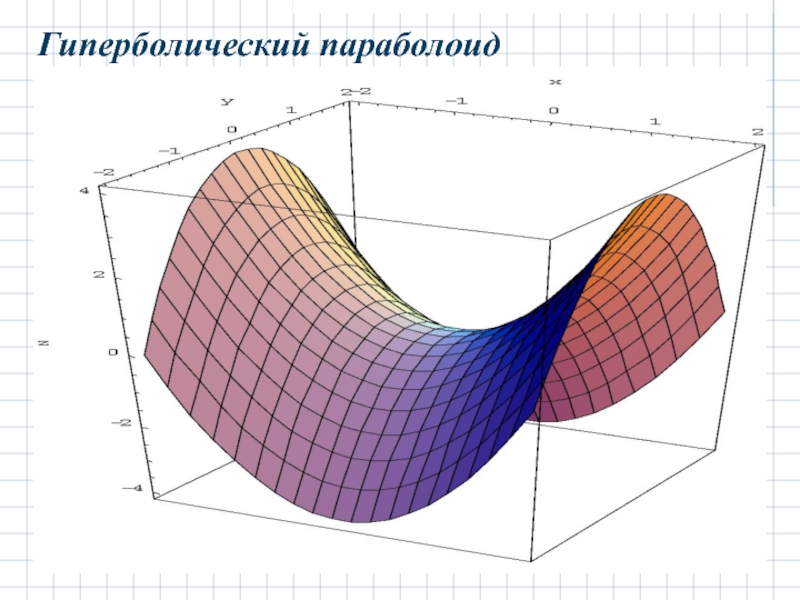
- 29. Гиперболический параболоид
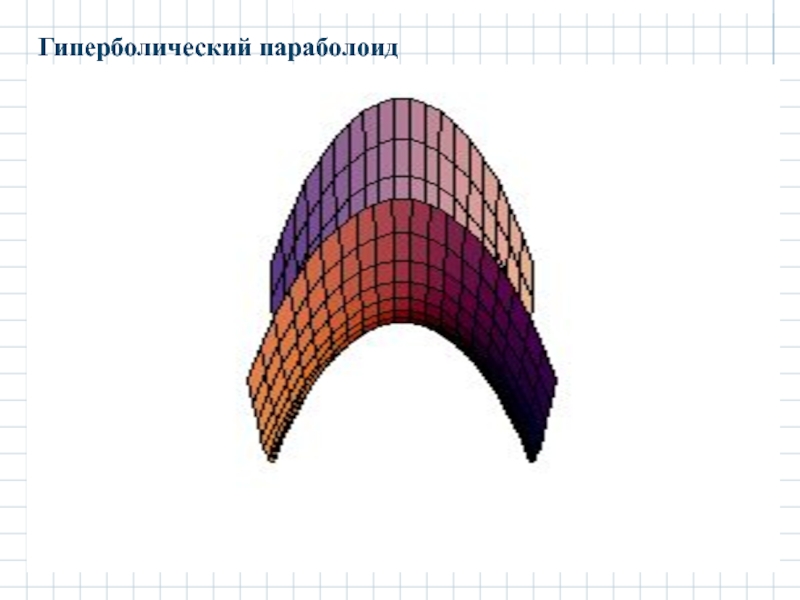
- 30. Гиперболический параболоид
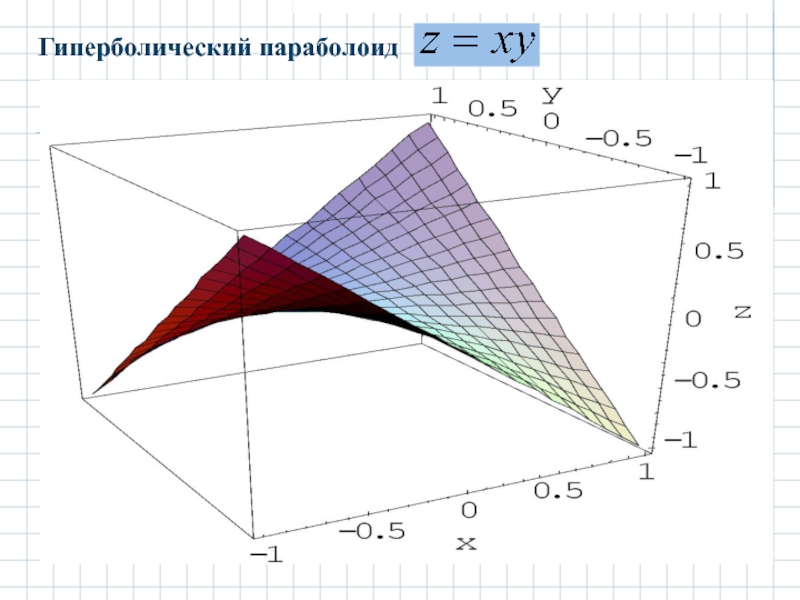
- 31. Гиперболический параболоид
- 32. 2.5 Цилиндры второго порядка .
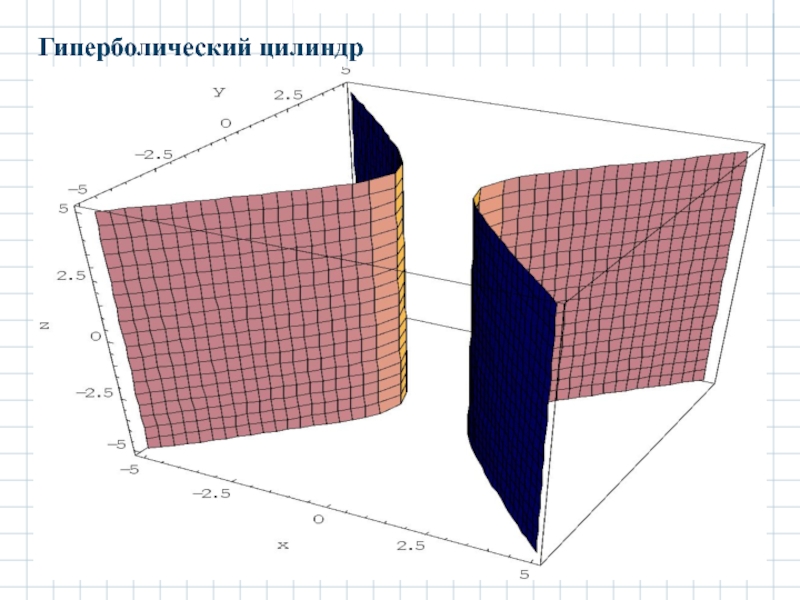
- 34. 2.5.2 Гиперболический цилиндр. Гиперболический цилиндр задается
- 35. Гиперболический цилиндр
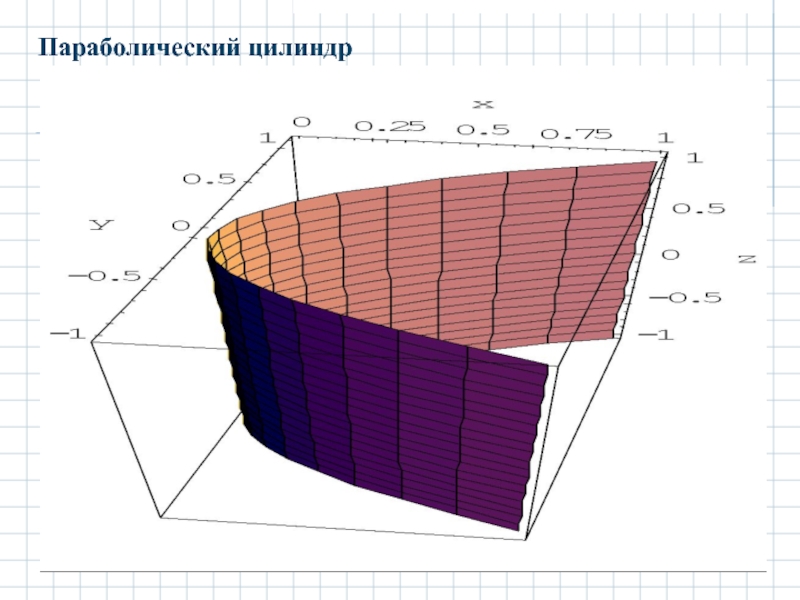
- 36. 2.5.2 Параболический цилиндр.
- 37. Параболический цилиндр
- 38. Замечание: Признаком рассмотренных цилиндрических поверхностей является отсутствие одной из переменных в каноническом уравнении.
Лекция 9 2. Исследование формы поверхностей второго порядка по их каноническим уравнениям. 1. Основные понятия. Поверхности второго порядка.
Слайд 2Лекция 9
2. Исследование формы поверхностей второго
порядка по их каноническим
уравнениям.
1. Основные понятия.
Поверхности второго порядка.
Слайд 3F(x,y,z) = 0,
(1)
которому удовлетворяют координаты каждой точки, принадлежащей поверхности, и не удовлетворяют координаты ни одной точки, не принадлежащей поверхности.
Уравнением поверхности называется уравнение с тремя переменными
Слайд 4Алгебраической поверхностью второго порядка называется поверхность , уравнение которой в декартовой
системе координат имеет вид
Ax2+By2+Cz2+2Dxy+2Exz+
2Fyz+Gx+Hy+Iz+K=0, (2)
где не все коэффициенты при слагаемых второго порядка (A,B,C,D,E,F) равны одновременно нулю.
Слайд 5Всякое уравнение (2), задающее невырожденную поверхность , путем преобразования координат
можно привести к каноническому виду ( при котором в уравнении поверхности отсутствуют слагаемые,содержащие смешанные произведения координат xy, xz, yz ).
Слайд 6Исследование формы поверхностей второго
порядка по их каноническим уравнениям.
Основным методом исследования формы
поверхности по её уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями, параллельными координатным плоскостям :
Слайд 7 2.1 Эллипсоид.
Эллипсоидом называется поверхность второго порядка с каноническим
уравнением:
Слайд 11Точно также рассматриваются сечения эллипсоида другими плоскостями:
Выполненное исследование завершается построением
чертежа:
Слайд 13 2.2 Гиперболоиды.
2.2.1 Однополостный гиперболоид.
Однополостным гиперболоидом называется поверхность второго порядка
с каноническим уравнением:
Слайд 14
определяющей эллипс с полуосями а и b.
ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА
МЕТОДОМ СЕЧЕНИЙ.
Слайд 18 2.2.2 Двухполостный гиперболоид.
Двухполостным гиперболоидом называется поверхность второго порядка с каноническим
уравнением:
Слайд 19
где
Если – с < h < c - нет
точек пересечения.
ИССЛЕДОВАНИЕ ФОРМЫ ДВУХПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.
Слайд 24Замечание
Осью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ.
Продольные сечения
являются прямыми линиями, поперечные сечения – эллипсы.
Слайд 25 2.4 Параболоиды.
2.4.1 Эллиптический параболоид.
Эллиптическим параболоидом называется поверхность с каноническим
уравнением:
Его форма показана на рисунке:
Слайд 27 2.4.2 Гиперболический параболоид.
Гиперболическим параболоидом называется поверхность с каноническим уравнением:
Слайд 28
Отсюда и название исследуемой поверхности, форма которой представлена на рисунке:
ИССЛЕДОВАНИЕ
ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.
Слайд 32 2.5 Цилиндры второго порядка .
2.5.1 Эллиптический
цилиндр.
Эллиптический цилиндр задается каноническим уравнением
Осью цилиндра является координатная ось OZ, поперечные сечения – эллипсы.
Слайд 34 2.5.2 Гиперболический цилиндр.
Гиперболический цилиндр задается каноническим уравнением:
Его форма представлена
на рисунке:
Слайд 36 2.5.2 Параболический цилиндр.
Параболический цилиндр задается каноническим уравнением:
Его
форма представлена на рисунке:
Слайд 38Замечание:
Признаком рассмотренных цилиндрических поверхностей является отсутствие одной из переменных в каноническом
уравнении.
