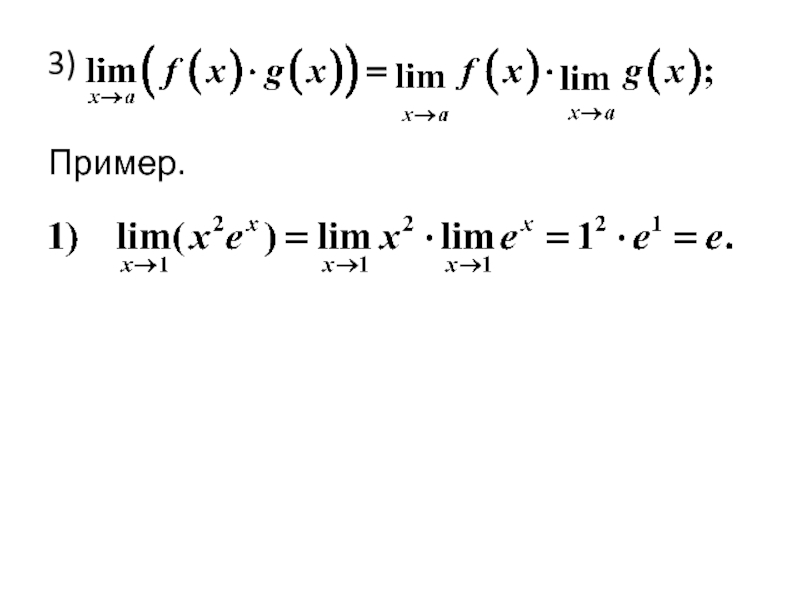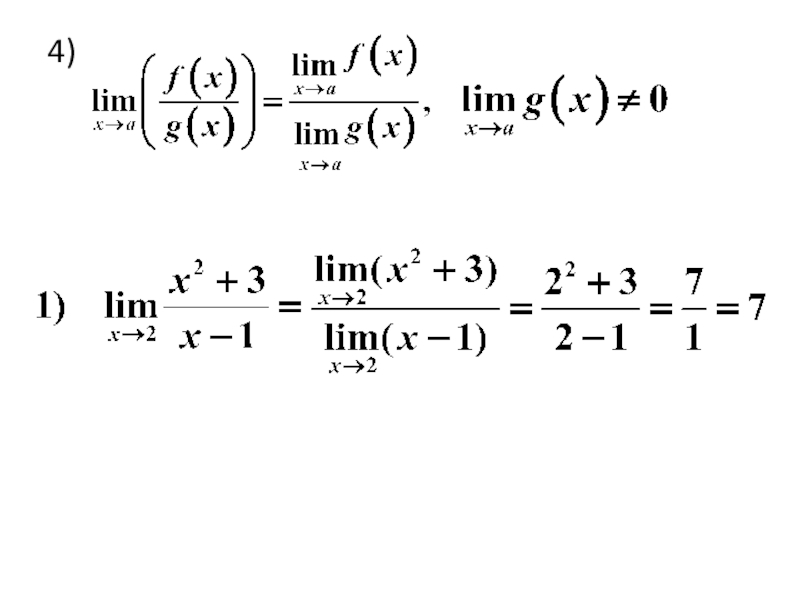- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
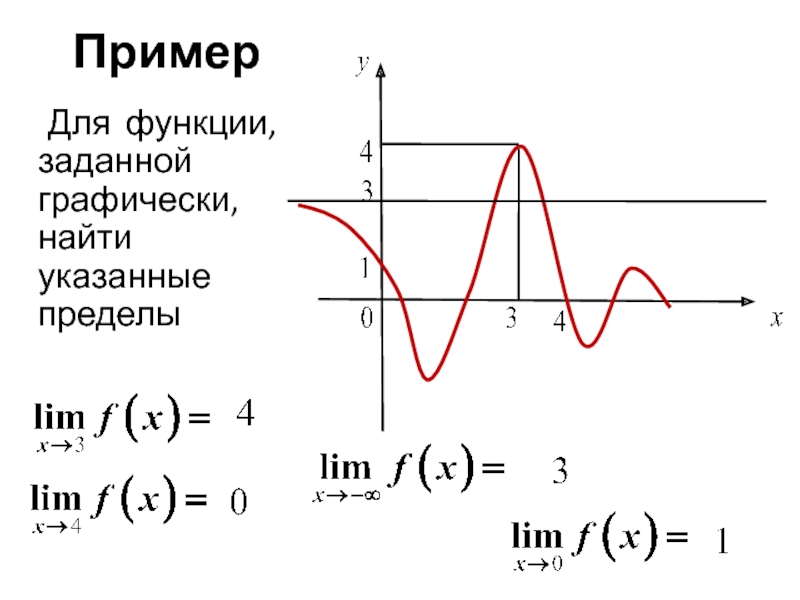
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
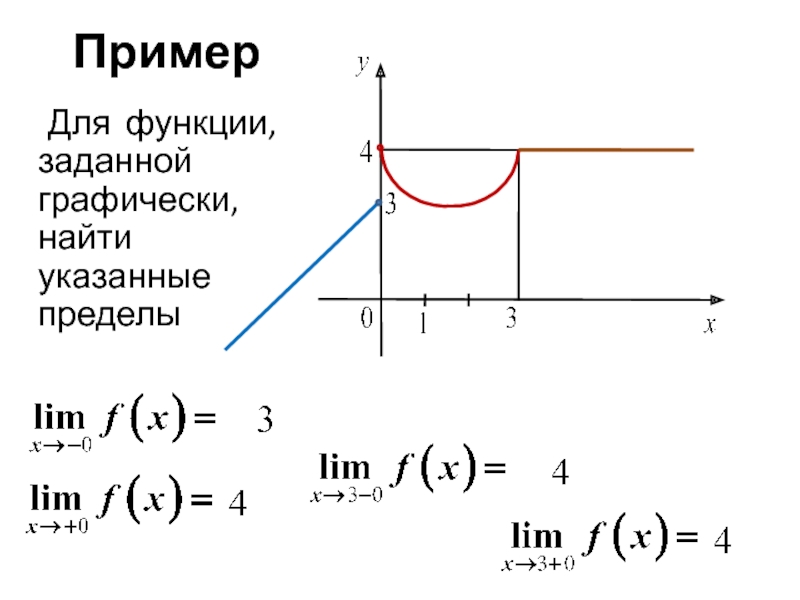
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в математический анализ презентация
Содержание
- 1. Введение в математический анализ
- 2. §1. МНОЖЕСТВА И ФУНКЦИИ ОПР. Под множеством
- 3. Основные числовые множества:
- 5. § 2. Функции, их свойства. График
- 6. Пусть задана функция Если элементами множеств
- 7. График функции ОПР. Графиком функции
- 8. Способы задания функций одной переменной Задать функцию
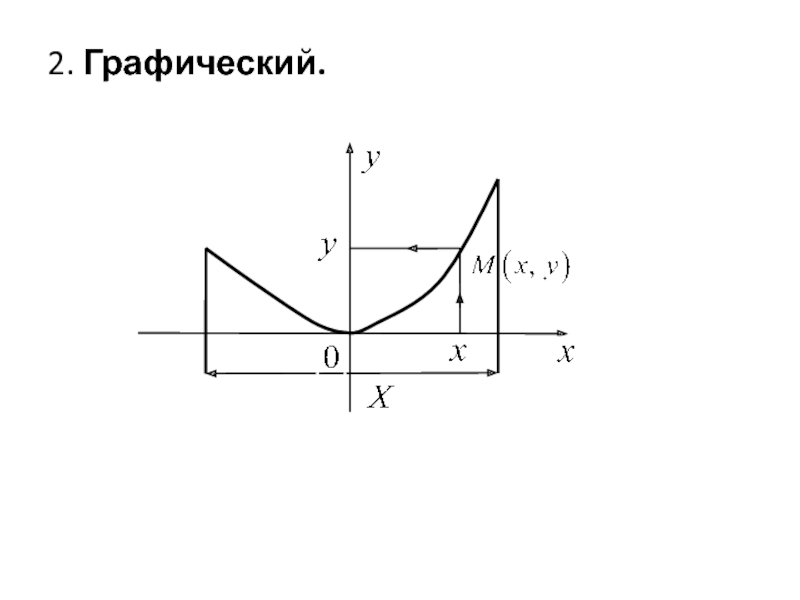
- 9. 2. Графический.
- 10. Аналитический. Например,
- 11. СЛОЖНАЯ ФУНКЦИЯ Пусть функция
- 12. Функция считается
- 13. Свойства функций одной переменной Четность и нечетность
- 14. §2. Предел функции
- 15. Окрестность точки Окрестностью
- 16. Если из окрестности
- 17. Число A называется пределом функции
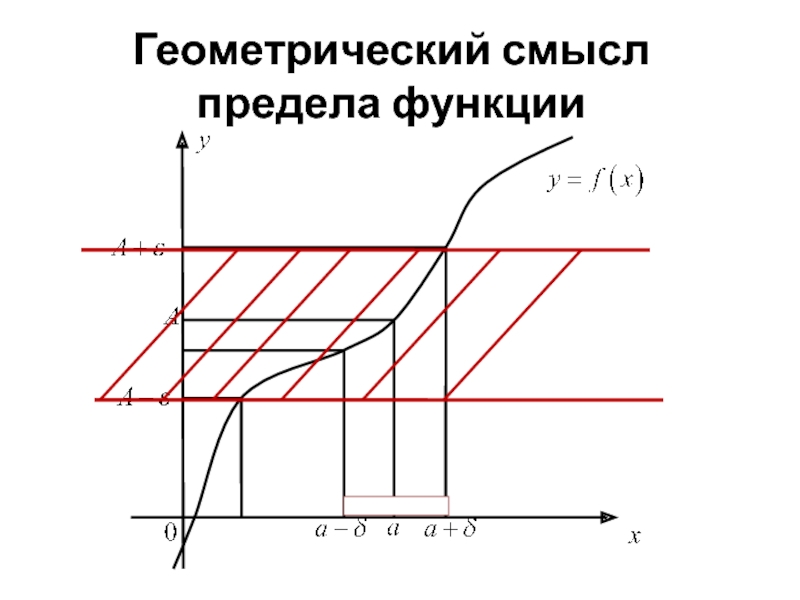
- 18. Геометрический смысл предела функции
- 19. это значит, что для любой
- 20. Пример Для функции, заданной графически, найти указанные пределы
- 21. 4.2. Односторонние пределы ОПР. Если значения функции
- 22. Если х принимает только значения большие
- 23. Значения односторонних пределов обычно записывают следующим образом:
- 24. Если существует , то
- 25. Пример Для функции, заданной графически, найти указанные пределы
- 26. 4.3. Основные теоремы о пределах Предположим, что
- 27. Поскольку для основных элементарных функций во всех
- 28. 1) Пример. Арифметические операции над пределами:
- 29. 2) Пример.
- 30. 3) Пример.
- 31. 4)
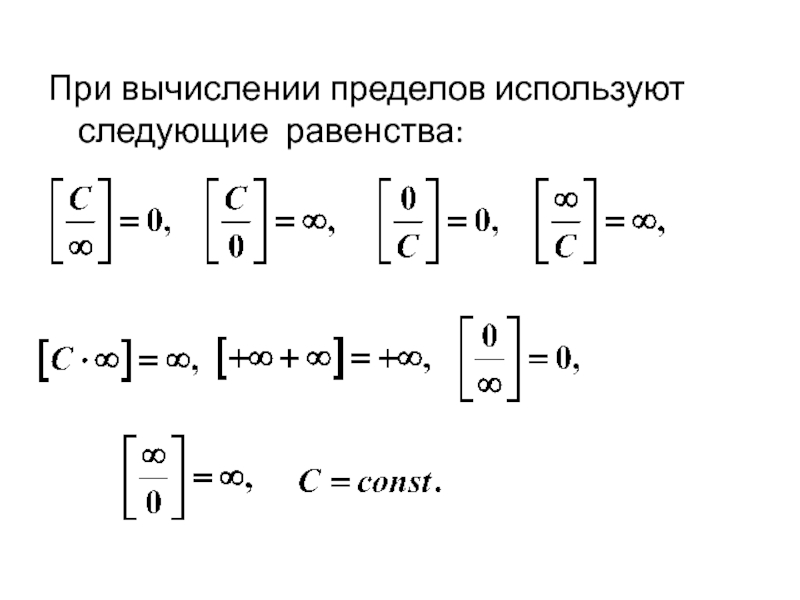
- 32. При вычислении пределов используют следующие равенства:
- 33. Пример Вычислить Решение.
- 34. 2. Вычислить Решение.
- 35. Однако, часто при подстановке в
- 36. Замечательные пределы При вычислении пределов выражений, содержащих
- 37. Справедливы также равенства
- 38. Равенства называются вторым замечательным пределом.
- 39. e является числом иррациональным, е= 2,718281828459045….
- 40. Логарифм по основанию е называется натуральным логарифмом
- 41. Раскрытие некоторых видов неопределенностей Неопределенность вида
- 42. Пример Решение. Найти предел функции
- 43. Б) При нахождении
- 44. Пример Вычислить Решение. При
- 45. В) При раскрытии неопределенности в случае иррациональных
- 46. Пример Вычислить Решение. При
- 47. В преобразованиях использовали формулу
- 48. 2.2. Неопределенность вида А). При
- 49. Пример Найти предел функции Решение. Имеем
§1. МНОЖЕСТВА И ФУНКЦИИ ОПР. Под множеством понимается совокупность объектов произвольной природы. Эти объекты называются элементами множества. Множества обозначаются обычно заглавными латинскими буквами: A, B, C и так далее, а их
Слайд 2§1. МНОЖЕСТВА И ФУНКЦИИ
ОПР. Под множеством понимается совокупность объектов произвольной природы.
Эти объекты называются элементами множества.
Множества обозначаются обычно заглавными латинскими буквами: A, B, C и так далее, а их элементы – строчными: a, b, c,...
Множества обозначаются обычно заглавными латинскими буквами: A, B, C и так далее, а их элементы – строчными: a, b, c,...
Слайд 3Основные числовые множества:
‑ множество натуральных чисел;
‑ множество целых чисел;
‑ множество рациональных чисел (множество конечных и периодических десятичных дробей);
‑ множество целых чисел;
‑ множество рациональных чисел (множество конечных и периодических десятичных дробей);
Слайд 4 ‑ множество действительных
(вещественных) чисел − это множество периодических и непериодических десятичных дробей ‑ числовая ось (прямая):
важнейшее свойство действительных чисел ‑ свойство непрерывности: действительные числа сплошь заполняют числовую ось, т.е. между двумя различными действительными числами всегда можно вставить новое действительное число.
важнейшее свойство действительных чисел ‑ свойство непрерывности: действительные числа сплошь заполняют числовую ось, т.е. между двумя различными действительными числами всегда можно вставить новое действительное число.
Слайд 5§ 2. Функции, их свойства.
График функции
Пусть даны два непустых множества
Соответствие , которое каждому элементу x множества X сопоставляет единственный элемент y множества Y, называется функцией и обозначается
или
Множество – область определения функции,
– множество значений.
Слайд 6 Пусть задана функция
Если элементами множеств Х и У являются действительные
числа, т. е. то функцию называют числовой функцией.
Переменная x называется при этом аргументом или независимой переменной,
а y – функцией или зависимой переменной.
Относительно величин x и y говорят, что они находятся в функциональной зависимости.
– частное значение функции при
Переменная x называется при этом аргументом или независимой переменной,
а y – функцией или зависимой переменной.
Относительно величин x и y говорят, что они находятся в функциональной зависимости.
– частное значение функции при
Слайд 7График функции
ОПР. Графиком функции
является множество
всех точек
плоскости ,
для каждой из которых значение аргумента x является абсциссой,
а значение функции y ‑ ординатой.
плоскости ,
для каждой из которых значение аргумента x является абсциссой,
а значение функции y ‑ ординатой.
Слайд 8Способы задания функций одной переменной
Задать функцию ‑ это значит указать множество
ее определения и правило, при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции.
Три основных способа задания функции:
1. Табличный.
Три основных способа задания функции:
1. Табличный.
Слайд 11СЛОЖНАЯ ФУНКЦИЯ
Пусть функция отображает числовое множество
в множество
, а функция отображает множество в множество .
Тогда функция
называется сложной функцией, или суперпозицией функций и .
Она определена на множестве и отображает его в множество .
, а функция отображает множество в множество .
Тогда функция
называется сложной функцией, или суперпозицией функций и .
Она определена на множестве и отображает его в множество .
Слайд 12 Функция считается промежу-точным аргументом для функции
.
Например, функцию можно рассматривать как сложную, образованную суперпозицией функций
и
Например, функцию можно рассматривать как сложную, образованную суперпозицией функций
и
Слайд 13Свойства функций одной переменной
Четность и нечетность функции.
2. Периодичность функции.
3. Монотонность
функции.
4. Ограниченность функции.
4. Ограниченность функции.
Слайд 15 Окрестность точки
Окрестностью точки
( ко-нечной точки) называется любой интервал, содержащий эту точку:
-окрестностью точки а называется интервал вида
-окрестностью точки а называется интервал вида
Слайд 17 Число A называется пределом функции
при , если для любого, как угодно малого , найдется такое число
, что для всех х, удовлетворяющих условию , будет выполнятся неравенство
C помощью логической символики:
, что для всех х, удовлетворяющих условию , будет выполнятся неравенство
C помощью логической символики:
Слайд 19
это значит, что для любой -окрестности точки A найдется такая
проколотая -окрестность точки ɑ , что для всех x из этой -окрестности соответствующие значения функции лежат в -окрестности точки A.
Т. Е. точки графика функции лежат внутри полосы шириной , ограниченной прямыми и
Т. Е. точки графика функции лежат внутри полосы шириной , ограниченной прямыми и
Слайд 214.2. Односторонние пределы
ОПР. Если значения функции
стремятся
к пределу при причем, х принимает только значения меньше , то записывают
и называют пределом слева в точке .
и называют пределом слева в точке .
Слайд 22 Если х принимает только значения большие чем
, то записывают
и называют пределом справа в точке
и называют пределом справа в точке
Слайд 23 Значения односторонних пределов обычно записывают следующим образом:
для предела слева
и
предела справа
Слайд 24 Если существует , то
существуют и оба односторонних
предела, причем
Справедливо и обратное утверждение: если существуют оба предела
и и они равны, то существует предел и
Если же , то не существует.
Справедливо и обратное утверждение: если существуют оба предела
и и они равны, то существует предел и
Если же , то не существует.
Слайд 264.3. Основные теоремы о пределах
Предположим, что существуют конечные пределы функций
и
при
Тогда имеют место следующие основные свойства конечных пределов.
при
Тогда имеют место следующие основные свойства конечных пределов.
Слайд 27 Поскольку для основных элементарных функций во всех точках их области определения
имеет место свойство
то при вычислении пределов, прежде всего вместо х подставляем предельное значение и, если значение определено, то используя арифметические операции над пределами, вычисляем предел.
то при вычислении пределов, прежде всего вместо х подставляем предельное значение и, если значение определено, то используя арифметические операции над пределами, вычисляем предел.
Слайд 35
Однако, часто при подстановке в
вместо x предельного значения
а получаются выражения вида:
и другие, которые называются неопределенностями и которые нужно «раскрывать» специальными методами.
и другие, которые называются неопределенностями и которые нужно «раскрывать» специальными методами.
Слайд 36Замечательные пределы
При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел
который
называется первым замечательным пределом.
Слайд 38Равенства
называются вторым замечательным пределом.
Здесь число е ‑ предел числовой последовательности
Слайд 39 e является числом иррациональным,
е= 2,718281828459045….
При практических вычислениях обычно ограничиваются
первыми двумя знаками после запятой.
Число е играет очень важную роль в математическом анализе.
Показательная функция с основанием е, называется экспонентой:
Число е играет очень важную роль в математическом анализе.
Показательная функция с основанием е, называется экспонентой:
Слайд 40 Логарифм по основанию е называется натуральным логарифмом и обозначается ln x.
Таким образом:
Слайд 41Раскрытие некоторых видов неопределенностей
Неопределенность вида
А) При вычислении предела дроби, содержащей
тригонометрические функции, в случае, когда предел и числителя, и знаменателя равен нулю, можно использовать первый замечательный предел.
Слайд 43Б) При нахождении отношения
двух
многочленов и , если
то следует числитель и знаменатель дроби разделить на разность один или несколько раз, пока не исчезнет неопределенность.
многочленов и , если
то следует числитель и знаменатель дроби разделить на разность один или несколько раз, пока не исчезнет неопределенность.
Слайд 44Пример
Вычислить
Решение. При числитель и знаменатель дроби стремятся
к нулю. Используем формулу
Слайд 45В) При раскрытии неопределенности в случае иррациональных выражений в числителе и
(или) знаменателе следует избавится от иррациональности путем умножения на соответствующее сопряженное выражение или производя замену переменных.
Слайд 46Пример
Вычислить
Решение. При числитель и знаменатель дроби равны нулю. Домножим
числитель и знаменатель на выражение, сопряженное числителю
, получим
, получим
Слайд 482.2. Неопределенность вида
А). При нахождении предела
отношения двух многочленов
и
при числитель и знаменатель дроби целесообразно разделить на , где n – высшая степень этих многочленов.
при числитель и знаменатель дроби целесообразно разделить на , где n – высшая степень этих многочленов.
Слайд 49Пример
Найти предел функции
Решение. Имеем неопределенность
Разделим числитель и знаменатель дроби на
тогда
