- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности вращения. Классификация поверхностей. (Лекция 3.3) презентация
Содержание
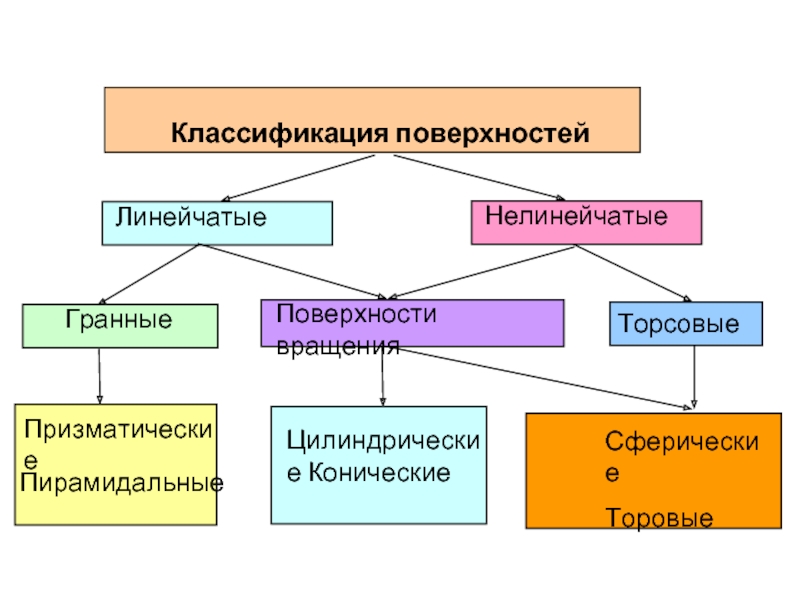
- 2. Классификация поверхностей
- 3. Образование поверхностей
- 4. Гранные поверхности 2.Призматические поверхности( Призма) 1.Плоскость: l
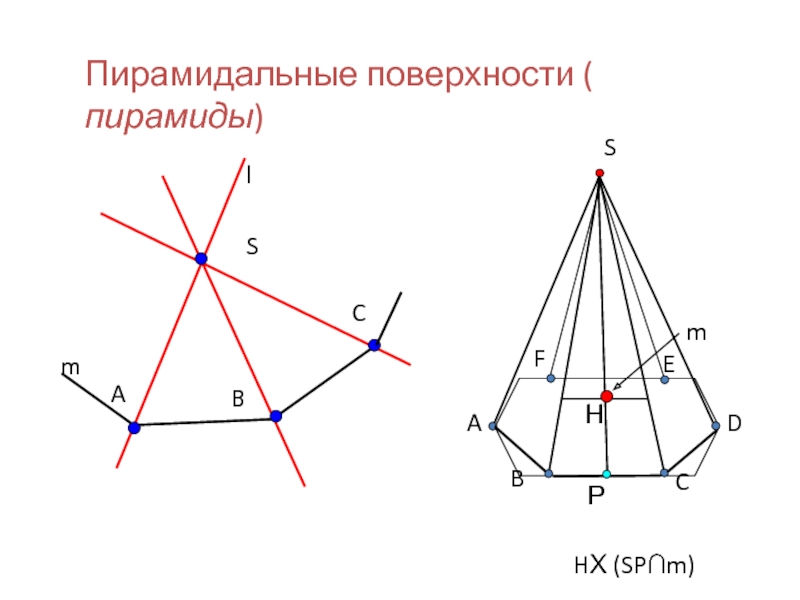
- 5. Пирамидальные поверхности ( пирамиды)
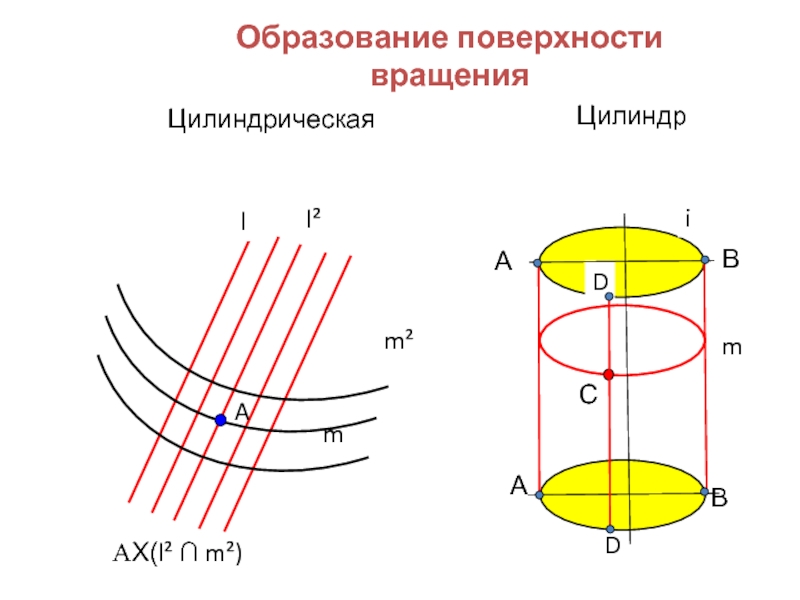
- 6. Образование поверхности вращения Цилиндрическая
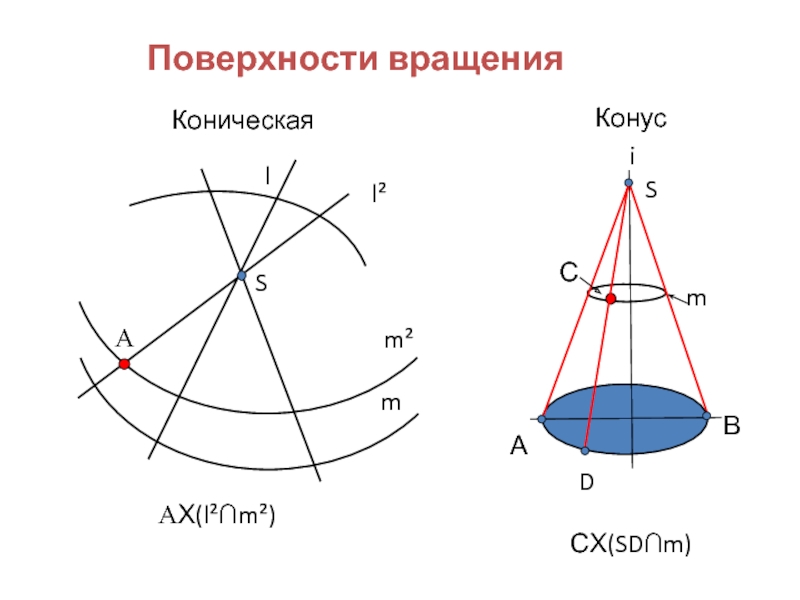
- 7. Поверхности вращения Коническая S l
- 8. Линейчатые поверхности с плоскостью параллелизма ·
- 9. Коноид – прямолинейная образующая движется по
- 10. Косая плоскостьКосая плоскость (гиперболический параболоид) – прямолинейная
- 11. Построить
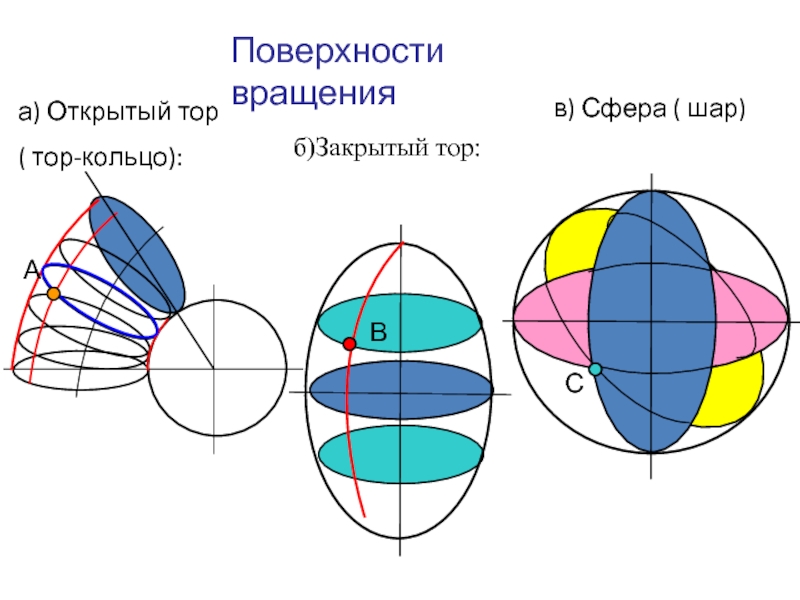
- 14. Поверхности вращения а)
- 15. Точки на гранных поверхностях А1 А2
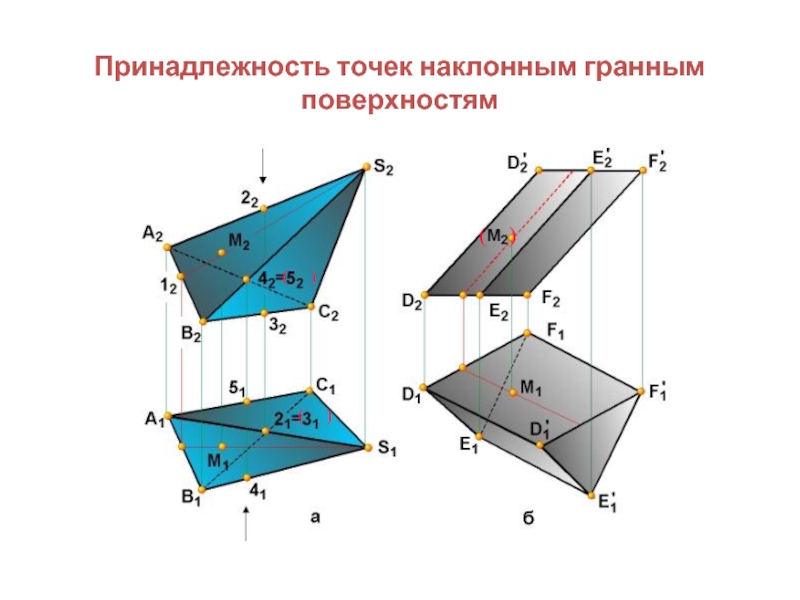
- 16. Принадлежность точек наклонным гранным поверхностям
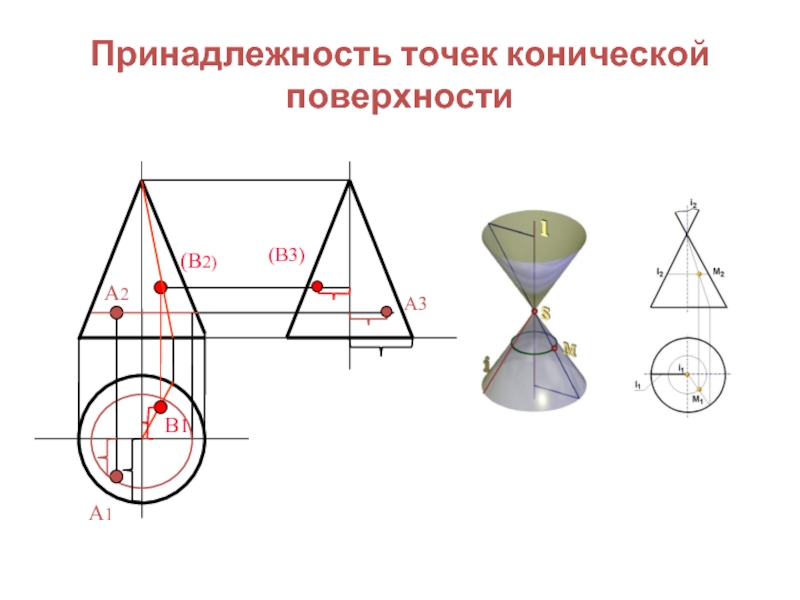
- 17. Принадлежность точек конической поверхности А2
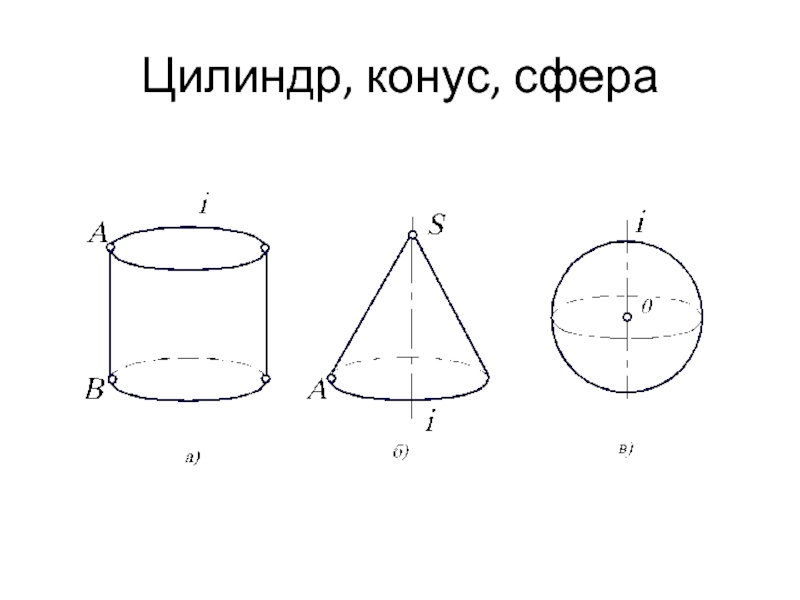
- 19. Цилиндр, конус, сфера
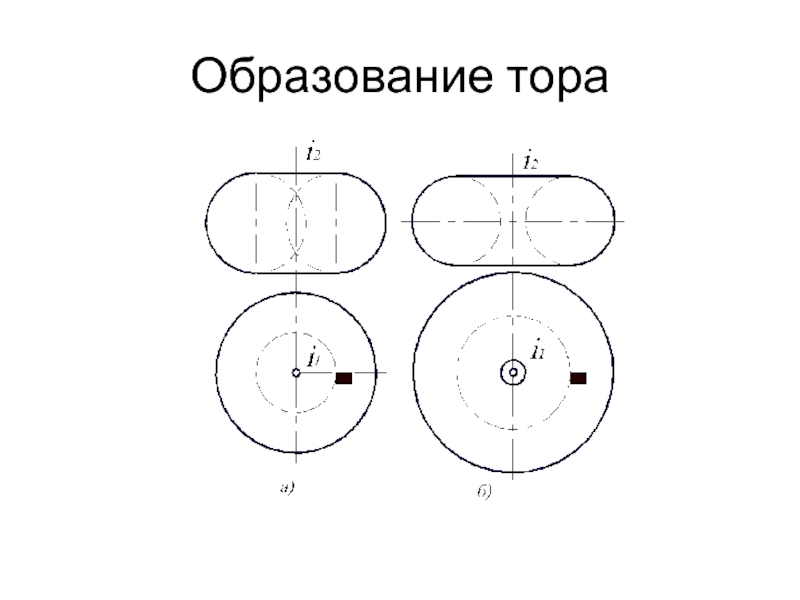
- 20. Образование тора
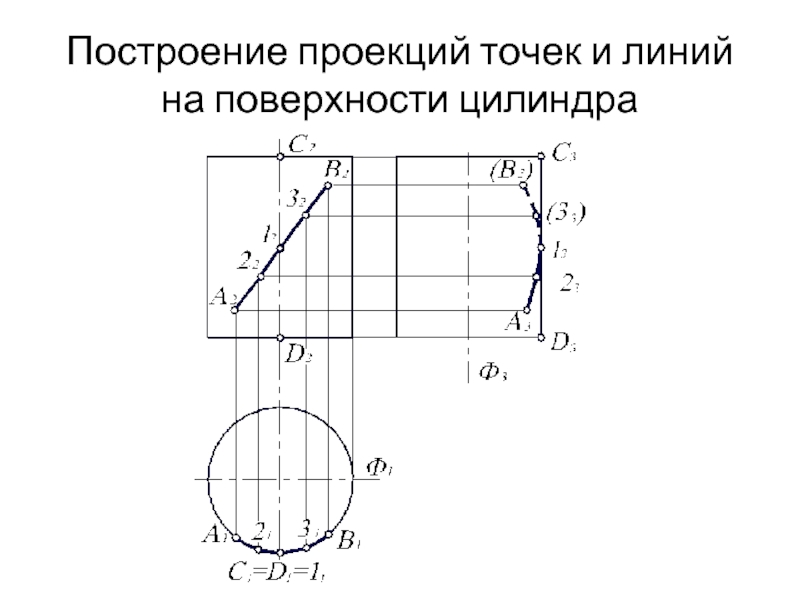
- 21. Построение проекций точек и линий на поверхности цилиндра
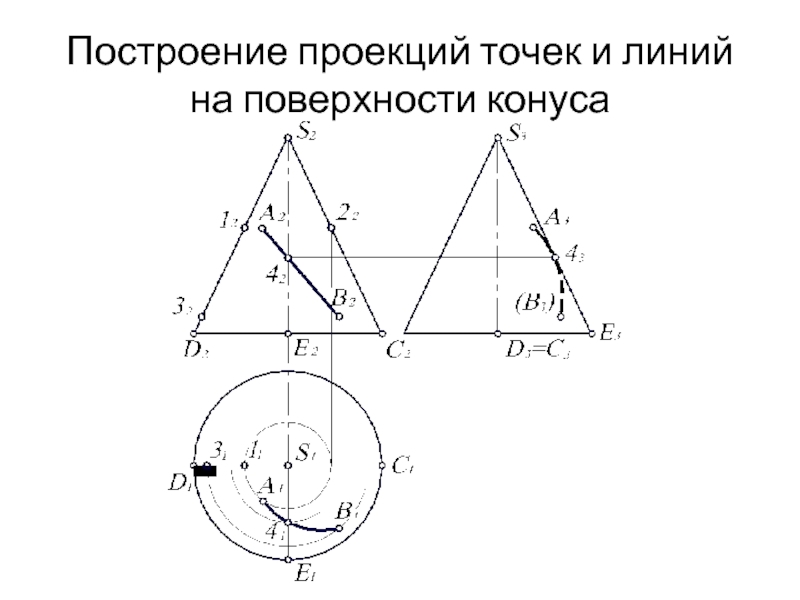
- 22. Построение проекций точек и линий на поверхности конуса
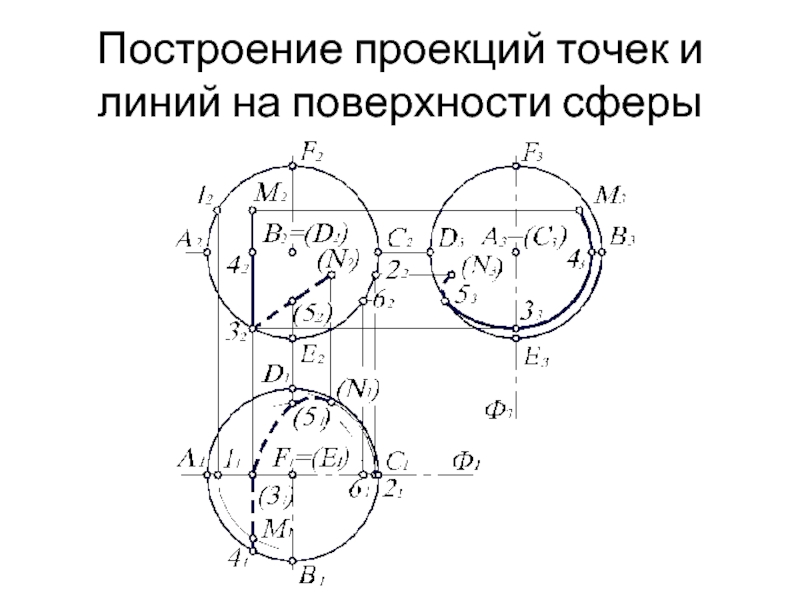
- 23. Построение проекций точек и линий на поверхности сферы
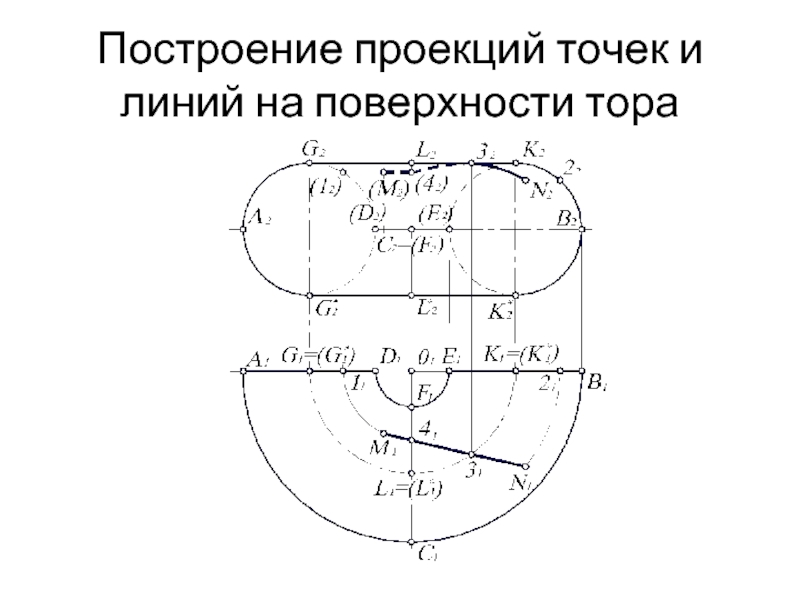
- 24. Построение проекций точек и линий на поверхности тора
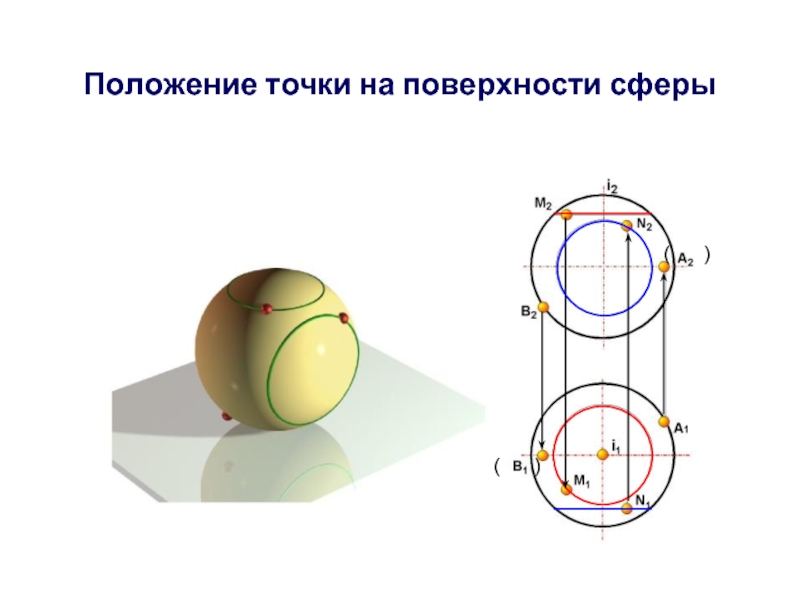
- 25. Положение точки на поверхности сферы ( ) ( )
- 26. Положение точек на поверхности сферы
- 27. Сечение сферы
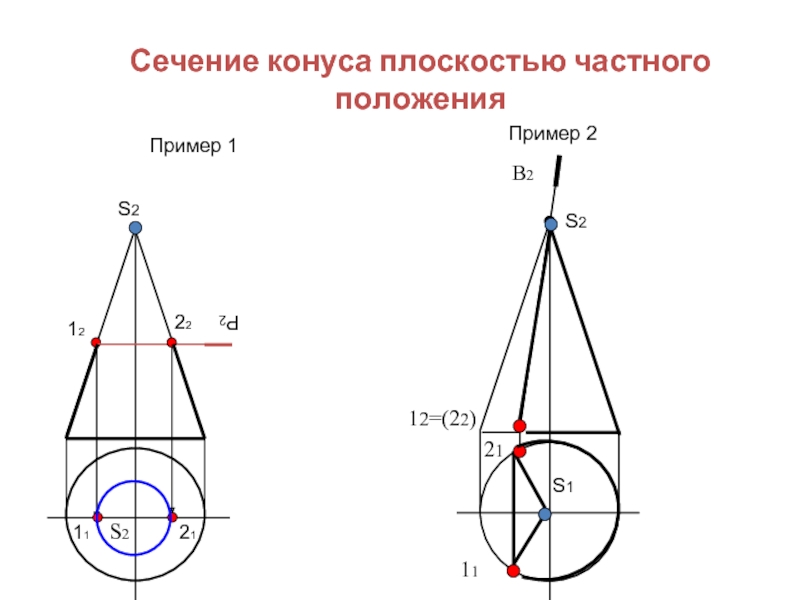
- 28. Сечение конуса плоскостью частного положения Пример 1
- 29. Пересечение поверхностей
- 30. 4.1.Сечение конуса плоскостью, параллельной одной образующей
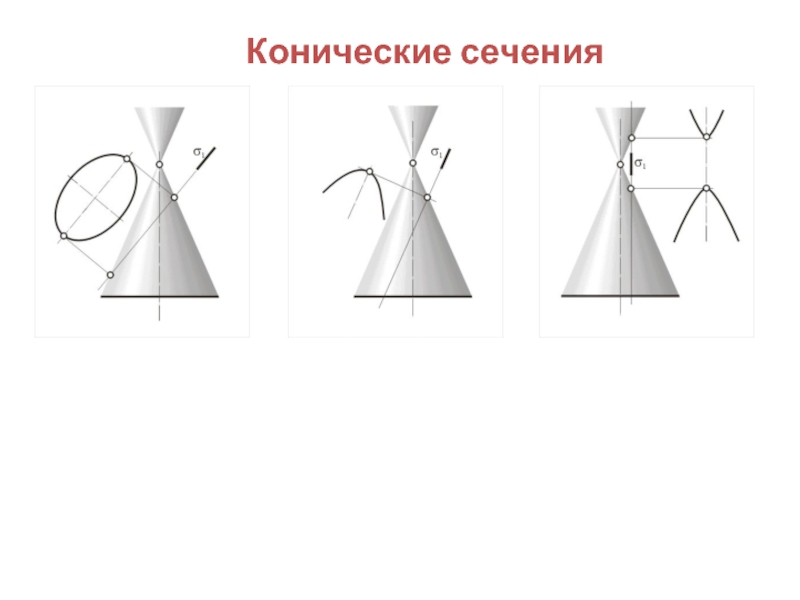
- 31. Конические сечения
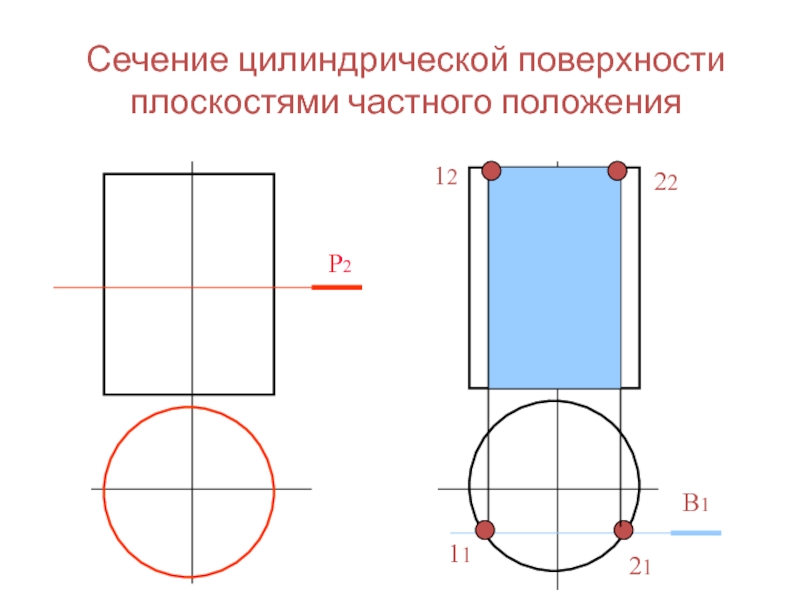
- 32. Сечение цилиндрической поверхности плоскостями частного положения
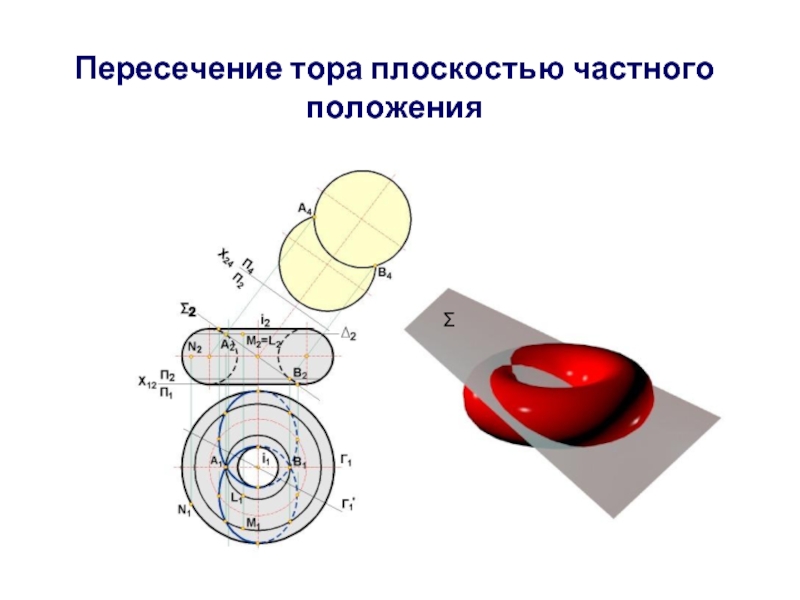
- 34. Пересечение тора плоскостью частного положения Σ
Слайд 3
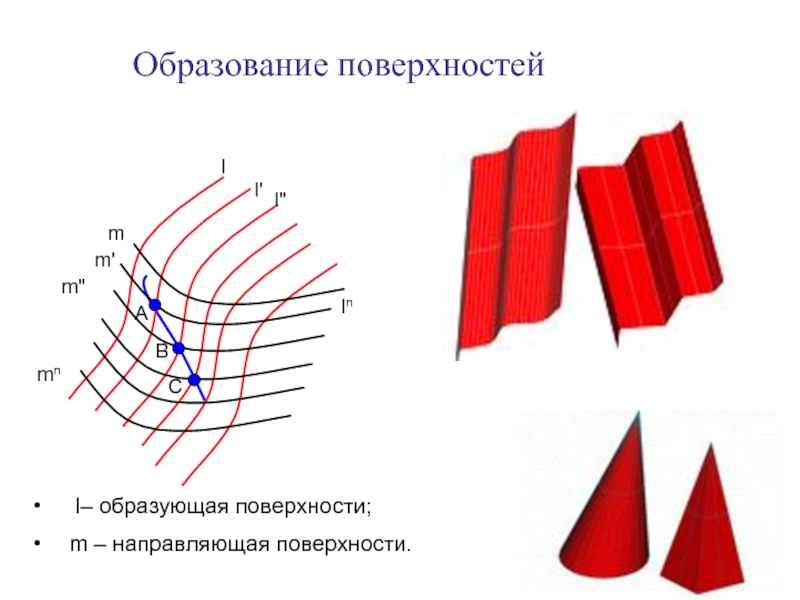
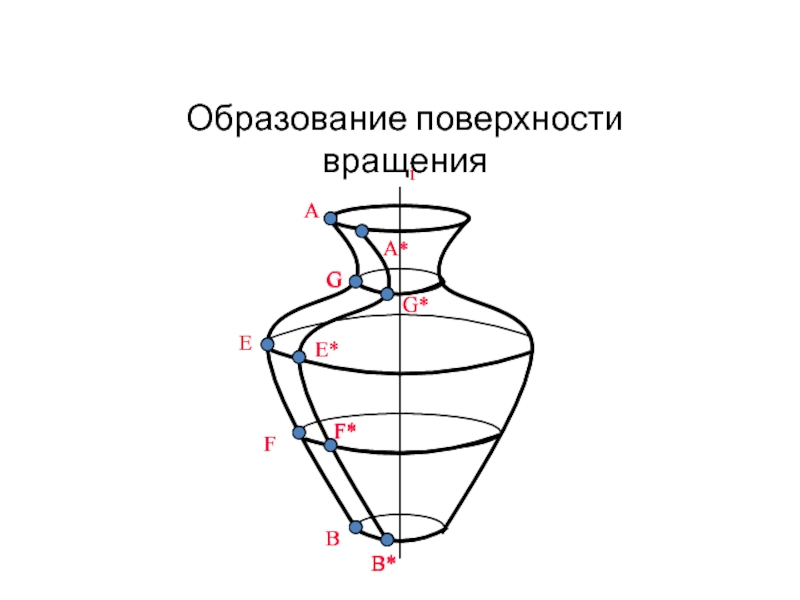
Образование поверхностей
l
l'
l"
ln
m
m'
m"
mn
A
C
B
l– образующая поверхности;
m – направляющая
поверхности.
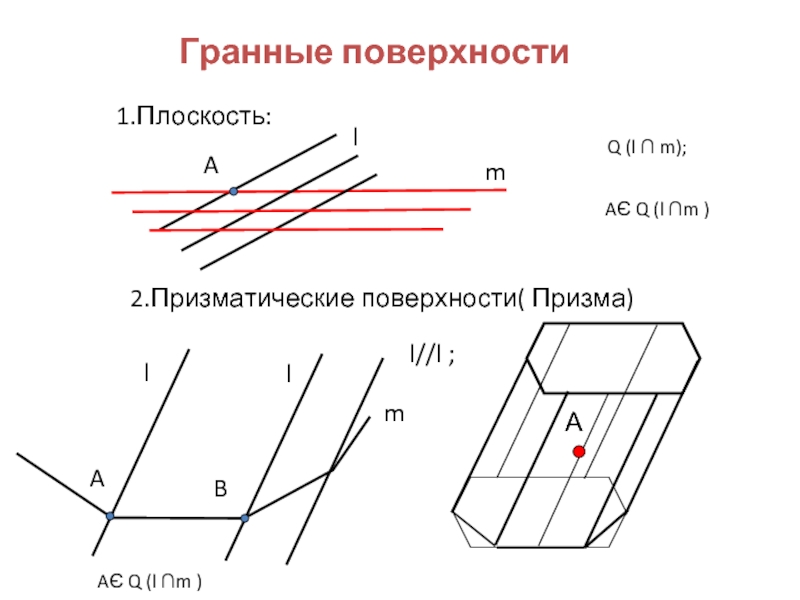
Слайд 4Гранные поверхности
2.Призматические поверхности( Призма)
1.Плоскость:
l
m
A
AЄ Q (l ∩m )
Q (l ∩ m);
l
m
l//l
;
l
A
AЄ Q (l ∩m )
B
А
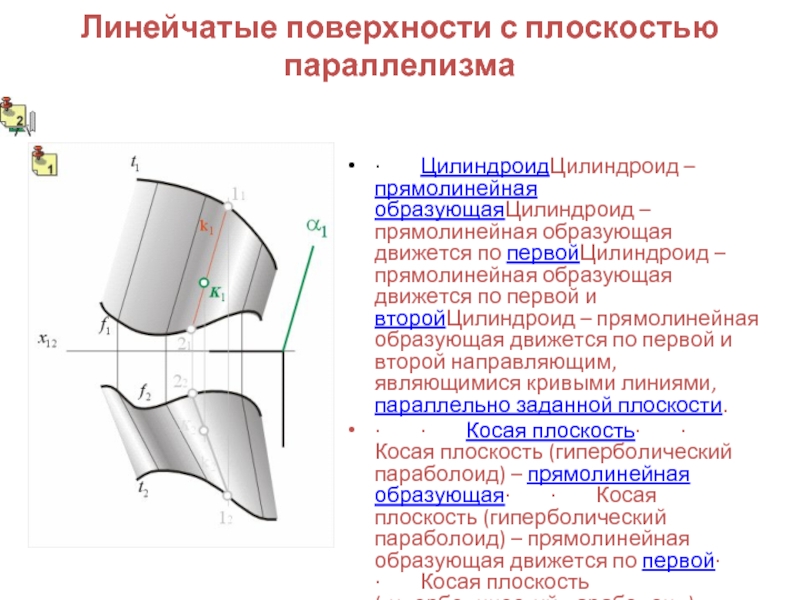
Слайд 8Линейчатые поверхности с плоскостью параллелизма
· ЦилиндроидЦилиндроид – прямолинейная образующаяЦилиндроид – прямолинейная
образующая движется по первойЦилиндроид – прямолинейная образующая движется по первой и второйЦилиндроид – прямолинейная образующая движется по первой и второй направляющим, являющимися кривыми линиями, параллельно заданной плоскости.
· · Косая плоскость· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй направляющим, являющимися прямыми линиями, параллельно заданной плоскости.
· · Косая плоскость· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй направляющим, являющимися прямыми линиями, параллельно заданной плоскости.
Слайд 9
Коноид – прямолинейная образующая движется по первой и второй направляющим, одна
из которых прямая линия, а вторая – кривая линия, параллельно заданной плоскости.
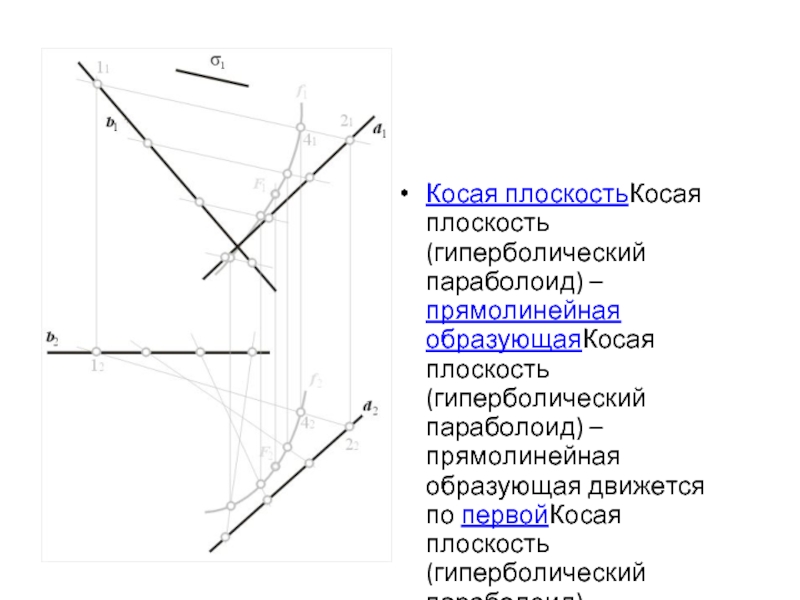
Слайд 10Косая плоскостьКосая плоскость (гиперболический параболоид) – прямолинейная образующаяКосая плоскость (гиперболический параболоид)
– прямолинейная образующая движется по первойКосая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второйКосая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй направляющим, являющимися прямыми линиями, параллельно заданной плоскости.
Слайд 11
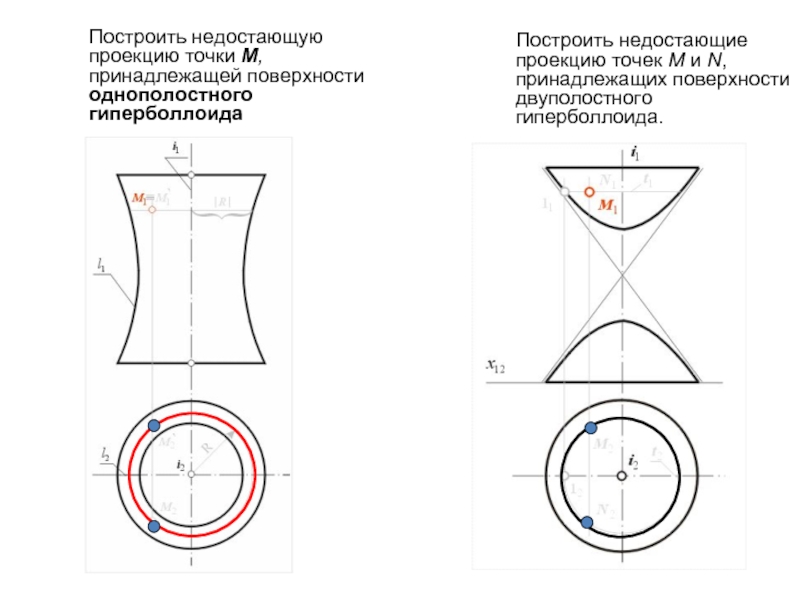
Построить недостающие проекцию точек М и N, принадлежащих поверхности двуполостного гиперболлоида.
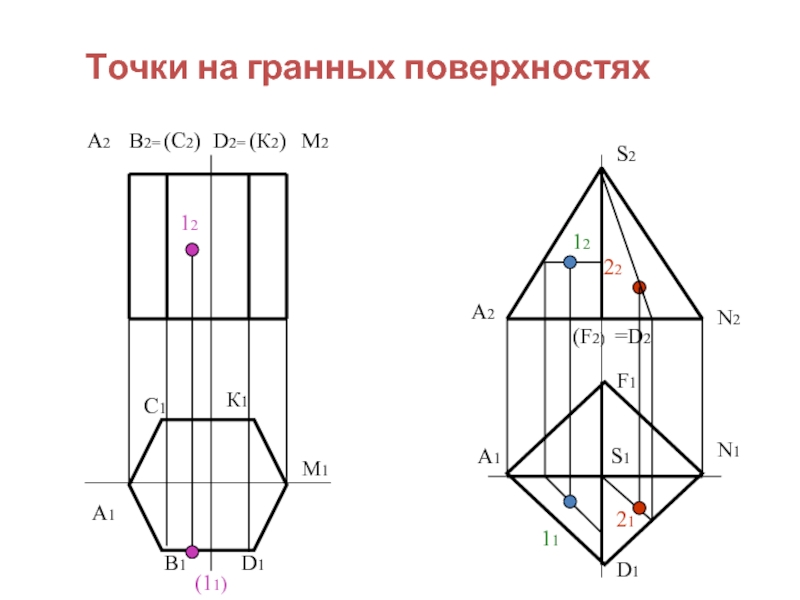
Слайд 15Точки на гранных поверхностях
А1
А2
В2=
В1
(С2)
С1
D2=
D1
(К2)
К1
М2
М1
12
(11)
S1
S2
A1
A2
(F2)
F1
=D2
D1
N2
N1
12
11
22
21
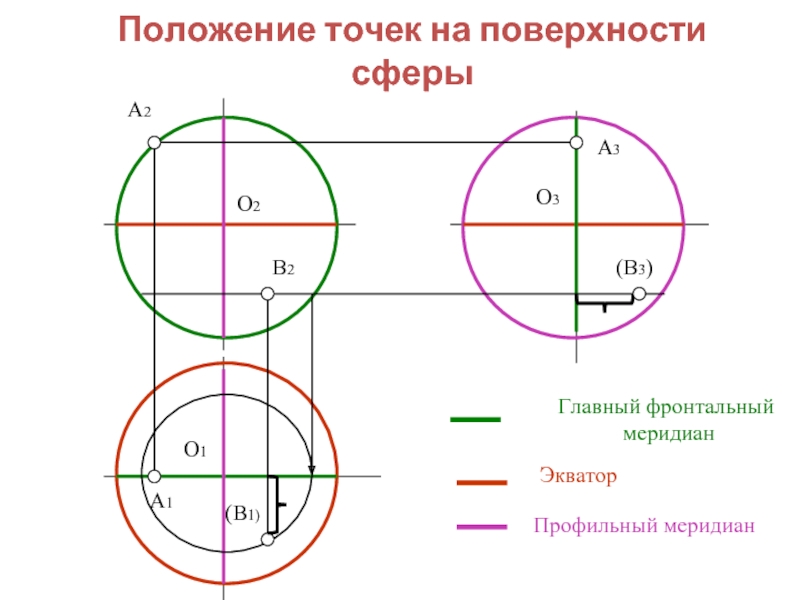
Слайд 26Положение точек на поверхности сферы
Главный фронтальный
меридиан
Профильный меридиан
Экватор
А2
А1
А3
В2
(В1)
(В3)
О2
О1
О3
Слайд 27
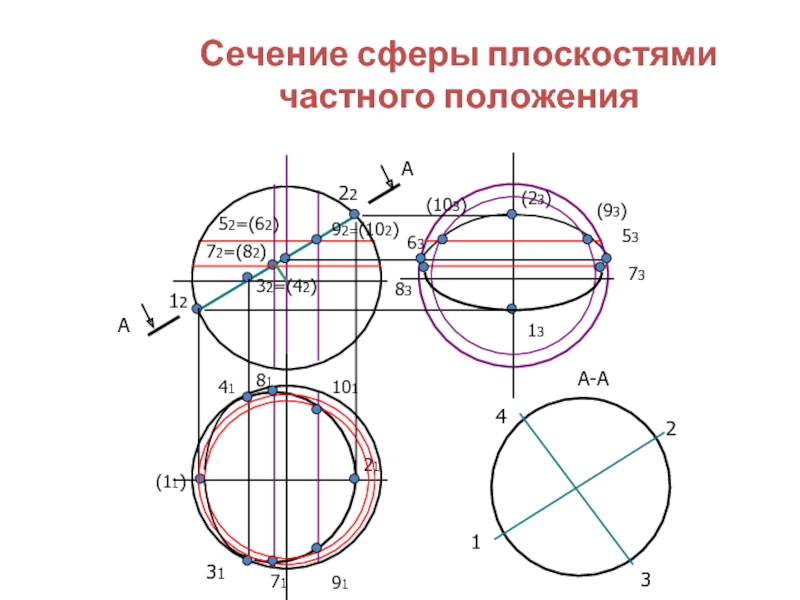
Сечение сферы плоскостями частного положения
А
А
12
22
52=(62)
31
41
(11)
21
13
(23)
53
63
92=(102)
72=(82)
32=(42)
71
81
91
101
(93)
(103)
73
83
А-А
1
2
3
4
Слайд 29
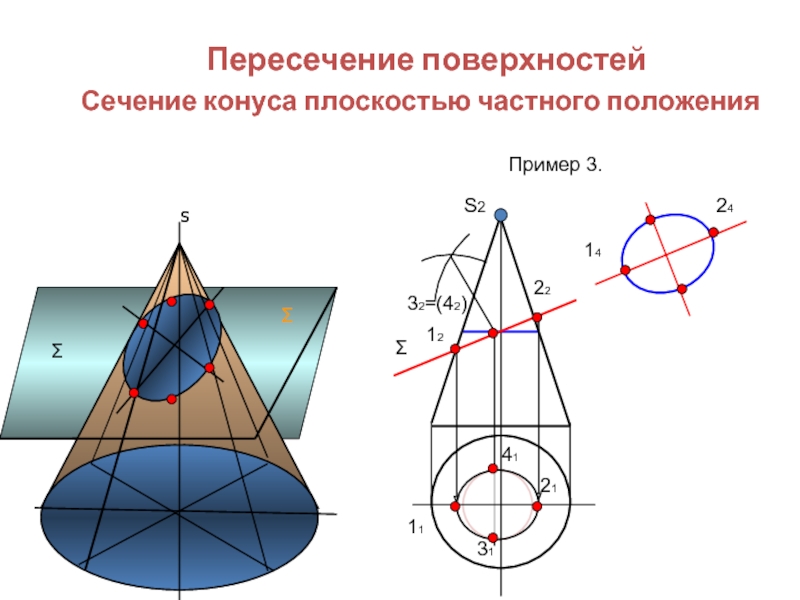
Пересечение поверхностей
Сечение конуса плоскостью частного положения
Пример 3.
S2
Σ
12
22
32=(42)
11
21
31
41
14
24
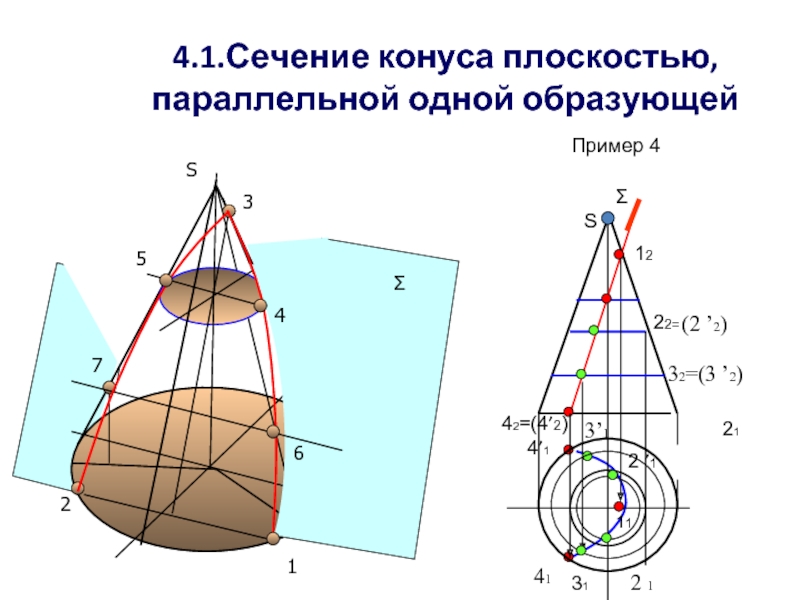
Слайд 304.1.Сечение конуса плоскостью, параллельной одной образующей
Пример 4
S
Σ
22=
2 ’1
42=(4’2)
11
21
31
4’1
12
2 1
41
3’1
(2 ’2)
32=(3 ’2)
Слайд 33
11
12
13
1
21
21’
23’
22 = (22’)
23
2’
2
31
31’
33’
33
51
52
53
5
32 =(32’)
3
3’
43
43’
41
42 =(42’)
41’
4
4’
Р
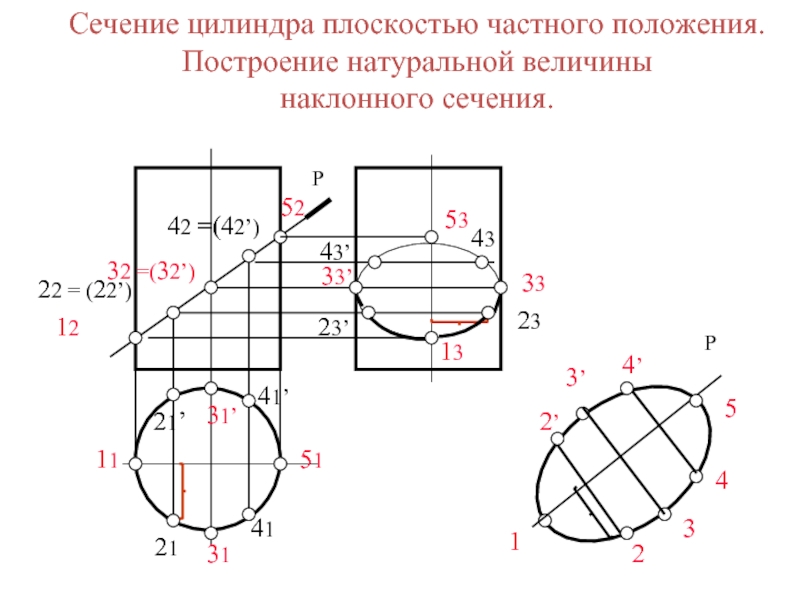
Сечение цилиндра плоскостью частного положения.
Построение натуральной
величины
наклонного сечения.
наклонного сечения.
Р