- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Небесная механика презентация
Содержание
- 1. Небесная механика
- 2. Законы Кеплера • Первый закон Кеплера…
- 3. Гравитационный потенциал Материальной точки • •
- 4. Притяжение пробной частицы внутри сферы: элементарные
- 5. Гравитационный потенциал шара Потенциал сферы
- 6. Гравитационный потенциал шара Теорема Дирихле
- 7. Гравитационный потенциал шара out inner
- 8. Гравитационный потенциал • • Интегрирование по
- 9. Гравитационный потенциал эллипсоида Теорема Лапласа Однородные
- 10. Задача Эйлера о двух неподвижных массах
- 11. Разложение потенциала в ряд Лапласа
- 12. Задача многих тел • Произвольная инерциальная
- 13. Задача двух тел: Произвольная инерциальная с.к.
- 14. Задача двух тел Относительная система координат
- 15. Задача двух тел. Интеграл Лапласа rI
- 16. Задача двух тел. Орбитальная с.к.
- 17. Задача двух тел
- 18. Уравнение Кеплера n (t )
- 19. Смещение перигелия Меркурия Ньютоновское приближение rg
- 20. Задача трех тел 2
- 21. Задача трех тел J
- 22. Кривые нулевой скорости m=0.04; x0=1.179;y0=0;z0=0.0; Vx0=0.0;Vy0=-0.238;Vz0=0.0; m=0.04; x0=1.12;y0=0;z0=0.0; Vx0=0.0;Vy0=-0.238;Vz0=0.0;
- 23. Точки Лагранжа L4,L5 x1/ 22 y
- 24. Семейство Хильды Резонанс 3:2 L3,L4,L5 – афелии астероидов
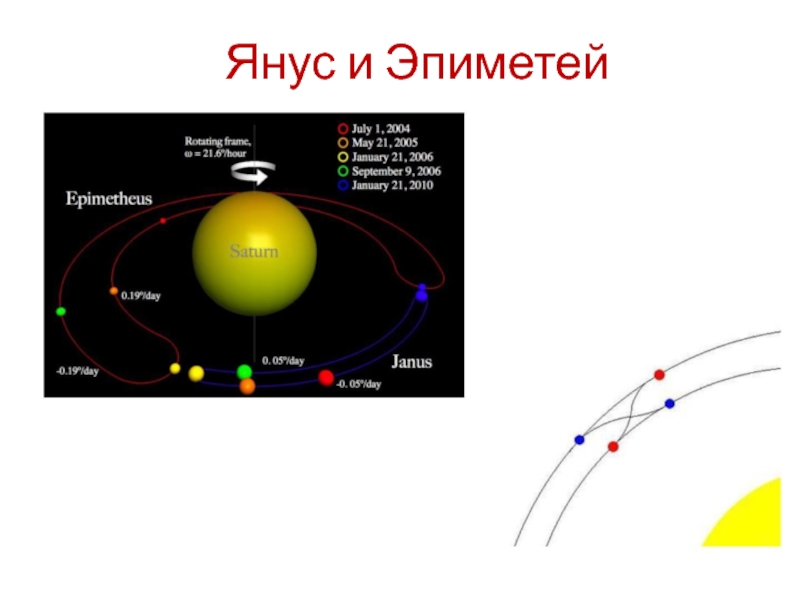
- 25. Янус и Эпиметей
- 26. Метод Лагранжа оскулирующих элементов
- 27. Метод Лагранжа оскулирующих элементов Разложение, усреднение
- 28. Метод Лагранжа или метод оскулирующих элементов
- 29. Метод Лагранжа или метод оскулирующих элементов
- 30. Метод Лагранжа или метод оскулирующих элементов
- 31. Метод Лагранжа или метод оскулирующих элементов
- 32. Спутник-пастух колец Сатурна Открытие в 1990г.
- 33. Спутник-пастухи Сатурна Прометей (внутренний) Пандора (внешний) Cassini image
- 34. Спутники-пастухи Cassini's confirmation that a small
- 35. Гиперион (спутник перевертыш) Двуликий… Япет Cassini images Спин-орбитальный резонанс
- 36. Астероид Круитни Орбитальный резонанс с Землей 1:1 Сопутствующая ситема к. Проекция на эклиптику
- 37. Сечение Пуанкаре Сечение (отображение) Пуанкаре –
- 38. Сечение Пуанкаре 1 2
- 39. Сечение Пуанкаре Потенциал Хенона-Хейлиса 1
- 40. Сечение Пуанкаре 1 2
- 41. Сечение Пуанкаре 1 2
- 42. Сечение Пуанкаре 1 2
- 43. Сечение Пуанкаре 1 2
Слайд 2
Законы Кеплера
•
Первый закон Кеплера… и длина эллипса
Параметрическое уравнение эллипса
x acos
y bsin
Длина
2
x
0
L dl rd
y d 4aE(e)
2 2
/2
E(e) d 1e
sin
2
-
полный эллиптический интеграл 2-го рода
2
0
Длина окружности
E(0) / 2
L 2a
Слайд 3
Гравитационный потенциал
Материальной точки
•
•
GM
r
Сферической оболочки
GM
r
GM
a
, ra
Sph
,
ra
Внутри сферической оболочки пробная частица находится в
Теорема Ньютона: обобщение на эллипсоидальный слой
Слайд 4
Притяжение пробной частицы внутри сферы:
элементарные соображения
Телесный угол
d dS r1
dS
2
2
1
2
2
2
F r dm r dS
2
dS r
1
1 2
2
F dm r
1
1
2
2
1
2
1
2
M S
F Const
2
r r
2
Слайд 5
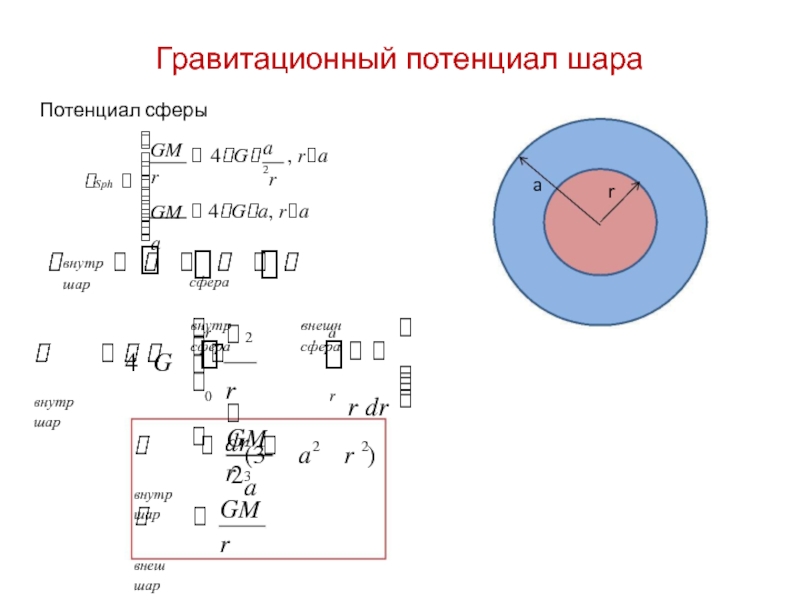
Гравитационный потенциал шара
Потенциал сферы
GM
r
GM
a
a
2
4G , ra
r
Sph
a
r
4Ga, ra
внутр внешн
сфера сфера
внутр
шар
сфера
r
dr
r
r
a
2
r dr
внутр
шар
4
G
0
r
GM
внутр
шар
(3
3
a
a r )
2
2
2
GM
r
внеш
шар
Слайд 6
Гравитационный потенциал шара
Теорема Дирихле
4G, внутри объема
вне объема
2
c
1
r
out
1
ra
out
c2
r
0
r
2
r r
r,out0, c 0, c GM
GM
r
out
2
2
out
G r2
1
2
c
1
r
ra
2
r 4 G
inner
c2
r
2
r r
3
Слайд 7
Гравитационный потенциал шара
out
inner ra
Учитываем сшивку на границе
потенциала и силы
ra
out
inner
ra
ra
Потенциал шара
GM
r
,
шар
GM
(3
a3
a r ), r a
2
2
2
Слайд 8
Гравитационный потенциал
•
•
Интегрирование по объему
Суммирование по элементарным
составляющим
•
Теорема Дирихле
Сфера, цилиндр, шар….
Слайд 9
Гравитационный потенциал эллипсоида
Теорема Лапласа
Однородные софокусные эллипсоиды притягивают внешнюю точку с силами,
одинаково
F M
x
/
/
F M
x
Теорема Ляпунова
Шар обладает минимальной потенциальной энергий
Слайд 10
Задача Эйлера о двух неподвижных массах
•
•
Гравитационный потенциал сжатого
сфероида эквивалентен потенциалу
стержня мнимой
Метод эквигравитирующих стержней
Слайд 12
Задача многих тел
•
Произвольная инерциальная с.к.
(0)
R R
R R
N
R G m
i
i
0
(0)
j
i
i
j
3
R R (t )
i
R
ij
j1
i
0
Порядок системы 6(n+1)
Первые интегралы:
m R a,
m R atb
закон движения центра масс
i i
i i
i
i
i i
Rm R I
закон сохранения момента количества движения
i
i
E TU
закон сохранения энергии
tot
В скалярном виде 10 первых интегралов в произвольной инерциальной с.к.
Слайд 13
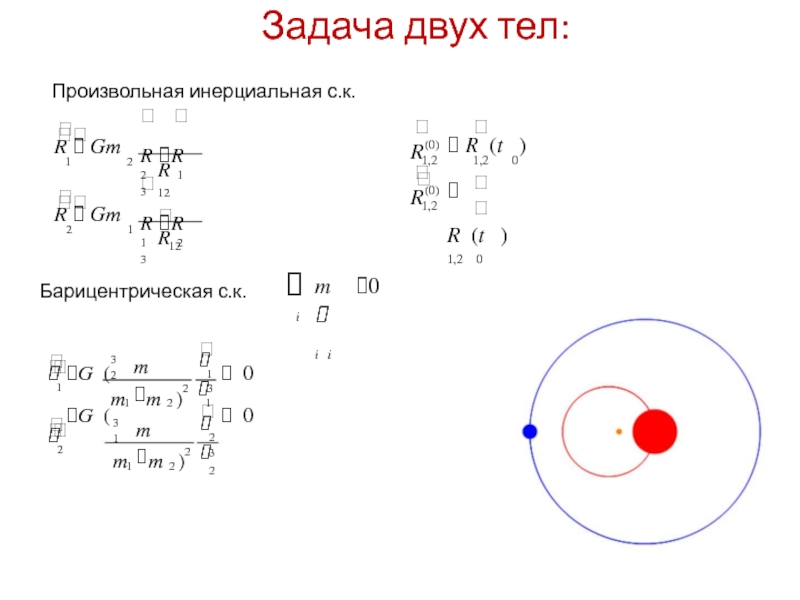
Задача двух тел:
Произвольная инерциальная с.к.
R R
2
3
R Gm
R
(0)
R (t )
1,2
1,2
0
1
2
R
12
R R
1 2
3
R (t )
1,2 0
R
(0)
1,2
R Gm
2
1
R
12
m
i i
0
Барицентрическая с.к.
i
m
3
2
m m )
1
G (
G (
0
0
1
2
3
1
2
1
m
3
1
m m )
2
3
2
2
2
1
2
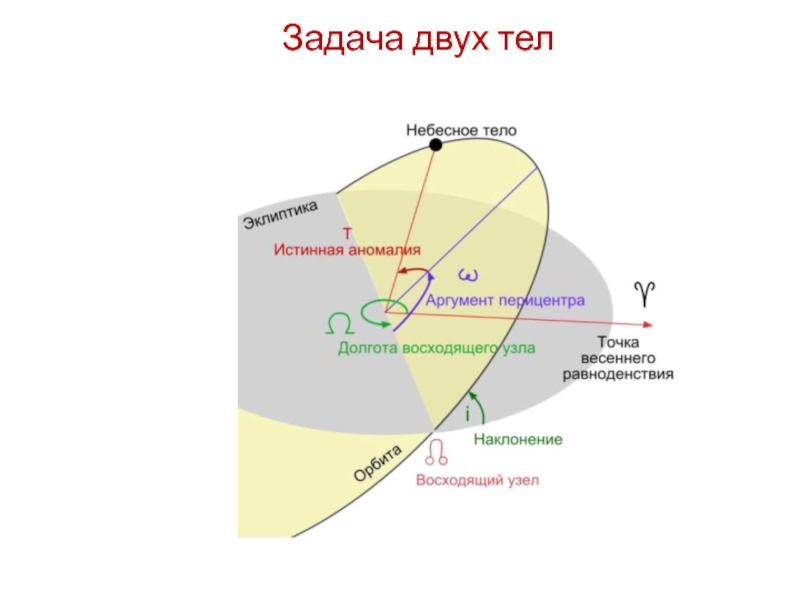
Слайд 14
Задача двух тел
Относительная система координат
r
rG(Mm) 0
r
3
r
(0)
(0)
r(t )
0
r
0
Первые интегралы:
rr I
момент на единицу массы
E TU
tot
Порядок системы =6, но 4 первых (в скалярах) интегралов. Не хватает…..
Слайд 15
Задача двух тел. Интеграл Лапласа
rI
r3
G(M m)
rI
0
Интеграл Лапласа
r
вектор
rI
r
Уравнения связи между первыми интегралами
I 0
5
независимых первых интегралов =>
Вектор момента и вектор Лапласа перпендикулярны
задача двух тел в относит с.к.
(система 6-го порядка) сводится к одному
уравнению
2
E I
tot
2
2
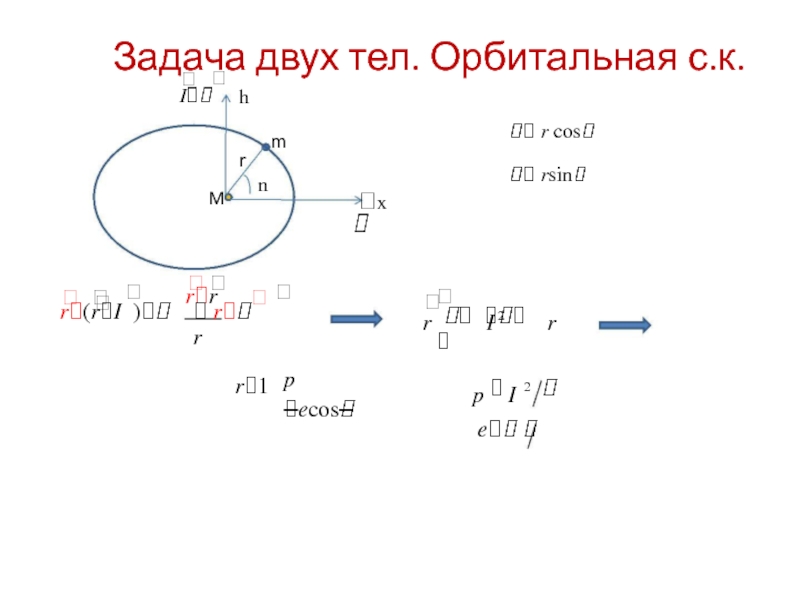
Слайд 16
Задача двух тел. Орбитальная с.к.
I
h
r cos
rsin
m
r
n
M
x
rr
r(rI )
r
I r
2
r
p
ecos
r1
p I
2
e
Слайд 18
Уравнение Кеплера
n
(t )
3/2
ecos ) p
dn
r2
n I
(1
n
2
0
n
tg
tg
1e 2
2
Уравнение Кеплера
a3/2
E esinE n(t )
T 2
G(M m)
Слайд 19
Смещение перигелия Меркурия
Ньютоновское приближение
rg 2
GM
2
du
dn
2GMm
2
Em
u
u
2
c
2
I
2
I
2
Релятивистская задача
2
rgmc2
du
d
n
m c
2 2
(1
E2
)
r u
g
3
u
2
u
I
2
I
2
m c
2 4
Максимальное смещение перигелия наблюдается для Меркурия и составляет
43’’ за 100 лет.
Слайд 20
Задача трех тел
2
r
2 r
r
1
1
3
3
r
r
1
2
U
x2ny
1,2
Gm1,2
x
U
y2nx
y
n
2
U(x, y,z)
2 (x2
y
)
U
2
1
r
1
2
z
z
2
2
V 2U C
J
C - интеграл Якоби (интеграл относительной энергии)
J
Слайд 21
Задача трех тел
J
n
2
2
V 2U C
U(x, y,z)
y
)
2
2
1
2
2
r r
1
2
Поверхности нулевой скорости
2
2
CJ
2
2
2
n (x y )
1
2
r r
1
2
CJ - интеграл Якоби
Слайд 22
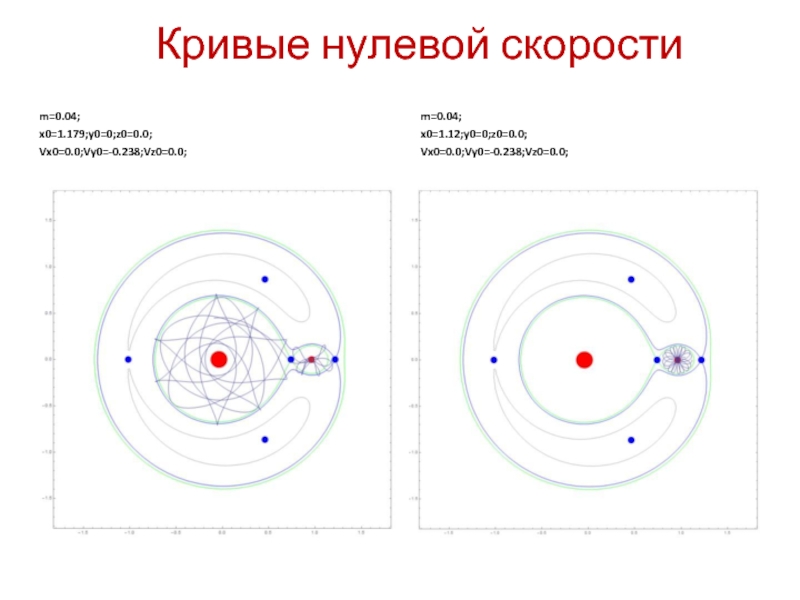
Кривые нулевой скорости
m=0.04;
x0=1.179;y0=0;z0=0.0;
Vx0=0.0;Vy0=-0.238;Vz0=0.0;
m=0.04;
x0=1.12;y0=0;z0=0.0;
Vx0=0.0;Vy0=-0.238;Vz0=0.0;
Слайд 23
Точки Лагранжа
L4,L5
x1/ 22
y 3 / 2
r r 1
1
2
2
1
L1,L2
1/3
2
31
r
2
L3
2
7
12 1
r 1
1
Слайд 26
Метод Лагранжа оскулирующих элементов
r
3
r
r F
возм
F
возм
0
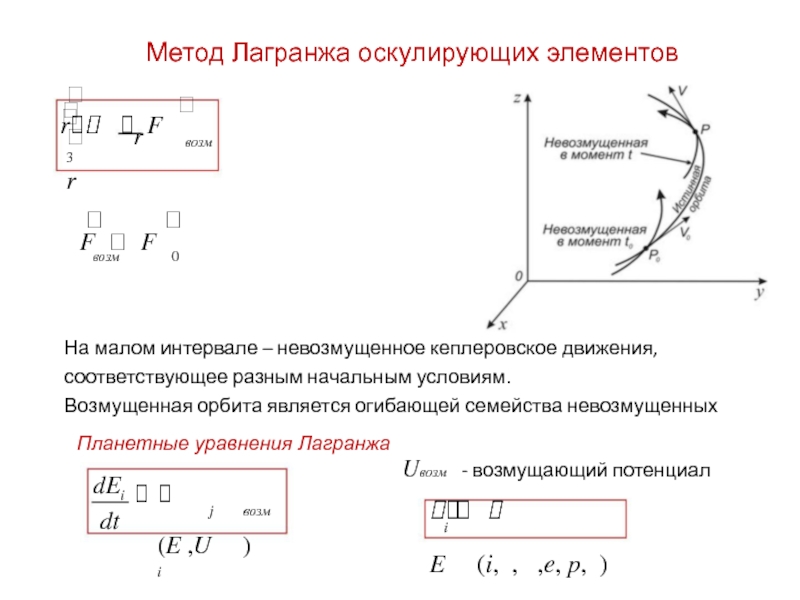
На малом интервале – невозмущенное кеплеровское движения,
соответствующее разным начальным условиям.
Возмущенная орбита является огибающей семейства невозмущенных
Планетные уравнения Лагранжа
Uвозм - возмущающий потенциал
dE
(E ,U )
i
i
E (i, , ,e, p, )
j
возм
dt
i
Слайд 27
Метод Лагранжа оскулирующих элементов
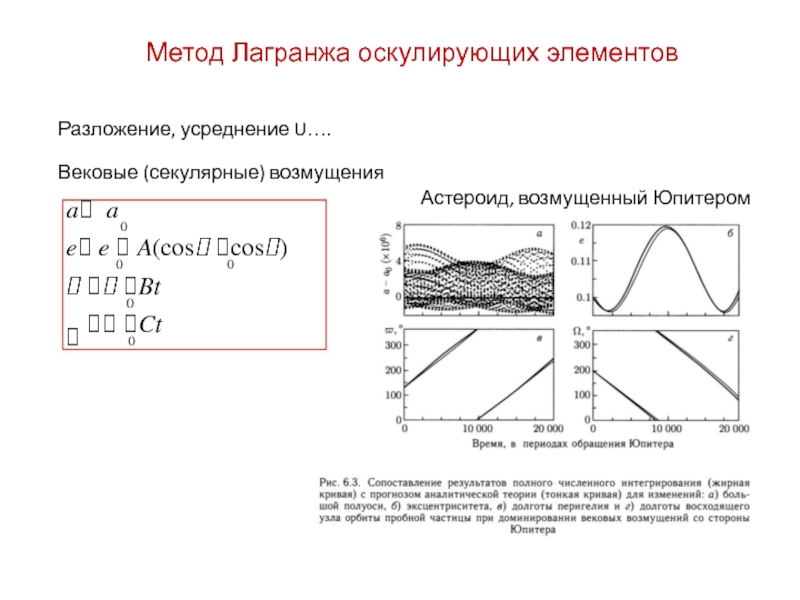
Разложение, усреднение U….
Вековые (секулярные) возмущения
Астероид, возмущенный Юпитером
a a
0
e
0
0
Bt
0
Ct
0
Слайд 28
Метод Лагранжа или
метод оскулирующих элементов
dE
(t,E j)
i
i
dt
Для двух планет
A
B
sin(k M k M )
cos(k M k M )
1 1 2 2
k ,k
k ,k
E E A (t t )
1
2
1
2
k n k n
0
0
0
1
1
2
2
k n k n
k1,k2
1 1
2 2
1 1
2 2
k1,2 – собственная частота движения
планеты и частота возмущающей силы (m2)
A(k ,k )
Периодические возмущения :
Amlp
T
1
2
k n k n
1
1
2 2
2
k n k n
1
1
2 2
Слайд 29
Метод Лагранжа или
метод оскулирующих элементов
•
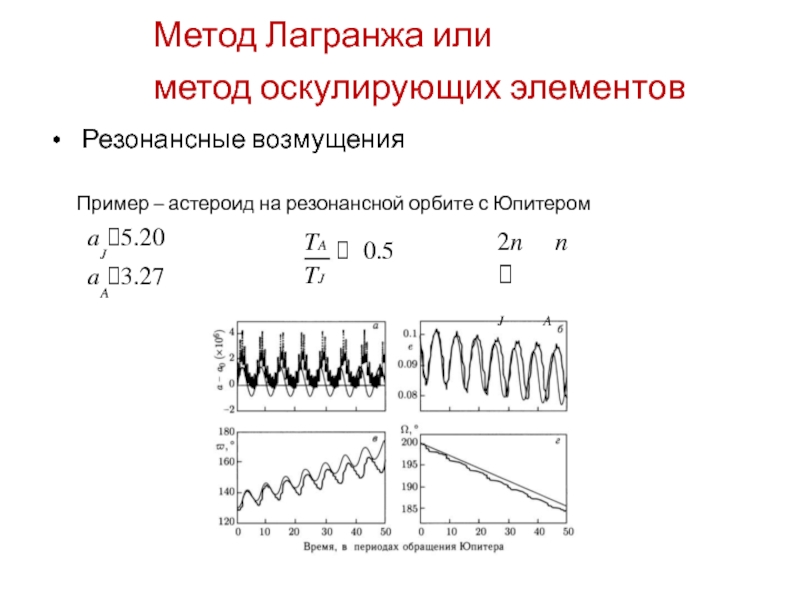
Резонансные возмущения
Пример – астероид на резонансной орбите
a 5.20
TA
TJ
2n n
J A
0.5
J
a 3.27
A
Слайд 30
Метод Лагранжа или
метод оскулирующих элементов
•
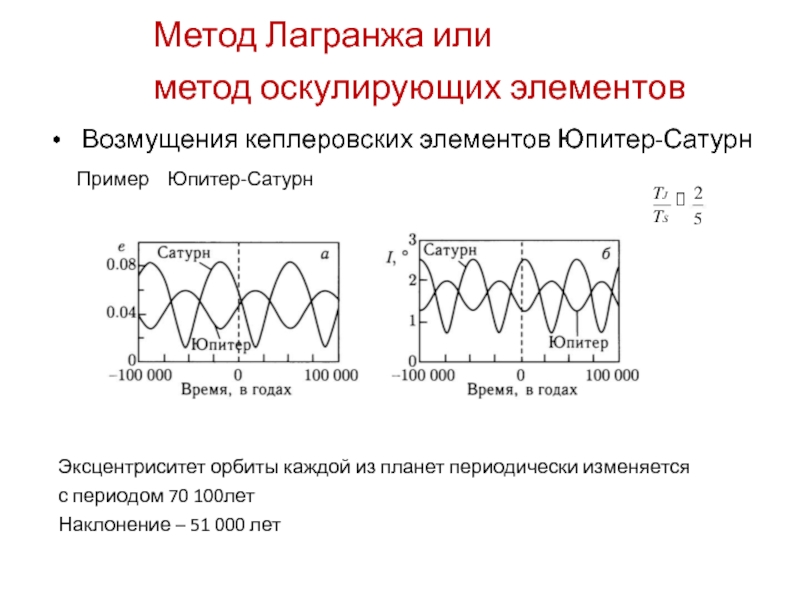
Возмущения кеплеровских элементов Юпитер-Сатурн
Пример Юпитер-Сатурн
TJ
TS
2
5
Эксцентриситет орбиты
с периодом 70 100лет
Наклонение – 51 000 лет
Слайд 31
Метод Лагранжа или
метод оскулирующих элементов
A(k ,k )
Amlp
1
2
•
Короткопериодические возмущения
k n k
1
1
2 2
2
k1n1
k n k n k n
1 1
T
1
1
2 2
Периоды возмущений порядка орбитального периода, амплитуда мала.
•
Долгопериодические возмущения (при малых k1,k2)
k n k n 0
Отношение средних движений =простой дроби
1
1
2 2
n k
1
2
1
- резонансное состояние
n k
2
Слайд 32
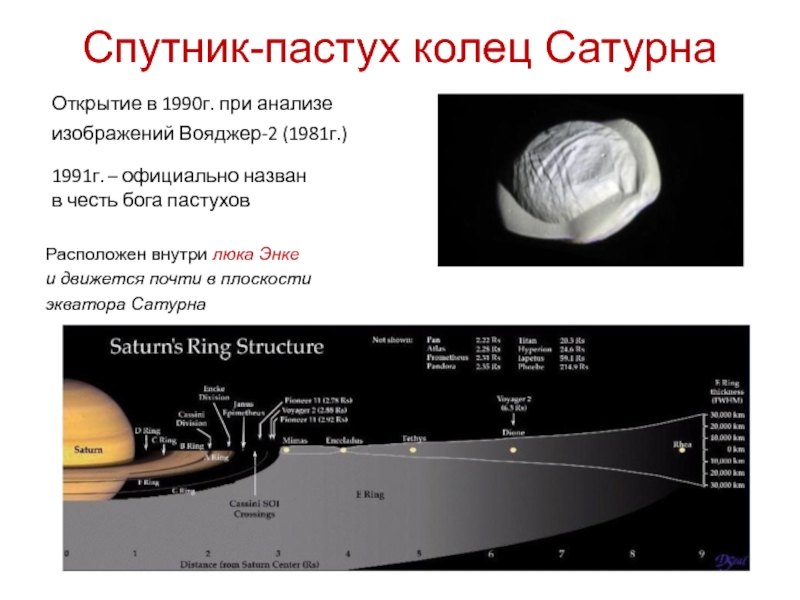
Спутник-пастух колец Сатурна
Открытие в 1990г. при анализе
изображений Вояджер-2 (1981г.)
1991г.
– официально назван
в
Расположен внутри люка Энке
и движется почти в плоскости
экватора Сатурна
Слайд 34
Спутники-пастухи
Cassini's confirmation that a small moon orbits within the Keeler gap
more exciting by this image, in which the disk of the 7 kilometer-wide body is resolved for the first
time.
The new body, provisionally named S/2005 S1, was first seen in a time-lapse sequence of images
taken on May 1, 2005, as Cassini began its climb to higher elevations in orbit around.
In the vicinity of the little moon, the Keeler gap edges bear striking similarities to the scalloped edges
of the 322 kilometer-wide Encke gap, where the small moon Pan (25 kilometers across) resides.
From the size of the waves seen in the scalloped edges of the Encke gap, imaging scientists were
able to estimate the mass of Pan. They expect to do the same eventually with S/2005 S1.
This image was obtained with the Cassini spacecraft narrow-angle camera on May 2, 2005, at a
distance of about 594,000 kilometers from Saturn.
https://www.nasa.gov/mission_pages/cassini/multimedia/pia06237.html
Слайд 36
Астероид Круитни
Орбитальный резонанс с Землей 1:1
Сопутствующая ситема к.
Проекция на эклиптику
Слайд 37
Сечение Пуанкаре
Сечение (отображение) Пуанкаре – отображение проекции
траектории на выделенную плоскость фазового
Для траектории на плоскости:
4-
х мерное фазовое пространство
x, y,x, y)
(
Одну из переменных можно исключить,
воспользовавшись интегралом Якоби
или полной энергией => 3D фазовое пр-во
(
x, y,x)
Выделяем одну из плоскостей, например, y=0 .
(
x,x)
Т.о. получаем проекцию на фазовую плоскость
Слайд 38
Сечение Пуанкаре
1
2
y y
3
Потенциал Хенона-Хейлиса
U(x, y)
2
y
2
2x
2
3
2
E =1/40
tot
N=50 – число частиц
150
периодов
Траектория одной из частиц
150
периодов
Слайд 39
Сечение Пуанкаре
Потенциал Хенона-Хейлиса
1
U(x, y) x
2
y
3
2
y
2
2x
2
3
2
N=50 – число частиц
a few 100 periods
E =1/40
tot