- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение правильных многоугольников презентация
Содержание
- 1. Построение правильных многоугольников
- 3. В геометрии выделяют задачи
- 4. Построение правильного шестиугольника, сторона которого равна данному
- 5. Построение правильного шестиугольника, сторона которого равна данному
- 6. Задача. Как, используя правильный шестиугольник построить правильный
- 7. Задача. Как, используя правильный шестиугольник построить правильный
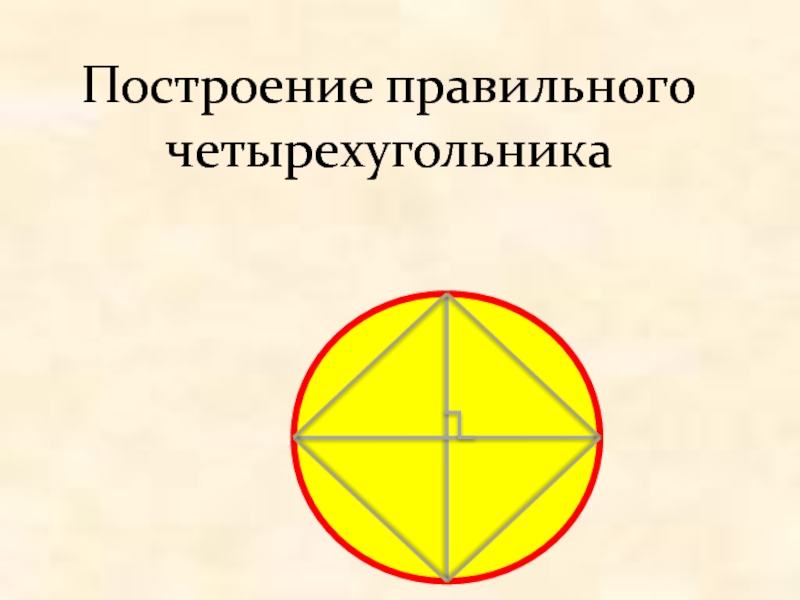
- 8. Построение правильного четырехугольника
- 11. Ап А1 А2
- 12. Построение правильных многоугольников, то есть деление окружности
- 13. Еще в глубокой древности была поставлена
- 14. Именно в школе ПИФАГОРА зародилось учение о
- 15. По некоторым источникам, он являлся автором сочинения
- 16. Описал построение правильных 3 ,
- 17. Развитие готического стиля и широкое применение витражей
- 18. Именно Альбрехт Дюрер осуществил новое построение
- 19. Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
- 20. Для своего друга Луки Пачоли Леонардо, глубоко
- 21. математик Иоганн Кеплер создал трактат «Новогодний подарок
- 22. Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться математикой, а не филологией.
- 23. Правильные многогранники
В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Линейка позволяет провести произвольную
Слайд 3 В геометрии выделяют задачи на построение, которые можно
решить только с помощью двух инструментов: циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую через две данные точки;
с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую через две данные точки;
с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Слайд 4Построение правильного шестиугольника, сторона которого равна данному отрезку.
Какая зависимость существует между
стороной правильного шестиугольника и радиусом описанной около него окружности?
Пусть РQ – заданный отрезок, равный стороне правильного шестиугольника, который нам необходимо построить. Чему равен радиус описанной около этого шестиугольника окружности?
Составьте план построения правильного шестиугольника со стороной РQ.
Пусть РQ – заданный отрезок, равный стороне правильного шестиугольника, который нам необходимо построить. Чему равен радиус описанной около этого шестиугольника окружности?
Составьте план построения правильного шестиугольника со стороной РQ.
Ответ: a6 = R
Ответ: PQ.
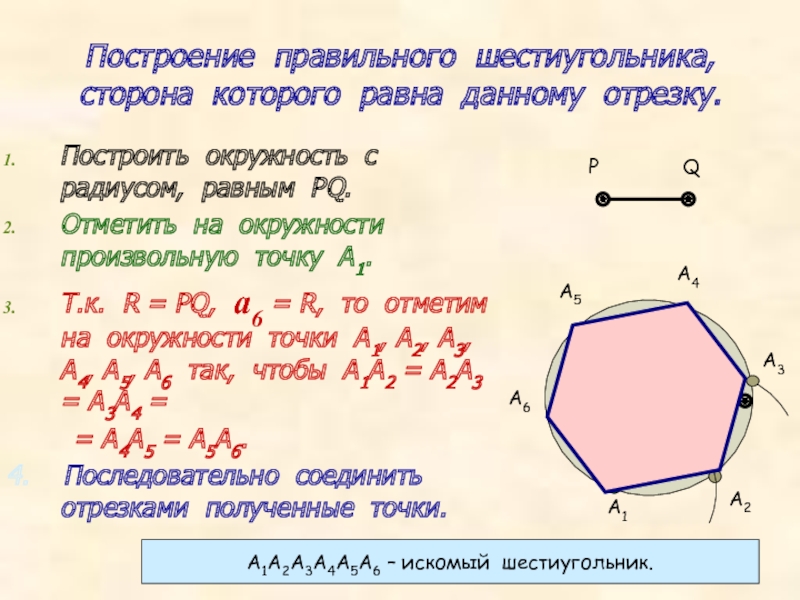
Слайд 5Построение правильного шестиугольника, сторона которого равна данному отрезку.
Построить окружность с радиусом,
равным PQ.
Отметить на окружности произвольную точку А1.
Т.к. R = PQ, а6 = R, то отметим на окружности точки А1, А2, А3, А4, А5, А6 так, чтобы А1А2 = А2А3 = А3А4 =
= А4А5 = А5А6.
4. Последовательно соединить отрезками полученные точки.
Отметить на окружности произвольную точку А1.
Т.к. R = PQ, а6 = R, то отметим на окружности точки А1, А2, А3, А4, А5, А6 так, чтобы А1А2 = А2А3 = А3А4 =
= А4А5 = А5А6.
4. Последовательно соединить отрезками полученные точки.
P
Q
А1
А2
А3
А1А2А3А4А5А6 – искомый шестиугольник.
А4
А5
А6
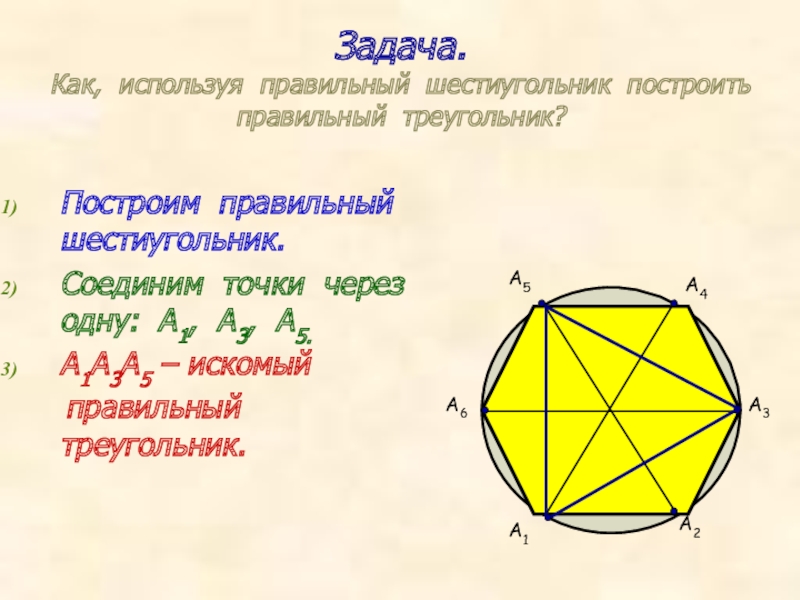
Слайд 6Задача.
Как, используя правильный шестиугольник построить правильный треугольник?
А1
А2
А3
А4
А5
А6
Построим правильный шестиугольник.
Соединим точки через
одну: А1, А3, А5.
А1А3А5 – искомый
правильный треугольник.
А1А3А5 – искомый
правильный треугольник.
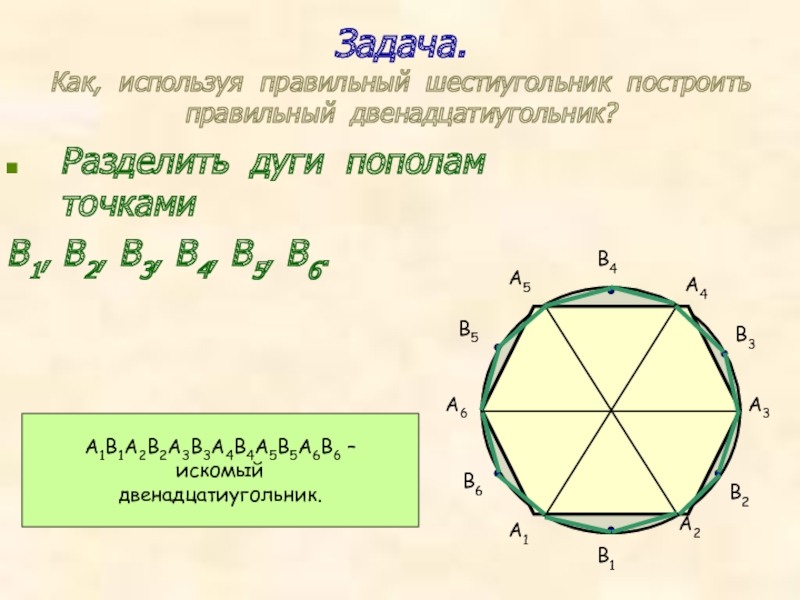
Слайд 7Задача.
Как, используя правильный шестиугольник построить правильный двенадцатиугольник?
Разделить дуги пополам точками
В1,
В2, В3, В4, В5, В6.
А1
А2
А3
А4
А5
А6
В1
В4
В2
В5
В3
В6
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
Слайд 11
Ап
А1
А2
О
Н1
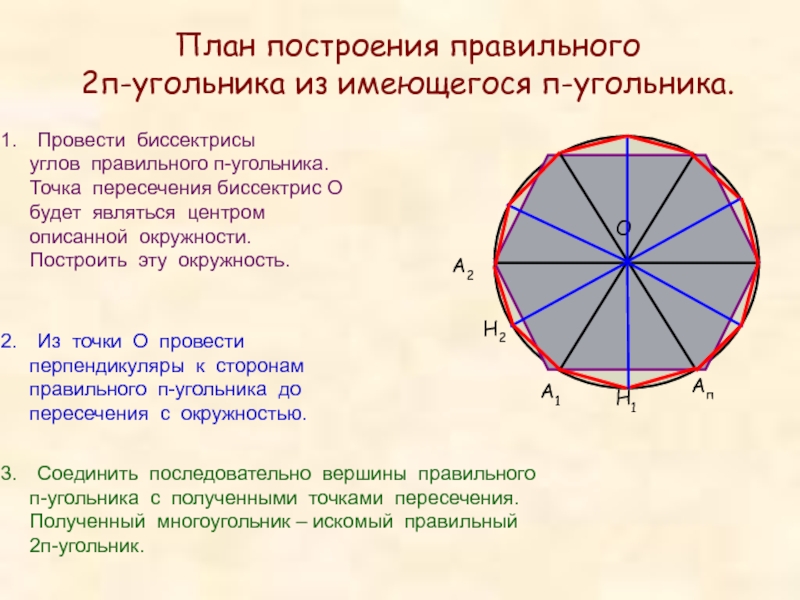
План построения правильного
2п-угольника из имеющегося п-угольника.
Провести биссектрисы
углов правильного
п-угольника.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
Точка пересечения биссектрис О
будет являться центром
описанной окружности.
Построить эту окружность.
Н2
Из точки О провести
перпендикуляры к сторонам
правильного п-угольника до
пересечения с окружностью.
Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
Слайд 12Построение правильных многоугольников, то есть деление окружности на равные части, позволяло
решать практические задачи:
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
4)Создание астрономических сооружений
1)Создание колеса со спицами;
2)Деление циферблата часов;
3)Строительство античных театров;
4)Создание астрономических сооружений
Слайд 13
Еще в глубокой древности была поставлена практическая задача построения правильного многоугольника
с помощью циркуля и линейки.
Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математиков XYII - XIX веков
Решение этой задачи можно найти в трудах древнегреческих ученых Архимеда, Евклида, Пифагора, математиков XYII - XIX веков
Слайд 14Именно в школе ПИФАГОРА зародилось учение о правильных многоугольниках; кроме того,
пифагорейцы рассмотрели вопрос покрытия плоскости правильными многоугольниками.
Слайд 15По некоторым источникам, он являлся автором сочинения о правильных многоугольниках, часто
присоединяемого к "Началам" в качестве XV книги. Исидор из Милета (532-537 гг.) - византийский архитектор и геометр, построивший вместе с Анфи - мием собор Святой Софии в Константинополе.
Слайд 17Развитие готического стиля и широкое применение витражей в строительстве соборов также
заставило вернуться к задачам построения правильных многоугольников.
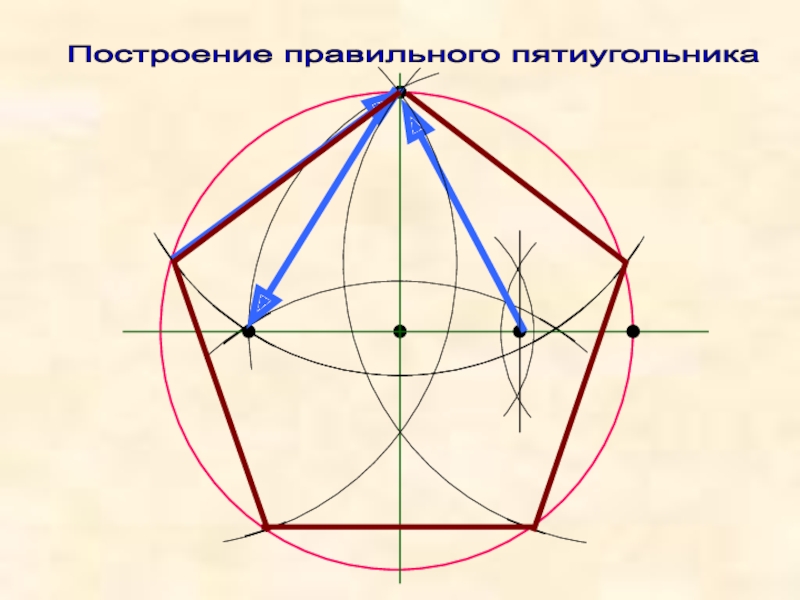
Слайд 18 Именно Альбрехт Дюрер осуществил новое построение правильного пятиугольника, передав потомкам
средневековый способ построения постоянным раствором циркуля.
Слайд 19Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений;
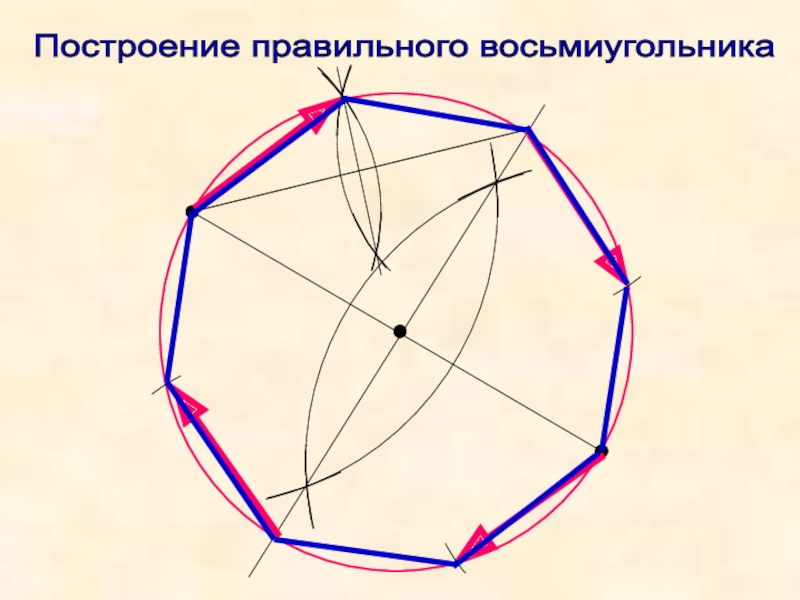
Решил задачу построения правильного восьмиугольника;
Разработал
принципы черчения художественно исполненных букв.
Слайд 20Для своего друга Луки Пачоли Леонардо, глубоко интересующийся пропорциями, создал иллюстрации
многогранников, гранями которых являются правильные многоугольники.
Слайд 21математик Иоганн Кеплер создал трактат «Новогодний подарок или о шестиугольных снежинках»,
опубликованный в 1611 году. В нем он практически привел первый пример разбиения плоскости на правильные шестиугольники.
Слайд 22Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться
математикой, а не филологией.
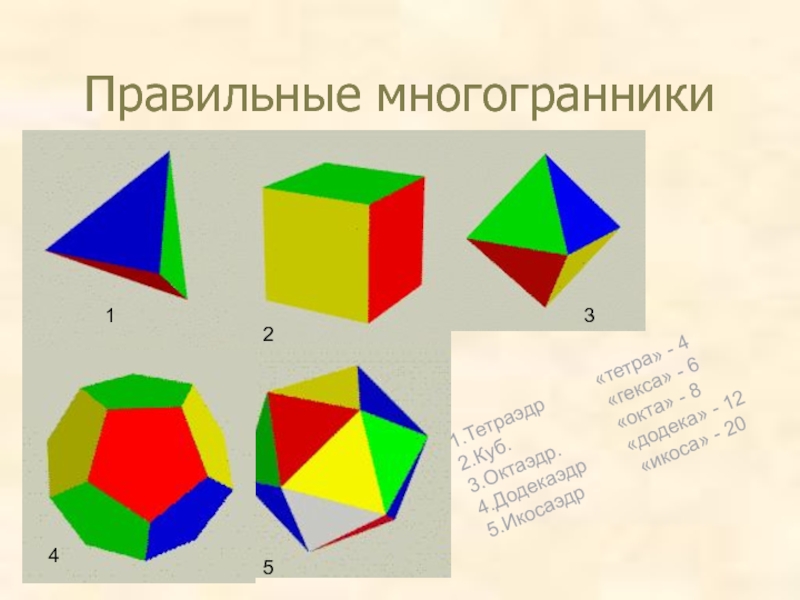
Слайд 23Правильные многогранники
1.Тетраэдр «тетра» - 4
2.Куб. «гекса» - 6
3.Октаэдр. «окта» - 8
4.Додекаэдр «додека» - 12
5.Икосаэдр «икоса» - 20
1
2
3
4
5
