- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение и выбор аналитических моделей презентация
Содержание
- 1. Построение и выбор аналитических моделей
- 2. ЧАСТЬ 1 Поиск аналитических зависимостей методом наименьших квадратов
- 3. Назначение и идея метода Назначение метода: Поиск
- 4. Иллюстрация к формуле (1.1) Формула (1.1)
- 5. ПРИМЕР 1 Поиск коэффициентов полинома. Пусть
- 6. Полученная на основании (1.2) система уравнений
- 7. ПОСЛЕДНИЙ ШАГ Система (1.3) решается относительно С1,
- 8. ЧАСТЬ 2 Решение системы линейных уравнений методом Гаусса
- 9. Форма представления исходных данных Метод
- 10. Исключение x1 из (n-1) уравнений Для этого
- 11. Компоненты системы (1.5)
- 12. Исключение xi в (n-i) уравнениях Для этого
- 13. Решение системы (1.6) Переменные системы (1.6) вычисляются
- 14. Пример 2 Поиск коэффициентов аналитической модели, описываемой экспонентой:
- 15. Преобразование уравнения (1.7) Логарифмируя, получим полином:
- 16. Сведение задачи к известному виду Таким образом,
- 17. Приравнивая нулю производные, получим систему (1.8):
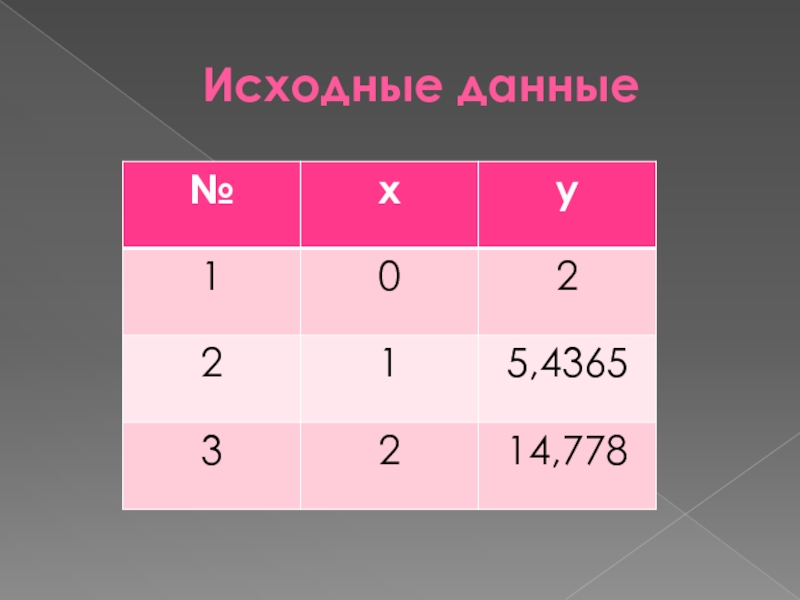
- 18. Исходные данные
- 19. Вид системы (1.8)
- 20. Решение системы (1.9)
- 21. САМОСТОЯТЕЛЬНО Поиск коэффициентов аналитической модели, описываемой уравнением
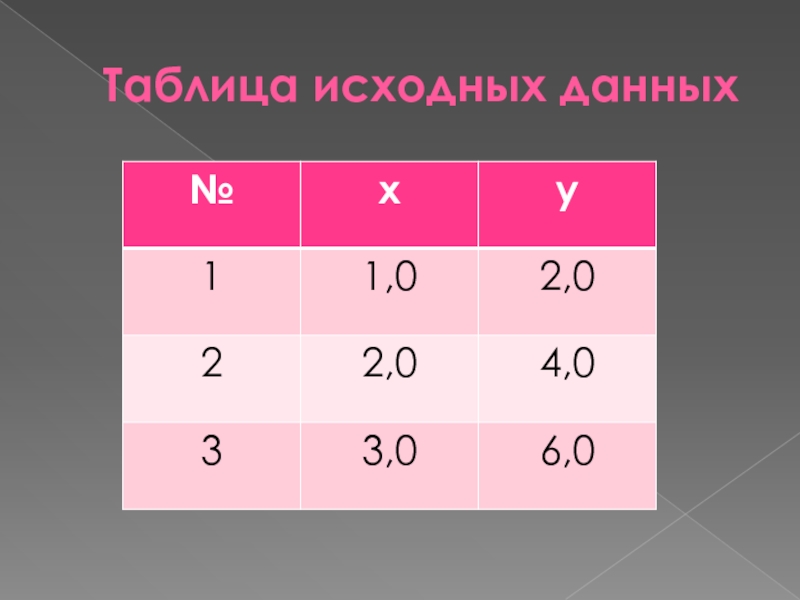
- 22. Таблица исходных данных
- 23. ЧАСТЬ 3 Выбор модели
- 24. Критерии качества аналитических моделей Максимальное по абсолютной
- 25. САМОСТОЯТЕЛЬНО Привести критерии качества аналитических моделей, отсутствующие на предыдущем слайде.
- 26. Графическая интерпретация Каждой аналитической модели у(x) можно
- 27. Сравнение интегрального критерия с эталоном
- 28. САМОСТОЯТЕЛЬНО Выбрать наилучшую из двух моделей:
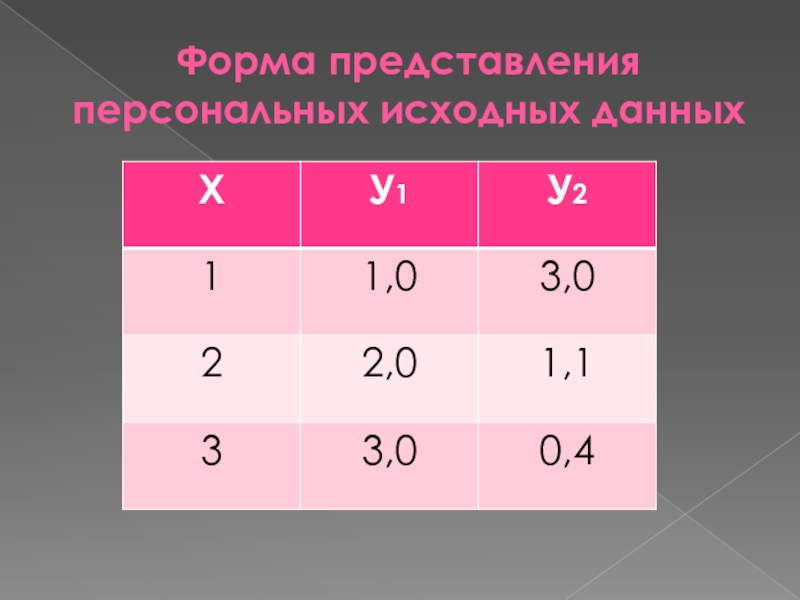
- 29. Форма представления персональных исходных данных
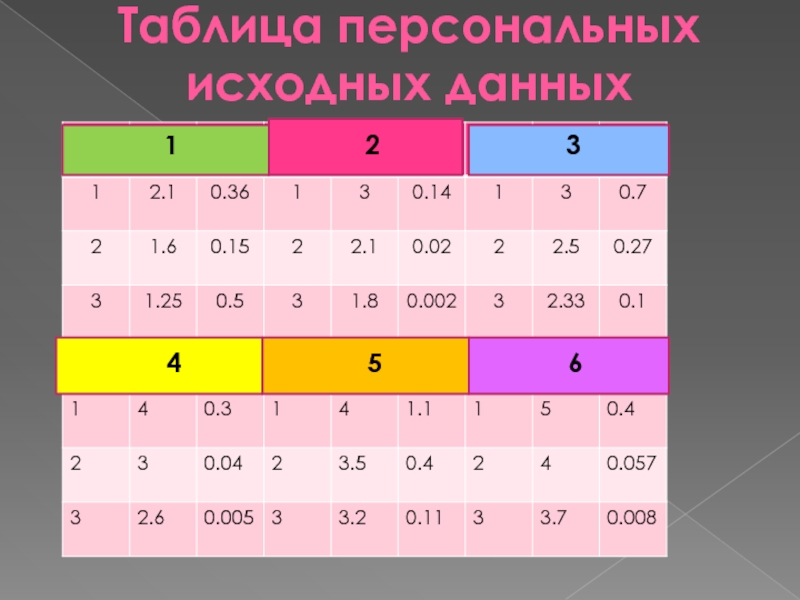
- 30. Таблица персональных исходных данных
- 31. Таблица персональных исходных данных
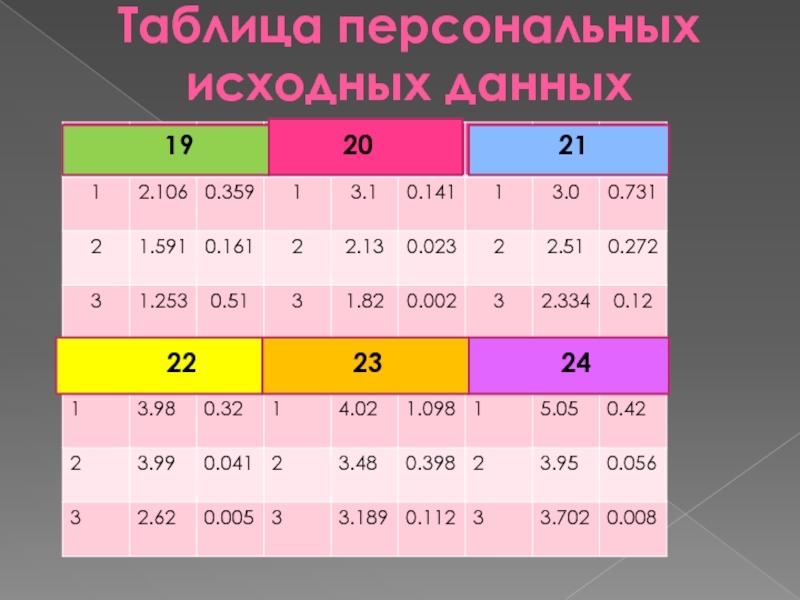
- 32. Таблица персональных исходных данных
- 33. Таблица персональных исходных данных
Слайд 3Назначение и идея метода
Назначение метода:
Поиск аналитической зависимости z = f(x) по
Идея метода
Полагаем известными:
а) предполагаемый вид исходной зависимости z = f(x);
б) таблицу, определяющую экспериментально полученную зависимость уi (xi), где i - номер эксперимента
Идея состоит в поиске коэффициентов функции z=f(x) которые бы минимизировали функцию S вида:
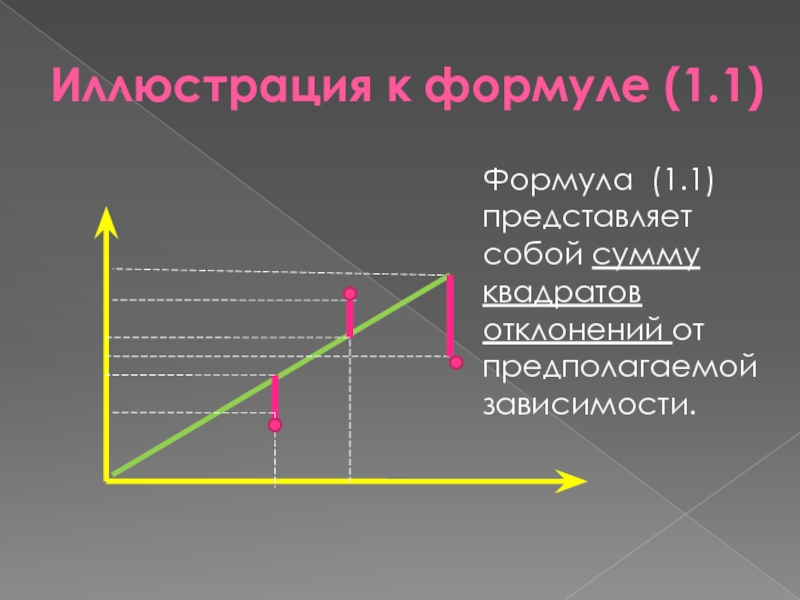
Слайд 4Иллюстрация к формуле (1.1)
Формула (1.1) представляет собой сумму квадратов отклонений
Слайд 5ПРИМЕР 1
Поиск коэффициентов полинома.
Пусть z(x) =c1 + c2x + c3x2
Слайд 7ПОСЛЕДНИЙ ШАГ
Система (1.3) решается относительно С1, С2, С3, что позволяет определить
Слайд 9Форма представления исходных данных
Метод основан на последовательном исключении неизвестных.
Слайд 10Исключение x1 из (n-1) уравнений
Для этого i-ое уравнение делится на ai1,
См. следующий слайд.
Слайд 12Исключение xi в (n-i) уравнениях
Для этого в (1.5) повторяется применительно к
Слайд 13Решение системы (1.6)
Переменные системы (1.6) вычисляются последовательно, начиная с xn. Т.о.
Слайд 16Сведение задачи к известному виду
Таким образом, задачу вновь удалось свести к
Слайд 21САМОСТОЯТЕЛЬНО
Поиск коэффициентов аналитической модели, описываемой уравнением вида:
Исходные данные представлены в таблице
Слайд 24Критерии качества аналитических моделей
Максимальное по абсолютной величине отклонение от экспериментальных данных.
Квадратичное
Среднее квадратичное отклонение - квадратный корнем из суммы квадратов такого рода отклонений деленный на число экспериментальных данных.
Сумма абсолютных величин отклонений от экспериментальных данных.
Среднее абсолютное отклонение- сумма абсолютных величин отклонений от экспериментальных данных, деленная на число экспериментальных данных.
Слайд 25САМОСТОЯТЕЛЬНО
Привести критерии качества аналитических моделей, отсутствующие на предыдущем слайде.
Слайд 26Графическая интерпретация
Каждой аналитической модели у(x) можно поставить в соответствие некоторую точку
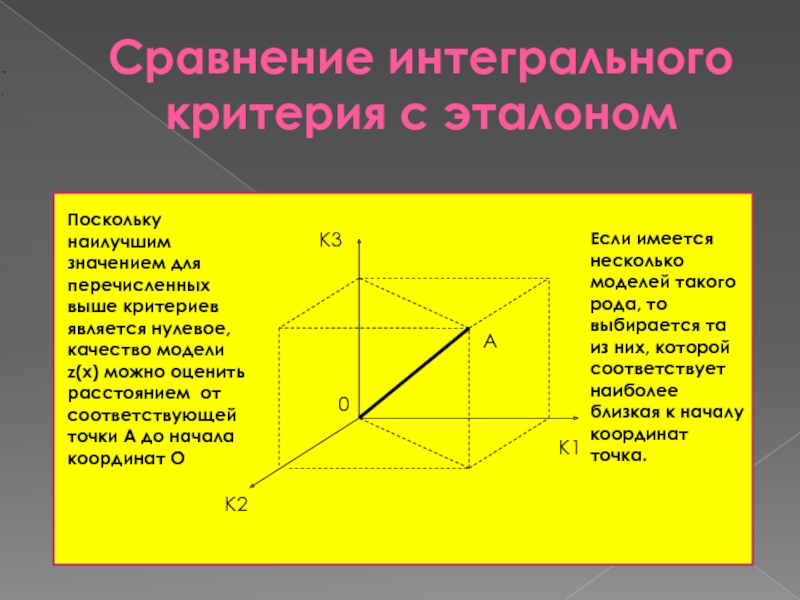
Слайд 27Сравнение интегрального критерия с эталоном
К3
К1
К2
0
А
Поскольку наилучшим значением для перечисленных выше
Если имеется несколько моделей такого рода, то выбирается та из них, которой соответствует наиболее близкая к началу координат точка.
Слайд 28САМОСТОЯТЕЛЬНО
Выбрать наилучшую из двух моделей:
если критериями являются максимальное отклонение и среднеквадратичное