Студента групи ПМ-12-1д
Бажана Станіслава
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лінійна крайова задача для звичайного диференціального рівняння другого порядку презентация
Содержание
- 1. Лінійна крайова задача для звичайного диференціального рівняння другого порядку
- 2. Бурхливий розвиток обчислювальної техніки у 50-60-х роках
- 3. Інженеру часто доводиться зіштовхуватись з диференційними рівняннями
- 4. ПОСТАНОВКА ЗАДАЧІ Завдання 1 Розв’язати з
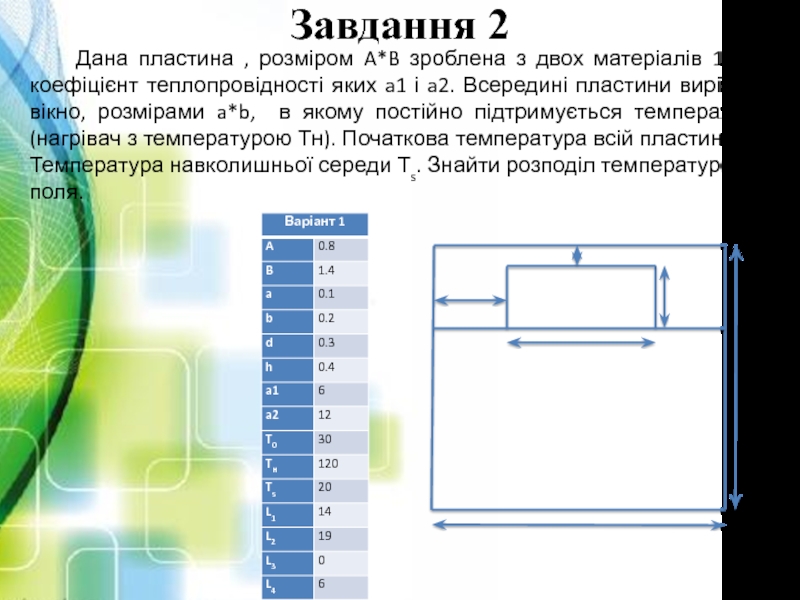
- 5. Завдання 2 Дана пластина , розміром
- 6. Рівняння, у якому невідома функція входить під знаком похідної чи диференціала, називається диференціальним рівнянням.
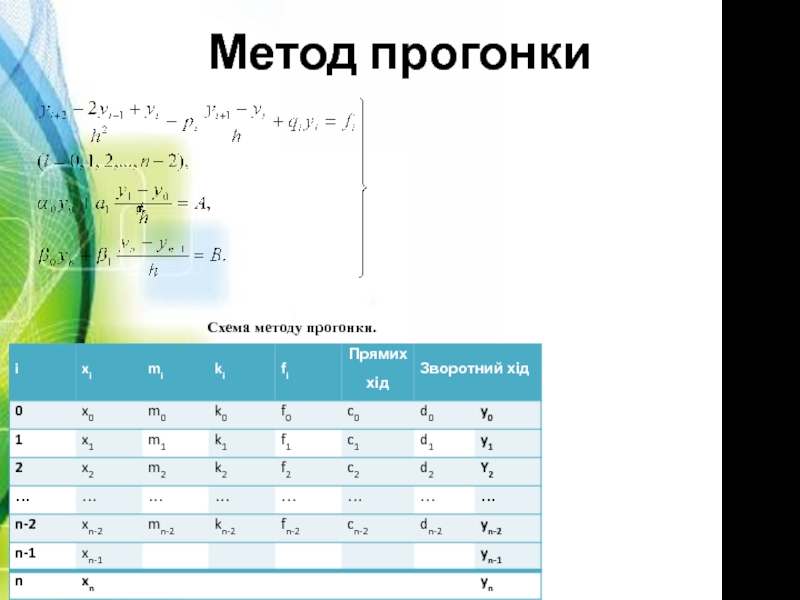
- 7. Методи розв’язку рівнянь: Метод стрільби; Метод прогонки; Метод зведення до задачі Коші; Різницевий метод.
- 8. Метод стрільби
- 9. Метод прогонки
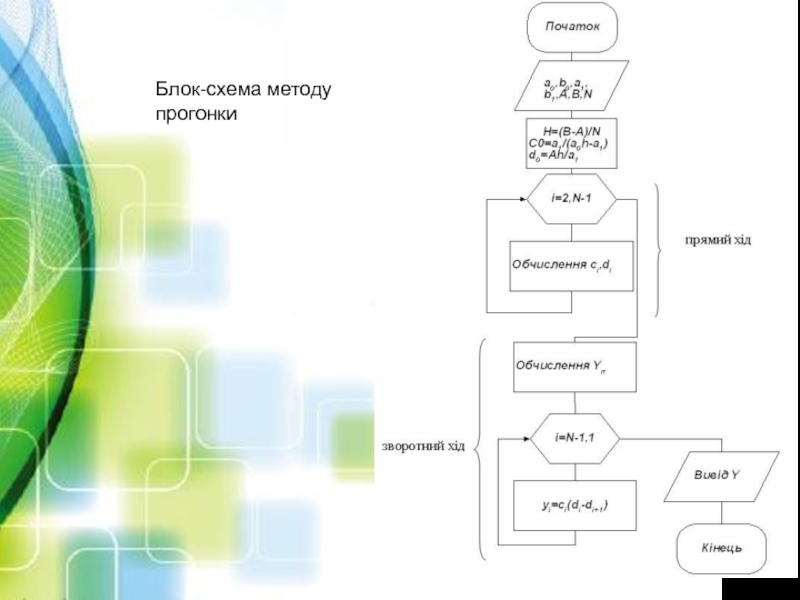
- 10. Блок-схема методу прогонки
- 11. Метод зведення до задачі Коші.
- 12. Різницевий метод
- 13.
- 14. Вирішення крайової задачі
- 15.
- 17. Двовимірна задача теплопровідності функції в
- 18.
- 19. Користуючись теоремою про збіжність різницевої
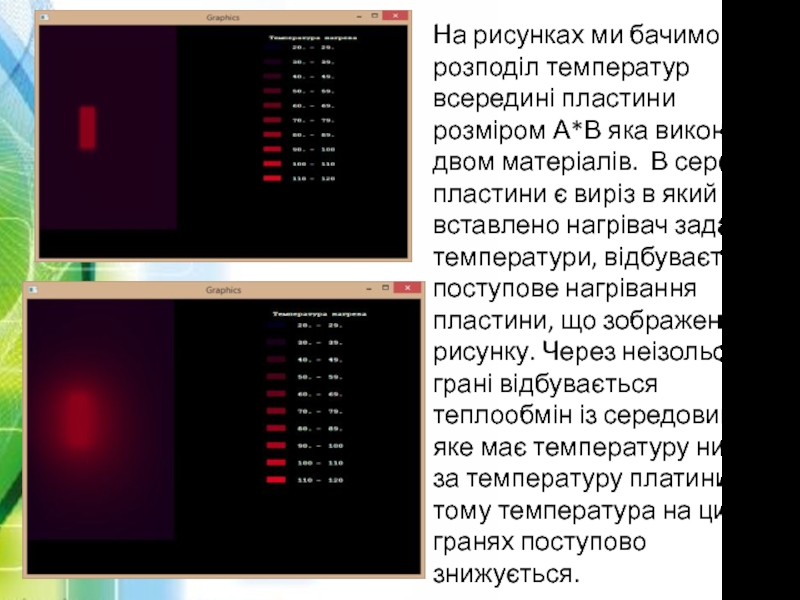
- 20. На рисунках ми бачимо розподіл температур всередині
- 21. ВИСНОВКИ Курсова робота виконана на тему «Лінійна
- 22. Дякую за увагу !
Слайд 1КУРСОВА РОБОТА з дисципліни «Методи обчислення» за темою: «Лінійна крайова задача для звичайного
диференціального рівняння другого порядку»
Слайд 2Бурхливий розвиток обчислювальної техніки у 50-60-х роках минулого століття наклав свій
відбиток на обчислювальну математику, предметом якої є чисельні методи та питання їх обґрунтування.
Слайд 3Інженеру часто доводиться зіштовхуватись з диференційними рівняннями і системами диференційних рівнянь
при розробці нових виробів чи технологічних процесів, так як більша частина законів фізики формалізується саме у вигляді диференційних рівнянь.
Слайд 4ПОСТАНОВКА ЗАДАЧІ
Завдання 1
Розв’язати з точністю 10-5 наступну крайову задачу:
y''=-fixy'-cosaxy+2x2+2x-4,
y0=0,
y1=0; a=0.7
Слайд 5Завдання 2
Дана пластина , розміром A*B зроблена з двох матеріалів 1
і 2, коефіцієнт теплопровідності яких a1 і a2. Всередині пластини вирізано вікно, розмірами a*b, в якому постійно підтримується температура (нагрівач з температурою Тн). Початкова температура всій пластини Т0. Температура навколишньої середи Тs. Знайти розподіл температурного поля.
Слайд 6Рівняння, у якому невідома функція входить під знаком похідної чи диференціала,
називається диференціальним рівнянням.
Слайд 7Методи розв’язку рівнянь:
Метод стрільби;
Метод прогонки;
Метод зведення до задачі Коші;
Різницевий метод.
Слайд 17Двовимірна задача теплопровідності
функції в двох крайніх вузлах різницевої сітки, виглядає наступним
чином:
;
.
Слайд 19
Користуючись теоремою про збіжність різницевої задачі, маємо, що із апроксимації і
стійкості слідує збіжність.
Слайд 20На рисунках ми бачимо розподіл температур всередині пластини розміром А*В яка
виконана з двом матеріалів. В середині пластини є виріз в який вставлено нагрівач заданої температури, відбувається поступове нагрівання пластини, що зображено на рисунку. Через неізольовані грані відбувається теплообмін із середовищем яке має температуру нижчу за температуру платини, тому температура на цих гранях поступово знижується.
Слайд 21ВИСНОВКИ
Курсова робота виконана на тему «Лінійна крайова задача для звичайного диференціального
рівняння другого порядку ». В даній роботі було розглянуто основні поняття про диференційні рівняння та теоретичні відомості. Також були описанні методи рішення параболічних рівнянь в приватних похідних. Був розглянутий приклад рішення крайової задачі для диференціального рівняння другого порядку та змодельоване його рішення, та були отримані певні результати, описані вище.
Також у курсовій роботі було розглянуто і з модельовано процес нагрівання пластини складної конфігурації з початковими даними. Комп’ютерна реалізація даної задачі дала нам певні розрахунки, які підтвердили, що з часом температура у пластині стає стаціонарною.
Також у курсовій роботі було розглянуто і з модельовано процес нагрівання пластини складної конфігурації з початковими даними. Комп’ютерна реалізація даної задачі дала нам певні розрахунки, які підтвердили, що з часом температура у пластині стає стаціонарною.