- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поняття функції. Загальні властивості функцій презентация
Содержание
- 1. Поняття функції. Загальні властивості функцій
- 2. План. Поняття функції. Способи задання. Загальні властивості
- 3. Означення функції Функція – це залежність
- 4. Функцію позначають: латинськими буквами f,
- 5. Способи задання функції таблицею графіком
- 6. Результати вимірювання температури тіла хворого в залежності
- 7. Графіком функції у = f(х) називається множина
- 8. Числовою функцією з областю визначення D називається
- 9. Існує декілька основних видів функцій: лінійна функція;
- 10. Область визначення функції у = f(х), яка
- 11. Для функцій, графіки, яких зображено, вкажіть D(y) і E(y)
- 12. 1) Якщо f(x) = P(x), де Р(х)-
- 13. Приклад. Знайти область визначення функції 1)
- 14. Для наступних функцій знайдіть D( f )
- 15. Функція у = f(х) називається парною, якщо
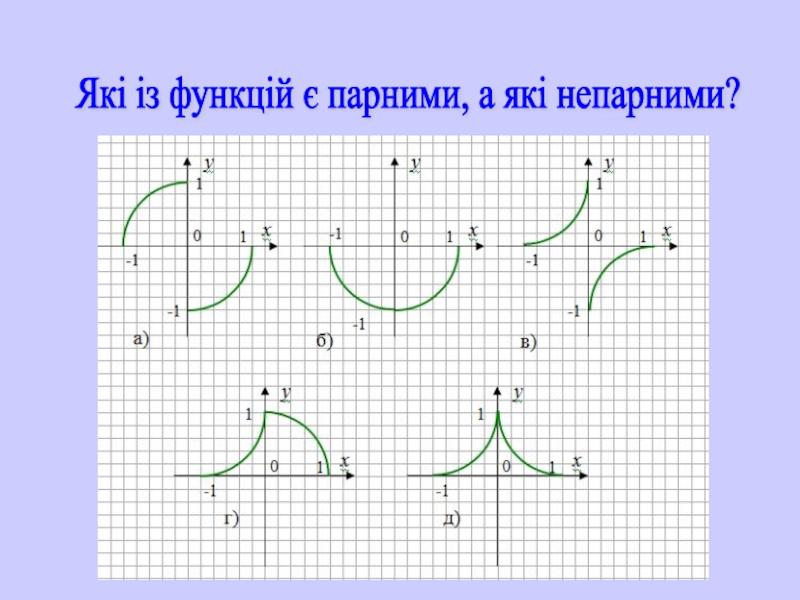
- 16. Які із функцій є парними, а які непарними?
- 17. Функція у = f(х) називається зростаючою, якщо
- 18. Монотонність функцій Функція у = f(х)
- 19. Користуючись графіками функцій, вкажіть проміжки зростання і спадання функцій
- 20. Взаємно обернені функції Дві функції f(х) та
- 21. Графіки взаємно обернених функцій Графіки функції f(х)
- 22. Властивості взаємно обернених функцій Якщо f(х) та
- 23. функция вида y = k х
- 24. Лінійна функція функція виду y
- 25. Зворотня пропорційність функція виду y
- 26. Квадратична функція функція виду y
- 27. функція виду y = x³;
- 28. функція виду y = ;
- 29. функція виду y = |x|; 1.
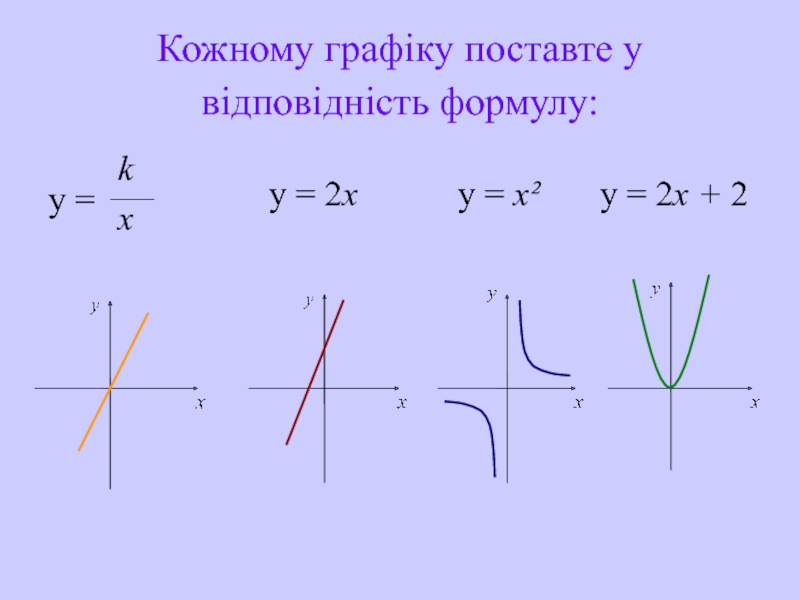
- 30. Кожному графіку поставте у відповідність формулу:
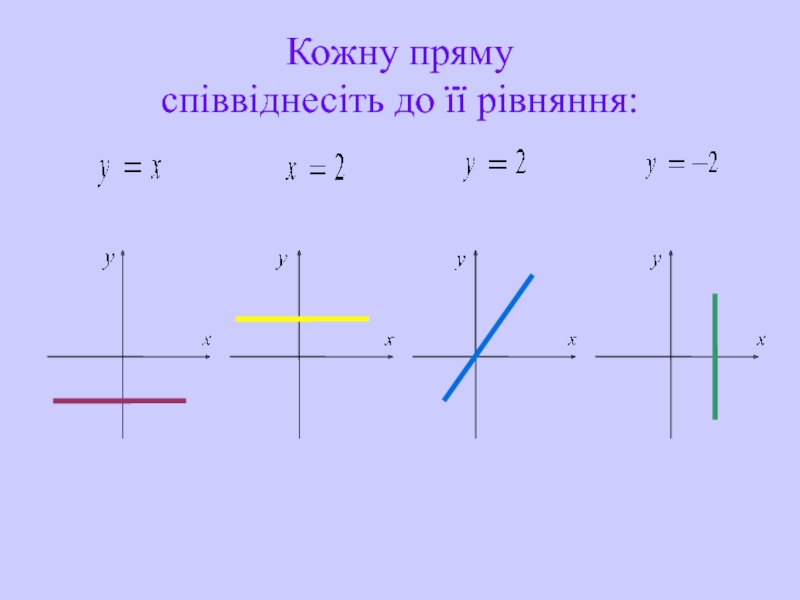
- 31. Кожну пряму співвіднесіть до її рівняння:
- 32. Домашнє завдання 1. Вивчити означення
Слайд 2План.
Поняття функції. Способи задання.
Загальні властивості функцій:
2.1. Область визначення.
2.2. Область значень.
2.3.
2.4. Нулі функції.
2.5. Проміжки монотонності.
Поняття оберненої функції, її графік.
Література.
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник), 10-11 кл. – К.: Зодіак – ЕКО, 2002.
Бевз Г.П. Алгебра і початки аналізу (підручник для шкіл, ліцеїв, гімназій гуманітарного напряму), 10-11 кл. – К.: ТОВ «Бліц», 2005
Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Дидактичні матеріали з математики (навчальний посібник для студентів ВНЗ І-ІІ р.а.) – К.: Вища школа, 2001
Слайд 3Означення функції
Функція – це залежність змінної у від змінної х,
х – незалежна змінна або аргумент функції
у – залежна змінна або функція
Слайд 4Функцію позначають:
латинськими буквами
f, g, h... (або f(х), g(х), h(х)...)
рівностями у = f(х), у = g(х), у = h(х)...
Приклад 1. у = 2х + 3 або f(х) = 2х + 3
Якщо задане конкретне значення незалежної змінної х=х0, то у0 = f(х0) називається значенням функції f в точці х0.
Приклад 2.
1. х = 5, то f(5) = 2∙ 5 + 3=10 + 3 = 13
2. f(х) = 0, тоді 2х + 3 = 0
2х = -3
х = -1,5
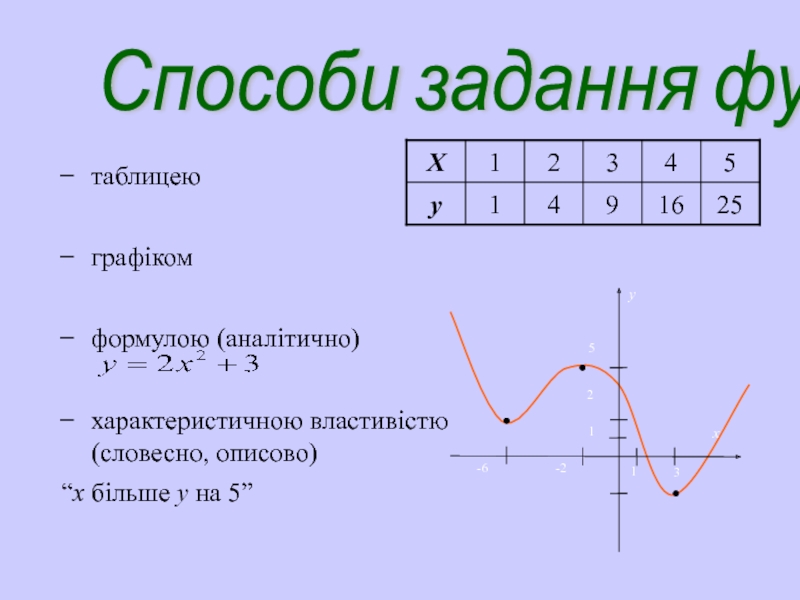
Слайд 5Способи задання функції
таблицею
графіком
формулою (аналітично)
характеристичною властивістю (словесно, описово)
“х більше
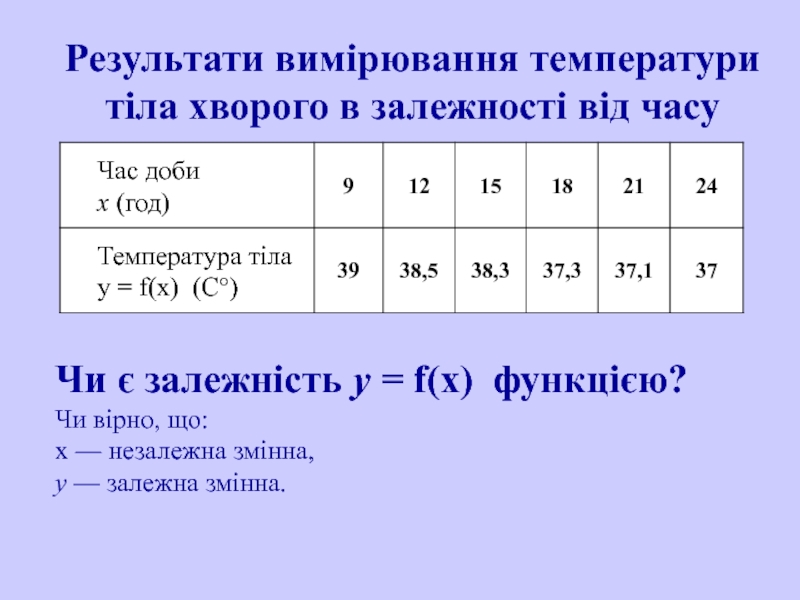
Слайд 6Результати вимірювання температури тіла хворого в залежності від часу
Чи є
Чи вірно, що:
х — незалежна змінна,
у — залежна змінна.
Слайд 7Графіком функції у = f(х) називається множина всіх точок площини з
Графік функції
X
Y
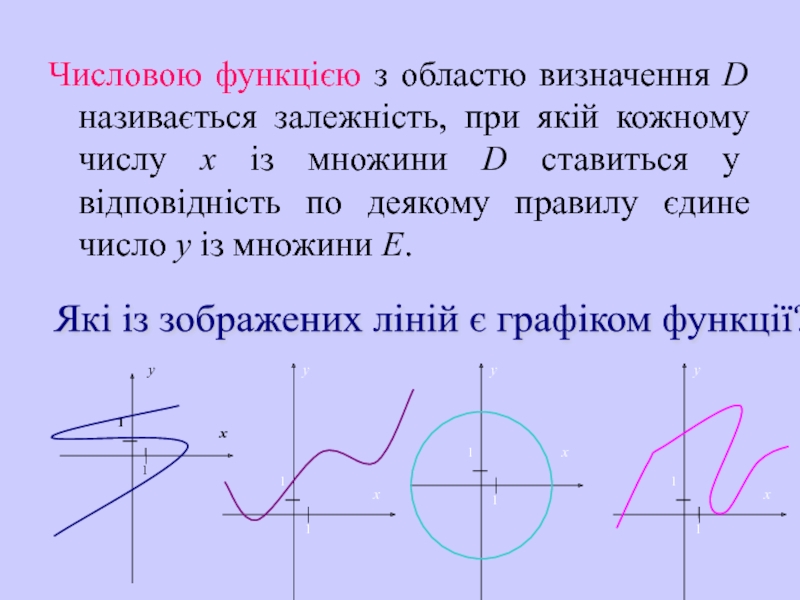
Слайд 8Числовою функцією з областю визначення D називається залежність, при якій кожному
Які із зображених ліній є графіком функції?
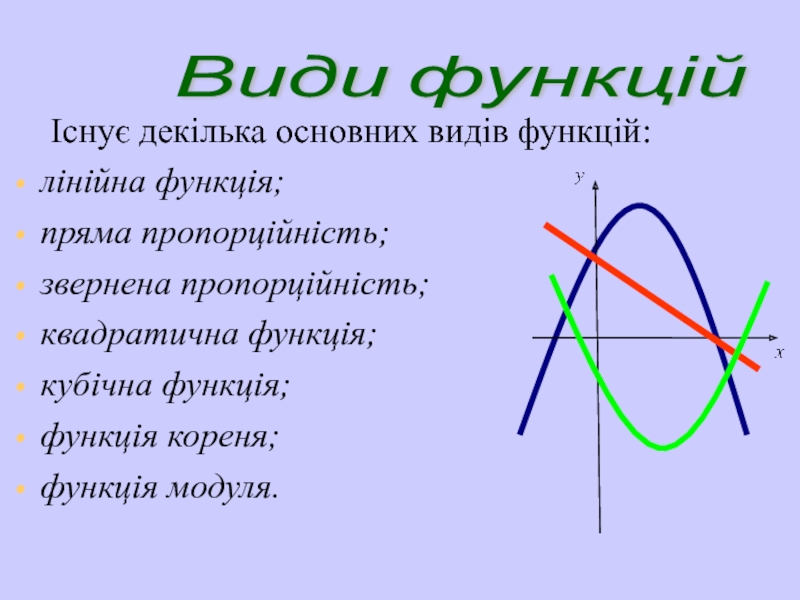
Слайд 9 Існує декілька основних видів функцій:
лінійна функція;
пряма пропорційність;
звернена пропорційність;
квадратична функція;
кубічна функція;
функція кореня;
функція
Види функцій
Слайд 10Область визначення функції у = f(х), яка задана формулою, називається множина
Позначення: D( f )
Множина, яка складається із всіх чисел f(х) таких, що х належить області визначення функції f, називається областю значень функції.
Позначення: Е( f )
Слайд 121) Якщо f(x) = P(x), де Р(х)- многочлен,
ціла
то D (у) = (-∞; +∞) = R
2) Якщо F(x) - дробова функція,
де f(х) і g(х) — многочлени,
то слід вважати g(х)≠ 0
(знаменник дробу не дорівнює 0).
3) Якщо функція ірраціональна , то слід вважати f(х)≥ 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).
При знаходженні області визначення
слід пам'ятати:
Слайд 13Приклад. Знайти область визначення функції
1) f (х) = 2х + 3
D(f)=R або D(f) = (- ; + )
2) f(х) = х +
2
3
x
D(f)=R або D(f) = (- ; + )
3) f(х) =
5x + 2
x - 8
D(f)= (- ; 8) (8; + )
х – 8 0
х 8
8
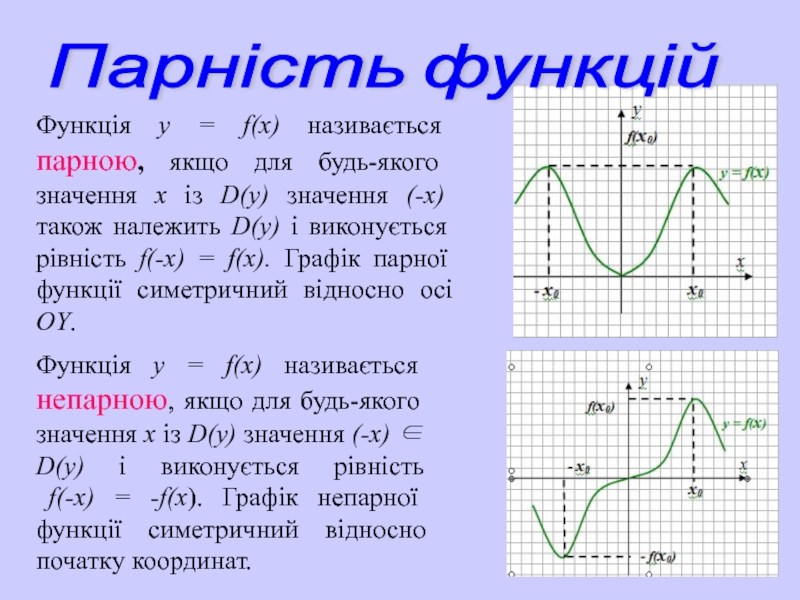
Слайд 15Функція у = f(х) називається парною, якщо для будь-якого значення х
Функція у = f(х) називається непарною, якщо для будь-якого значення х із D(у) значення (-х) ∈ D(у) і виконується рівність
f(-х) = -f(х). Графік непарної функції симетричний відносно початку координат.
Парність функцій
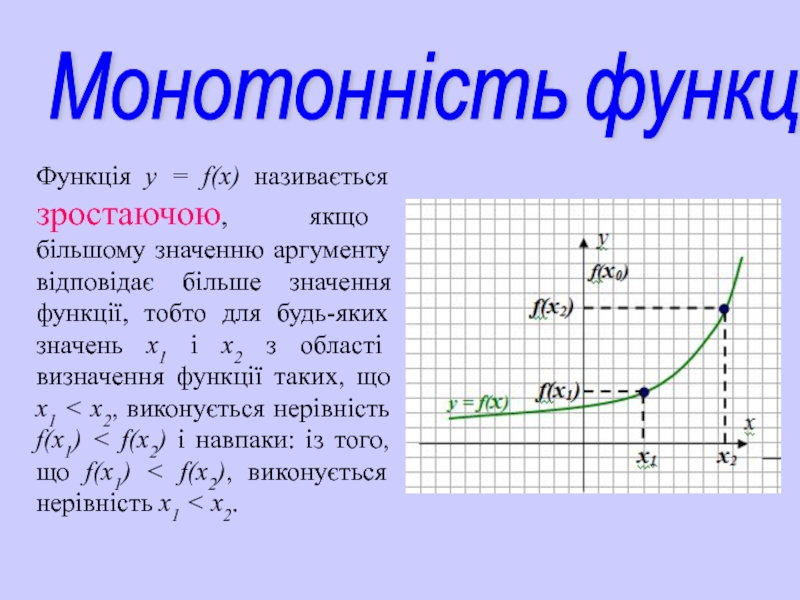
Слайд 17Функція у = f(х) називається зростаючою, якщо більшому значенню аргументу відповідає
Монотонність функцій
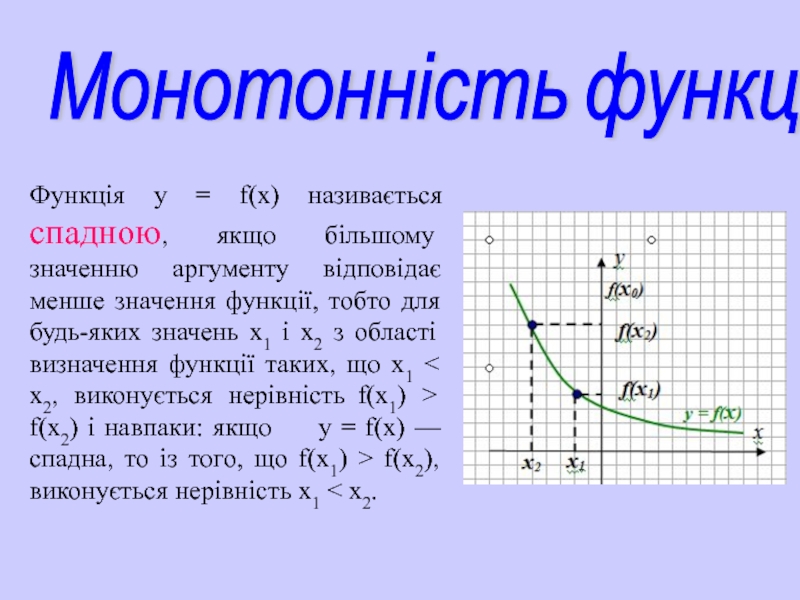
Слайд 18
Монотонність функцій
Функція у = f(х) називається
спадною, якщо більшому значенню аргументу відповідає
Слайд 20Взаємно обернені функції
Дві функції f(х) та g(y) називаються взаємно оберененими, якщо
у= f(х) х= g(y)
Функція має обернену, якщо функція строго зростає або строго спадає (строго монотонна).
Що отримати обернену функцію від деяких функцій, зменшують область визначення так, щоб область значень функції не змінилася.
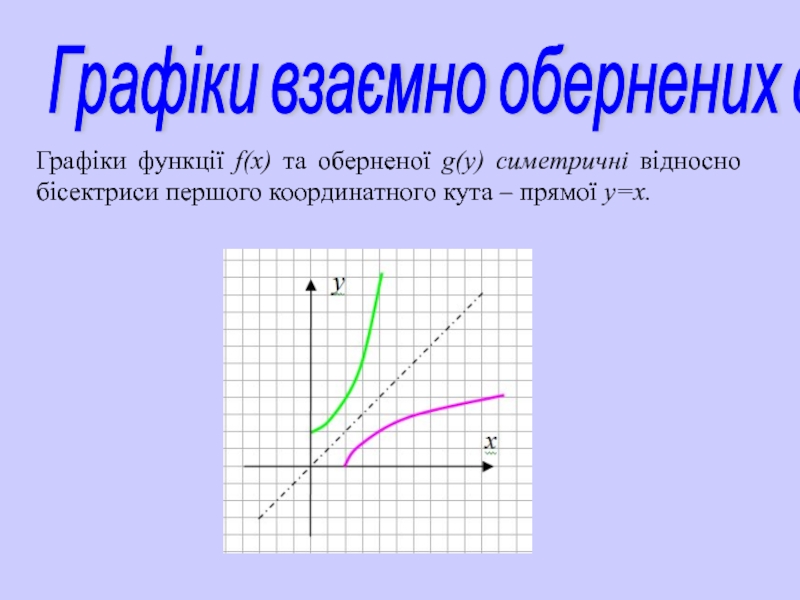
Слайд 21Графіки взаємно обернених функцій
Графіки функції f(х) та оберненої g(y) симетричні відносно
Слайд 22Властивості взаємно обернених функцій
Якщо f(х) та g(y) обернені функції, то область
Якщо одна з взаємно обернених функцій строго зростає, то і друга строго зростає.
Слайд 23 функция вида y = k х
1) D( f ) =
2) E( f ) = R;
3) Графіком функції є пряма лінія, яка проходить через початок координат.
Пряма пропорційність
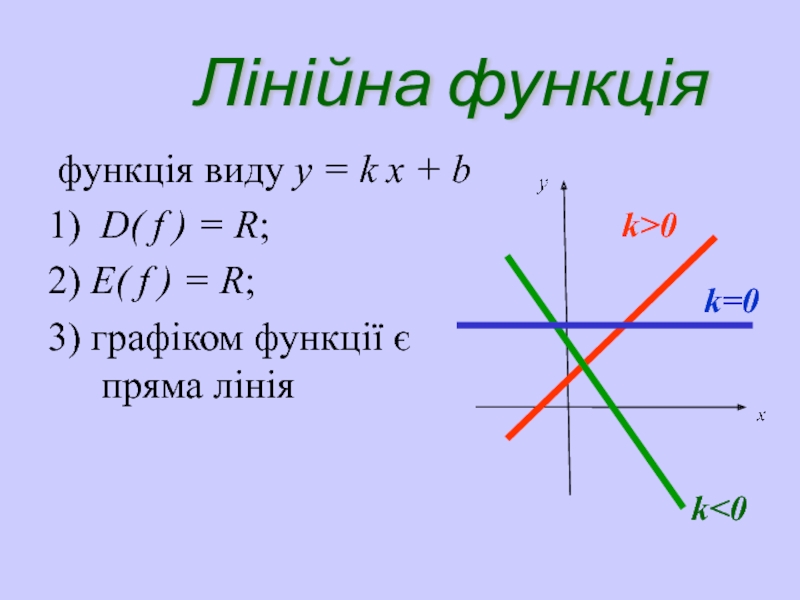
Слайд 24Лінійна функція
функція виду y = k х + b
1)
2) E( f ) = R;
3) графіком функції є пряма лінія
k>0
k<0
k=0
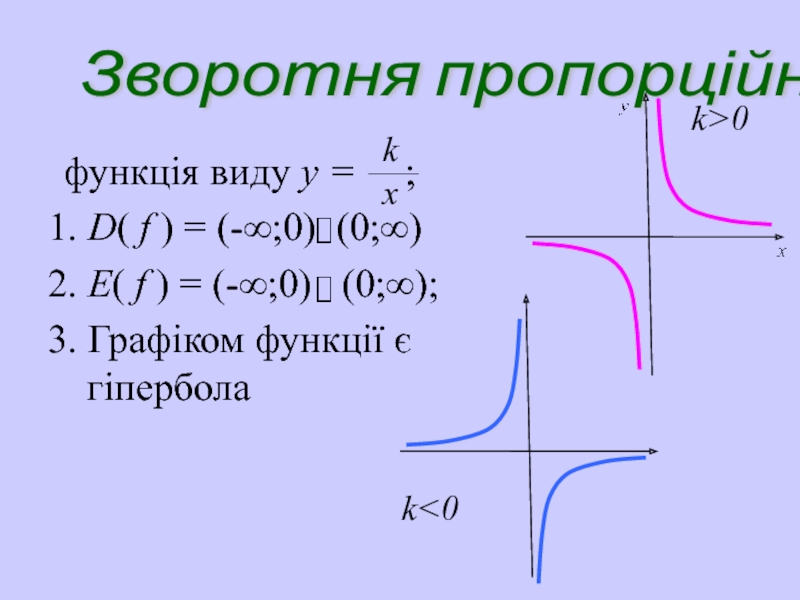
Слайд 25Зворотня пропорційність
функція виду y = ;
1.
2. E( f ) = (-∞;0) (0;∞);
3. Графіком функції є гіпербола
k
x
k>0
k<0
Слайд 26Квадратична функція
функція виду y = x² ;
D( f
2. E( f ) = [0;∞);
3. Графіком функції є парабола
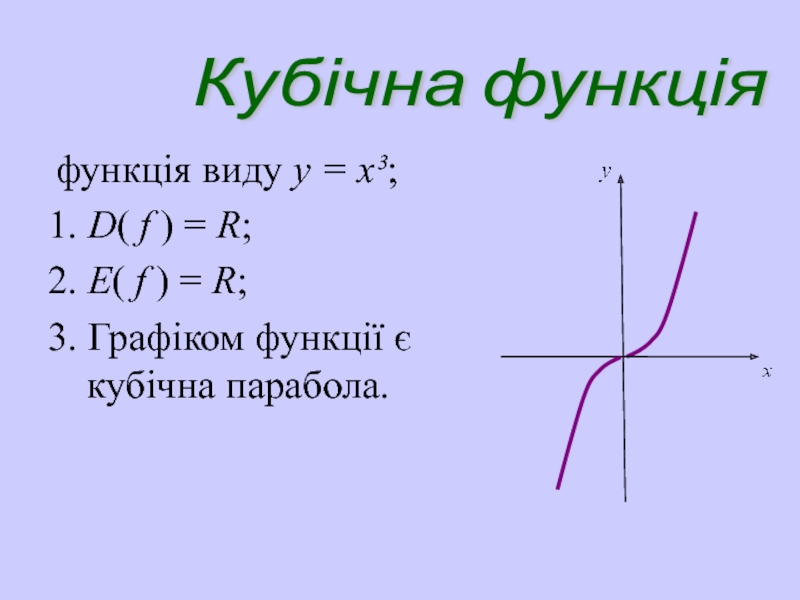
Слайд 27 функція виду y = x³;
1. D( f ) =
2. E( f ) = R;
3. Графіком функції є кубічна парабола.
Кубічна функція
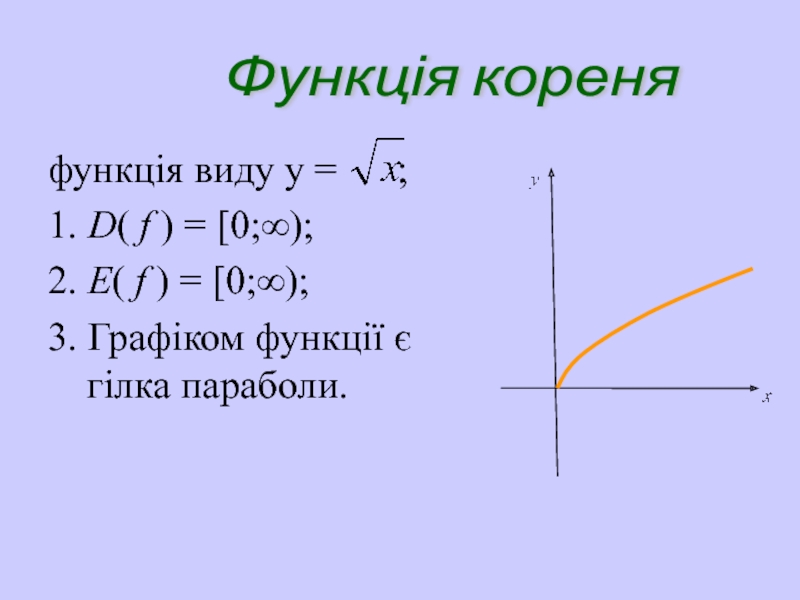
Слайд 28функція виду y = ;
1. D( f )
2. E( f ) = [0;∞);
3. Графіком функції є гілка параболи.
Функція кореня
Слайд 29функція виду y = |x|;
1. D( f ) = R;
2. E( f ) = [0;+∞);
3. Графік функції на проміжку [0;+∞) збігається з графіком функції у = х, а на проміжку (-∞;0] – з графіком функції у = -х
Функція модуля
Слайд 32Домашнє завдання
1. Вивчити означення за конспектом.
2. За підручником:
прочитати стор.
виконати завдання стор. 25-26 № 1 (1, 5, 8), № 2 (1, 3)
додаткові завдання стор. 25-26 № 1 (9, 14), № 2 (11, 18)