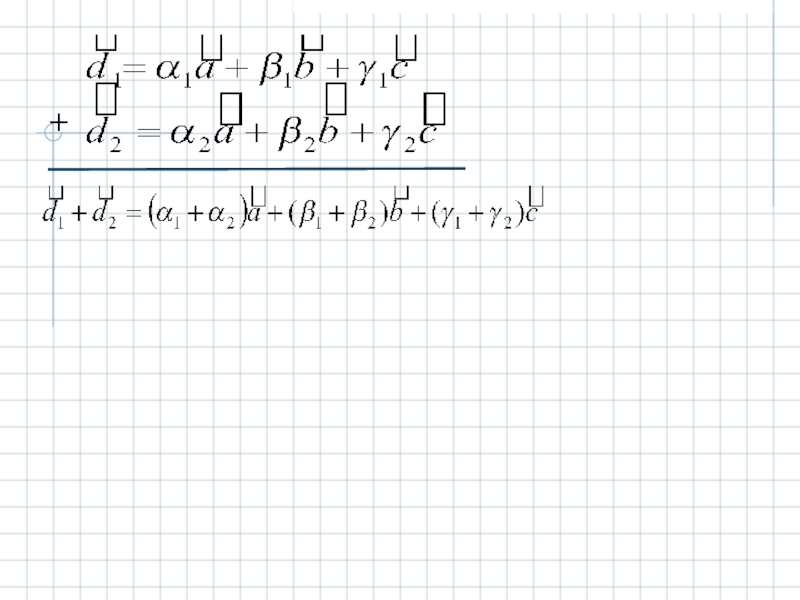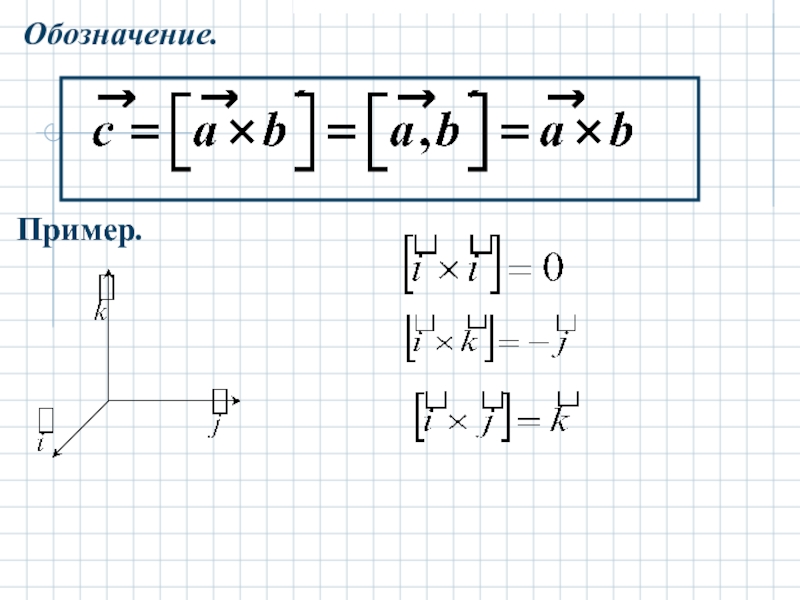- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторная алгебра презентация
Содержание
- 1. Векторная алгебра
- 2. Лекция 4 Векторная алгебра 2.
- 3. Вектор – направленный отрезок;
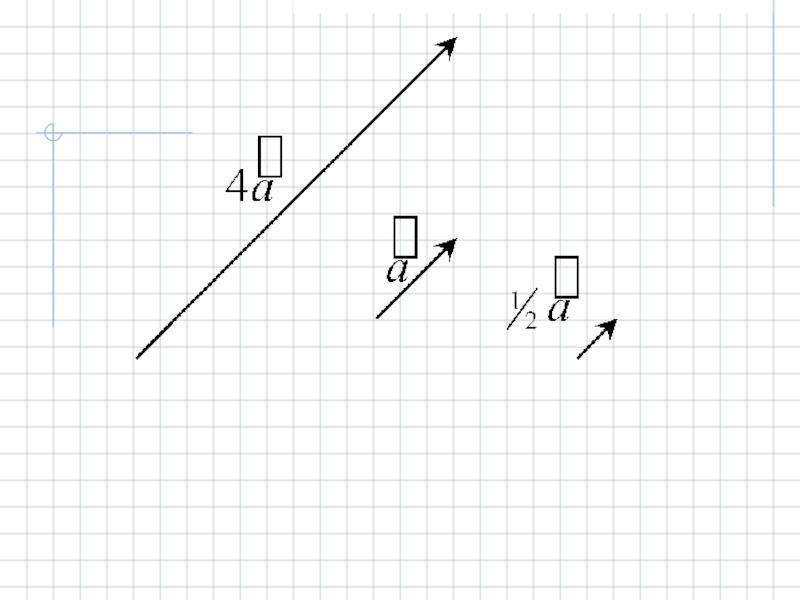
- 4. 2. Умножение вектора на число.
- 6. Свойства линейных операций над векторами.
- 7. Линейная зависимость (ЛЗ)
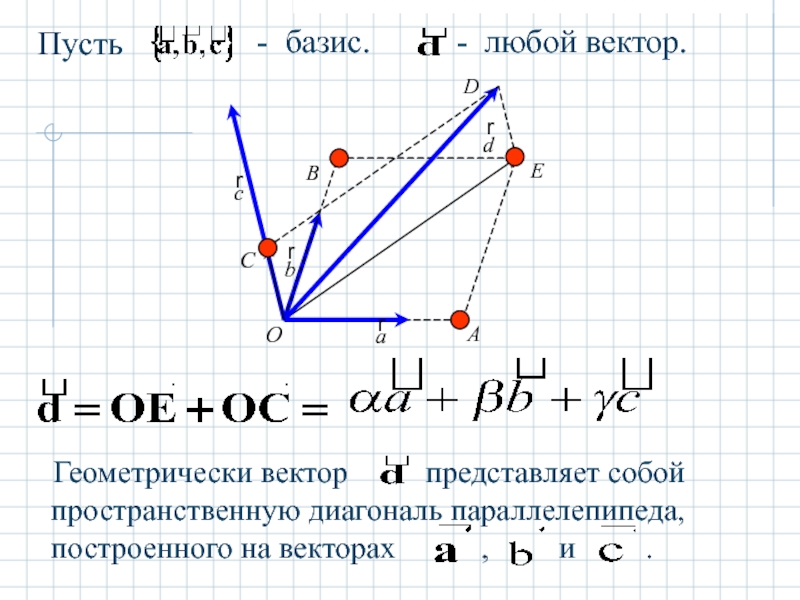
- 8. Базисом множества векторов на
- 9. Базисом множества векторов в пространстве называются любые три некомпланарных вектора.
- 11. Можно использовать такую запись:
- 12. Следствие. Два вектора, заданные в одном и том же базисе
- 13. I.Сложение. то Доказательство.
- 15. II. Умножение вектора на число. то
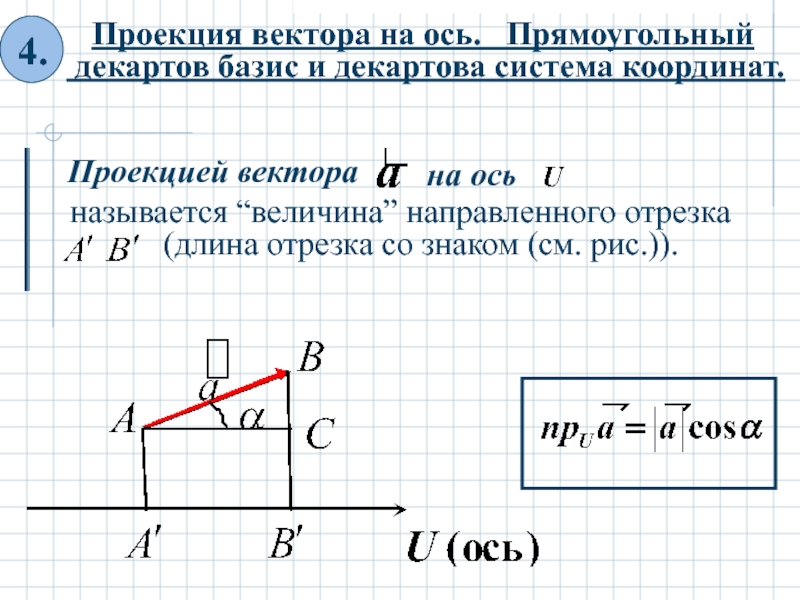
- 16. называется “величина” направленного отрезка
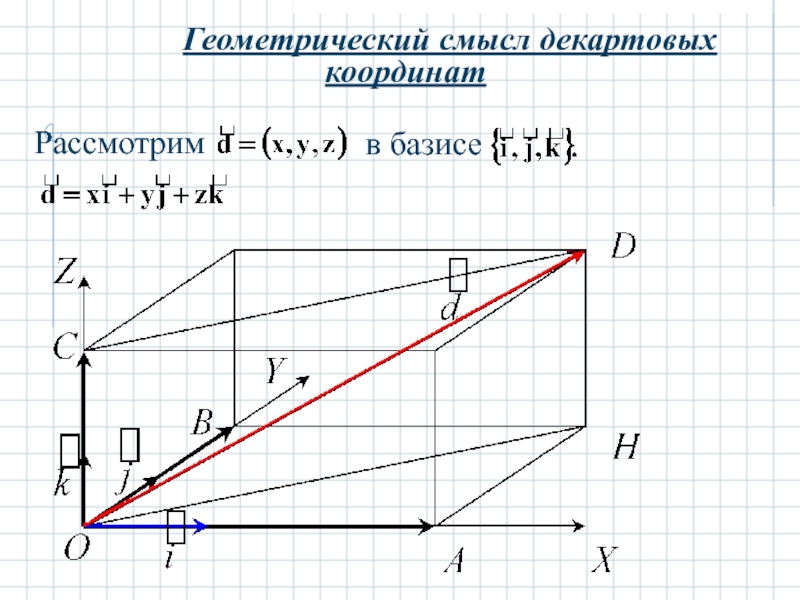
- 19. Геометрический смысл декартовых координат
- 21. Вывод. Декартовы координаты вектора совпадают с
- 22. -основное тождество.
- 23. Вывод. Декартовы координаты вектора
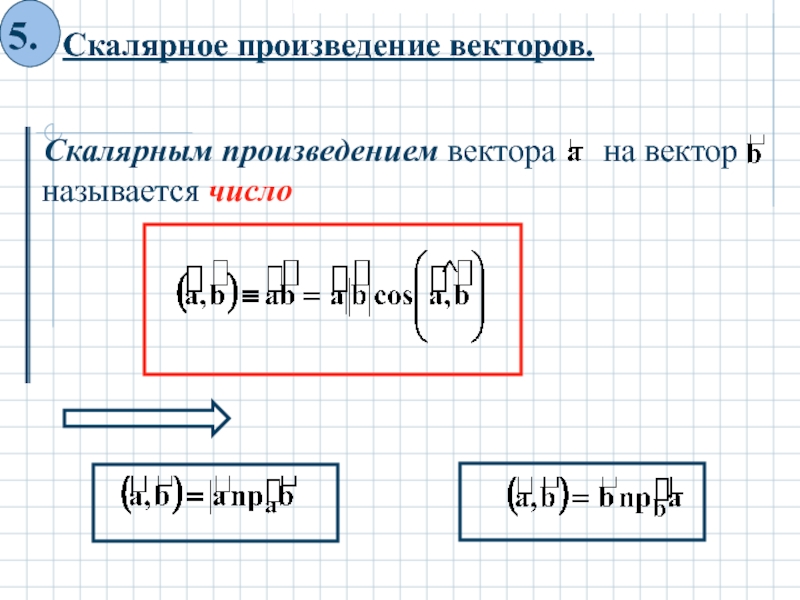
- 24. называется число
- 25. Алгебраические свойства скалярного произведения.
- 26. Геометрические и
- 27. Формула для вычисления скалярного произведения векторов, заданных декартовыми координатами. то
- 28. Тройка векторов называется правой, если кратчайший поворот
- 29. Замечание. Перестановка местами двух соседних
- 31. Обозначение. Пример.
- 32. Алгебраические свойства векторного произведения.
- 33. Геометрические и механические свойства векторного произведения.
- 35. Вычисление векторного произведения в декартовых координатах. то
- 36. называется число
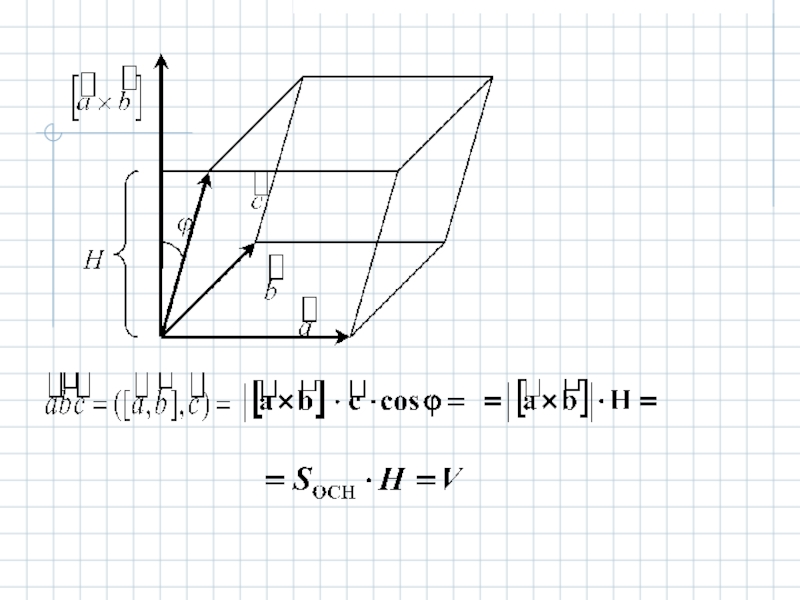
- 37. - объем параллелепипеда …, - тройка векторов компланарна, - тройка левая. Доказательство.
- 39. Следствие. Необходимым и достаточным условием компланарности
- 40. Следствие 1. Необходимым и достаточным
Слайд 2Лекция 4
Векторная алгебра
2. Базис и координаты вектора.
3.
координатной форме.
4. Проекция вектора на ось.
I. Векторы. Линейные операции над векторами.
Линейная зависимость векторов.
5. Скалярное произведение векторов.
6. Векторное произведение векторов.
7. Смешанное произведение векторов.
Слайд 3 Вектор – направленный отрезок;
его
Базовые определения: нулевой вектор,коллинеарные
векторы; компланарные векторы, равные векторы.
Линейные операции над векторами.
I. Сложение векторов
Геометрическое определение –
правило треугольника и правило
параллелограмма:
Слайд 7 Линейная зависимость (ЛЗ) векторов.
Линейной комбинацией (ЛК)
сумма их произведений на произвольные числа:
Если
3.
Слайд 8 Базисом множества векторов на плоскости называются любые два
Базисом множества векторов на прямой называется любой ненулевой вектор этой прямой.
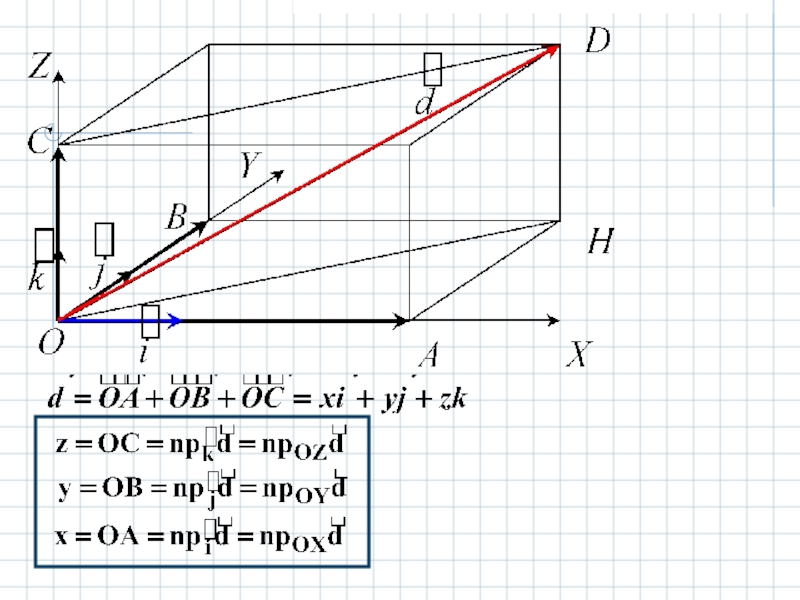
Слайд 21Вывод.
Декартовы координаты вектора совпадают
с его проекциями на соответствующие
координатные оси.
Пусть
Слайд 23 Вывод.
Декартовы координаты вектора позволяют найти его
длину и
Слайд 26 Геометрические и механические свойства скалярного произведения
-длина вектора.
-угол между векторами.
-проекция вектора на вектор.
-работа силы …
Слайд 27Формула для вычисления скалярного произведения
векторов, заданных декартовыми координатами.
то
Слайд 28 Тройка векторов называется правой, если кратчайший поворот от первого вектора ко
Слайд 29 Замечание.
Перестановка местами двух соседних
векторов тройки меняет её ориентацию.
Циклическая перестановка
не меняет её ориентации.
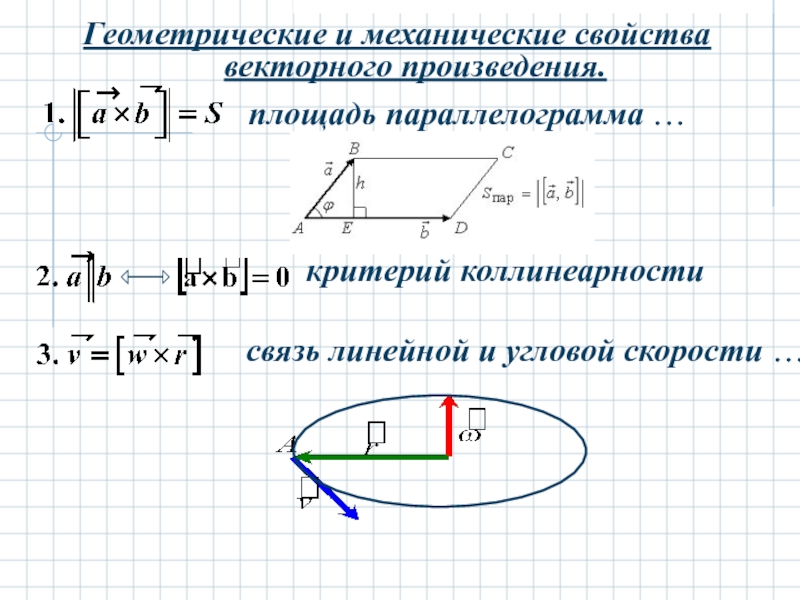
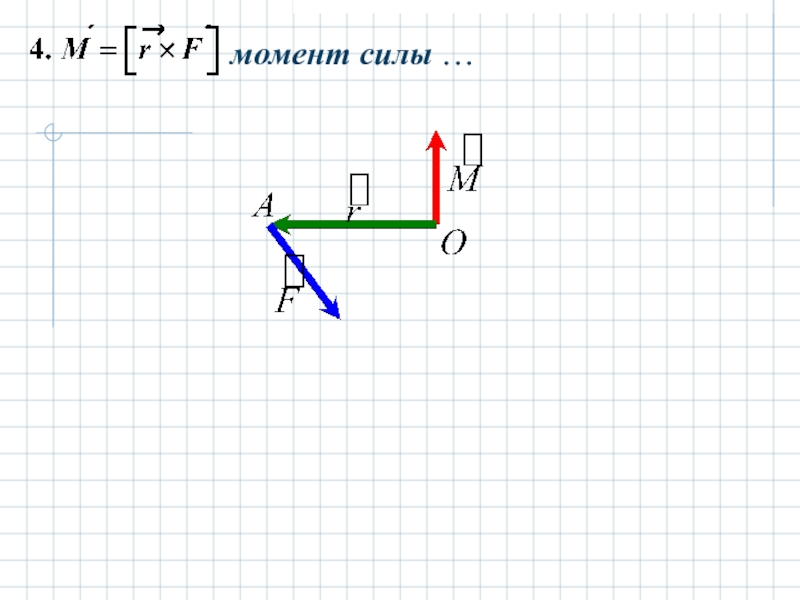
Слайд 33Геометрические и механические свойства векторного произведения.
площадь параллелограмма …
критерий коллинеарности
связь
Слайд 39 Следствие.
Необходимым и достаточным условием компланарности
трёх векторов является равенство нулю их
произведения.
Вычисление смешанного произведения векторов, заданных декартовыми координатами .
то
Слайд 40 Следствие 1.
Необходимым и достаточным условием компланарности
трёх векторов является
строками которого являются координаты этих векторов .
Следствие 2.
Необходимым и достаточным условием линейной
зависимости трёх векторов, является равенство нулю
того же определителя.
Свойство смешанного произведения.
Перестановка местами двух соседних сомножителей
меняет знак смешанного произведения, а циклическая
перестановка сомножителей знака не меняет.