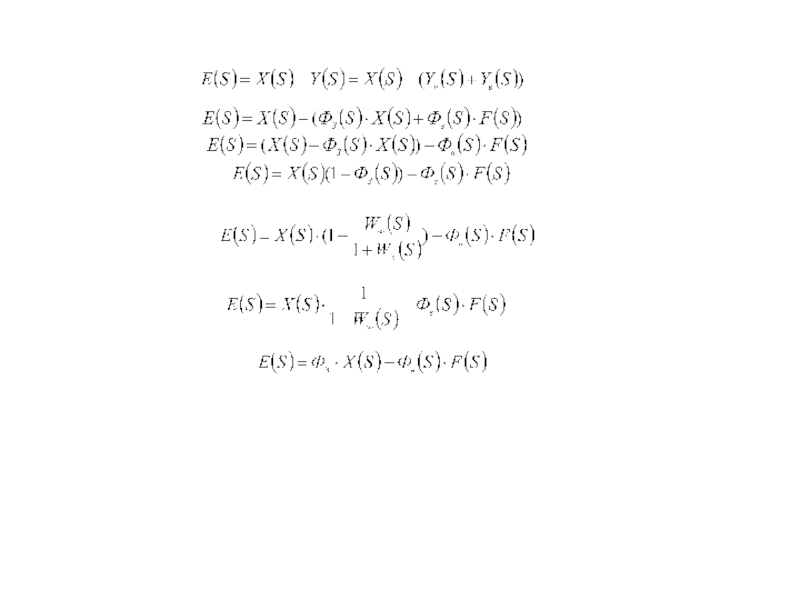- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие управления презентация
Содержание
- 1. Понятие управления
- 2. Понятие управления Управление — это процесс планирования, организации,
- 4. Современный этап развития промышленного производства характеризуется переходом
- 5. Автоматизация – комплекс технических, методических, организационных и
- 6. Процесс развития автоматизации прошел ряд стадий, связанных
- 7. Вторым этапом в развитии автоматизации стала механизация.
- 8. С дальнейшим усложнением производства (высокие температуры, скорости
- 9. 1.1. Системы управления. Системы управления предприятием. Автоматизированные системы управления технологическими процессами.
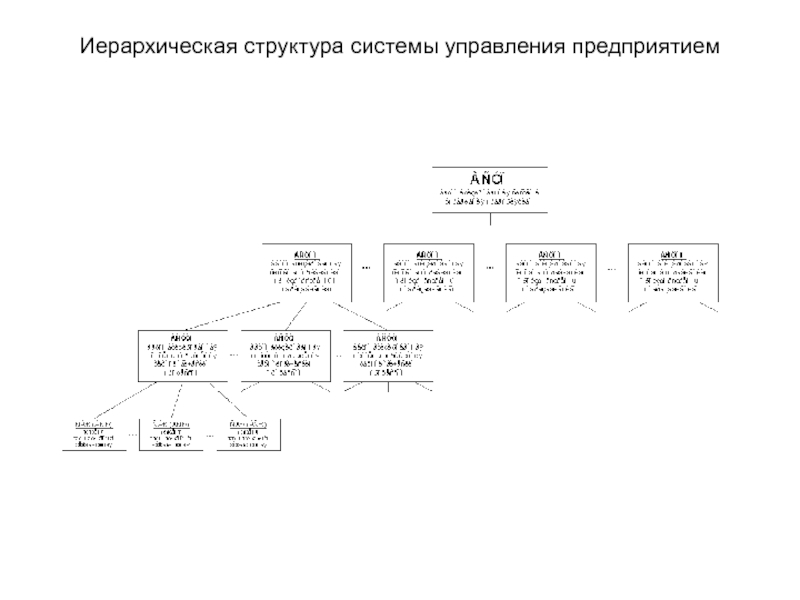
- 10. Укрупненная схема организации производственного предприятия
- 11. Иерархическая структура системы управления предприятием
- 12. Технологический процесс – совокупность технологических операций, проводимых
- 13. 1.2. Основные функции АСУ ТП Основные функции АСУ ТП информационно-измерительная управляющая вспомогательная
- 14. информационно-измерительная: -измерение, отображение и регистрация технологических параметров
- 15. Программно-техническое обеспечение АСУ ТП -технические средства и
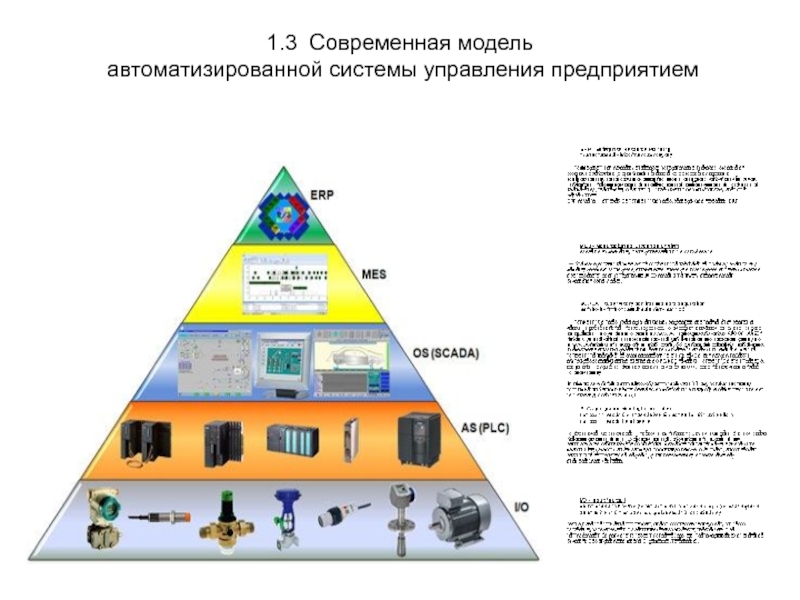
- 16. 1.3 Современная модель автоматизированной системы управления предприятием
- 17. 1.4. Пример представления системы управления (регулирования) технологическим объектом.
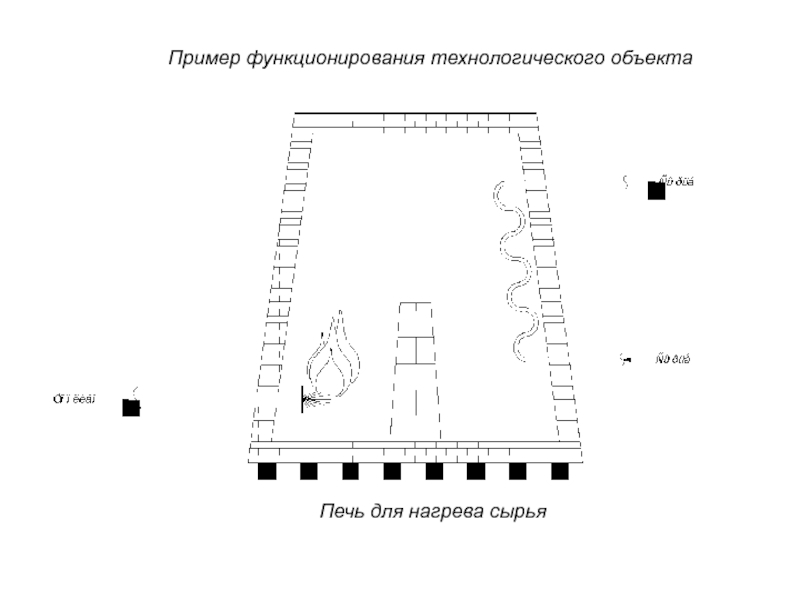
- 18. Пример функционирования технологического объекта Печь для нагрева сырья
- 19. Пример функционирования технологического объекта
- 20. Представление технологического объекта в виде функционального блока
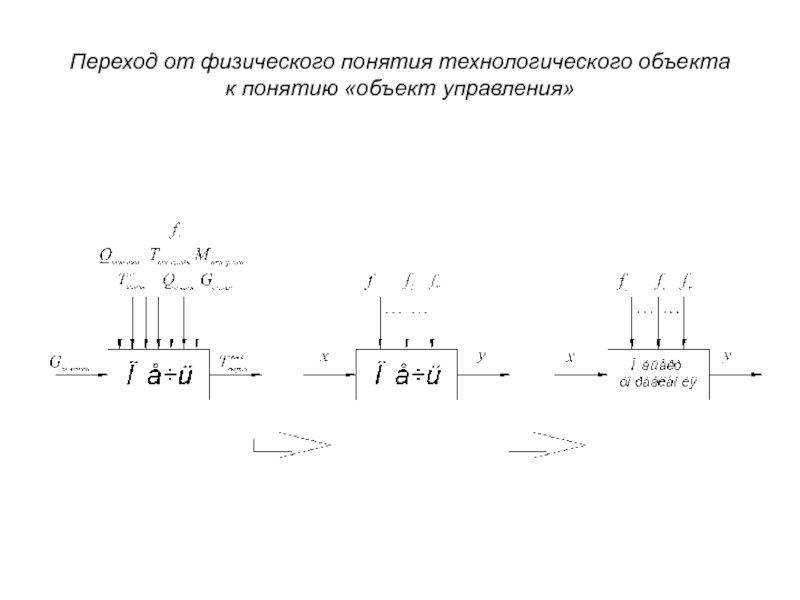
- 21. Переход от физического понятия технологического объекта к понятию «объект управления»
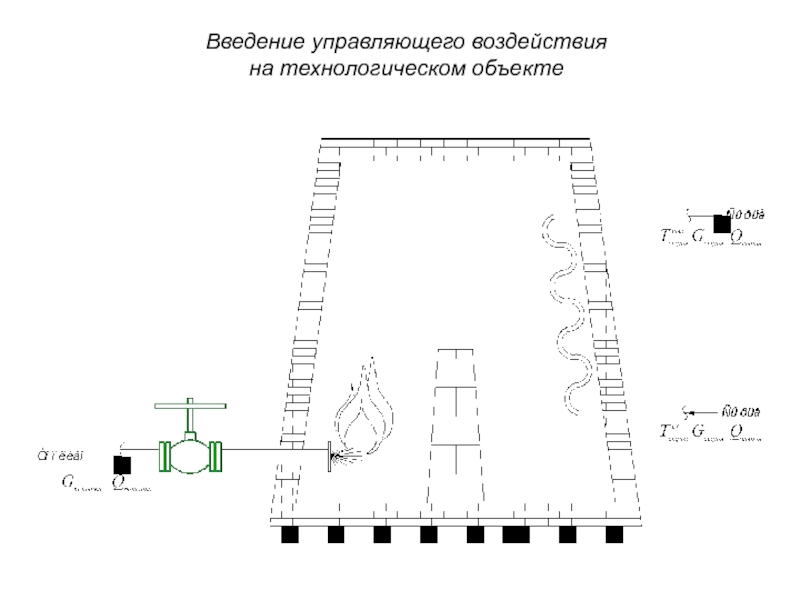
- 22. Введение управляющего воздействия на технологическом объекте
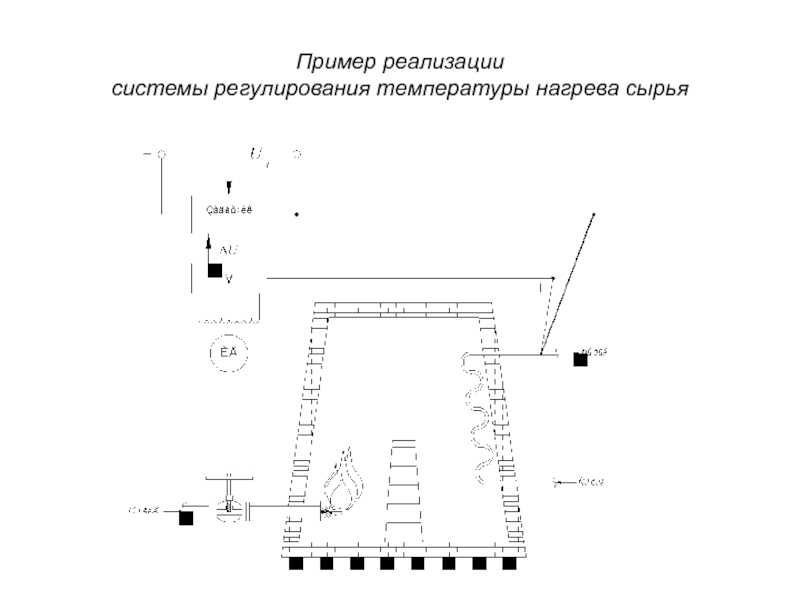
- 23. Пример реализации системы регулирования температуры нагрева сырья
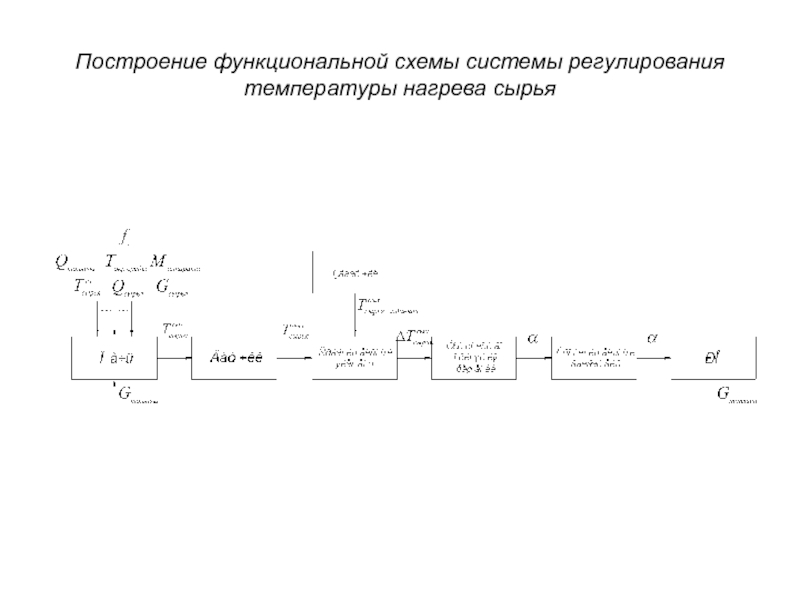
- 24. Построение функциональной схемы системы регулирования температуры нагрева сырья
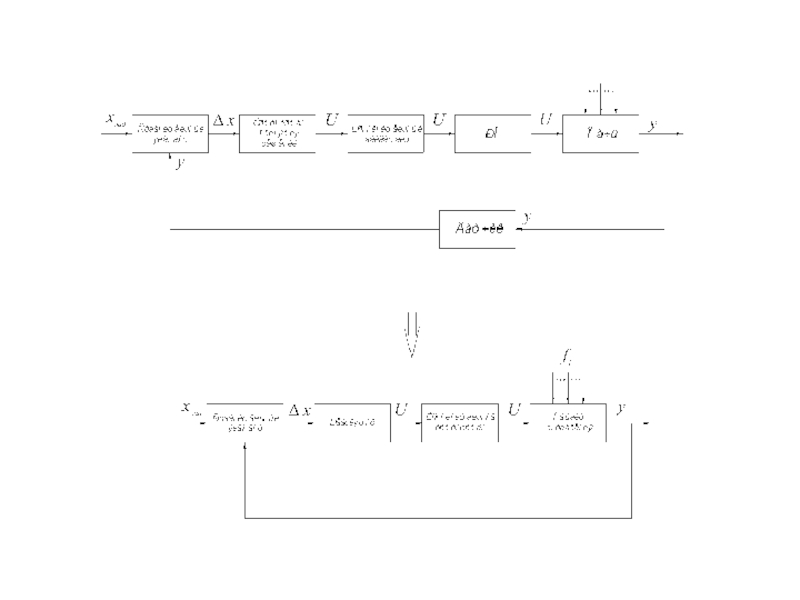
- 25. Преобразование структуры функциональной схемы регулирования
- 27. 2. Основные термины ТАУ
- 28. Объект управления (ОУ) – любой аппарат, машина,
- 29. 2.2.Классификация АСР. Процесс управления возможен при достаточной
- 30. Принцип регулирования по отклонению Достоинства принципа регулирования:
- 31. Принцип регулирования по возмущению Достоинства принципа регулирования:
- 32. Комбинированное регулирование
- 33. 2.2.2. Классификация по виду задающего воздействия По
- 34. 2.2.5. По основным видам уравнений динамики
- 35. 3.Математический аппарат ТАУ
- 36. В теории управления любые физические объекты и
- 37. В ТАУ для упрощения математических моделей применяют
- 39. Теория преобразования Лапласа включает в себя ряд
- 40. Теорема интегрирования при
- 41. 3.2.4. Обратное преобразование Лапласа На практике для
- 42. Тогда, переходя к оригиналу
- 43. С помощью преобразования Лапласа существенно облегчается решение
- 44. 4.Понятие устойчивости в ТАУ
- 45. 4.1. Дифференциальное уравнение. Характеристический полином.
- 46. Решение этого ДУ имеет вид
- 47. Решение однородного дифференциального уравнения или
- 48. 4.2. Понятие устойчивости. Звено или система
- 49. Рассмотрим возможное расположение корней характеристического полинома 4.3. Определение устойчивости по корням характеристического полинома.
- 50. Для каждого из возможных корней рассмотрим соответствующую ему составляющую свободного движения
- 51. Анализ рассмотренных случаев расположения корней характеристического полинома
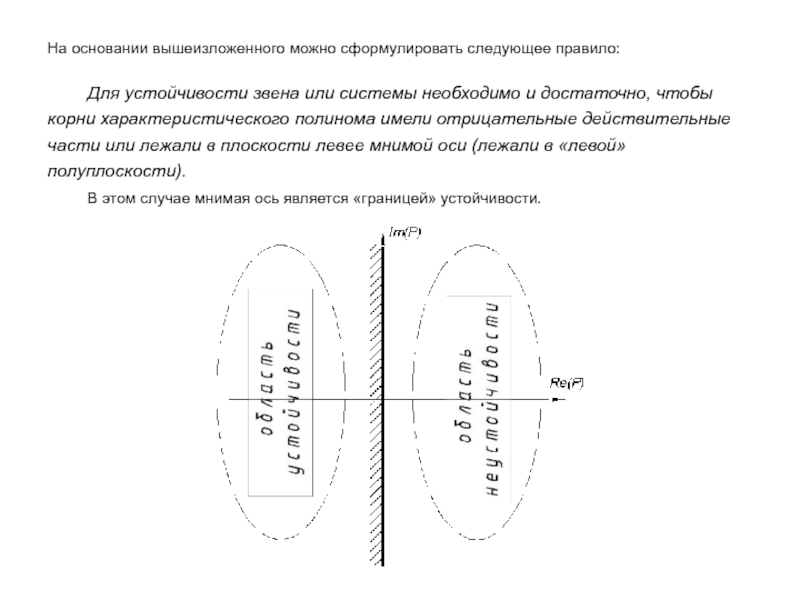
- 52. На основании вышеизложенного можно сформулировать следующее правило:
- 53. 5. Понятие передаточной функции
- 54. Рассмотрим некоторый объект (звено) описываемый дифференциальным уравнением
- 55. Свойства передаточной функции. Передаточная функция является полным
- 56. Так же передаточная функция является инструментом для определения динамических характеристик звеньев и систем.
- 57. 6. Динамические характеристики
- 58. Для оценки динамических свойств объектов, устройств, систем
- 59. 6.1. Временные характеристики. 6.1.1. Импульсная (весовая) характеристика.
- 60. Переходной характеристикой называется
- 61. 6.2. Частотные характеристики. Частотными характеристиками называются формулы
- 62. Выражение носит название комплексной
- 63. Графически АФЧХ изображается на комплексной плоскости в
- 64. Связь частотных характеристик с декартовыми координатами:
- 66. 8. Эквивалентные преобразования соединения звеньев
- 67. Сложное соединение простых звеньев может быть преобразовано
- 68. 8.1 Последовательное соединение звеньев.
- 69. 8.2 Параллельное соединение звеньев.
- 70. 8.3 Соединение с местной обратной связью.
- 71. 9. Характеристики замкнутой линейной АСР
- 72. Вычисление характеристик одноконтурной системы. Замкнутая система является
- 73. В этой системе два входных сигнала
- 74. Определим реакцию АСР на входной сигнал возмущения.
- 75. Кроме этих двух основных передаточных функций замкнутой
Слайд 2Понятие управления
Управление — это процесс планирования, организации, мотивации и контроля, необходимый для
Управление — в теории: наука о принципах и методах управления различными системами.
Управление технической системой – создание условий, обеспечивающих требуемое протекание технологического процесса, то есть поддержание необходимого технологического режима с точки зрения качества получаемой продукции.
Слайд 4 Современный этап развития промышленного производства характеризуется переходом к высоким технологиям, стремлением
Слайд 5Автоматизация – комплекс технических, методических, организационных и других мероприятий, позволяющих вести
Слайд 6 Процесс развития автоматизации прошел ряд стадий, связанных с соответствующим уровнем развития
Первым этапом автоматизации явилось ручное управление.
Человек первоначально решал сам все задачи и приводил в исполнение свои решения. Вручную открывал/закрывал задвижки изменяя потоки/количества вещества или энергии, оценивал состояние процессов/аппаратов «на глаз».
Человек и принимает решения и приводит их в исполнение
Слайд 7 Вторым этапом в развитии автоматизации стала механизация. Производство усложнялось, требовалось более
В механизированном производстве человек принимает непосредственное участие в процессе управления, но освобожден от тяжелого физического труда. Основная его задача – принятие решений.
Механизация облегчает труд, уменьшает численность персонала, увеличивает производительность труда.
В механизированном производстве человек принимает непосредственное участие в процессе управления, но освобожден от тяжелого физического труда. Основная его задача – принятие решений.
Механизация облегчает труд, уменьшает численность персонала, увеличивает производительность труда.
Слайд 8 С дальнейшим усложнением производства (высокие температуры, скорости реакций и пр.) человек
Современный этап развития автоматизации характеризуется широким применением вычислительной техники для управления производством. Однако, любая система управления предполагает участие человека в процессе управления.
Слайд 91.1. Системы управления.
Системы управления предприятием.
Автоматизированные системы управления технологическими процессами.
Слайд 12 Технологический процесс – совокупность технологических операций, проводимых над исходным сырьем в
Технологический объект – совокупность технологического оборудования и реализованного на нем по соответствующему регламенту технологического процесса производства. Технологический объект является составной частью технологического процесса.
Задача управления технологическим процессом состоит в выработке оптимальных режимных параметров технологических аппаратов и оборудования для обеспечение желаемого протекания процесса, качества и количества продукции.
Задача управления технологическим объектом – поддержание заданных режимных параметров (давление, температура, уровень, концентрация и пр.).
Слайд 131.2. Основные функции АСУ ТП
Основные функции АСУ ТП
информационно-измерительная
управляющая
вспомогательная
Слайд 14информационно-измерительная:
-измерение, отображение и регистрация технологических параметров и состояния оборудования;
-косвенные измерения;
-обнаружение отклонений;
-регистрация
-прогноз протекания технологического процесса.
управляющая:
-поддержание заданных технологических параметров в условиях действующих возмущений;
-изменение параметров по определенному закону;
-распределение нагрузки между аппаратами;
-управление в режимах пуска-останова;
-управление в нестандартных условиях (аварийная защита и блокировка).
вспомогательная:
-архивирование событий;
-обмен информацией с системами высших уровней иерархии.
Слайд 15Программно-техническое обеспечение АСУ ТП
-технические средства и обеспечение (датчики, преобразователи, усилители, системы
-программное обеспечение (общесистемное и специальное программное обеспечение).
Слайд 28Объект управления (ОУ) – любой аппарат, машина, агрегат в котором протекает
Регулируемая величина – физический параметр, характеризующий состояние объекта управления (ОУ).
Задание (задающие воздействие) - желаемое значение регулируемой величины.
Ошибка регулирования - отклонение регулируемой величины от заданного значения.
Возмущающее воздействие (возмущение) - внешнее воздействие стремящееся вызвать нежелательное отклонение регулируемой величины от заданного значения.
Управляющее воздействие - воздействие наносимое системой регулирования на объект с целью выведения регулируемой величины на заданное значение.
Регулятор – совокупность автоматически действующих устройств, обеспечивающих процесс регулирования без участия человека.
Автоматическое регулирование – поддержание постоянным значения некоторой физической величины, или изменение ее по некоторому, возможно заранее неизвестному закону, с помощью автоматически действующих устройств.
2.1. Основные понятия и определения ТАУ
Слайд 292.2.Классификация АСР.
Процесс управления возможен при достаточной информации:
- о цели управления;
- о
- о характеристиках объекта;
- о возмущениях среды.
В зависимости от характера и полноты доступной информации реализуют различные принципы регулирования
- принцип регулирования по отклонению;
- принцип регулирования по возмущению;
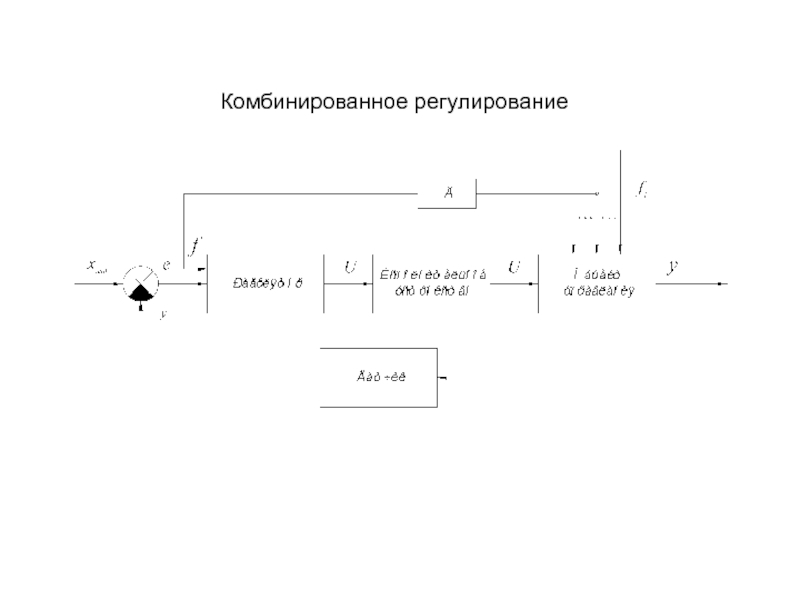
- комбинированное регулирование.
2.2.1.Классификация по принципу регулирования
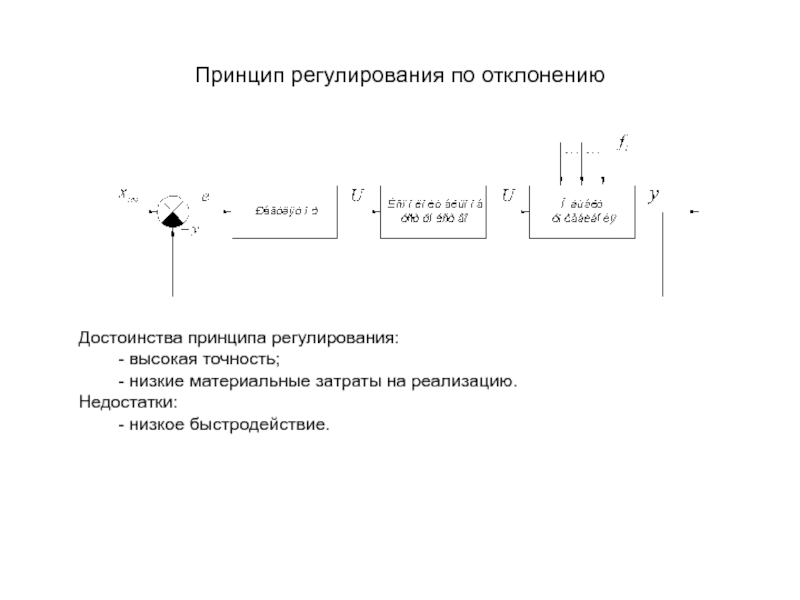
Слайд 30Принцип регулирования по отклонению
Достоинства принципа регулирования:
- высокая точность;
- низкие материальные затраты
Недостатки:
- низкое быстродействие.
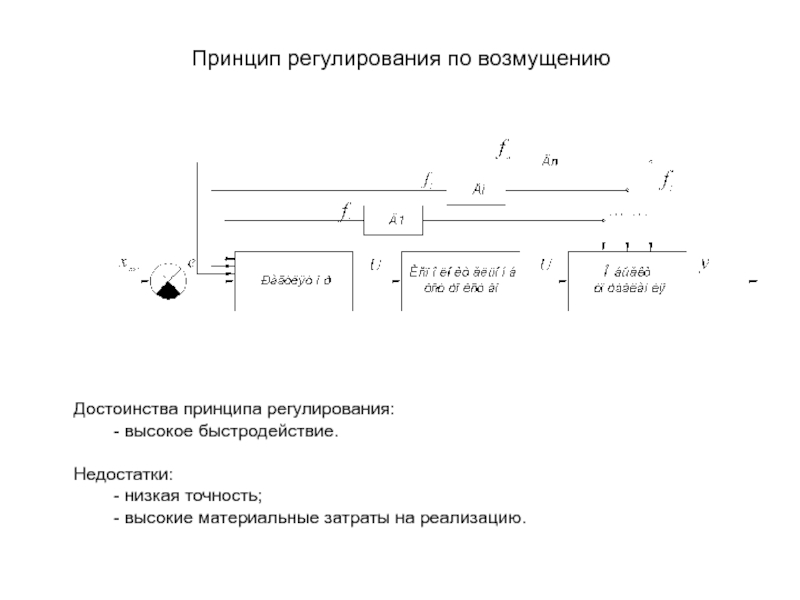
Слайд 31Принцип регулирования по возмущению
Достоинства принципа регулирования:
- высокое быстродействие.
Недостатки:
- низкая точность;
- высокие
Слайд 332.2.2. Классификация по виду задающего воздействия
По виду задающего воздействия
- системы стабилизации ;
- системы программного управления;
- следящие системы.
2.2.4. Многосвязные и односвязные АСР
По типу используемых сигналов АСР делят на:
- непрерывные АСР ;
- дискретные АСР.
2.2.3. Классификация по типу используемых сигналов
Односвязные АСР – каждой регулируемой величине соответствует свой регулирующий орган и управляющее воздействие.
Многосвязные АСР – изменение одного управляющего воздействия приведет к изменению нескольких регулируемых величин.
Слайд 36В теории управления любые физические объекты и явления рассматриваются в виде
Математическая модель – совокупность уравнений, позволяющих определить (рассчитать) выходной сигнал по известному входному сигналу.
Основой для анализа и синтеза АСР является математическая модель как АСР в целом, так и отдельных ее звеньев.
Наиболее широко употребляемой является математическая модель в виде дифференциального уравнения
3.1. Математические модели в АСР.
Слайд 37В ТАУ для упрощения математических моделей применяют аппарат операционного исчисления –
Операционное исчисление – совокупность методов прикладного математического анализа, позволяющих экономно и непосредственно ведущими к цели средствами получать решения линейных дифференциальных уравнений.
Однако эти модели подразумевают операции интегрирования и дифференцирования, что значительно усложняет анализ и синтез систем в смысле расчетов.
3.2. Преобразование Лапласа
3.2.1. Прямое преобразование Лапласа
При преобразовании Лапласа функции действительного переменного (функция-оригинал) ставится в соответствие функция комплексного переменного (функция-изображение).
Слайд 38
Во многих случаях при нахождении решения можно избежать вычисления
3.2.2. Таблица простейших оригиналов и их изображений
Слайд 39Теория преобразования Лапласа включает в себя ряд теорем (свойств), опираясь на
Теорема линейности.
Теорема дифференцирования
при нулевых начальных условиях
3.2.3. Свойства преобразования Лапласа
Слайд 40Теорема интегрирования
при нулевых начальных условиях
Теорема запаздывания (смещения)
Теорема о начальных и конечных
Слайд 413.2.4. Обратное преобразование Лапласа
На практике для нахождения оригинала по известному изображению
Пусть является рациональной функцией:
Из курса математики сложную дробь можно разложить на сумму простых дробей
Переход от изображения к оригиналу осуществляется по формуле обратного преобразования Лапласа.
Слайд 42Тогда, переходя к оригиналу
Из таблицы оригиналов и изображений:
Можно записать
Таким образом, можно
Слайд 43С помощью преобразования Лапласа существенно облегчается решение ДУ:
1.Для заданного ДУ и
2.Решают уравнение в изображениях и переходят к оригиналу (обратное преобразование Лапласа).
3.2.5.* Решение дифференциальных уравнений с помощью теории преобразования Лапласа
Слайд 454.1. Дифференциальное уравнение.
Характеристический полином.
В дальнейшем будем понимать исходным математическим
Или
Если ввести оператор дифференцирования
исходное ДУ примет вид
обозначим
Слайд 46Решение этого ДУ имеет вид
где - свободная
или
Это однородное уравнение описывает свободное (автономное) движение системы при отсутствии внешних воздействий.
Составляющая - вынужденная составляющая (установившийся процесс), определяется внешними воздействиями и является частным решением неоднородного дифференциального уравнения.
Слайд 47Решение однородного дифференциального уравнения
или
определяется как
Тогда решение исходного дифференциального уравнения можно представить
На основании этого можно сделать вывод, что свободное движение в системе (или звене) может быть представлено в виде суммы экспонент и зависит от показателей степени – корней полинома
Поэтому, полином называют характеристическим полиномом. Так как он «характеризует» (дает описание) собственные внутренние свойства системы или отдельного звена.
Слайд 484.2. Понятие устойчивости.
Звено или система называются устойчивыми если свободная составляющая
с ростом
Звено или система называются неустойчивыми если свободная составляющая с ростом времени неограниченно растет.
Звено или система находятся на границе устойчивости если предел свободной составляющей с ростом времени равен константе или не существует.
Слайд 49Рассмотрим возможное расположение корней характеристического полинома
4.3. Определение устойчивости
по корням характеристического полинома.
Слайд 50Для каждого из возможных корней рассмотрим соответствующую ему составляющую свободного движения
Слайд 51 Анализ рассмотренных случаев расположения корней характеристического полинома и соответствующих ему
если - свободное движение или переходная составляющая устойчива;
если - свободное движение или переходная составляющая неустойчива;
если - свободное движение или переходная составляющая находится на границе устойчивости
Слайд 52На основании вышеизложенного можно сформулировать следующее правило:
Для устойчивости звена или системы
В этом случае мнимая ось является «границей» устойчивости.
Слайд 54Рассмотрим некоторый объект (звено) описываемый дифференциальным уравнением общего вида.
Преобразуя это уравнение
Исходя из этого выражения можно определить изображение выходной величины
Передаточная функция – это отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.
Слайд 55Свойства передаточной функции.
Передаточная функция является полным аналогом дифференциального уравнения в области
Знаменатель передаточной функции есть характеристический полином.
Для звена или системы с несколькими входами передаточная функция определяется по каждому входному воздействию в отдельности.
Слайд 56 Так же передаточная функция является инструментом для определения динамических характеристик звеньев
Слайд 58 Для оценки динамических свойств объектов, устройств, систем в целом широко используют
Динамическая характеристика – реакция звена или системы на некоторое стандартное или типовое входное воздействие.
По экспериментально полученным динамическим характеристикам можно определить с достаточной степенью точности передаточную функцию.
Динамические характеристики делят на временные и частотные.
Слайд 596.1. Временные характеристики.
6.1.1. Импульсная (весовая) характеристика.
Импульсной (импульсной переходной) характеристикой
Импульсная характеристика может быть найдена с помощью обратного преобразования Лапласа:
Тогда, изображение выходного сигнала есть сама передаточная функция, а импульсная характеристика является оригиналом передаточной функции.
Слайд 60 Переходной характеристикой называется реакция звена (или системы)
Переходная характеристика может быть найдена с помощью обратного преобразования Лапласа:
Если сравнить между собой изображение импульсной характеристики и переходной
можно сказать: для того чтобы получить изображение импульсной характеристик, нужно изображение переходной умножить на . В области оригиналов умножение на соответствует операции дифференцирования. Можно сделать вывод , что импульсная характеристика есть дифференциал переходной.
6.1.2. Переходная характеристика.
Слайд 616.2. Частотные характеристики.
Частотными характеристиками называются формулы и графики, характеризующие реакцию звена
С помощью преобразования Фурье можно показать, что реакция линейного звена или системы на синусоиду есть так же синусоида той же частоты, что и входные колебания.
Установившаяся выходная синусоида отлична от входных колебаний по амплитуде и имеет фазовый сдвиг.
Эти изменения амплитуды и фазы выходной синусоиды относительно входной в зависимости от частоты (входной синусоиды) и описывают частотные характеристики.
Слайд 62 Выражение
носит название комплексной частотной характеристики или частотной передаточной функции
Комплексная частотная характеристика может быть получена путем подстановки в передаточную функцию .
Слайд 63 Графически АФЧХ изображается на комплексной плоскости в координатах
Формально, АФЧХ есть вектор на комплексной плоскости с длиной и углом поворота относительно действительной положительной полуоси.
С изменением частоты конец вектора описывает некоторую кривую, которую и называют АФЧХ.
Амплитудно-частотная характеристика – это модуль .
Представляет собой зависимость отношения амплитуды входной синусоиды к амплитуде входной от частоты.
Фазово-частотная характеристика - это аргумент .
Представляет собой зависимость фазового сдвига между синусоидами от входной частоты.
Слайд 67 Сложное соединение простых звеньев может быть преобразовано в более простые соединения
Предполагаем, что звенья являются направленными и их передаточные функции независимы от их соединения.
Рассмотрим три вида соединения звеньев:
-последовательное;
-параллельное (параллельное согласное);
-с местной обратной связью (параллельное встречное).
Слайд 72Вычисление характеристик одноконтурной системы.
Замкнутая система является одноконтурной, если при ее размыкании
Часто многоконтурную АСР можно привести к одноконтурной с помощью перестановки и переноса узлов и сумматоров, эквивалентных преобразований.
Рассмотрим одноконтурную систему, сводящуюся к следующей структуре
Слайд 73В этой системе два входных сигнала -
Определим реакцию АСР на входной сигнал задания.
Выражение называется передаточной функцией замкнутой системы по заданию