- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
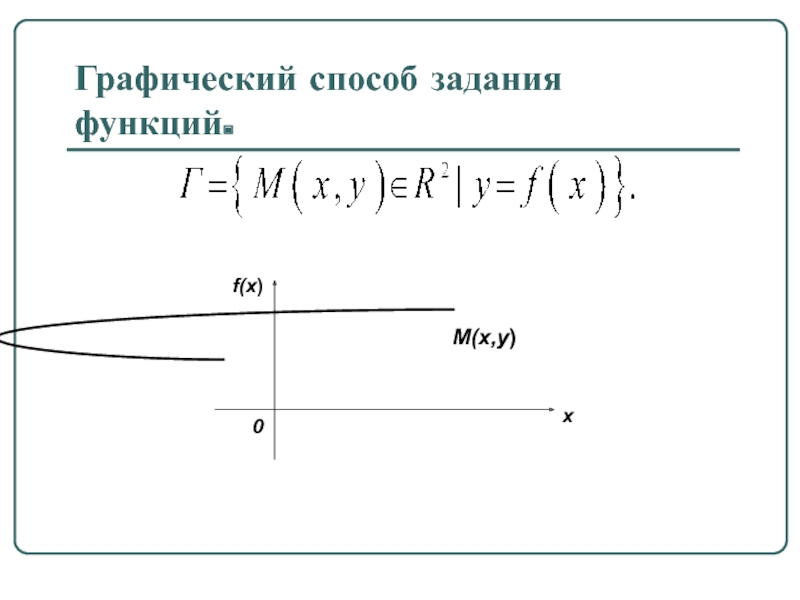
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие множества. Логические символы презентация
Содержание
- 1. Понятие множества. Логические символы
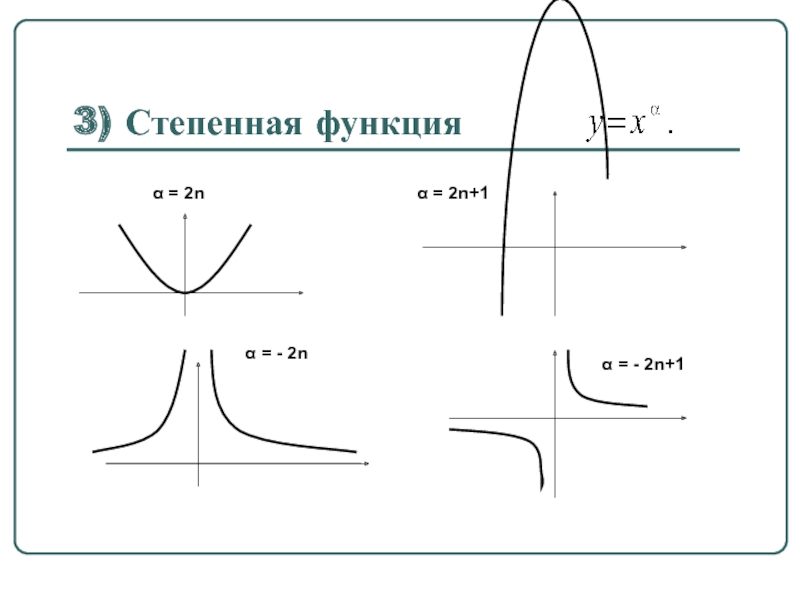
- 2. 1. МНОЖЕСТВА 1.1. ПОНЯТИЕ МНОЖЕСТВА. ЛОГИЧЕСКИЕ СИМВОЛЫ.
- 3. Логические символы. ∈- знак принадлежности ∀-
- 4. Множества. Способы задания. {a} -
- 5. Отношения между множествами. Определение 1.1. Множества A
- 6. Пример:
- 7. Свойства равенства: A=A
- 8. Определение 1.2. Множество A (A ≠
- 9. 1.2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ. V – основное
- 10. Диаграмма Эйлера-Венна.
- 11. Свойства объединения множеств. 1) A ⎩⎭ B
- 12. Определение 1.4. Пересечением множеств A и B
- 13. Диаграмма Эйлера-Венна.
- 14. Свойства пересечения множеств. 1) A ⎧⎫ B
- 15. Определение 1.5. Разностью двух множеств B и
- 16. Диаграмма Эйлера-Венна.
- 17. Определение 1.6. Разность V \ A называется
- 18. Диаграмма Эйлера-Венна:
- 19. Пара элементов ( x ; y
- 20. Определение 1.7. Декартовым произведением двух множеств A
- 21. y
- 22. 1.3. ОТОБРАЖЕНИЕ МНОЖЕСТВ. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ. Пусть A
- 23. Определение отображения: f : A → B
- 24. Определение 1.8. Отображение f : A →
- 25. ЛЕКЦИЯ 2 2. ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ.
- 26. f – взаимно однозначное отображение ⇔
- 27. Пример:
- 28. Определение 1.10. Два множества A и B
- 29. 1.4. ЧИСЛОВЫЕ МНОЖЕСТВА. Множество натуральных чисел N.
- 30. Множество целых чисел Z. Z = {
- 31. Множество рациональных чисел Q. Q = {
- 32. Множество действительных чисел R. Свойства: R
- 33. 2.1 ПОНЯТИЕ ФУНКЦИИ. СПОСОБЫ ЗАДАНИЯ. Пусть D
- 34. Термины функция, отображение, преобразование – синонимы.
- 35. Аналитический способ задания функций. С помощью формул
- 36. Пример:
- 37. Составные функции:
- 38. Неявно заданные функции: F(x,y)=0 Если уравнение можно
- 39. Табличный способ задания функций.
- 40. Графический способ задания функций.
- 41. Не является графиком функции:
- 42. 2.2 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОВЕДЕНИЯ
- 43. 4) Монотонность: монотонно возрастающая, если
- 44. 2.3 СЛОЖНАЯ ФУНКЦИЯ. ОБРАТНАЯ ФУНКЦИЯ. Сложная функция.
- 45. Обратная функция. Функция y=f(x) отображает D(f) →
- 46. Теорема 2.1. Если числовая функция монотонна, то
- 47. Построение графика обратной функции.
- 48. 2.4. ОСНОВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ И ИХ ГРАФИКИ.
- 49. 2) Квадратичная функция.
- 50. 3) Степенная функция
- 51. 4) Показательная функция.
- 52. 5) Логарифмическая функция
- 53. y = ch x 6) Тригонометрические
- 54. ЛЕКЦИЯ 3 2. ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ.
- 55. 2.5. КЛАССИФИКАЦИЯ ФУНКЦИЙ. 1) Целые рациональные функции:
- 56. 2.6. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ. t
- 57. Пример: а) Введем Тогда
- 58. Параметрическое задание линий на плоскости. Множество точек
- 59. Окружность с центром в начале координат.
- 60. Парабола. Гипербола.
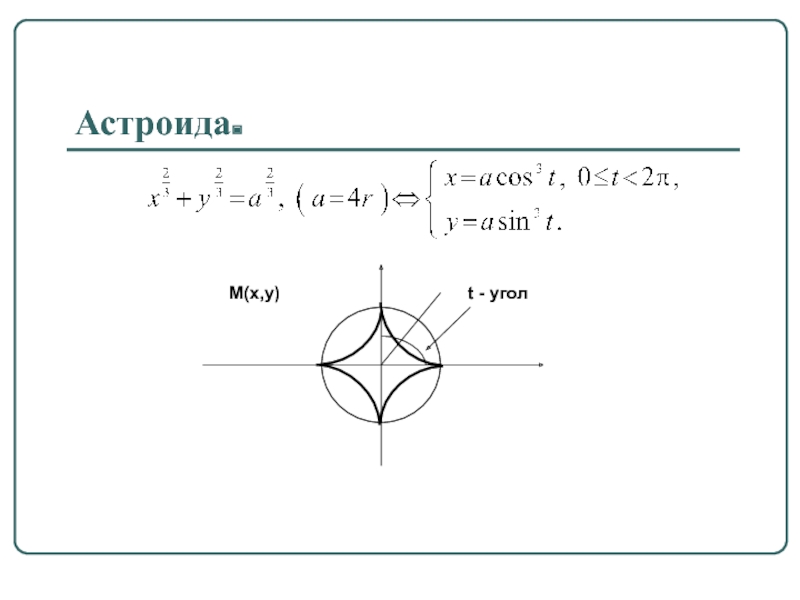
- 61. Астроида.
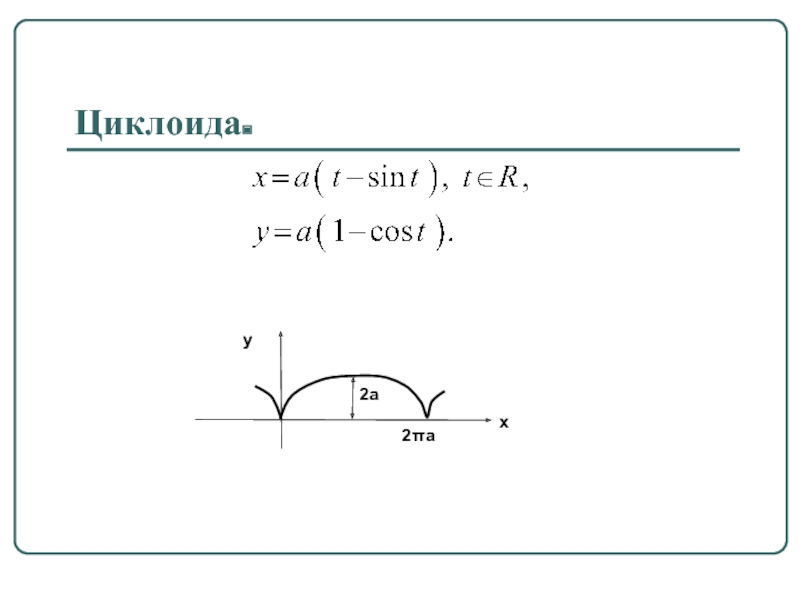
- 62. Циклоида.
Слайд 1МАТЕМАТИЧЕСКИЙ АНАЛИЗ 1
Лектор: Бутырин Владимир Иванович
К.т.н., доцент.
Телефон кафедры 346-07-33.
Корпус 1, ком.
Слайд 3Логические символы.
∈- знак принадлежности
∀- квантор всеобщности
∃- квантор существования
⇒-
⇔- символ эквивалентности
Слайд 4Множества. Способы задания.
{a} - одноэлементное множество;
∅- пустое множество
Действительные корни уравнения
∃
Если A - конечное множество, то число его элементов ⏐A⏐ - мощность множества.
Слайд 5Отношения между множествами.
Определение 1.1. Множества A и B называются равными, если
Обозначают A=B.
Слайд 7Свойства равенства:
A=A
A=B, B=C ⇒ A=C (транзитивность);
A=B ⇒ B=A (симметричность).
Неравенство множеств обозначают
A ≠ B.
Слайд 8Определение 1.2.
Множество A (A ≠ ∅) называется подмножеством множества B
Обозначение: A ⊆ B ⇔ ∀ a ∈ A ⇒ a ∈ B.
Если A ⊆ B и A ≠ B ⇒ A ⊂ B.
Пример: N ⊂ Z ⊂ Q ⊂ R.
Слайд 91.2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.
V – основное или универсальное множество.
1) В планиметрии
2) Для функций действительной переменной V = R.
Определение 1.3. Объединением множеств A и B называется множество A ⎩⎭ B, содержащее те и только те элементы, которые принадлежат хотя бы одному из множеств A или B (или обоим одновременно).
Пример: A = {2,3,4,6}, B = {1,2,3,4,5,6} ⇒ A⎩⎭B = {1,2,3,4,5,6}.
Слайд 11Свойства объединения множеств.
1) A ⎩⎭ B = B ⎩⎭ A
2) A ⎩⎭ ( B ⎩⎭ C ) = ( A ⎩⎭ B ) ⎩⎭ C (ассоциативность).
Очевидно
A ⎩⎭ A = A, A ⎩⎭ ∅ =A, A ⎩⎭ V = V.
Слайд 12Определение 1.4.
Пересечением множеств A и B называется множество A ⎧⎫ B,
A ⎧⎫ B = { x ⏐ x ∈ A ∧ x ∈ B }.
Слайд 14Свойства пересечения множеств.
1) A ⎧⎫ B = B ⎧⎫ A
2) A ⎧⎫ ( B ⎧⎫ C ) = ( A ⎧⎫ B ) ⎧⎫ C (ассоциативность).
Очевидно, что
A ⎧⎫ A = A, A ⎧⎫ ∅ = ∅, A ⎧⎫ V = A.
Операции объединения и пересечения подчиняются дистрибутивным законам:
A ⎧⎫ ( B ⎩⎭ C ) = ( A ⎧⎫ B ) ⎩⎭ ( A ⎧⎫ C ),
A ⎩⎭ ( B ⎧⎫ C ) = ( A ⎩⎭ B ) ⎧⎫ ( A ⎩⎭ C ).
Слайд 15Определение 1.5.
Разностью двух множеств B и A называется множество B \
B \ A = { x ⏐ x ∈ B ∧ x ∉ A }.
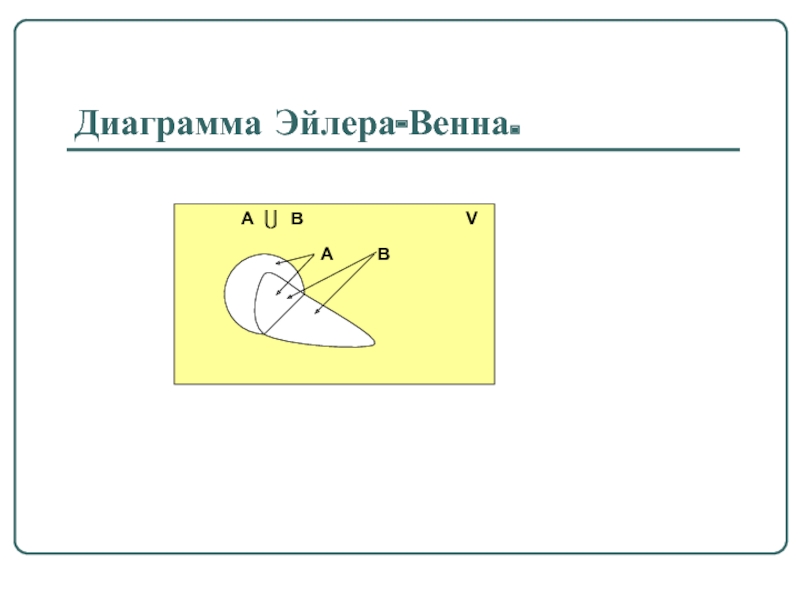
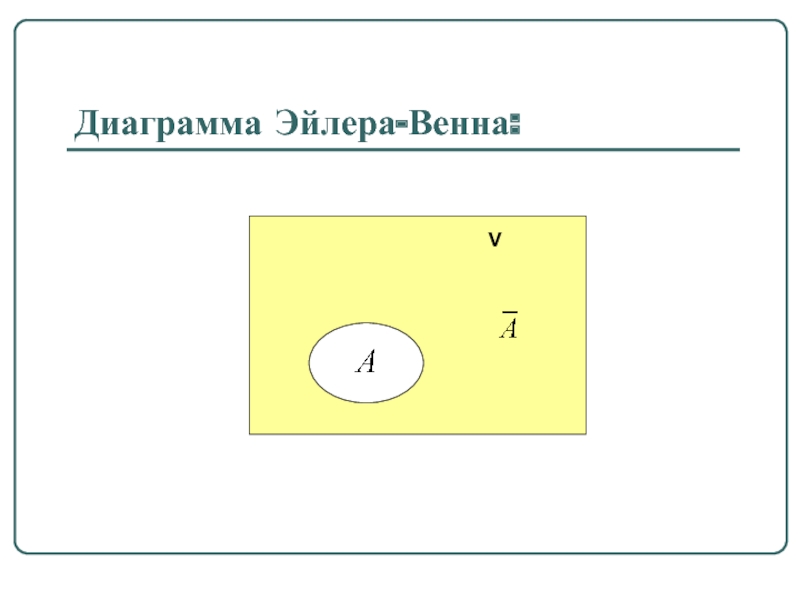
Слайд 17Определение 1.6.
Разность V \ A называется дополнением множества A до универсального
Примеры:
Слайд 19
Пара элементов ( x ; y ), x ∈ A, y
Считается, что
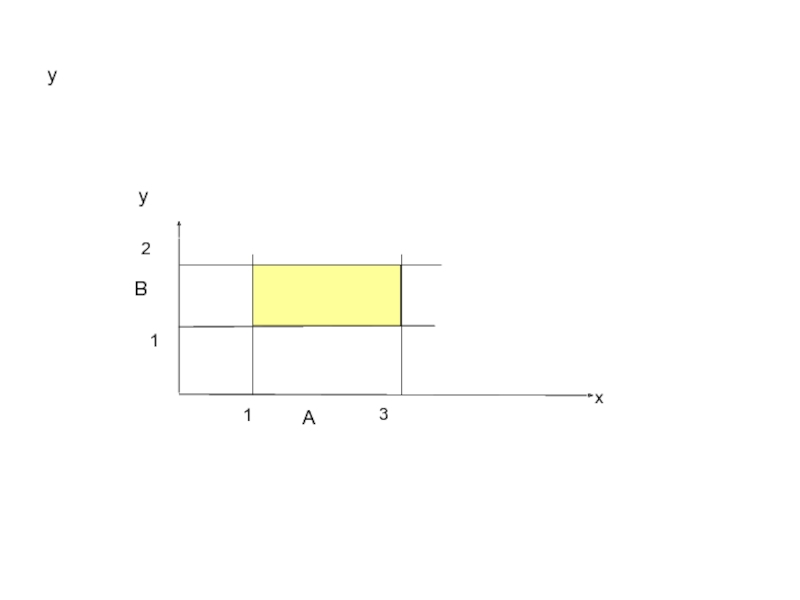
Слайд 20Определение 1.7.
Декартовым произведением двух множеств A и B называется множество, обозначаемое
A × B = { ( x ; y ) | ∀ x ∈ A , ∀ y ∈ B }.
Слайд 221.3. ОТОБРАЖЕНИЕ МНОЖЕСТВ. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ.
Пусть A и B - произвольные множества.
Пусть
Говорят, что задано отображение f A в B или оператор f A в B.
Обозначение: f : A → B или
b – образ элемента a (обозначают f(a) );
a – прообраз элемента b = f(a).
Слайд 23Определение отображения:
f : A → B ⇔ ∀ a ∈ A
Множество образов всех элементов a ∈ A при отображении f называют образом множества A при этом отображении и обозначают:
f(a)={ f(a) | a∈A } ⊂ B.
Задание отображения – это задание тройки ( A, f, B ).
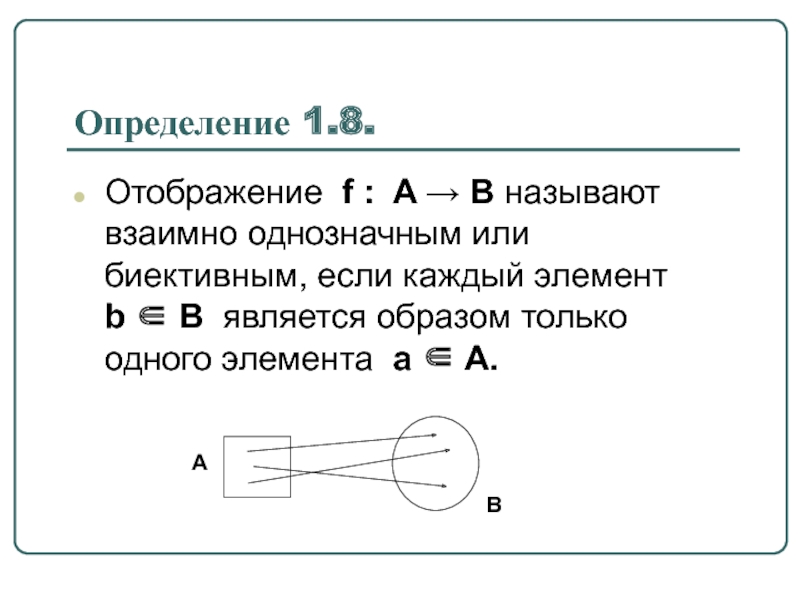
Слайд 24Определение 1.8.
Отображение f : A → B называют взаимно однозначным или
Слайд 26
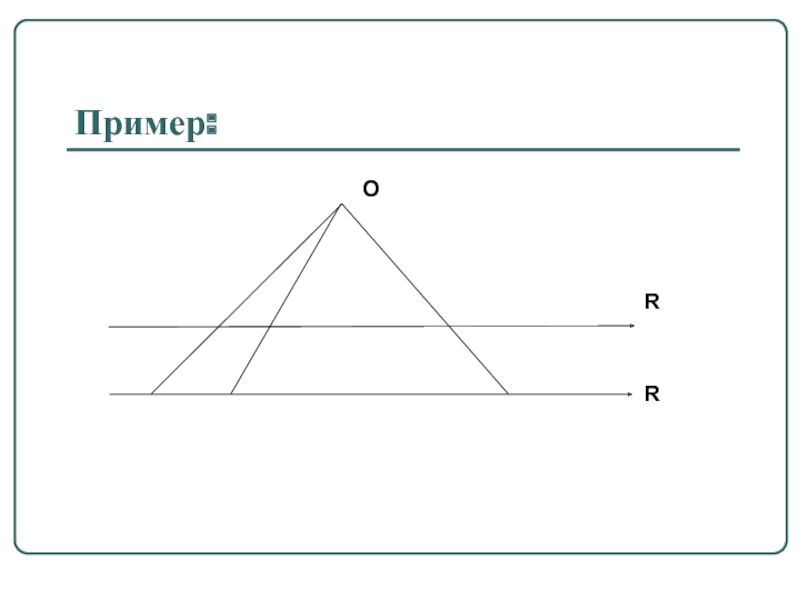
f – взаимно однозначное отображение ⇔ ∀ b ∈ B ∃
Если f - взаимно однозначное отображение, то можно говорить об обратном отображении.
Слайд 28Определение 1.10.
Два множества A и B называются эквивалентными (равномощными), если ∃
Свойства эквивалентности:
1) A ~ A ∀ A (рефлексивность);
2) A ~ B ⇒ B ~ A ∀ A, B (симметричность);
3) A ~ B, B ~ C ⇒ A ~ C ∀ A, B, C (транзитивность).
Всякое множество, эквивалентное множеству натуральных чисел является счетным.
Если множество счетно, то его элементы можно занумеровать.
Слайд 291.4. ЧИСЛОВЫЕ МНОЖЕСТВА.
Множество натуральных чисел N.
N = {1, 2, 3, …}.
Свойства:
1)
выполняются: коммутативность, ассоциативность, дистрибутивность;
2) деление и вычитание не определены;
3) 1 ∈ N;
4) n ∈ N ⇒ n + 1 ∈ N;
5) если M ⊆ N, 1 ∈ M, n ∈ M и (n + 1) ∈ M, то M = N (аксиома индукции);
6) N ⊂ Z счетно и бесконечно.
Слайд 30Множество целых чисел Z.
Z = { …, -2, -1, 0, 1,
Свойства:
Определены операции сложения, умножения, вычитания; Не определено деление;
Z – упорядоченно, т.е. имеет место
Z – счетно и бесконечно;
N ⊂ Z ⊂ Q.
Слайд 31Множество рациональных чисел Q.
Q = { q = p / n
Свойства:
Определены все арифметические операции;
Q – упорядоченно;
Q – плотно, т. е.
Q – счетно и бесконечно;
N ⊂ Z ⊂ Q ⊂ R.
Слайд 332.1 ПОНЯТИЕ ФУНКЦИИ. СПОСОБЫ ЗАДАНИЯ.
Пусть D – произвольное подмножество действительных чисел
Слайд 34Термины функция, отображение, преобразование – синонимы.
Обозначения: y=f(x); f: D→E;
В данной
Способы задания функций:
Аналитический, табличный, графический, программный.
Слайд 35Аналитический способ задания функций.
С помощью формул
Частное значение функции:
Область определения либо указывают
В последнем случае говорят об естественной области определения функции.
Слайд 38Неявно заданные функции:
F(x,y)=0
Если уравнение можно разрешить относительно y, то приходим к
Пример:
3x-y+2=0, y=3x+2.
Слайд 39Табличный способ задания функций.
Примеры: таблицы ln, sin и т. д.
+
- Необходимость
интерполирования.
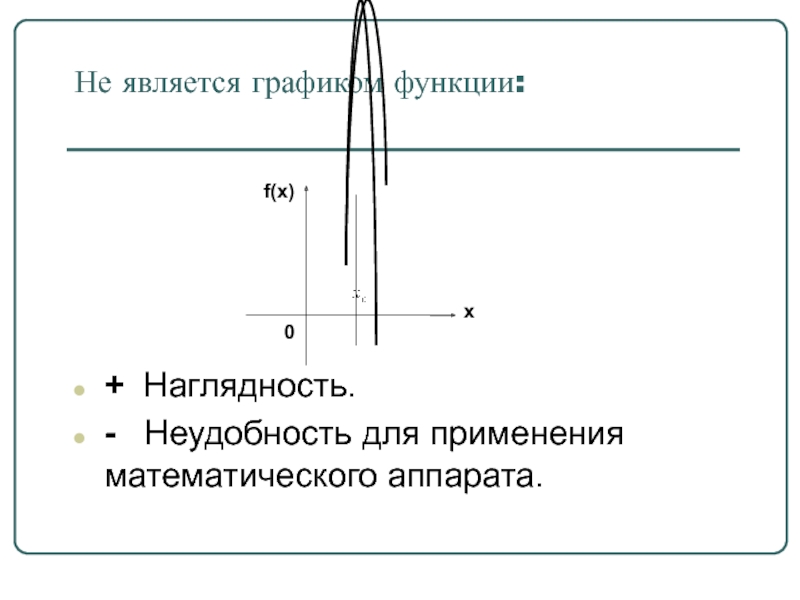
Слайд 41Не является графиком функции:
+ Наглядность.
- Неудобность для применения
Слайд 422.2 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ПОВЕДЕНИЯ ФУНКЦИЙ.
Начальный этап исследования функции.
1)
2) Четность ⇔ ∀ x∈D(f): (-x∈D(f)) ⎧⎫ (f(-x)=f(x)); нечетность ⇔ ∀ x∈D(f): (-x∈D(f)) ⎧⎫ (f(-x)=-f(x)).
Примеры:
Существуют функции общего вида.
3) Периодичность: f(x)=f(x-T)=f(x+T). T – период.
f(x) – периодическая ⇔ ∃ T≠0: ∀ x∈D(f): (x±T)∈D(f) ⎧⎫ f(x±T)=f(x).
Слайд 43
4) Монотонность: монотонно возрастающая, если
монотонно убывающая, если
5) Ограниченность:
ограниченная
ограниченная снизу ⇔ ∃ M∈R: ∀ x∈X⇒ f(x) ≥ M,
ограниченная ⇔ ∃ N,M∈R: ∀ x∈X⇒ N≤f(x)≤M.
6) Если условия пункта 5 не выполняются, то функция называется неограниченной.
Слайд 442.3 СЛОЖНАЯ ФУНКЦИЯ. ОБРАТНАЯ ФУНКЦИЯ.
Сложная функция.
На D определена функция u=ϕ(x) →
На E(u) задана y=f(u) (D(f) ⊆ E(u)).
Тогда
Называется суперпозицией функций.
x – независимая переменная; u – промежуточный аргумент.
Пример:
Слайд 45Обратная функция.
Функция y=f(x) отображает D(f) → E(f).
Рассмотрим взаимно однозначное отображение
Тогда
Пример:
Слайд 46Теорема 2.1.
Если числовая функция монотонна, то ∃ обратная функция
Это достаточное
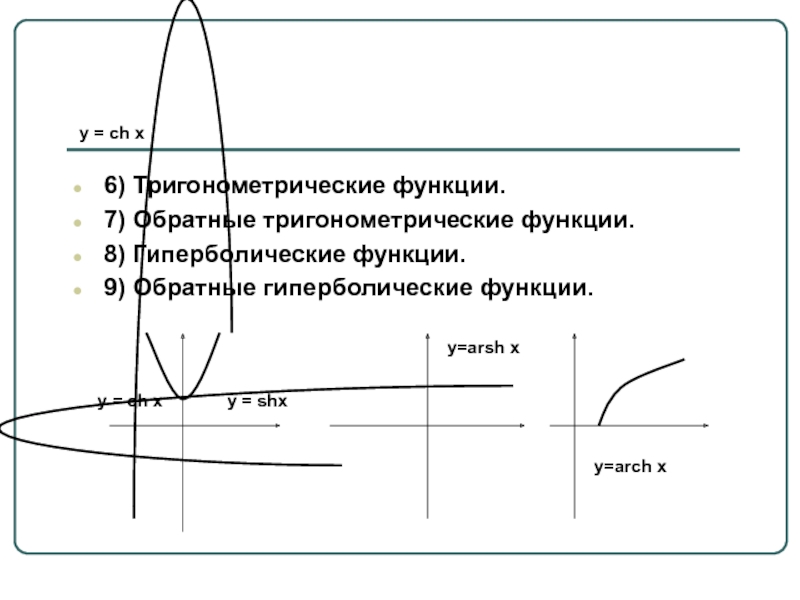
Слайд 53 y = ch x
6) Тригонометрические функции.
7) Обратные тригонометрические функции.
8) Гиперболические
9) Обратные гиперболические функции.
Слайд 552.5. КЛАССИФИКАЦИЯ ФУНКЦИЙ.
1) Целые рациональные функции:
2) Дробно-рациональные функции:
Совокупность 1) и 2)
3) Иррациональные функции: - получаются с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями.
Совокупность 1), 2) и 3) – класс алгебраических функций.
4) Трансцендентные функции: sin x, ln x, ch x и т. д.
Слайд 562.6. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ.
t – называется параметром.
Если ϕ - монотонна,
Тогда
Всякую явно заданную функцию можно представить параметрически
Слайд 58Параметрическое задание линий на плоскости.
Множество точек M(x,y) плоскости координаты которых
Прямая:





























![Аналитический способ задания функций.С помощью формулЧастное значение функции:Область определения либо указывают D(f)=[1;2], либо определяют.В последнем](/img/tmb/5/427662/6b2091a7c670fbda0837e75bbcfb2031-800x.jpg)