- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие многогранника. Призма презентация
Содержание
- 1. Понятие многогранника. Призма
- 2. Основные вопросы: Понятие многогранника и его элемента.
- 3. Многогранник или многогранная поверхность это
- 4. Грани многогранника многоугольники, из которых составлен
- 5. МНОГОГРАННИКИ бывают Многогранник расположен
- 6. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Выпуклый многогранник называется правильным,
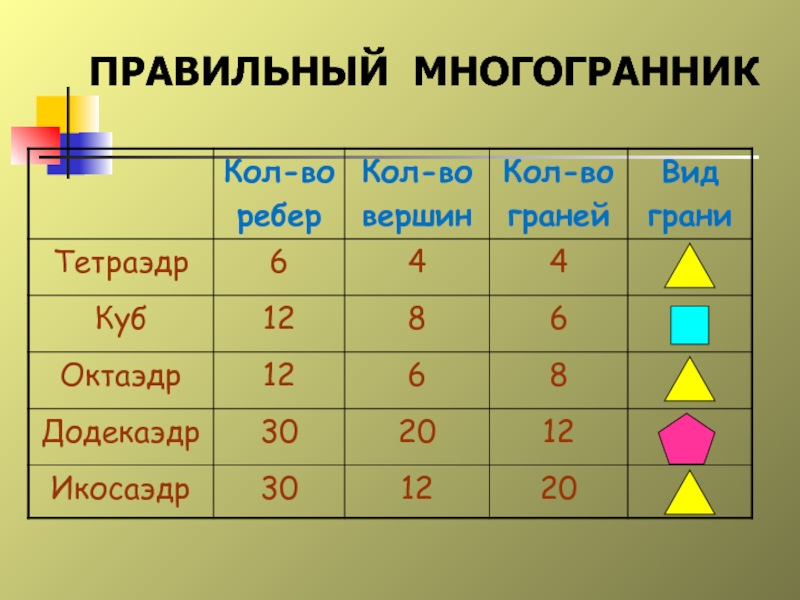
- 7. ПРАВИЛЬНЫЙ МНОГОГРАННИК
- 8. Рассмотрим два равных многоугольника А1А2….Аn
- 9. Каждый из n- четырехугольников:
- 10. Многогранник,
- 11. Многоугольники
- 12. Призму с основаниями А1А2… Аn и
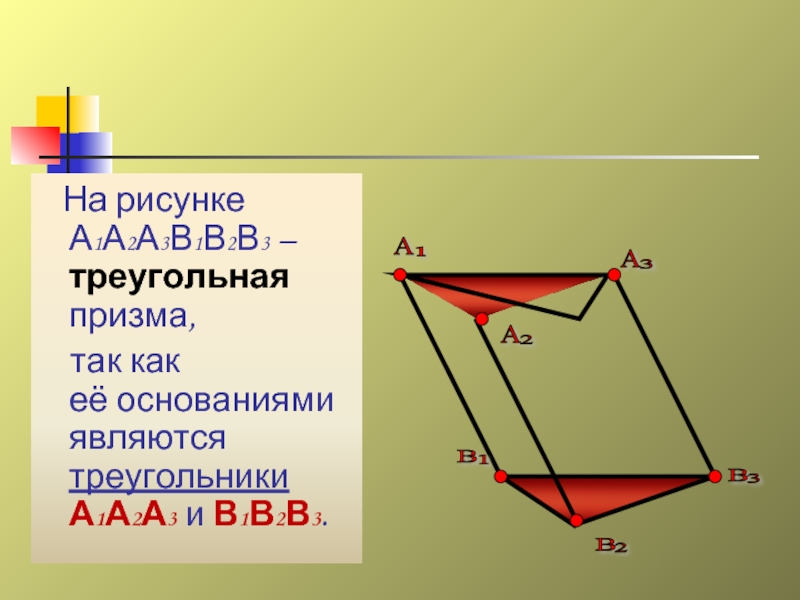
- 13. На рисунке А1А2А3В1В2В3 –треугольная призма,
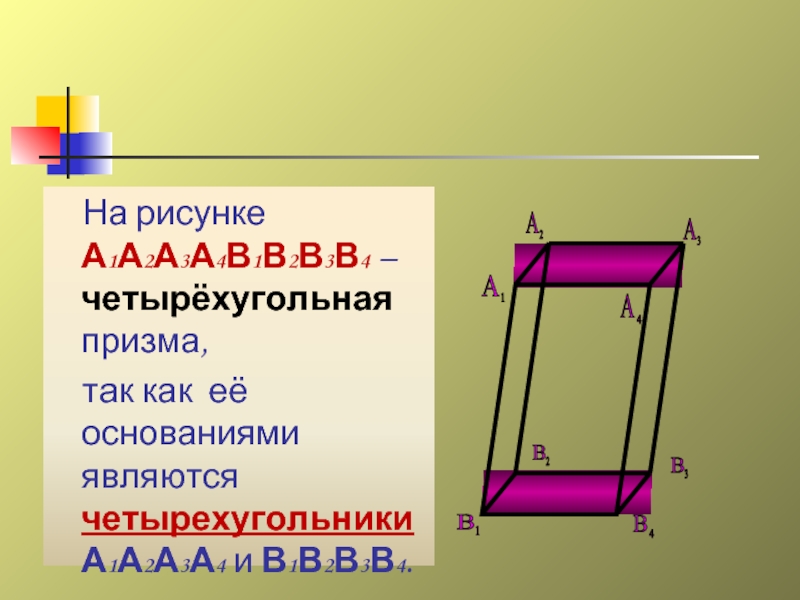
- 14. На рисунке А1А2А3А4В1В2В3В4
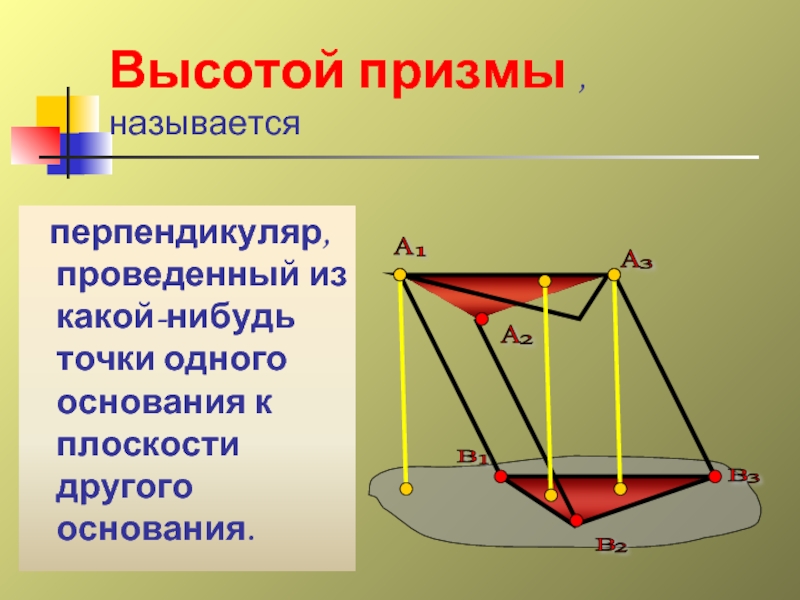
- 15. перпендикуляр, проведенный из какой-нибудь
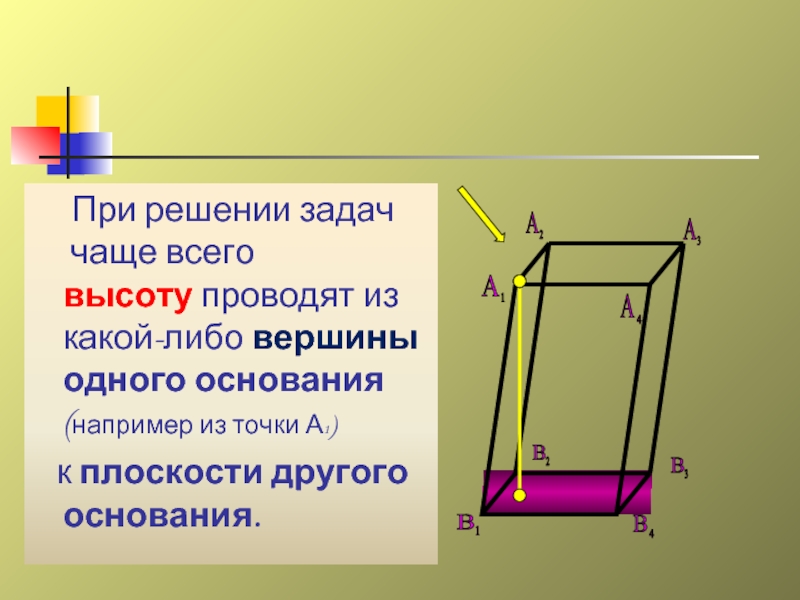
- 16. При решении задач
- 17. Призма называется прямой,
- 18. Наклонной называют такую призму, боковые ребра которой не будут перпендикулярны к основаниям.
- 19. Правильной призмой называют прямую призму, если её основания – правильные многоугольники.
- 20. Свойства правильной призмы 1. Основания правильной
- 21. Примеры правильных призм. шестиугольная
- 22. правильная четырехугольная призма, в
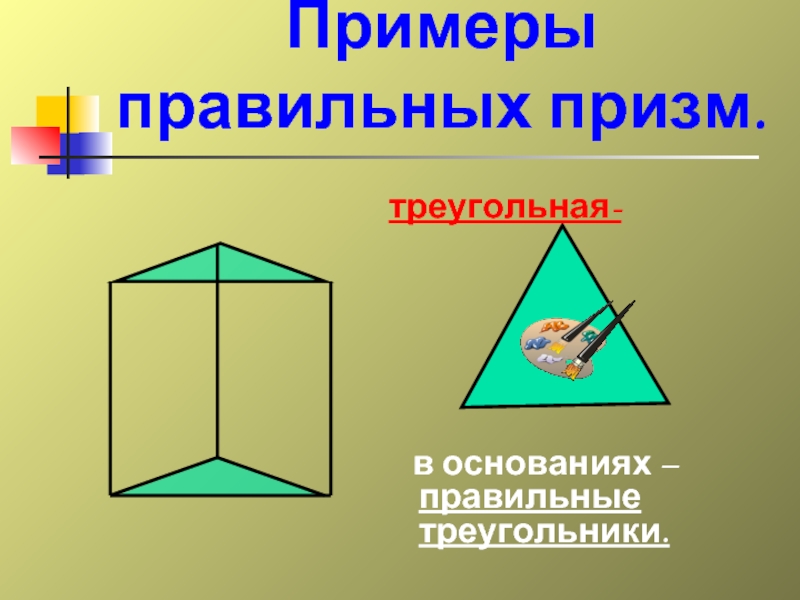
- 23. треугольная-
- 24. Поверхность призмы состоит из двух оснований и боковой поверхности.
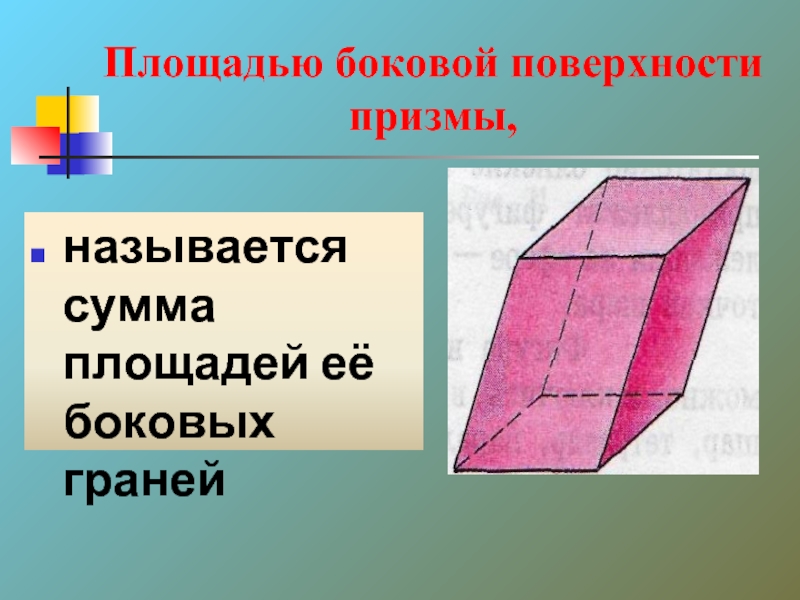
- 25. Площадью боковой поверхности призмы, называется сумма площадей её боковых граней
- 26. Площадью полной поверхности призмы называется сумма площадей всех её граней.
- 27. Теорема о боковой поверхности прямой призмы Площадь
- 28. Сечение призмы плоскостью, проведенной через два боковых
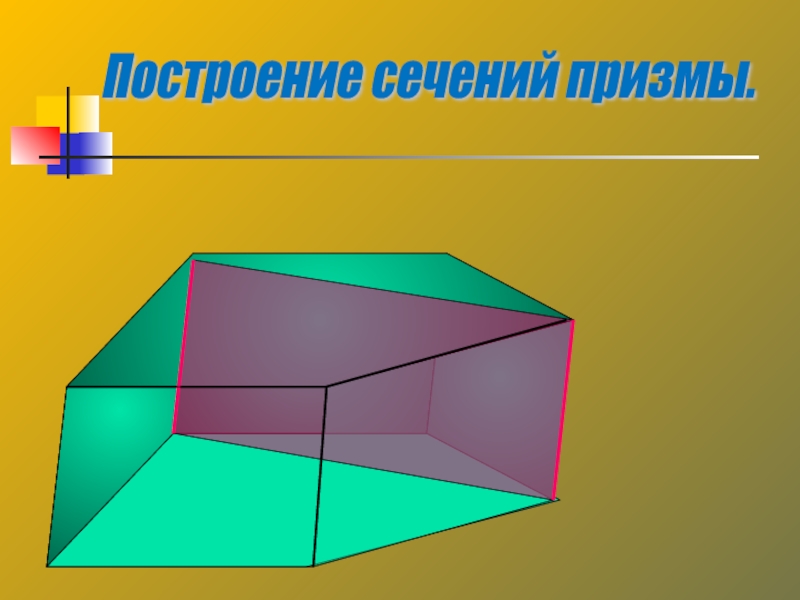
- 29. Построение сечений призмы.
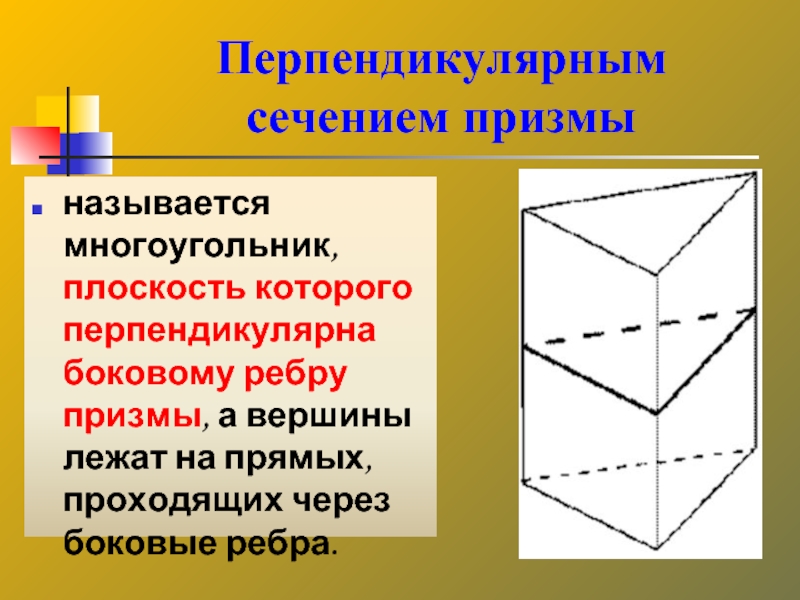
- 30. Перпендикулярным сечением призмы называется многоугольник, плоскость которого
Слайд 2Основные вопросы:
Понятие многогранника и его элемента.
Призма и её виды.
Определение призмы и
Основные свойства призм.
Описание поверхности призмы (основания и боковая поверхность).
Определение высоты и диагонали призмы.
Теорема о боковой поверхности призмы.
Сечения призмы плоскостью.
Слайд 3Многогранник
или многогранная поверхность
это поверхность, составленная из многоугольников и ограничивающая
Примеры многогранников
Тетраэдр – поверхность, составленная из четырёх треугольников
Параллелепипед – поверхность, составленная из шести параллелограммов
Октаэдр – поверхность, составленная из восьми треугольников
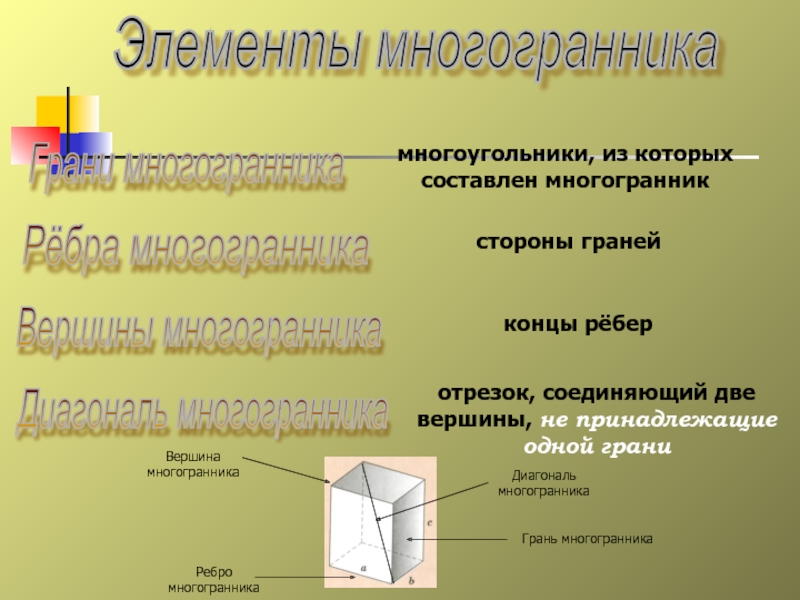
Слайд 4Грани многогранника
многоугольники, из которых составлен многогранник
Элементы многогранника
Рёбра многогранника
стороны
концы рёбер
Вершины многогранника
Диагональ многогранника
отрезок, соединяющий две вершины, не принадлежащие одной грани
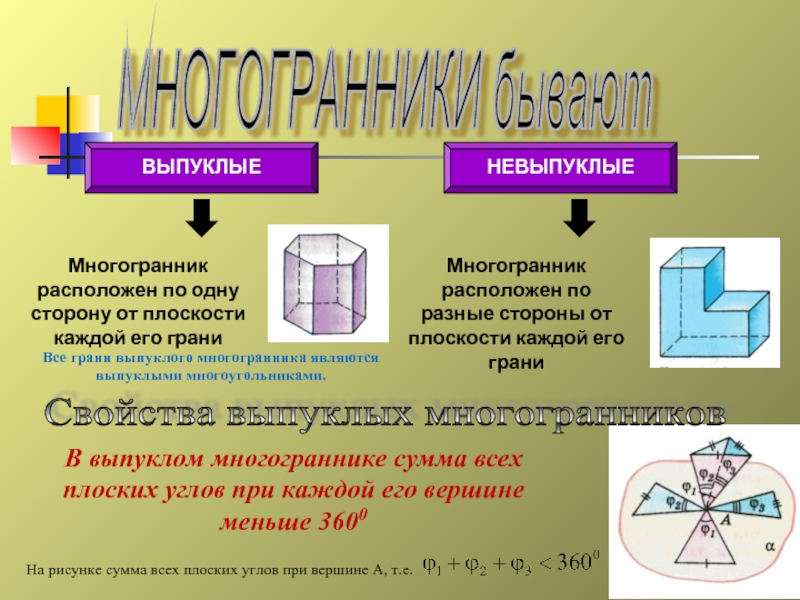
Слайд 5МНОГОГРАННИКИ бывают
Многогранник расположен по одну сторону от плоскости каждой его
Многогранник расположен по разные стороны от плоскости каждой его грани
Все грани выпуклого многогранника являются выпуклыми многоугольниками.
В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600
Свойства выпуклых многогранников
Слайд 6ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если все его грани –
правильный тетраэдр
правильный октаэдр
правильный икосаэдр
куб
правильный додекаэдр
правильный тетраэдр: составлен из четырёх равносторонних треугольников, сумма плоских углов при вершине 1800;
правильный октаэдр: составлен из восьми равносторонних треугольников, сумма плоских углов при вершине 2400;
правильный икосаэдр: составлен ид двадцати равносторонних треугольников, сумма плоских углов при вершине 3000;
куб: составлен из шести квадратов, сумма плоских углов при вершине 2700;
правильный додекаэдр: составлен из двенадцати правильных пятиугольников, сумма плоских углов при вершине 3240
Слайд 8
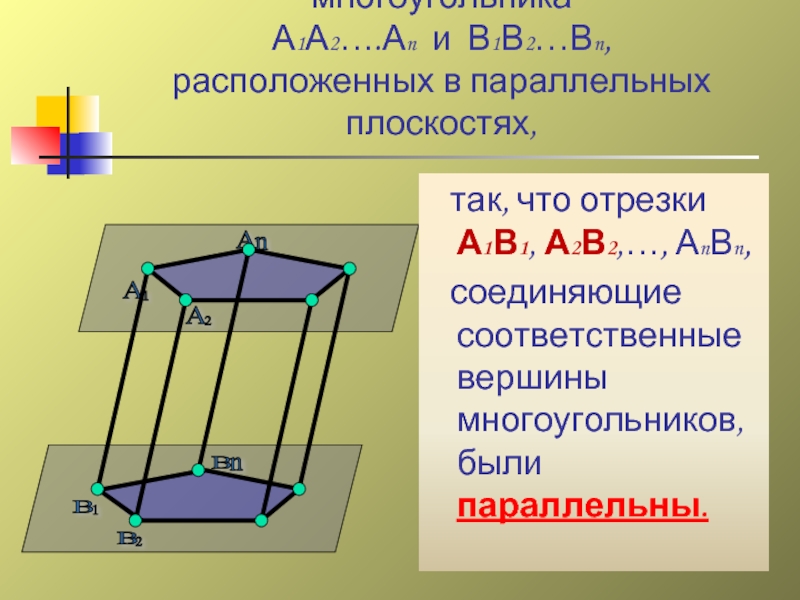
Рассмотрим два равных многоугольника
А1А2….Аn и В1В2…Вn,
расположенных в параллельных плоскостях,
соединяющие соответственные вершины многоугольников, были параллельны.
Слайд 9
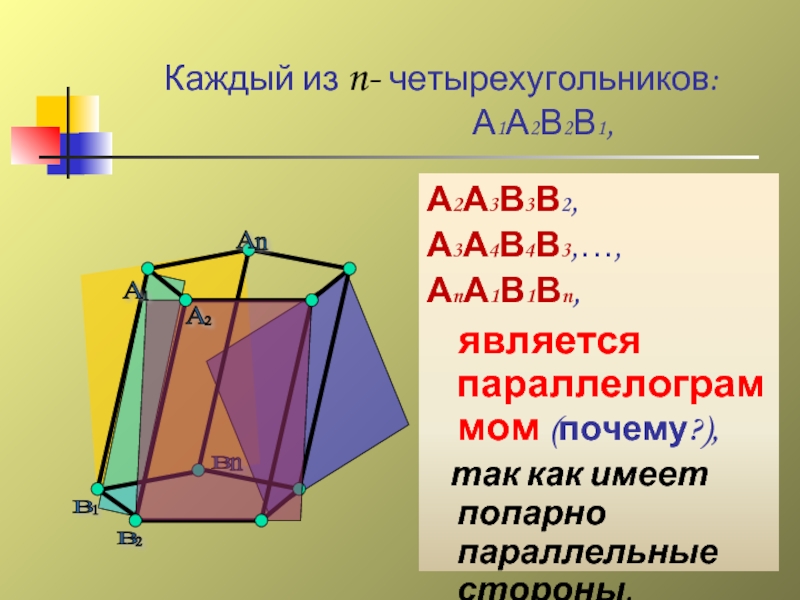
Каждый из n- четырехугольников:
А2А3В3В2,
А3А4В4В3,…,
АnА1В1Вn,
является параллелограммом (почему?),
так как имеет попарно параллельные стороны.
Слайд 10
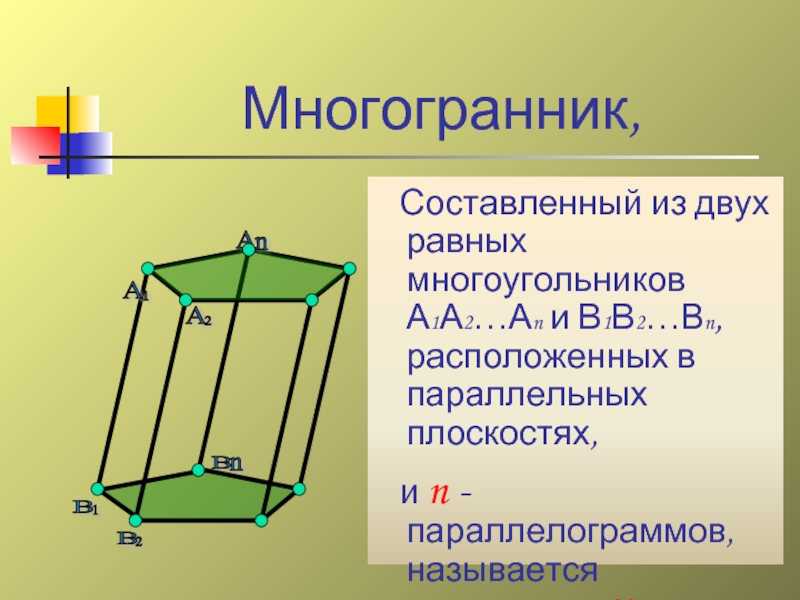
Многогранник,
Составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn,
и n -параллелограммов, называется призмой.
Слайд 11
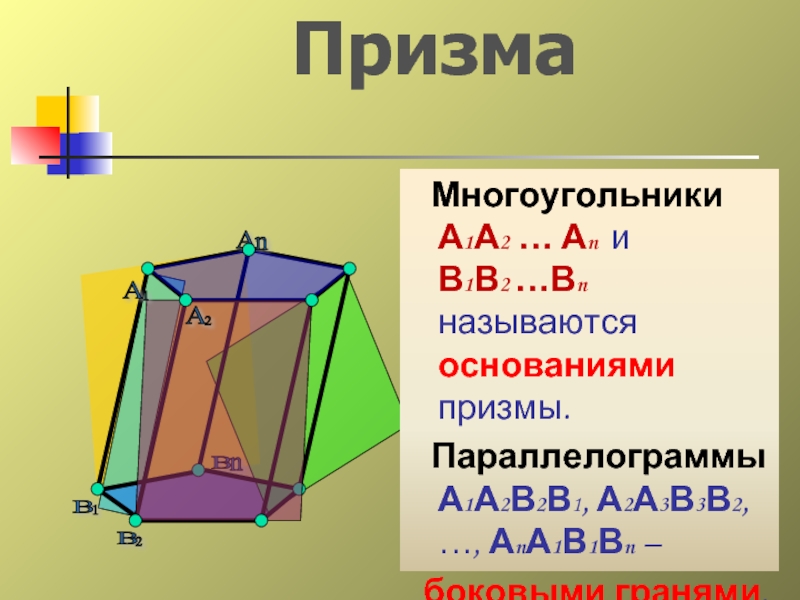
Многоугольники
А1А2 … Аn и
В1В2 …Вn называются основаниями
Параллелограммы А1А2В2В1, А2А3В3В2, …, АnА1В1Вn –
боковыми гранями.
Призма
Слайд 12Призму с основаниями А1А2… Аn и В1В2 …Вn обозначают А1А2…АnВ1В2…Вn и
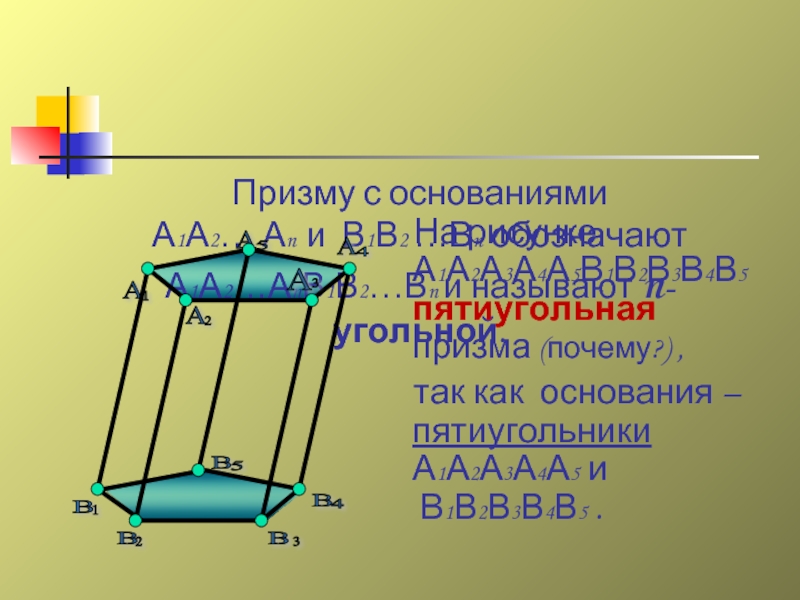
На рисунке
А1А2А3А4А5В1В2В3В4В5
пятиугольная
призма (почему?) ,
так как основания – пятиугольники А1А2А3А4А5 и
В1В2В3В4В5 .
Слайд 13 На рисунке А1А2А3В1В2В3 –треугольная призма,
так как
её
Слайд 14
На рисунке А1А2А3А4В1В2В3В4 – четырёхугольная призма,
так как
Слайд 15
перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости
Высотой призмы , называется
Слайд 16
При решении задач
чаще всего
высоту проводят из
к плоскости другого основания.
Слайд 17
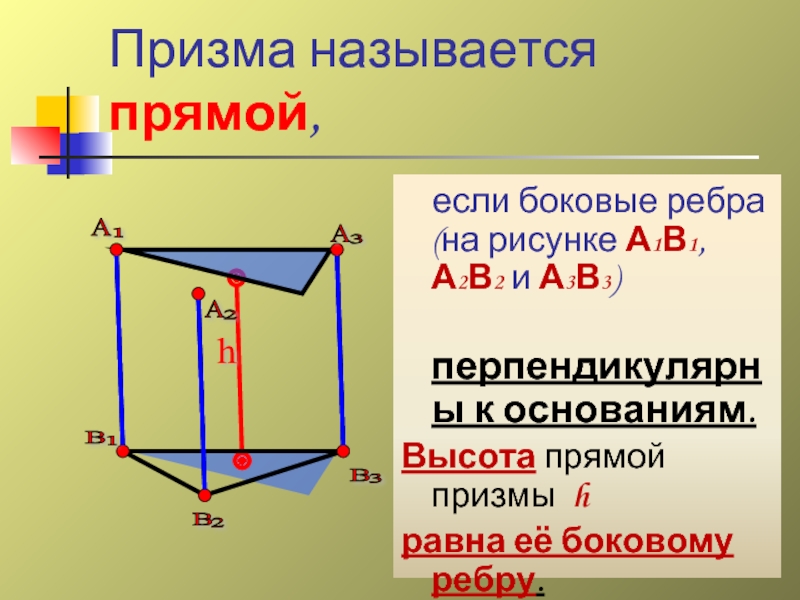
Призма называется прямой,
если боковые ребра (на рисунке А1В1, А2В2
перпендикулярны к основаниям.
Высота прямой призмы h
равна её боковому ребру.
h
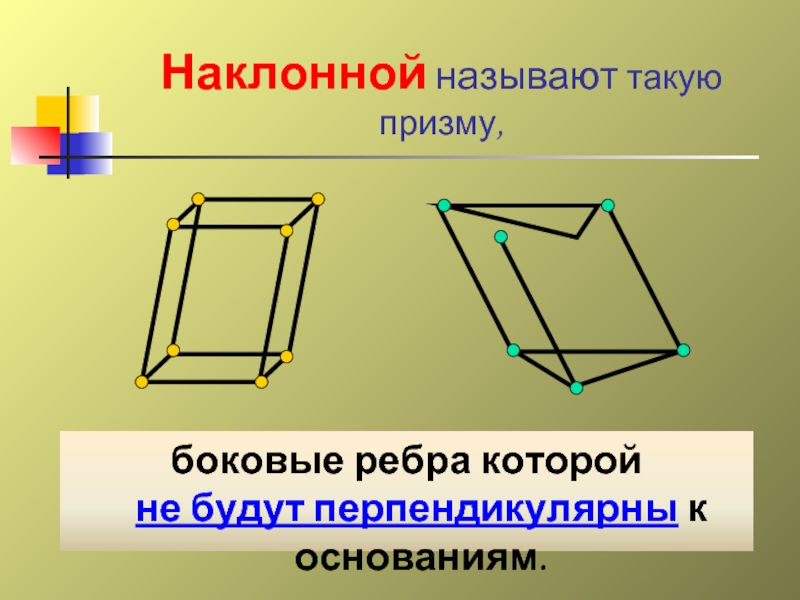
Слайд 18Наклонной называют такую призму,
боковые ребра которой
не будут перпендикулярны к основаниям.
Слайд 20Свойства правильной призмы
1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной
3. Боковые ребра правильной призмы параллельны и равны.
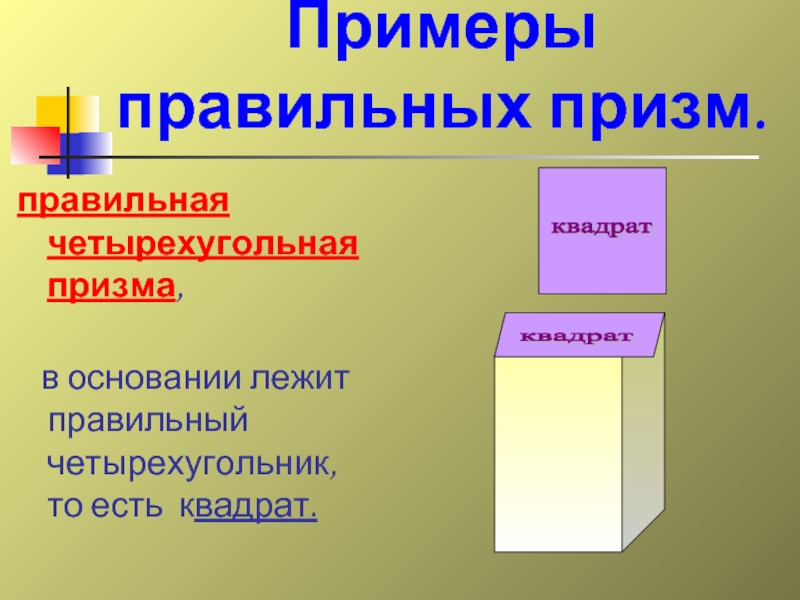
Слайд 22правильная четырехугольная призма,
в основании лежит правильный четырехугольник,
то есть
квадрат
квадрат
Примеры правильных призм.
Слайд 27Теорема о боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмы равна
Sбок. = Ph
Слайд 28Сечение призмы плоскостью, проведенной через два боковых ребра, не принадлежащих одной
В сечении образуется параллелограмм. В некоторых случаях может получаться ромб, прямоугольник или квадрат
Сечения призмы
Слайд 30Перпендикулярным сечением призмы
называется многоугольник, плоскость которого перпендикулярна боковому ребру призмы, а
