- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью презентация
Содержание
- 1. Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
- 2. Часть 5: Распараллеливание на компьютерах с распределенной памятью Linpack LAPACK DAG алгоритм
- 3. Blas Basic Linear Algebra Subprograms - BLAS
- 4. Linpack Linear Algebra Package Пакет для
- 5. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 6. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 7. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 8. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 9. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 10. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 11. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 12. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 14. Linpack Плюсы: Достаточно оптимизировать BLAS
- 15. LAPACK Linear Algebra Package Пакет для
- 17. LAPACK Плюсы: Достаточно оптимизировать BLAS
- 18. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 19. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 20. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 21. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 22. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 23. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 24. Dag подход (Directed acyclic graph) L11
- 25. Dag подход (Directed acyclic graph) L11 L12 L13 L14
- 26. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22
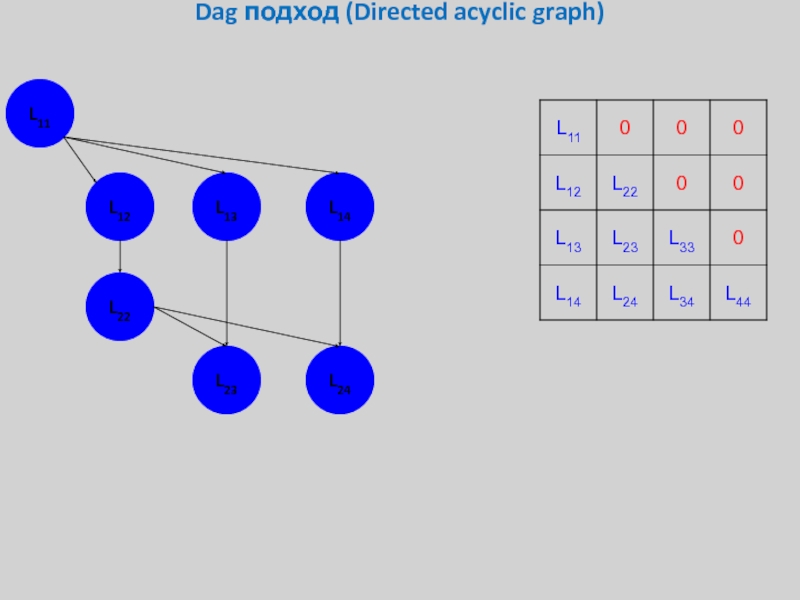
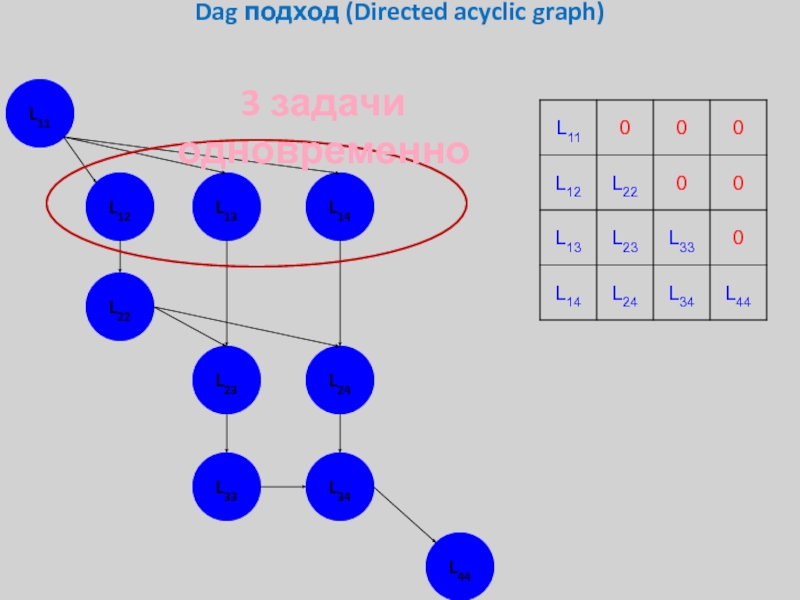
- 27. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24
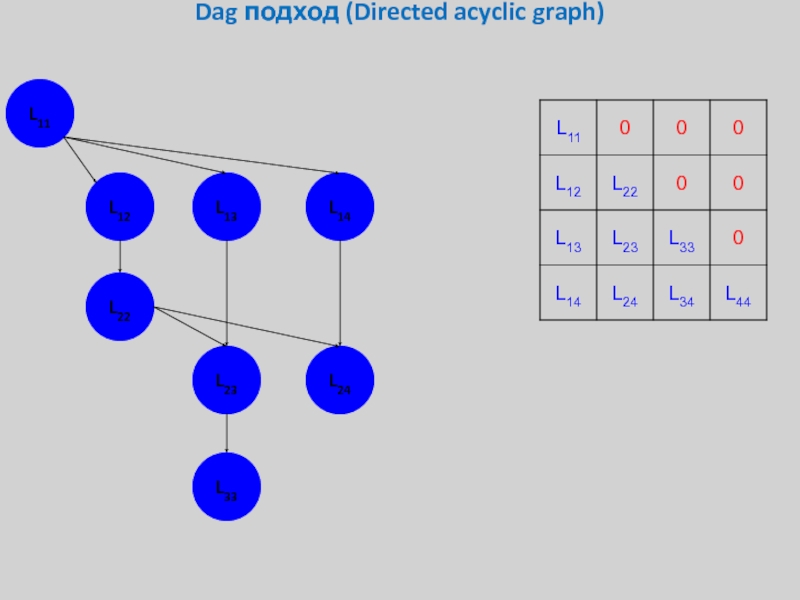
- 28. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33
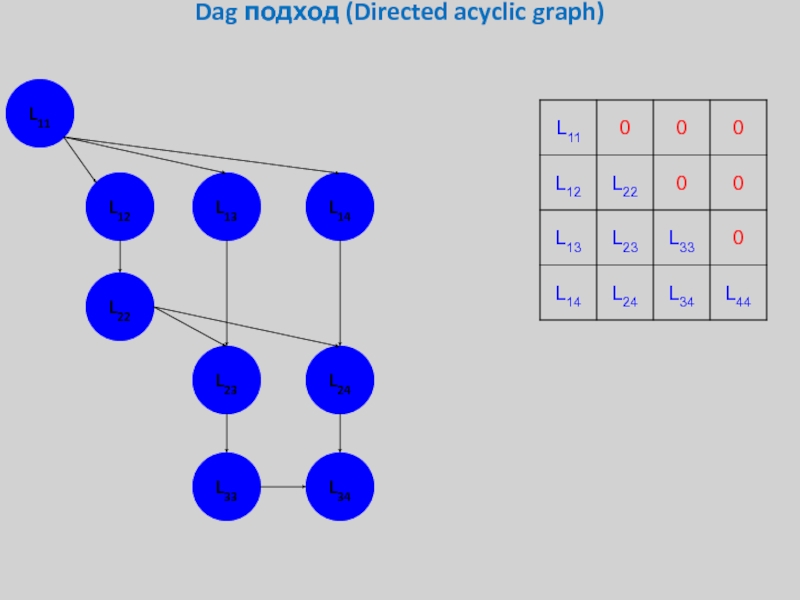
- 29. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33 L34
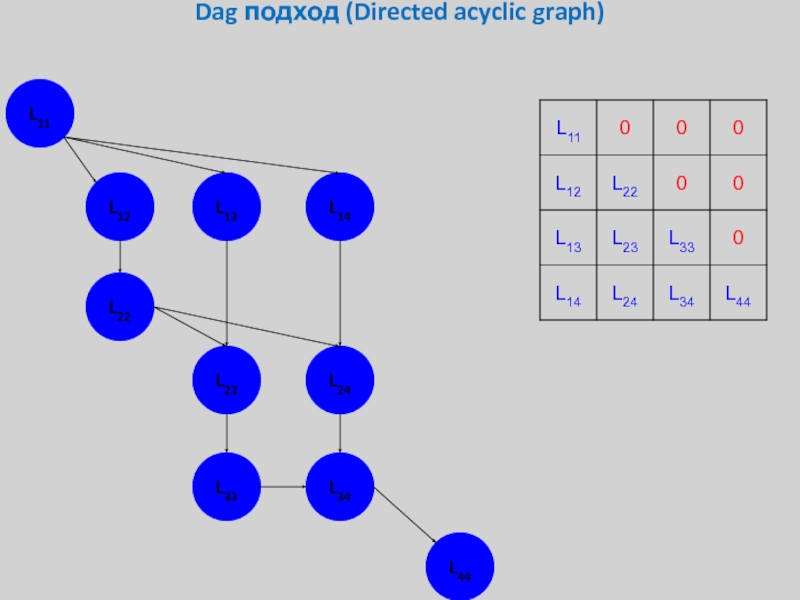
- 30. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33 L34 L44
- 31. Dag подход (Directed acyclic graph) L11 L12
- 32. Dag подход (Directed acyclic graph) Более того,
- 33. Dag подход (Directed acyclic graph)
- 34. Dag подход (Directed acyclic graph)
- 35. Dag подход (Directed acyclic graph)
- 36. Dag подход (Directed acyclic graph)
- 37. Dag подход (Directed acyclic graph)
- 38. Dag подход (Directed acyclic graph)
- 39. Dag подход (Directed acyclic graph)
- 40. Dag подход (Directed acyclic graph)
- 41. Dag подход (Directed acyclic graph)
- 42. Dag подход (Directed acyclic graph)
- 43. Dag подход (Directed acyclic graph)
- 44. Dag подход (Directed acyclic graph) Плюсы:
- 45. Далее... Как реализовать алгорититм для
- 46. Вопросы и Ответы
Слайд 1Спецкурс кафедры «Вычислительной математки»
Параллельные алгоритмы вычислительной алгебры
Александр Калинкин
Сергей Гололобов
Слайд 3Blas
Basic Linear Algebra Subprograms
- BLAS Level 1 – операции с векторами
- BLAS Level 2 – матрично-векторные операции (умножение матрицы разных типов на вектор)
- BLAS Level 3 – операции с матрицами (перемножение прямоугольных матриц различных типов)
Опубликован в 1979 году
В свободном доступе на netlib.org
Содержится в оптимизированном виде в огромном количестве математических библиотек (Intel MKL, ACML, ATLAS, и тд)
Слайд 4Linpack
Linear Algebra Package
Пакет для решения систем линейных уравнений и задачи
Опубликован в конце 70-х годов Джеком Донгарра с коллективом
В свободном доступе на netlib.org
Впоследствии пакет стал основной замером производительности кластеров, в частности top500 определяются по модификации этого пакета.
Основная функциональность – разложение Холесского, в симметричном случае представление матрицы
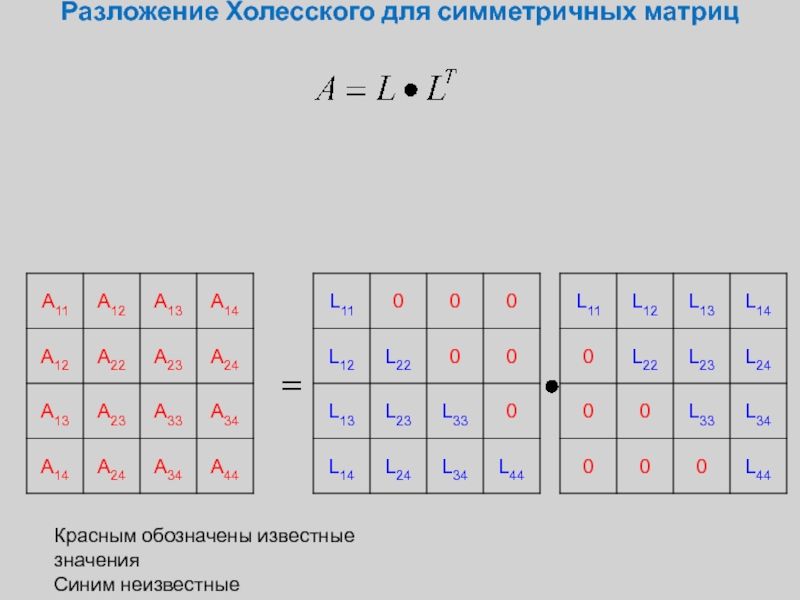
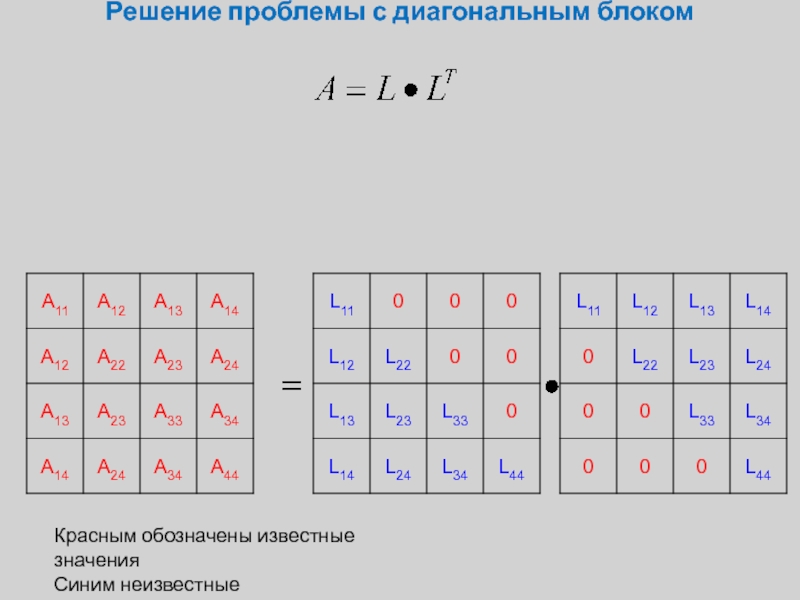
Слайд 5Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
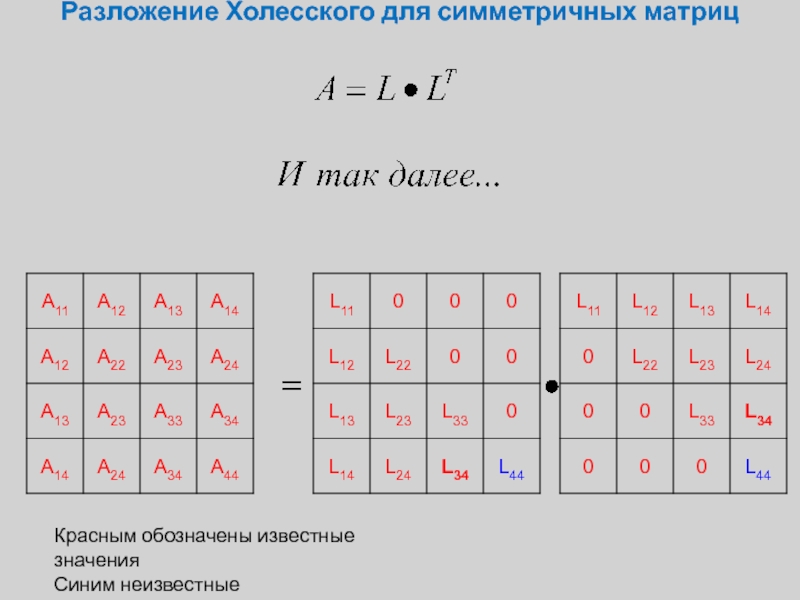
Слайд 6Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
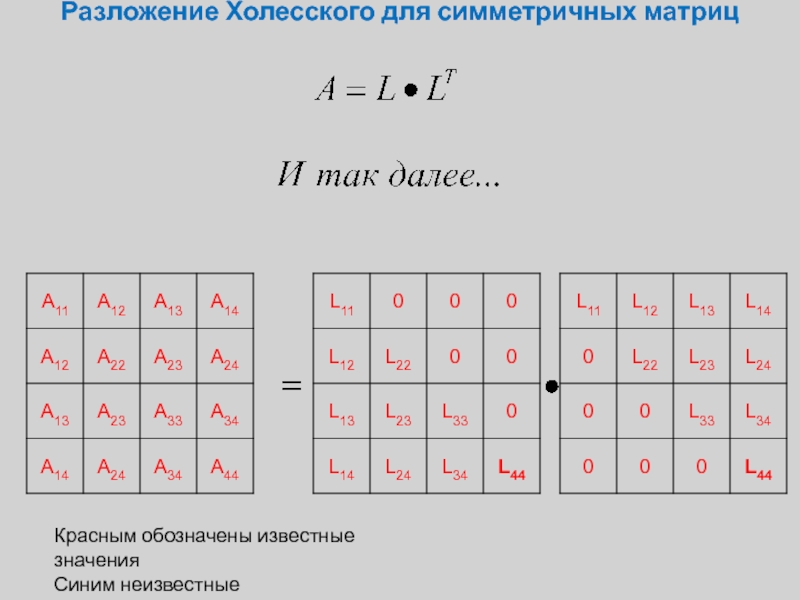
Слайд 7Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
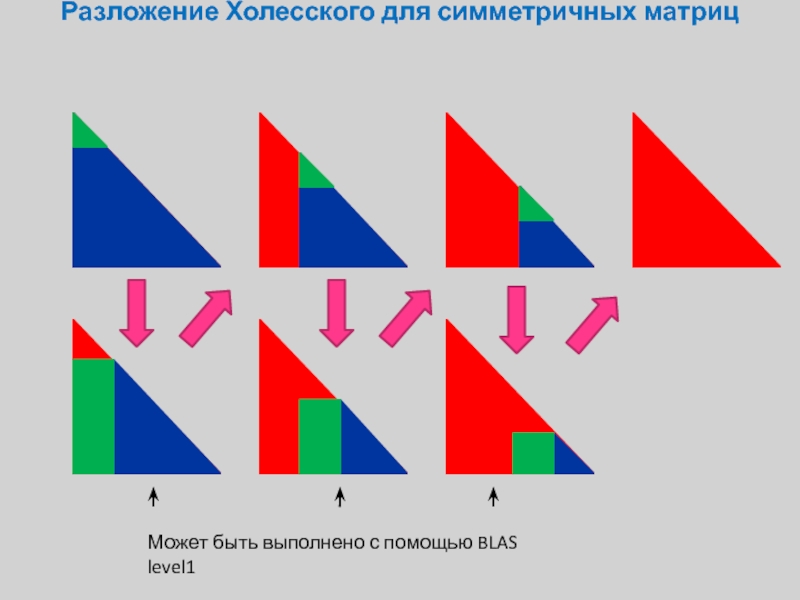
Слайд 8Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 9Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 10Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 11Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 12Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 14Linpack
Плюсы:
Достаточно оптимизировать BLAS level 1 для процессора, чтоб получить оптимизированный
Минусы:
При увеличении кэша становится неэффективно умножать только строку на число – кэш значительно больше, есть возможность использовать его более разумно
После каждого использования BLAS level 1 приходится вычислять корень из 1 вещественного числа – неэффективно для современныю процессоров
Blas level 1 не очень хорошо параллелизуется, появление многоядерных процессоров накладывает свои требования
Слайд 15LAPACK
Linear Algebra Package
Пакет для решения систем линейных уравнений, поиска сингулярных
Опубликован в конце 1992 году Джеком Донгарра с коллективом
В свободном доступе на netlib.org
Содержится в оптимизированном виде в огромном количестве математических библиотек (Intel MKL, ACML, ATLAS, и тд)
Содержит параллельную версию разложения Холесского
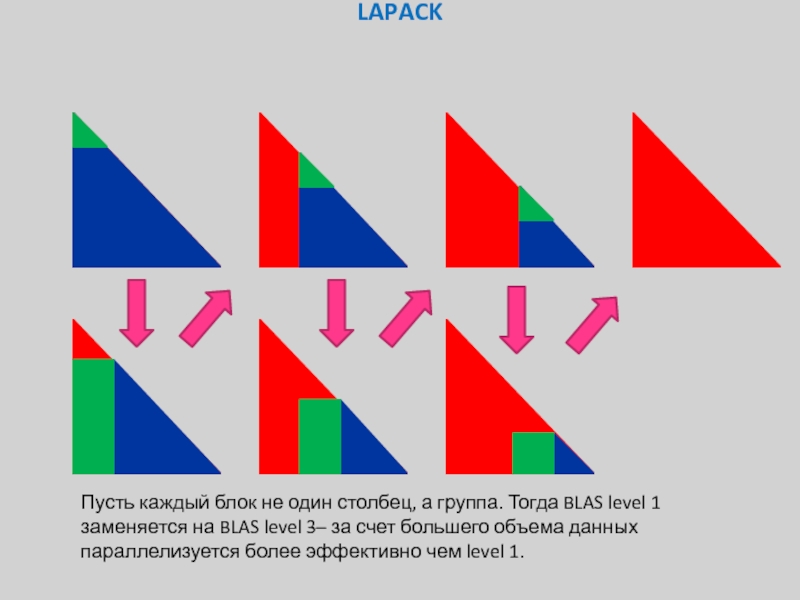
Слайд 16
LAPACK
Пусть каждый блок не один столбец, а группа. Тогда BLAS level
Слайд 17LAPACK
Плюсы:
Достаточно оптимизировать BLAS level 3 для процессора, чтоб получить оптимизированное
Минусы:
Не такая эффективная работа на процессорах с разным уровнем кэша – постоянно приходится перекачивать данные с уровня на уровень.
Каждый эффективный вызов BLAS level 3 чередуется с неэффективным вызовом LLT разложения для диагонального блока.
При большом числе процессоров возникает ограничение на “шкалирование” вычисления группы столбов – если группа большая, то время на вычисление диагонального блока станосится существенным.
Слайд 18Решение проблемы с диагональным блоком
Красным обозначены известные значения
Синим неизвестные
Слайд 19Решение проблемы с диагональным блоком
Красным обозначены известные значения
Синим неизвестные
Слайд 20Решение проблемы с диагональным блоком
Красным обозначены известные значения
Синим неизвестные
Слайд 21Решение проблемы с диагональным блоком
Красным обозначены известные значения
Синим неизвестные
Слайд 22Разложение Холесского для симметричных матриц
Красным обозначены известные значения
Синим неизвестные
Слайд 23Решение проблемы с диагональным блоком
Красным обозначены известные значения
Синим неизвестные
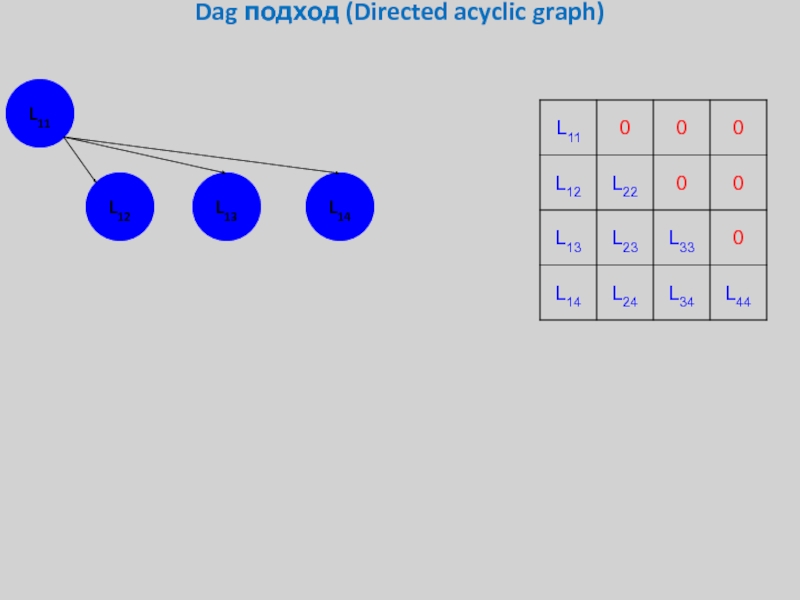
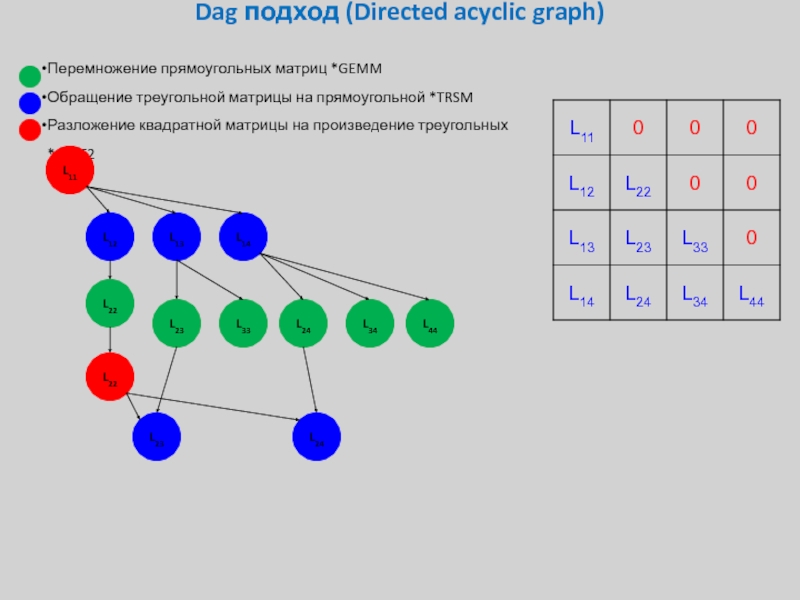
Слайд 32Dag подход (Directed acyclic graph)
Более того, мы можем постепенно модифицировать
Lij, а
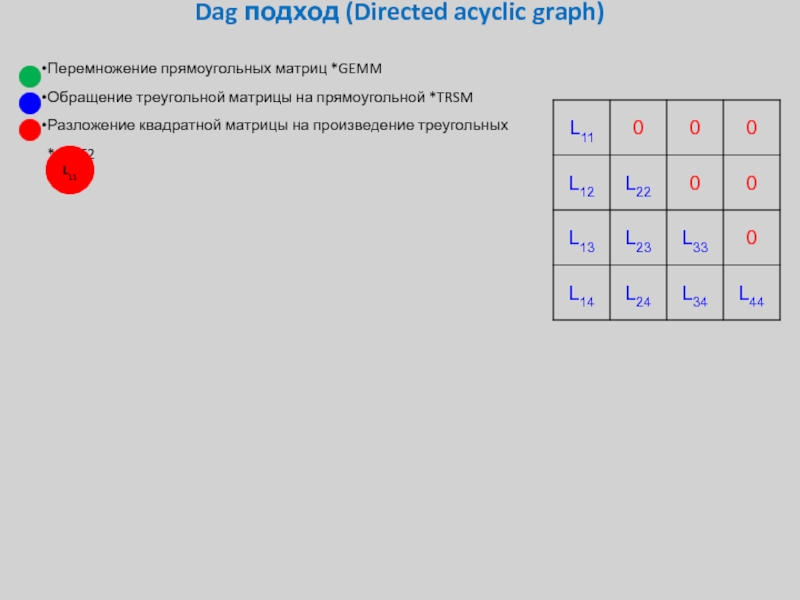
Слайд 33Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
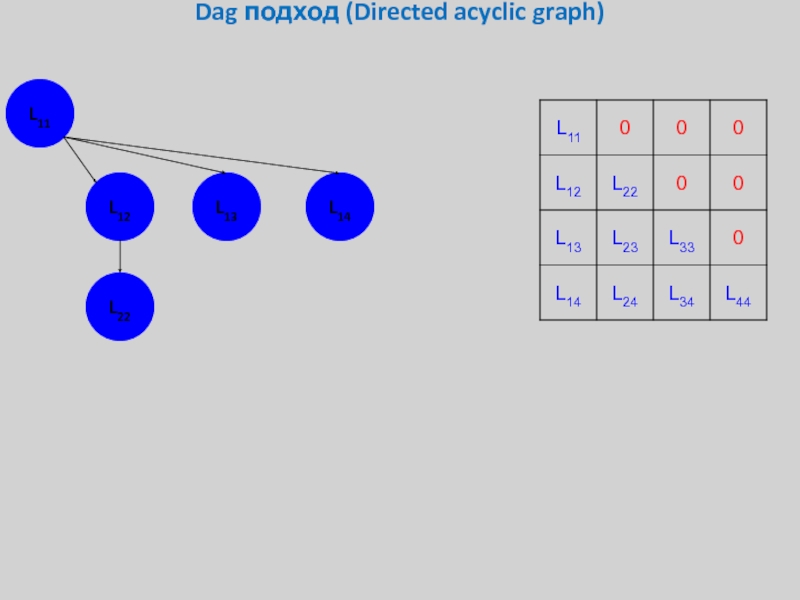
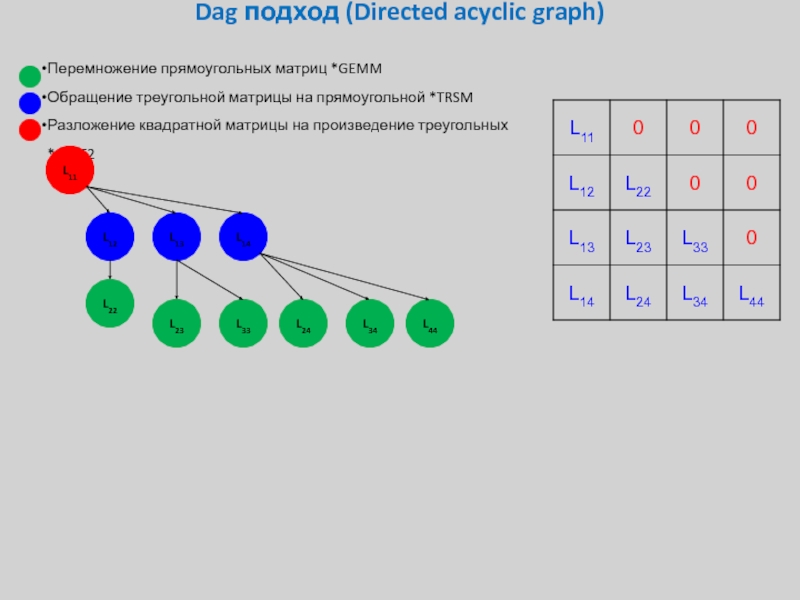
Слайд 34Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
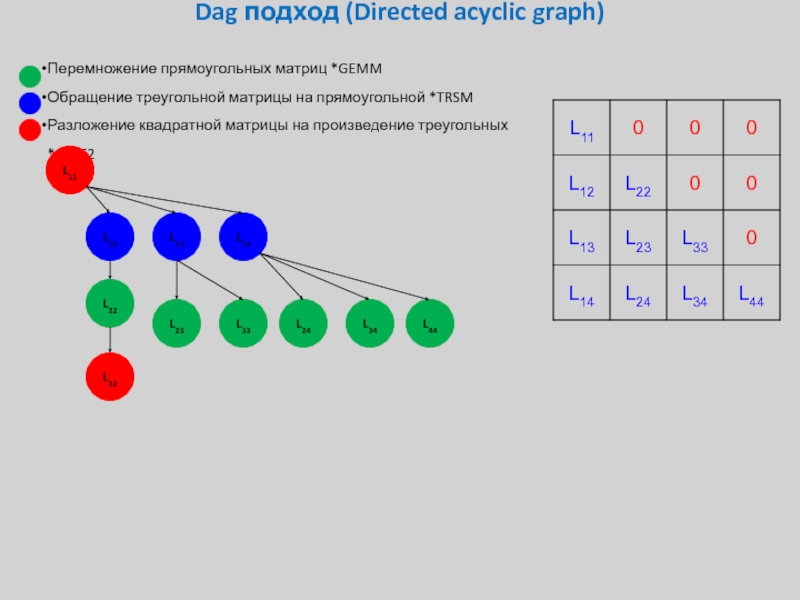
Слайд 35Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
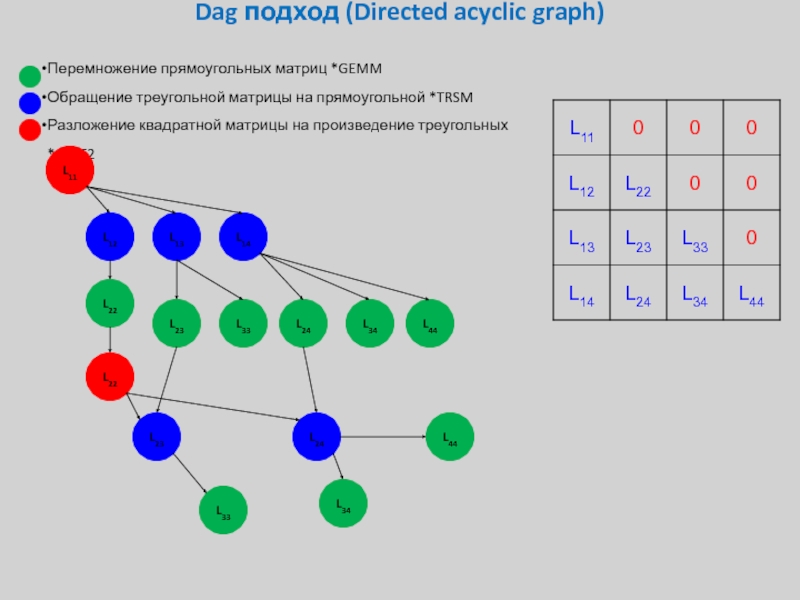
Слайд 36Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
Слайд 37Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
Слайд 38Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L34
L44
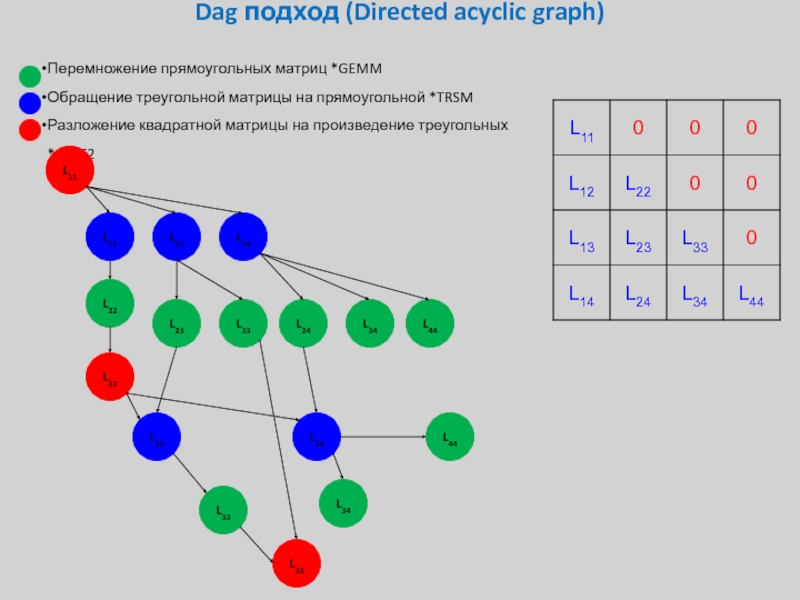
Слайд 39Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L33
L34
L44
Слайд 40Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L33
L34
L44
L34
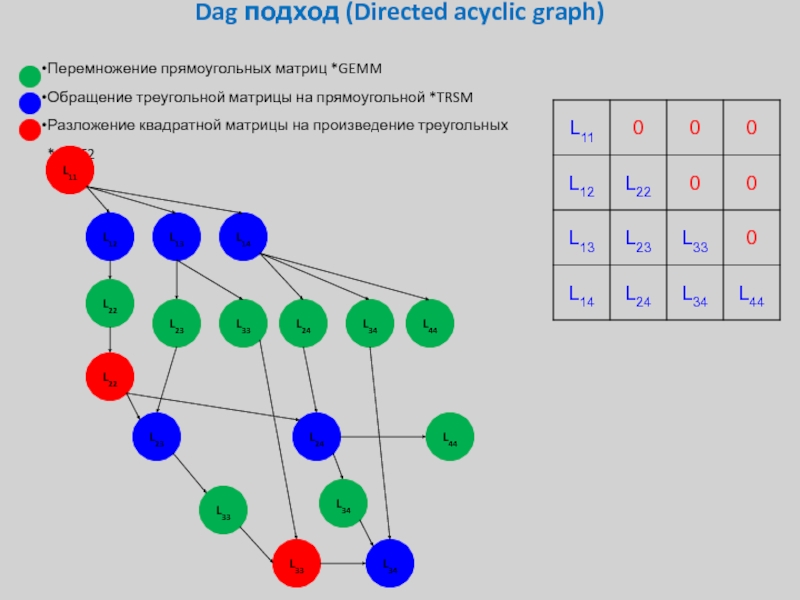
Слайд 41Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L33
L34
L44
L34
L44
Слайд 42Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L33
L34
L44
L44
L34
L44
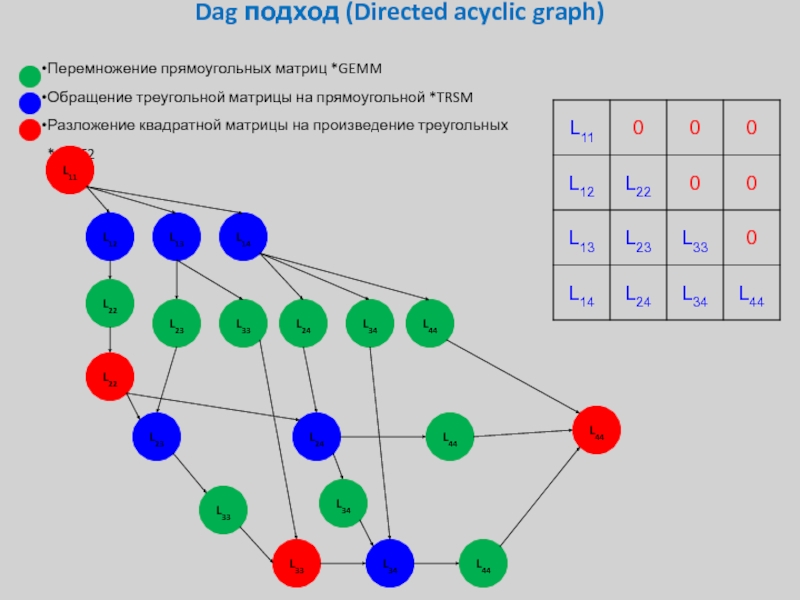
Слайд 43Dag подход (Directed acyclic graph)
Перемножение прямоугольных матриц *GEMM
Обращение треугольной матрицы на
Разложение квадратной матрицы на произведение треугольных *GETF2
L11
L12
L13
L14
L22
L23
L33
L24
L34
L44
L22
L23
L24
L33
L33
L34
L44
L44
L34
L44
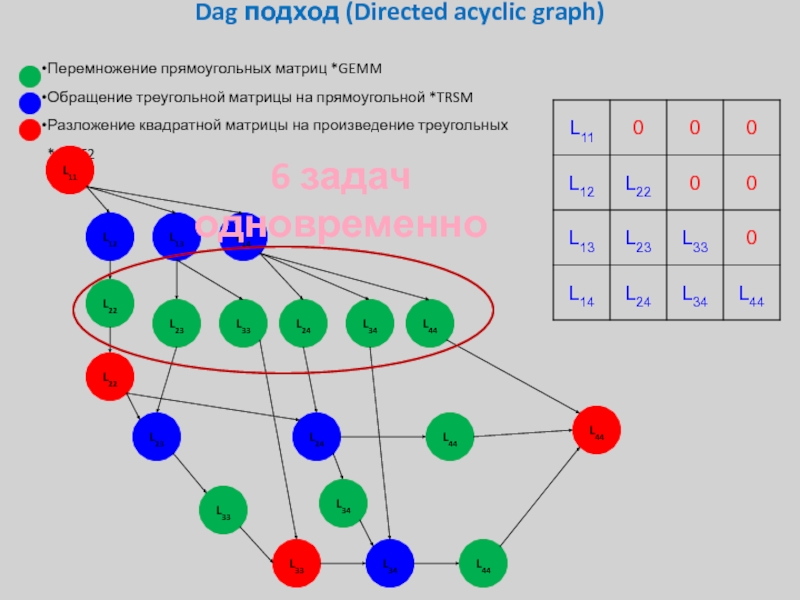
6 задач одновременно
Слайд 44Dag подход (Directed acyclic graph)
Плюсы:
Очень хорошая шкалируемость на старте алгоритма
Динамическое
Возможность изменения размеров блоков в зависимости от положения в графе
Минусы:
Слабая шкалируемость на окончании алгоритма
Динамическое распределение задач
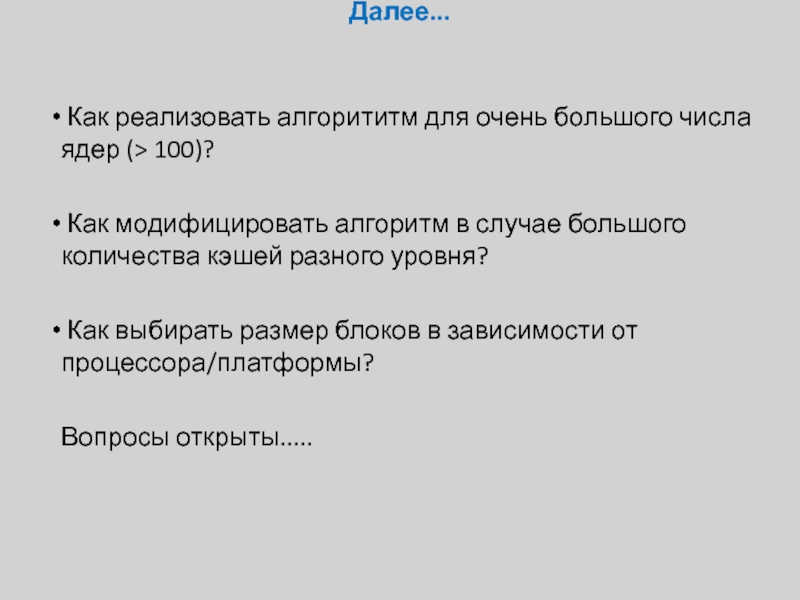
Слайд 45Далее...
Как реализовать алгорититм для очень большого числа ядер (> 100)?
Как выбирать размер блоков в зависимости от процессора/платформы?
Вопросы открыты.....