- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ГИА. Решение заданий презентация
Содержание
- 1. Подготовка к ГИА. Решение заданий
- 2. Какие из следующих утверждений верны? 1
- 3. Два угла называются вертикальными, если стороны
- 4. Две прямые либо имеют только одну
- 5. Не всегда через три точки можно
- 6. Перпендикуляр, проведённый из точки к прямой,
- 7. Какие из следующих утверждений верны? 1
- 8. Если при пересечении двух прямых
- 9. Сумма смежных углов равна 1800. Два
- 10. Если при пересечении двух прямых
- 11. Не всегда через три точки можно
- 12. Какие из следующих утверждений верны? 3.
- 13. Если расстояние между центрами двух
- 14. Угол, вершина которого лежит на окружности,
- 15. Вписанный угол измеряется половиной дуги, на
- 16. 1 С А В
- 17. Часть 1. Модуль «Алгебра»
- 18. Часть 1. Модуль «Алгебра» Ответ: 3 2 1 3
- 19. Часть 1. Модуль «Алгебра» Ответ: 1
- 20. Часть 1. Модуль «Алгебра»
- 21. Часть 1. Модуль «Алгебра»
- 22. Часть 1. Модуль «Алгебра» Ответ:
- 23. Часть 1. Модуль «Алгебра» Ответ: 1/3
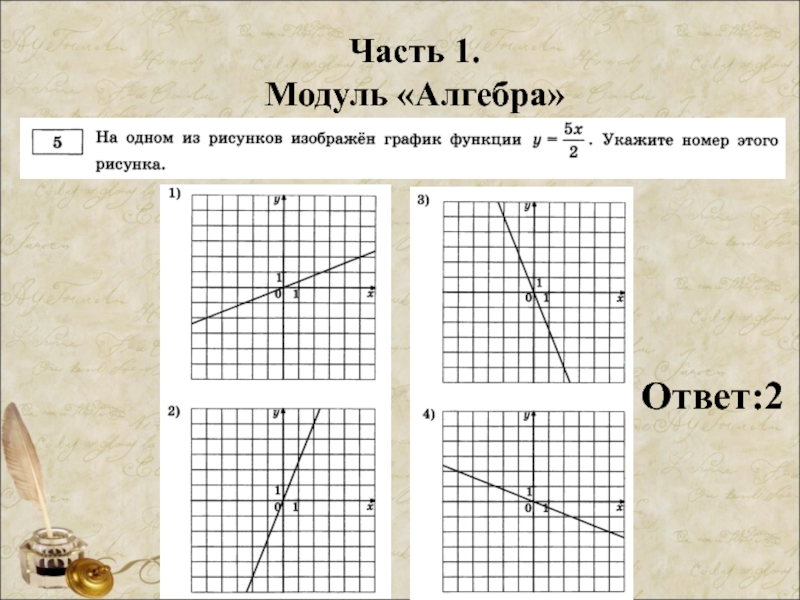
- 24. Часть 1. Модуль «Алгебра» Ответ:2
- 25. Часть 1. Модуль «Алгебра» Ответ: 2
- 26. Часть 1. Модуль «Алгебра» Ответ:
- 27. Часть 1. Модуль «Алгебра» Ответ: х Є (-∞; -1,25]
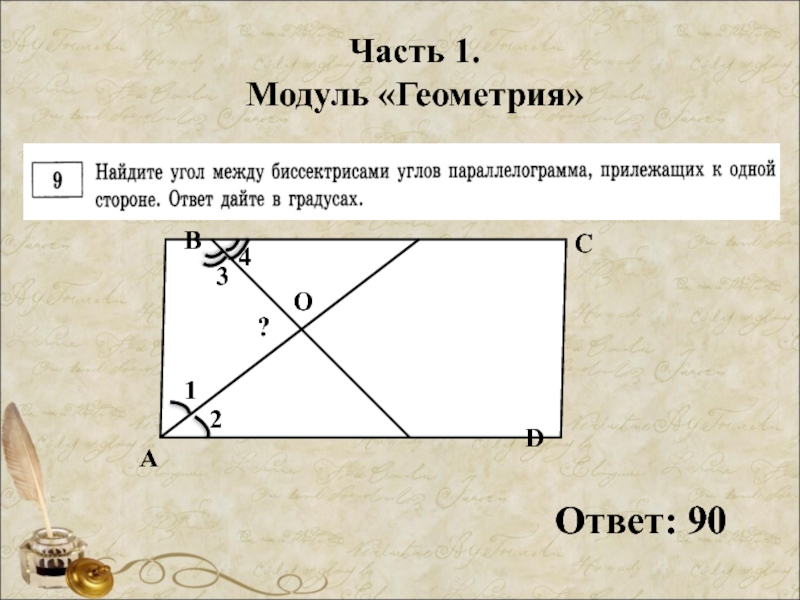
- 28. Часть 1. Модуль «Геометрия»
- 29. Часть 1. Модуль «Геометрия» Ответ: 90
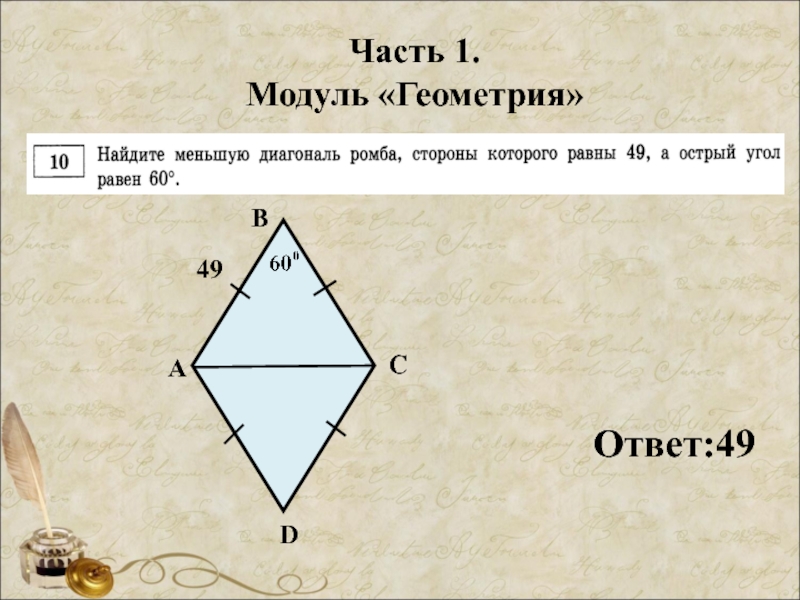
- 30. Часть 1. Модуль «Геометрия» Ответ:49 49 А В С D
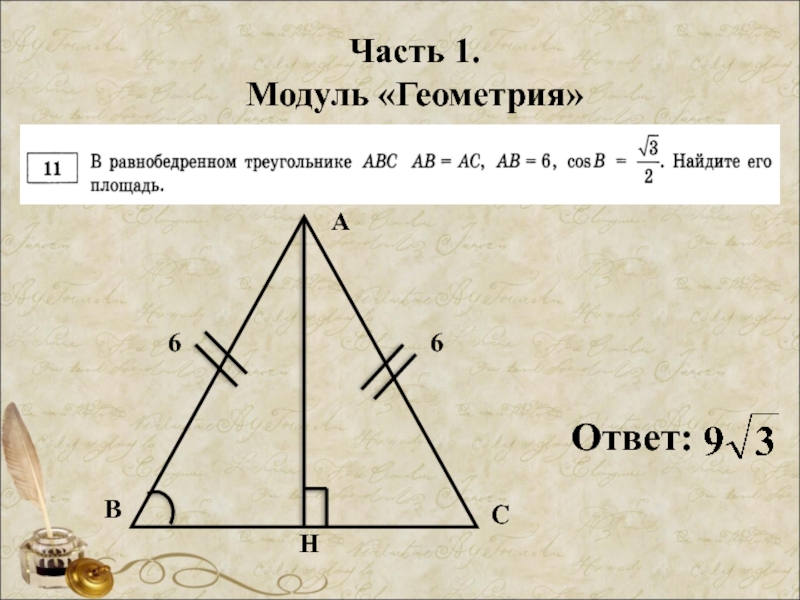
- 31. Часть 1. Модуль «Геометрия» Ответ: А В С Н 6 6
- 32. Часть 1. Модуль «Геометрия» Ответ: 0,25
- 33. 1 2 3 Если один из углов
- 34. Часть 1. Модуль «Реальная математика» Всего яиц:14+2+3+3+3=
- 35. Часть 1. Модуль «Реальная математика» Всего яиц:14+2+3+3+3=25
- 36. Часть 1. Модуль «Реальная математика» Всего яиц:14+2+3+3+3=25
- 37. Часть 1. Модуль «Реальная математика» Ответ: 3 Всего яиц:14+2+3+3+3=25
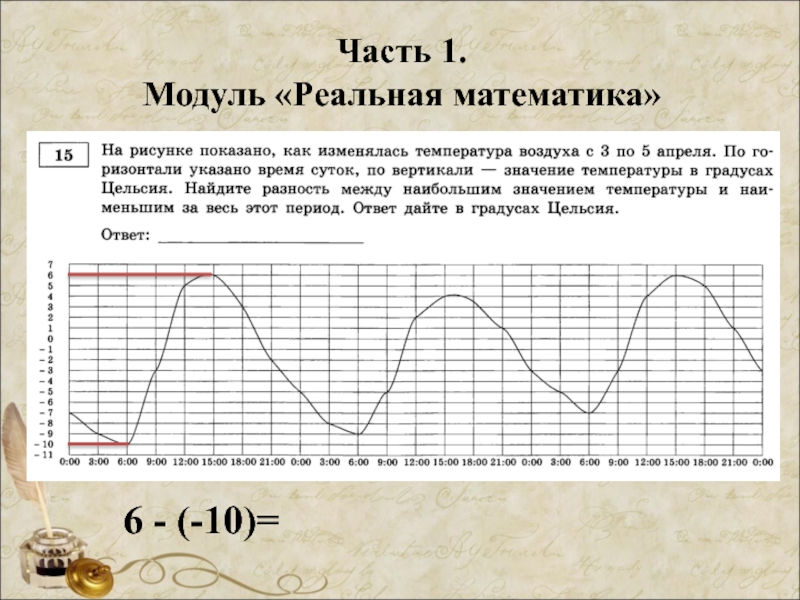
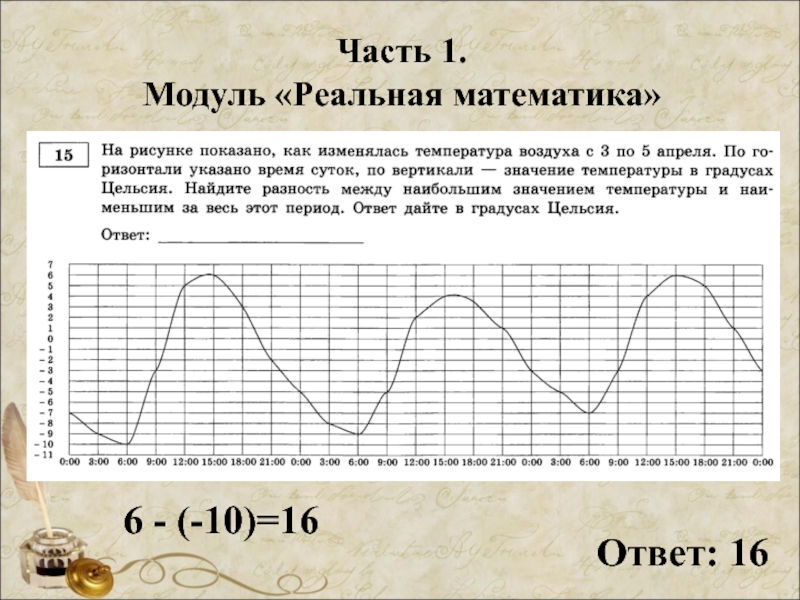
- 38. Часть 1. Модуль «Реальная математика» 6 - (-10)=
- 39. Часть 1. Модуль «Реальная математика» Ответ: 16 6 - (-10)=16
- 40. Часть 1. Модуль «Реальная математика» Ответ: 16
- 41. Часть 1. Модуль «Реальная математика»
- 42. Часть 1. Модуль «Реальная математика» ДОРОГА
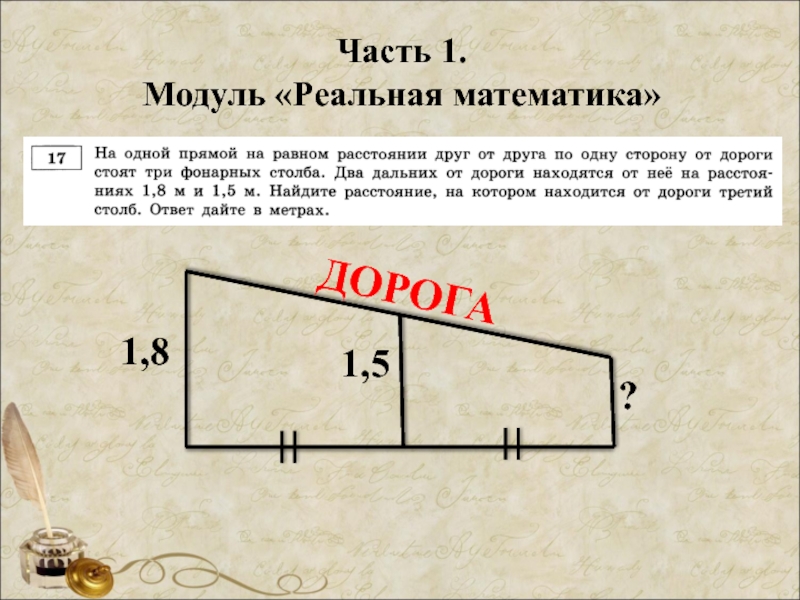
- 43. Часть 1. Модуль «Реальная математика» 1,8 1,5 ? ДОРОГА
- 44. Часть 1. Модуль «Реальная математика» 1,8 1,5 х Ответ: 1,2 ДОРОГА
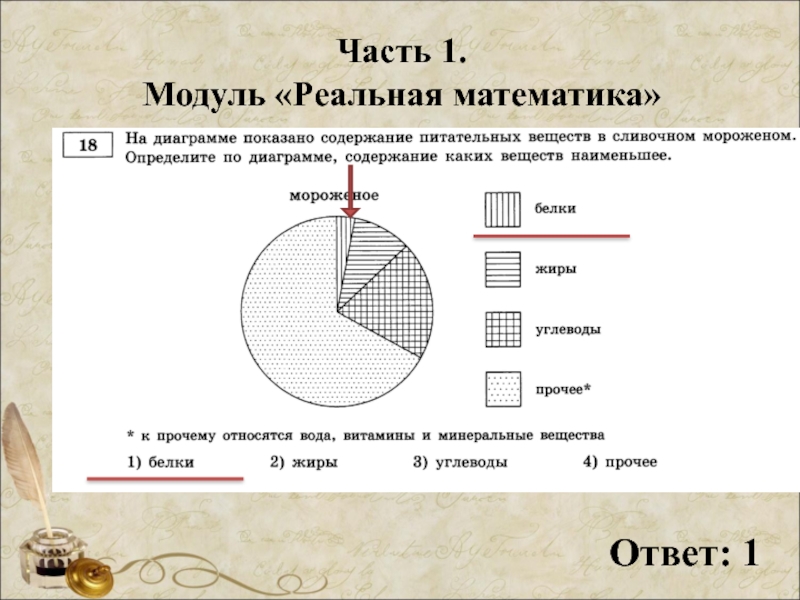
- 45. Часть 1. Модуль «Реальная математика» Ответ: 1
- 46. Часть 1. Модуль «Реальная математика»
- 47. Часть 1. Модуль «Реальная математика» Вероятность, что неисправны оба автомата:
- 48. Часть 1. Модуль «Реальная математика» Вероятность, что неисправны оба автомата: Р=0,05*0,05=
- 49. Часть 1. Модуль «Реальная математика» Вероятность, что неисправны оба автомата: Р=0,05*0,05=0,0025
- 50. Часть 1. Модуль «Реальная математика»
- 51. Часть 1. Модуль «Реальная математика»
- 52. Часть 1. Модуль «Реальная математика»
- 53. Часть 1. Модуль «Реальная математика» S = 330*19 =
- 54. Часть 1. Модуль «Реальная математика» S = 330*19 = 6270
- 55. Часть 1. Модуль «Реальная математика» S = 330*19 = 6270 м
- 56. Часть 1. Модуль «Реальная математика»
- 57. Часть 1. Модуль «Реальная математика»
- 58. Домашнее задание: Вариант – 16.
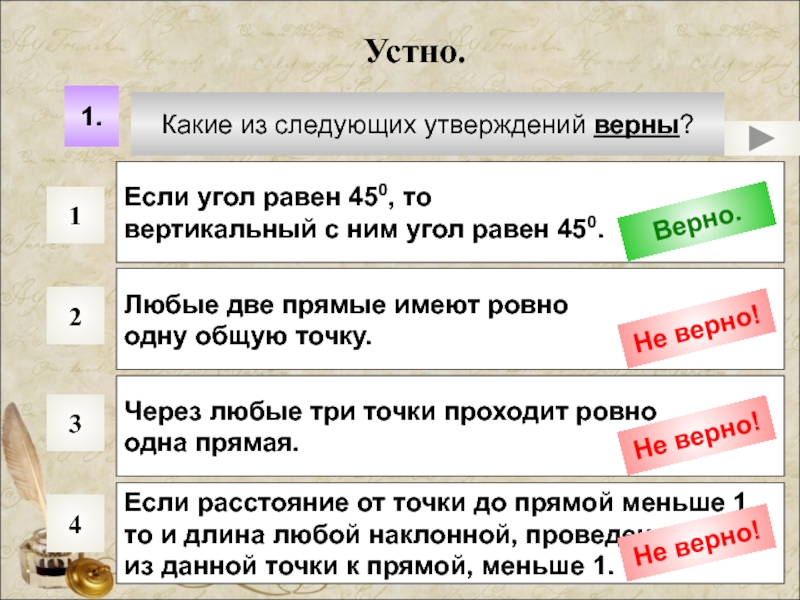
Слайд 2Какие из следующих утверждений верны?
1
2
3
4
Если угол равен 450, то
вертикальный
Любые две прямые имеют ровно
одну общую точку.
Через любые три точки проходит ровно
одна прямая.
Если расстояние от точки до прямой меньше 1,
то и длина любой наклонной, проведенной
из данной точки к прямой, меньше 1.
Верно.
Не верно!
Не верно!
Не верно!
1.
Устно.
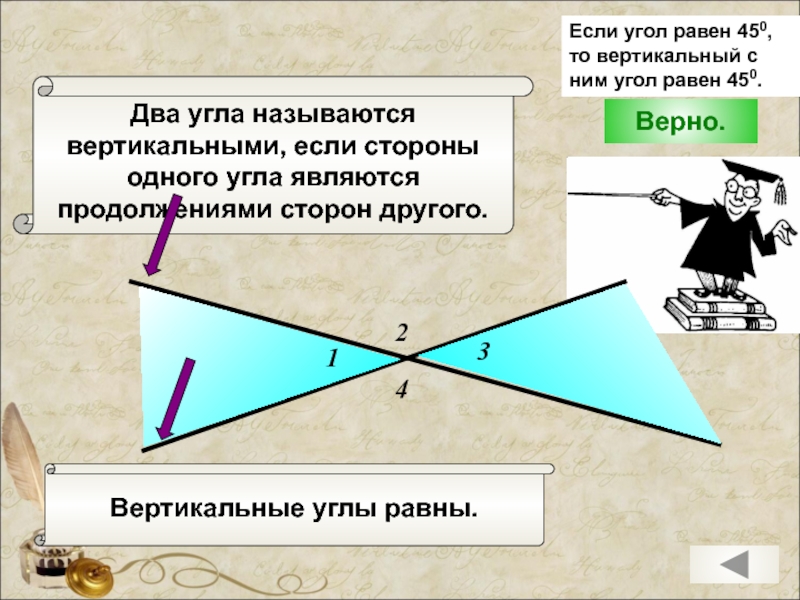
Слайд 3Два угла называются
вертикальными, если стороны
одного угла являются
продолжениями сторон другого.
2
4
1
3
Вертикальные углы
Если угол равен 450, то вертикальный с ним угол равен 450.
Верно.
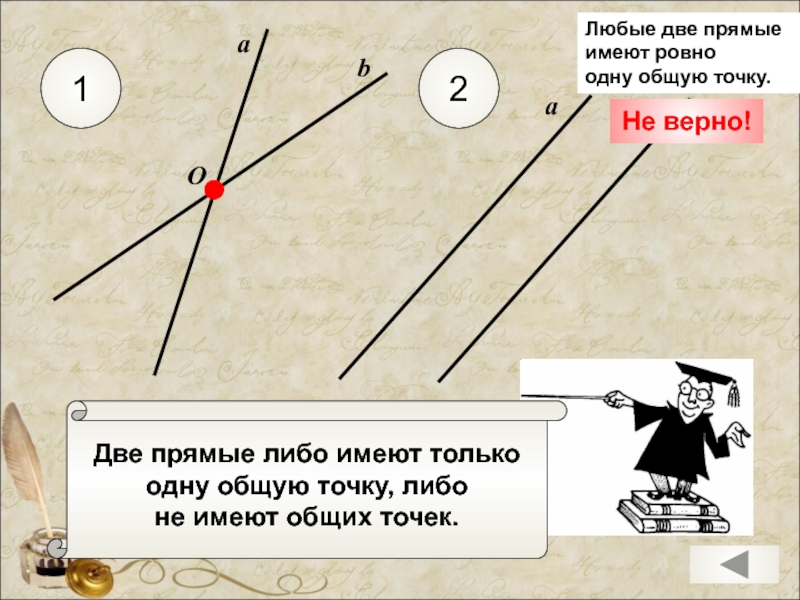
Слайд 4
Две прямые либо имеют только
одну общую точку, либо
не имеют общих точек.
1
2
b
O
а
b
а
Любые
одну общую точку.
Не верно!
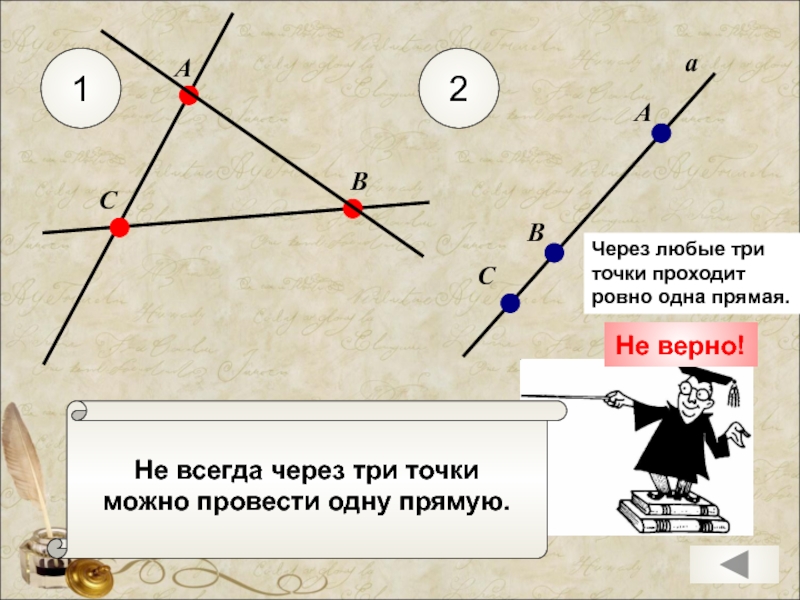
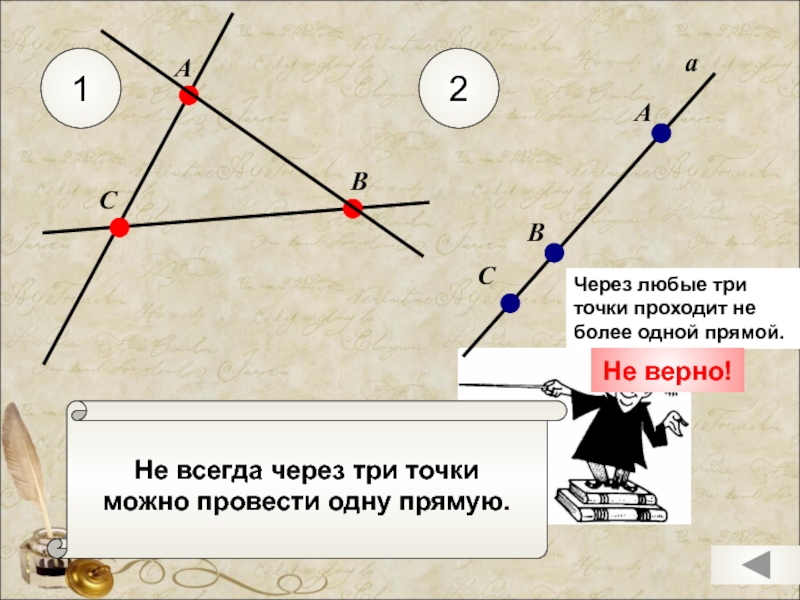
Слайд 5
Не всегда через три точки
можно провести одну прямую.
1
2
С
А
В
а
А
В
С
Через любые три точки
Не верно!
Слайд 6
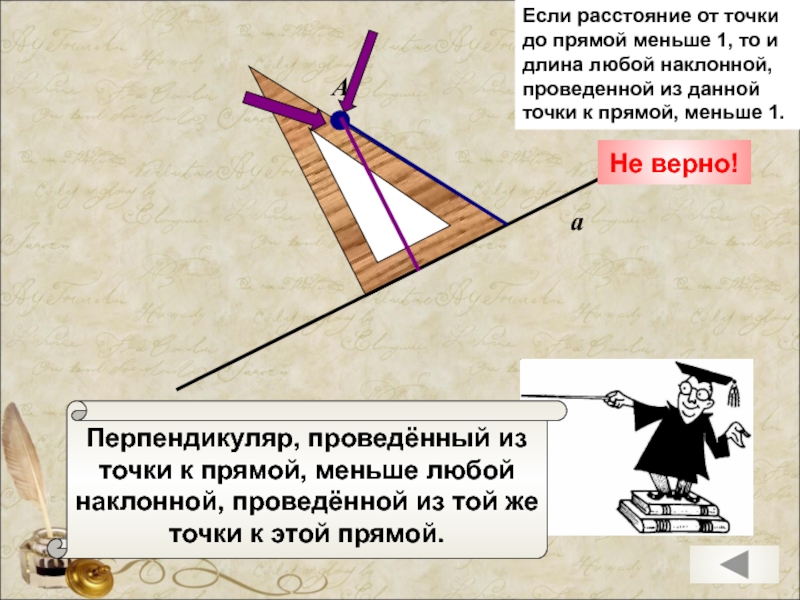
Перпендикуляр, проведённый из
точки к прямой, меньше любой
наклонной, проведённой из той же
точки
а
А
Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
Не верно!
Слайд 7Какие из следующих утверждений верны?
1
2
3
4
Если при пересечении двух прямых секущей
внутренние накрест лежащие углы составляют
в сумме 900, то эти две прямые параллельны.
Если угол равен 600, то смежный
с ним угол равен 1200.
Если при пересечении двух прямых секущей
внутренние односторонние углы равны
600 и 1100, то эти две прямые параллельны.
Через любые три точки проходит
не более одной прямой.
Не верно!
Верно.
Не верно!
Не верно!
2.
Устно.
Слайд 8
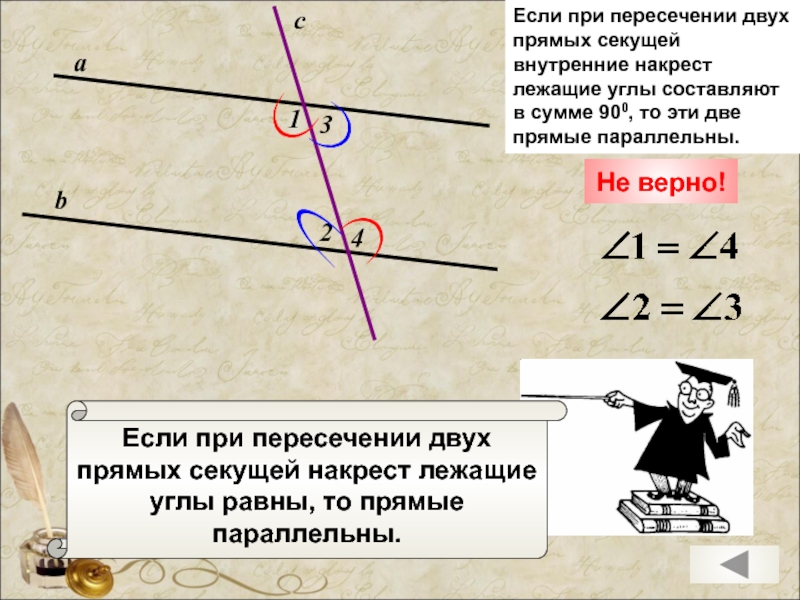
Если при пересечении двух
прямых секущей накрест лежащие
углы равны, то
параллельны.
а
b
c
1
2
3
4
Если при пересечении двух прямых секущей внутренние накрест лежащие углы составляют в сумме 900, то эти две прямые параллельны.
Не верно!
Слайд 9
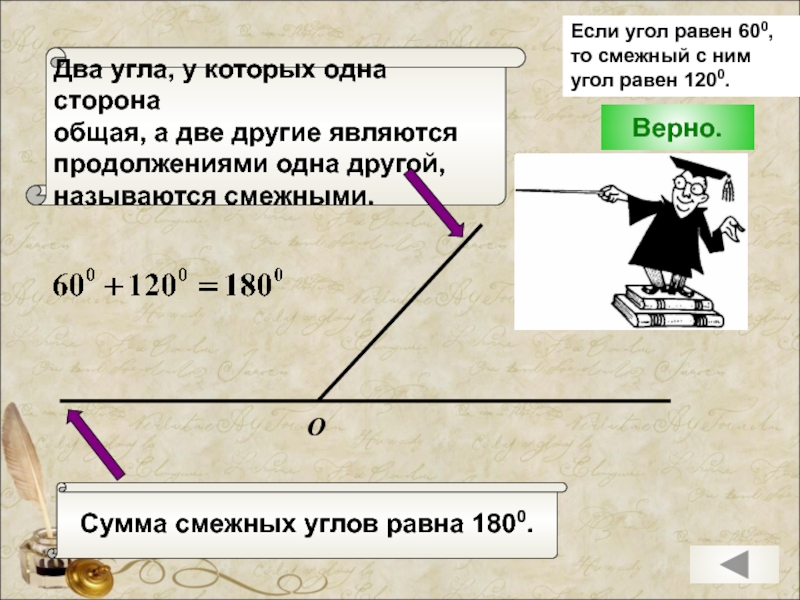
Сумма смежных углов равна 1800.
Два угла, у которых одна сторона
общая, а
продолжениями одна другой,
называются смежными.
О
Если угол равен 600, то смежный с ним угол равен 1200.
Верно.
Слайд 10
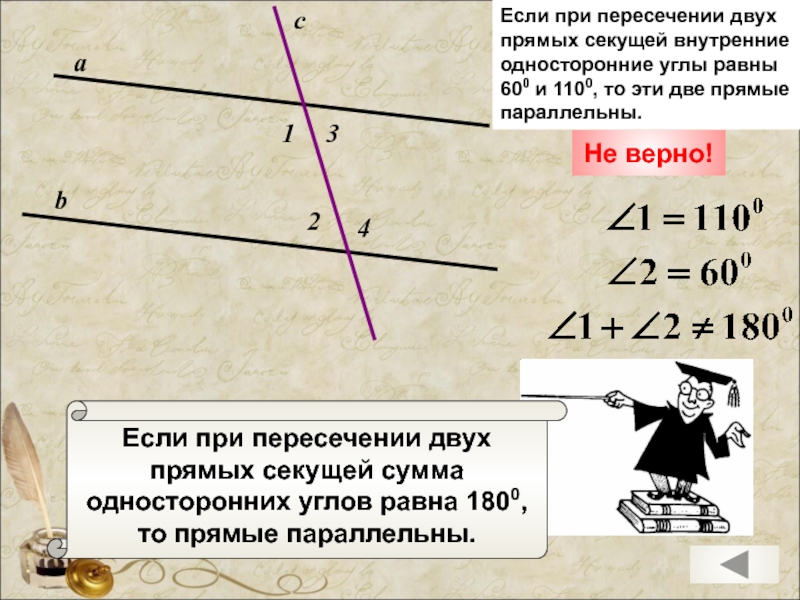
Если при пересечении двух
прямых секущей сумма
односторонних углов равна 1800,
то прямые параллельны.
а
b
c
1
2
3
4
Если при пересечении двух прямых секущей внутренние односторонние углы равны
600 и 1100, то эти две прямые параллельны.
Не верно!
Слайд 11
Не всегда через три точки
можно провести одну прямую.
1
2
С
А
В
а
А
В
С
Через любые три точки
Не верно!
Слайд 12Какие из следующих утверждений верны?
3.
1
2
3
4
Если расстояние между центрами двух
окружностей
то эти окружности касаются.
Вписанные углы окружности равны.
Если вписанный угол равен 300, то дуга
окружности, на которую опирается этот угол,
равна 600.
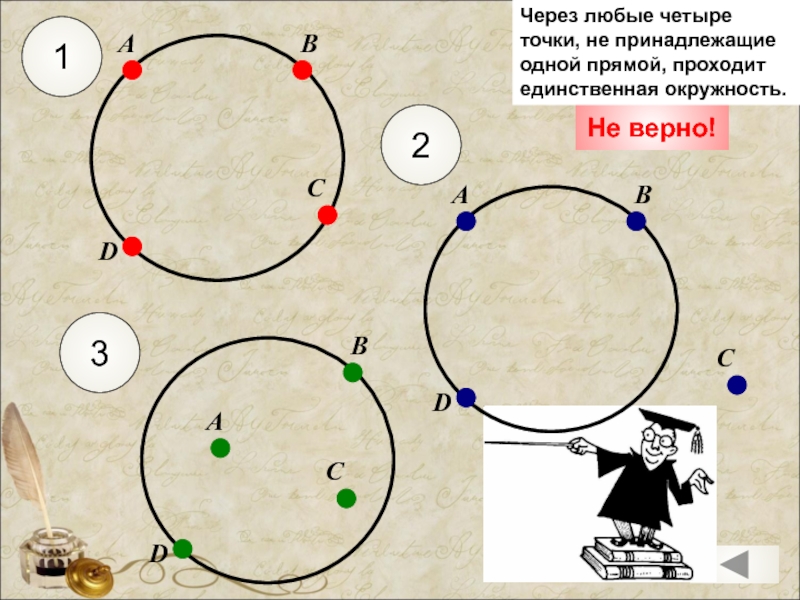
Через любые четыре точки, не принадлежащие
одной прямой, проходит единственная
окружность.
Не верно!
Не верно!
Верно.
Не верно!
Устно.
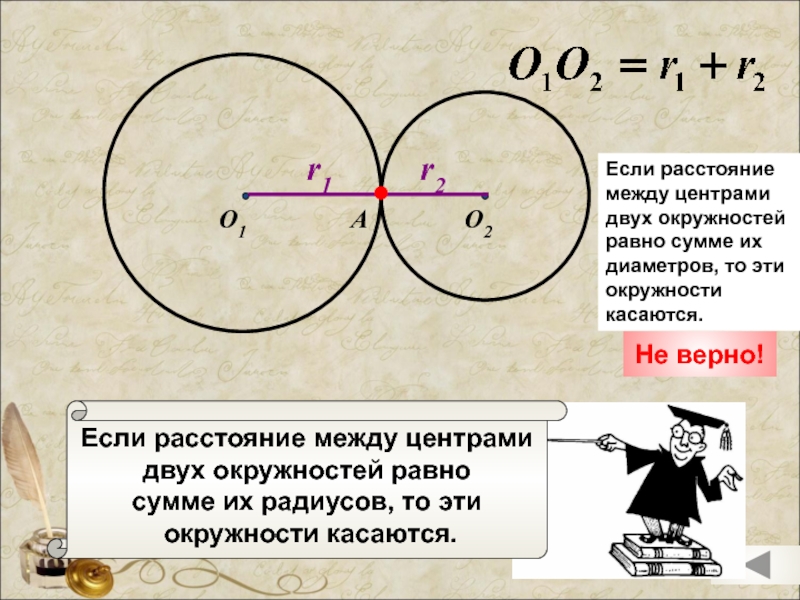
Слайд 13
Если расстояние между центрами
двух окружностей равно
сумме их радиусов, то
окружности касаются.
О1
О2
r1
r2
А
Не верно!
Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.
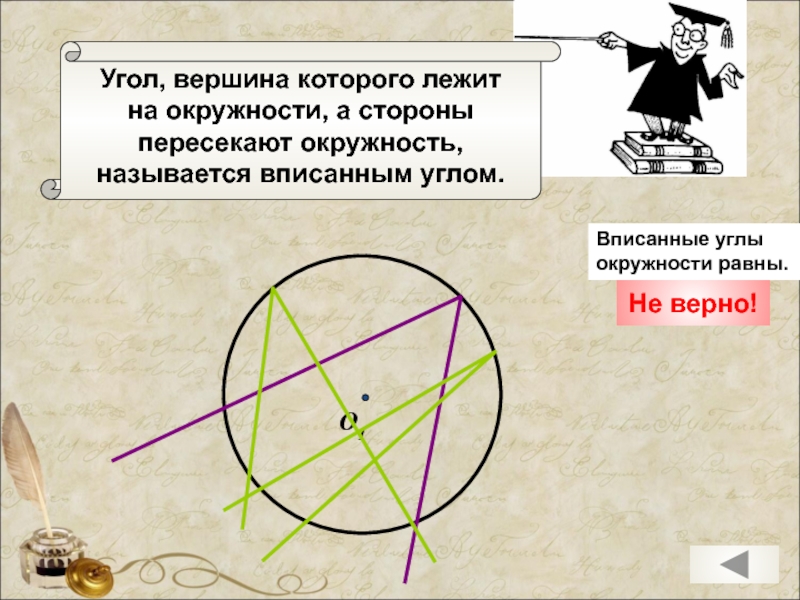
Слайд 14
Угол, вершина которого лежит
на окружности, а стороны
пересекают окружность,
называется вписанным углом.
О1
Не
Вписанные углы окружности равны.
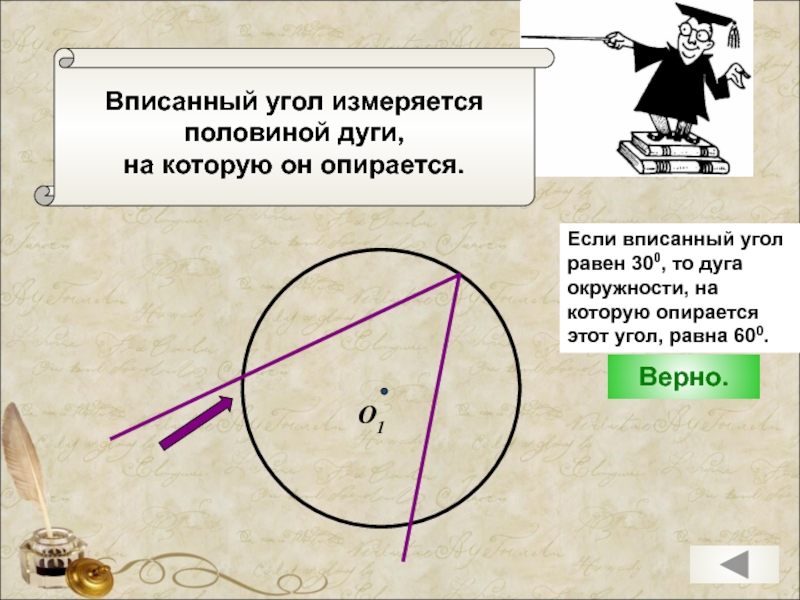
Слайд 15
Вписанный угол измеряется
половиной дуги,
на которую он опирается.
О1
Верно.
Если вписанный угол равен 300,
окружности, на которую опирается этот угол, равна 600.
Слайд 16
1
С
А
В
D
2
С
А
В
D
С
А
В
D
3
Не верно!
Через любые четыре точки, не принадлежащие
одной прямой, проходит единственная
Слайд 331
2
3
Если один из углов треугольника равен 300,
то другой его угол
Если три стороны одного треугольника соответ-
ственно в 5 раз больше трёх сторон другого
треугольника, то такие треугольники подобны.
Сумма углов прямоугольного треугольника
равна 1800.
Не верно!
Верно.
Часть 1.
Модуль «Геометрия»
Верно.
Ответ: 23
Слайд 40Часть 1.
Модуль «Реальная математика»
Ответ: 16
1200 р. – 100%
1392 р. – х%
1200
192 р. – х%
или
Слайд 49Часть 1.
Модуль «Реальная математика»
Вероятность, что неисправны оба автомата: Р=0,05*0,05=0,0025
Слайд 50Часть 1.
Модуль «Реальная математика»
Вероятность, что неисправны оба автомата: Р=0,05*0,05=0,0025
Вероятность, что исправен
Слайд 51Часть 1.
Модуль «Реальная математика»
Вероятность, что неисправны оба автомата: Р=0,05*0,05=0,0025
Вероятность, что исправен
Слайд 52Часть 1.
Модуль «Реальная математика»
Вероятность, что неисправны оба автомата: Р=0,05*0,05=0,0025
Вероятность, что исправен
Ответ: 0,9975












![Часть 1.Модуль «Алгебра»Ответ: х Є (-∞; -1,25]](/img/tmb/5/453632/57704a063408c31ee0716d5ac80a5862-800x.jpg)