- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ЕГЭ. Задание В7 презентация
Содержание
- 1. Подготовка к ЕГЭ. Задание В7
- 2. В7 Умения выполнять действия с функциями (геометрический и физический смысл производной)
- 3. -9 -8 -7 -6 -5 -
- 4. -9 -8 -7 -6 -5
- 5. -9 -8 -7 -6 -5
- 6. 4. Непрерывная функция у
- 7. 5. Непрерывная функция у = f(x)
- 8. 6. Непрерывная функция
- 9. 7. На рисунке изображен график производной
- 10. y = f /(x)
- 11. y = f /(x)
- 12. y = f /(x)
- 13. 11. На рисунке изображены график
- 14. 12. На рисунке изображены график
- 15. 13. На рисунке
- 16. 14. На рисунке изображен график функции
- 17. 15. На рисунке изображен график y=f'(x) —
- 18. 16. На рисунке изображен график
- 19. 17. На рисунке изображен график
- 20. 18. На рисунке изображен график y=f'(x) —
- 21. 19. На рисунке изображен график y=f'(x) —
- 22. 20. На рисунке изображен график y=f’(x)
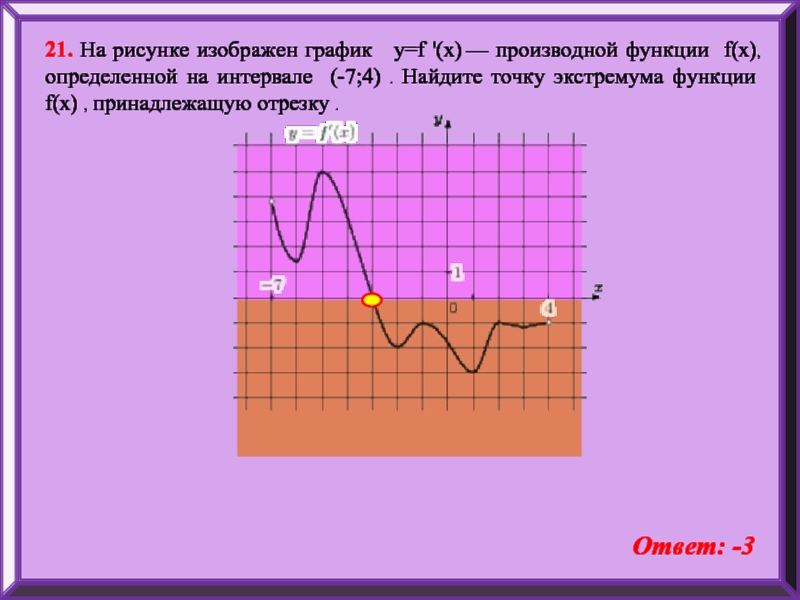
- 23. 21. На рисунке изображен график y=f
- 24. На рисунке изображены график функции y=f(x)
- 25. На рисунке изображен график функции y=f(x) ,
- 26. Материал с открытого банка заданий mathege.ru
Слайд 3 -9 -8 -7 -6 -5 - 4 -3 -2
1 2 3 4 5 6 7 8
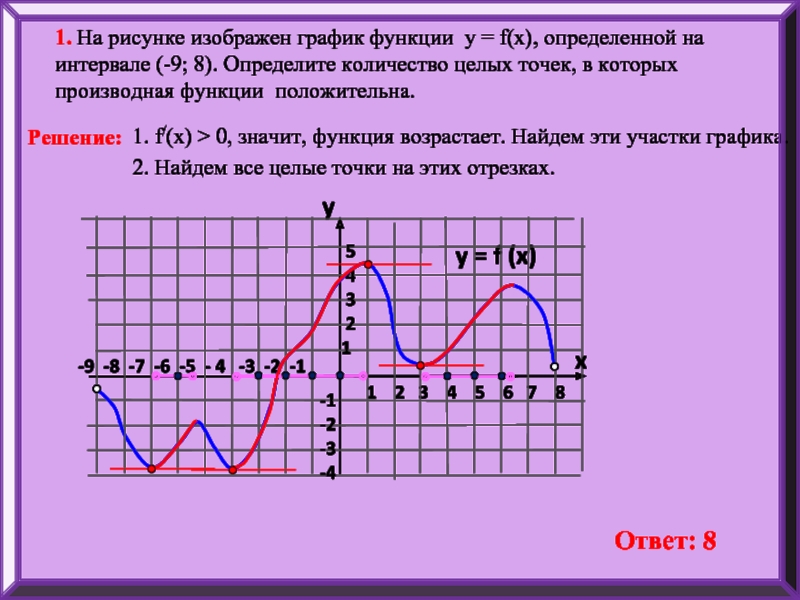
1. На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:
Слайд 4 -9 -8 -7 -6 -5 - 4 -3 -2
1 2 3 4 5 6 7 8
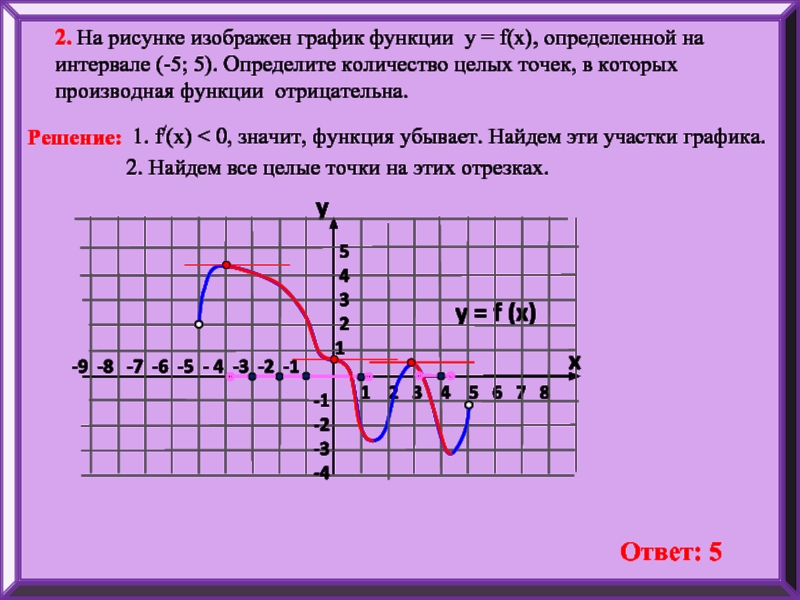
2. На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 5
Решение:
Слайд 5 -9 -8 -7 -6 -5 - 4 -3 -2
1 2 3 4 5 6 7 8
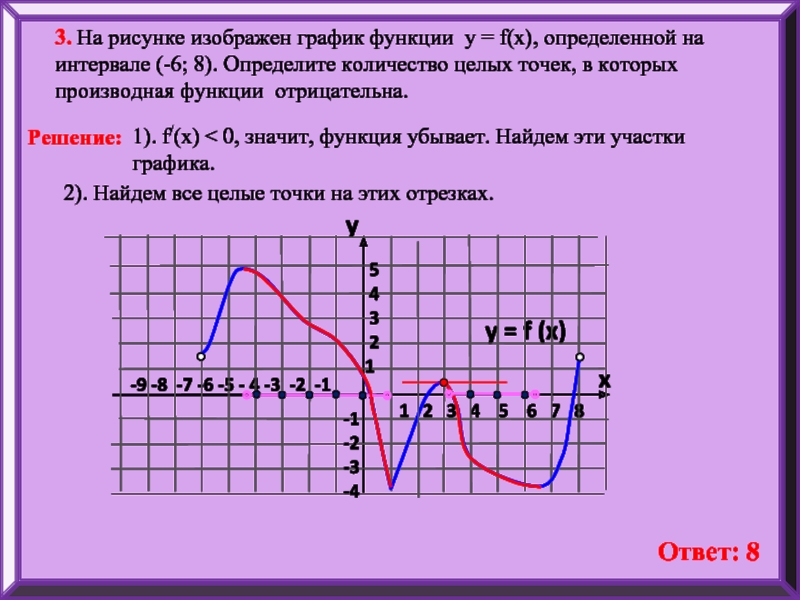
3. На рисунке изображен график функции у = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции отрицательна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1). f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2). Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:
Слайд 6
4. Непрерывная функция у = f(x) задана на отрезке
На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
y = f(x)
y
x
Ответ: 5
a
b
Слайд 7
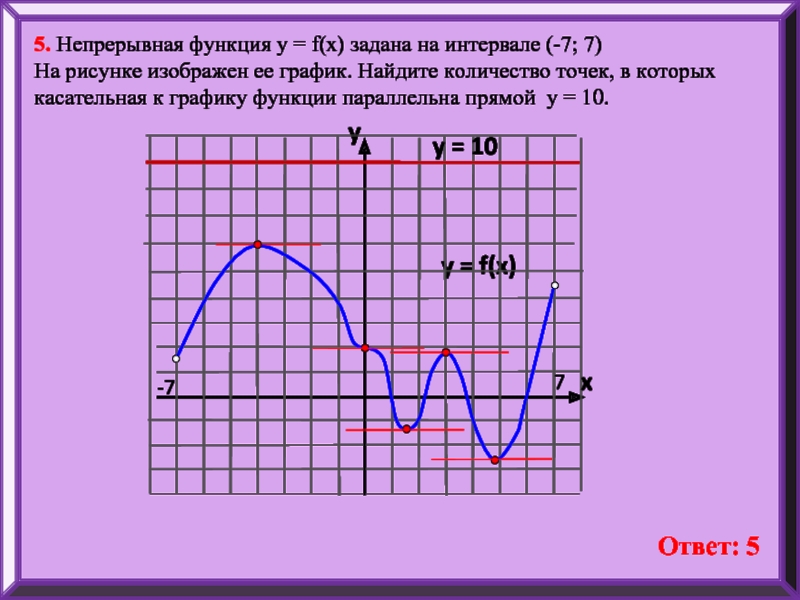
5. Непрерывная функция у = f(x) задана на интервале (-7; 7)
На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 10.
y = f(x)
y
x
-7
7
Ответ: 5
Слайд 8
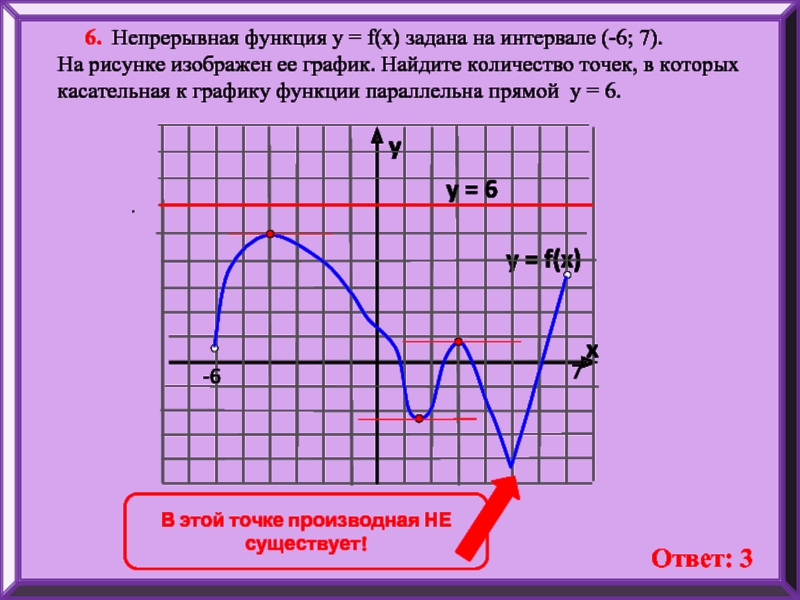
6. Непрерывная функция у = f(x) задана на
На рисунке изображен ее график. Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6.
y = f(x)
y
x
-6
7
.
В этой точке производная НЕ существует!
Ответ: 3
Слайд 9
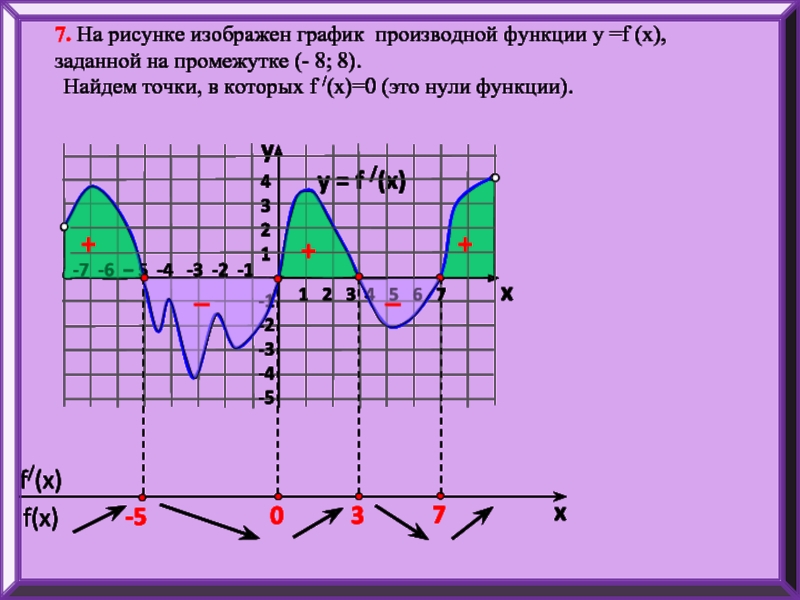
7. На рисунке изображен график производной функции у =f (x), заданной
y = f /(x)
1 2 3 4 5 6 7
-7 -6 – 5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+
Слайд 10
y = f /(x)
1 2 3 4 5
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
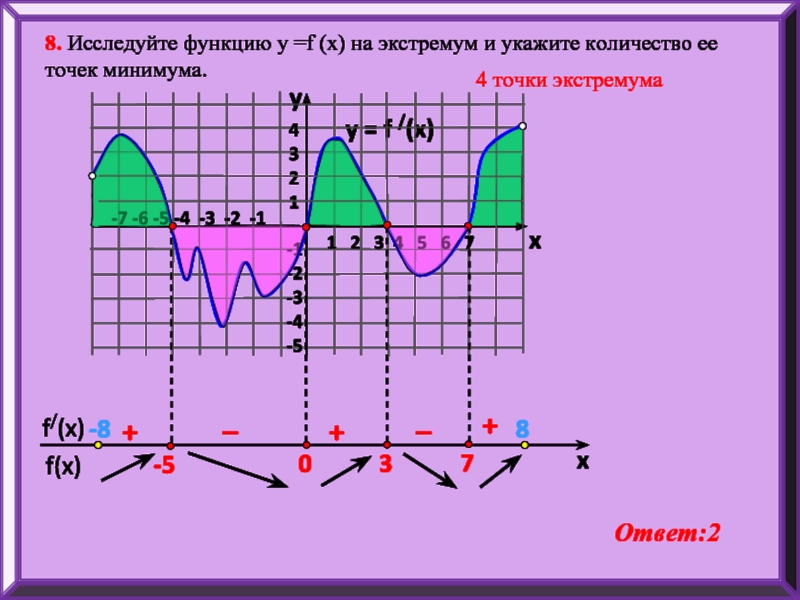
8. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума
Ответ:2
-8
8
Слайд 11
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
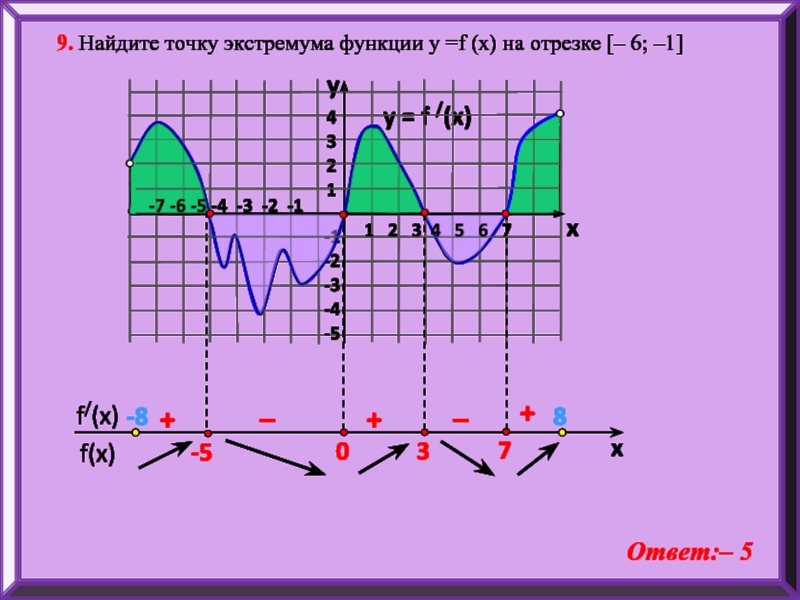
9. Найдите точку экстремума функции у =f (x)
Ответ:– 5
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-8
8
Слайд 12
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
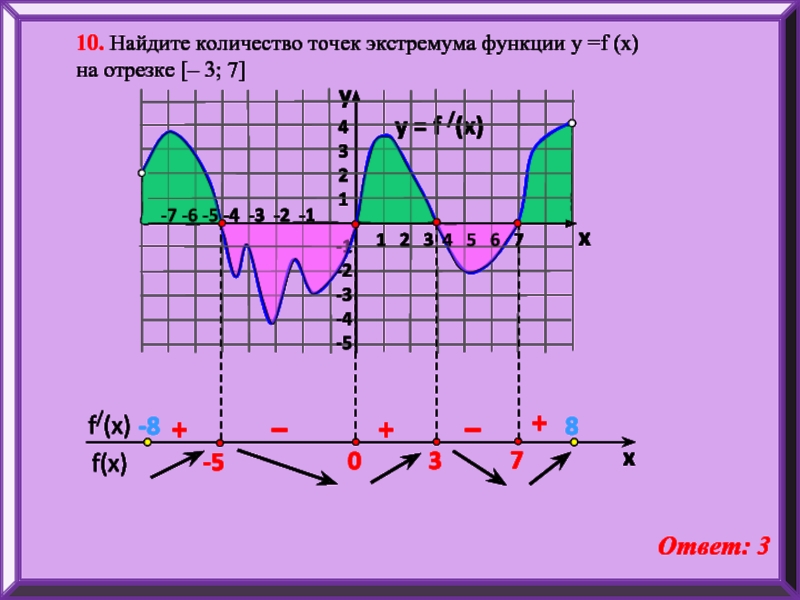
10. Найдите количество точек экстремума функции у =f
на отрезке [– 3; 7]
Ответ: 3
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-8
8
Слайд 13
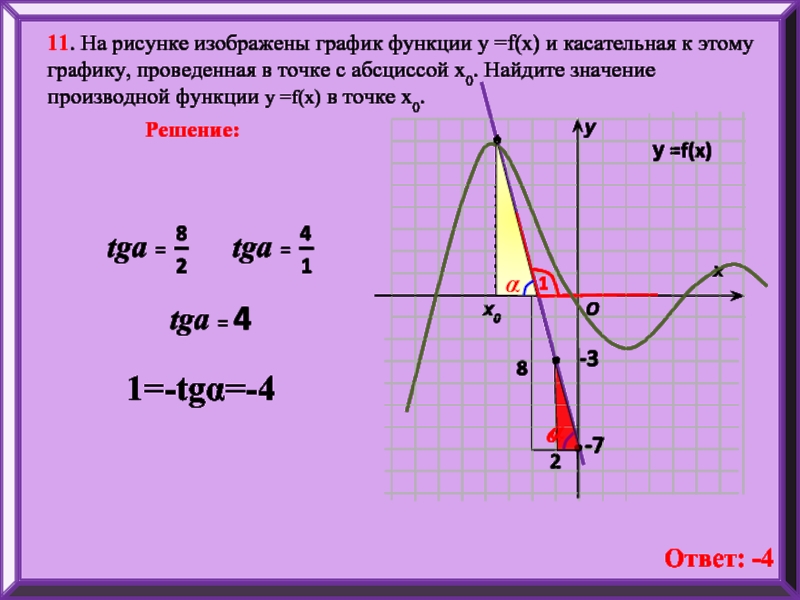
11. На рисунке изображены график функции у =f(x) и касательная к
х
х0
у
Решение:
O
у =f(x)
-3
-7
1=-tgα=-4
Ответ: -4
Слайд 14
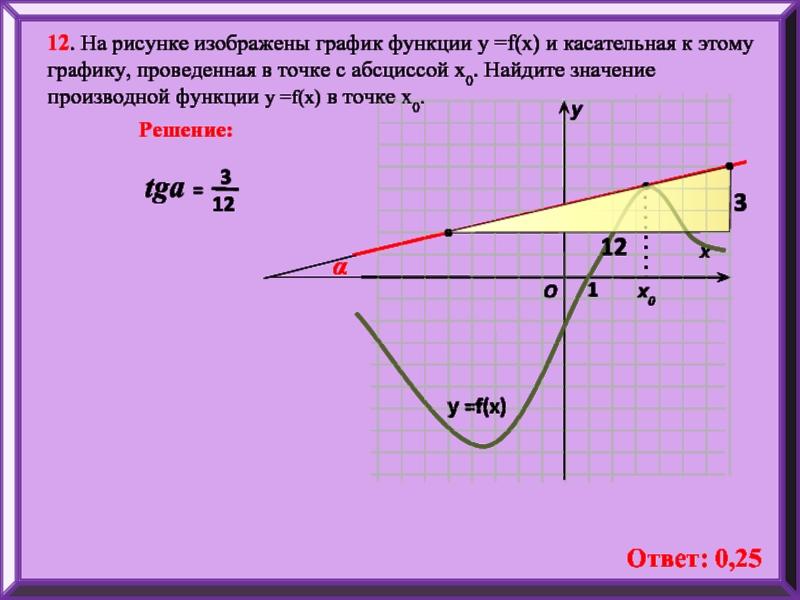
12. На рисунке изображены график функции у =f(x) и касательная к
х
х0
у
Решение:
O
у =f(x)
1
α
Ответ: 0,25
Слайд 15
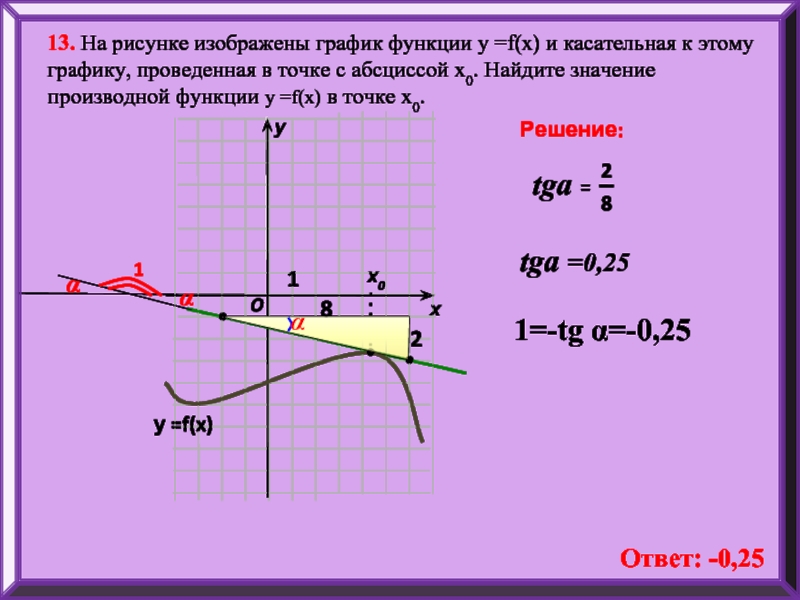
13. На рисунке изображены график функции у =f(x) и касательная к
х
х0
у
Решение:
O
у =f(x)
1
α
α
Ответ: -0,25
tga =0,25
1=-tg α=-0,25
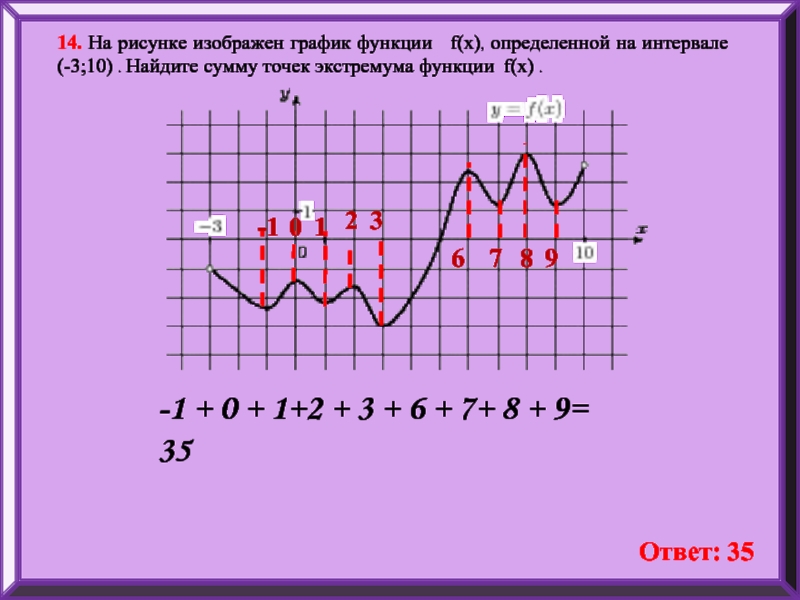
Слайд 1614. На рисунке изображен график функции f(x), определенной на интервале
-1
0
1
3
6
7
8
9
-1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35
Ответ: 35
2
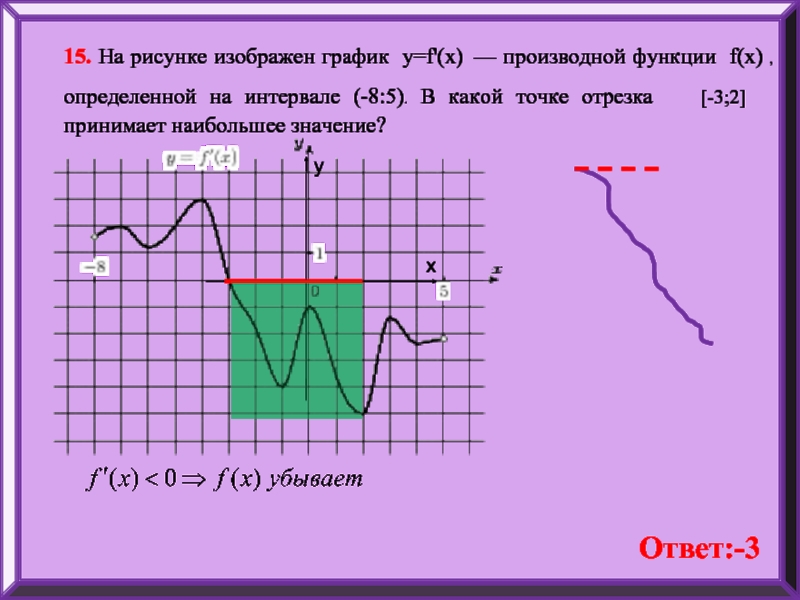
Слайд 1715. На рисунке изображен график y=f'(x) — производной функции f(x) ,
Ответ:-3
Слайд 18
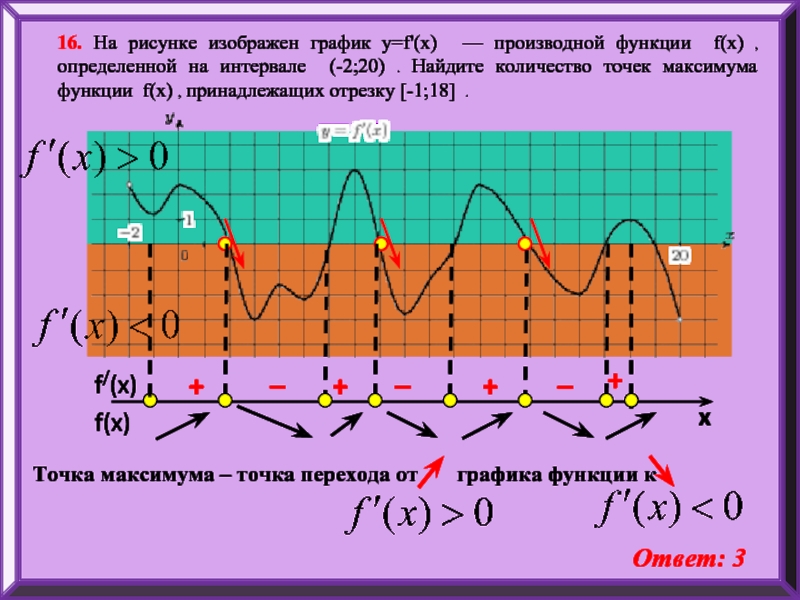
16. На рисунке изображен график y=f'(x) — производной функции f(x) ,
Ответ: 3
_
–
–
+
+
+
+
Слайд 19
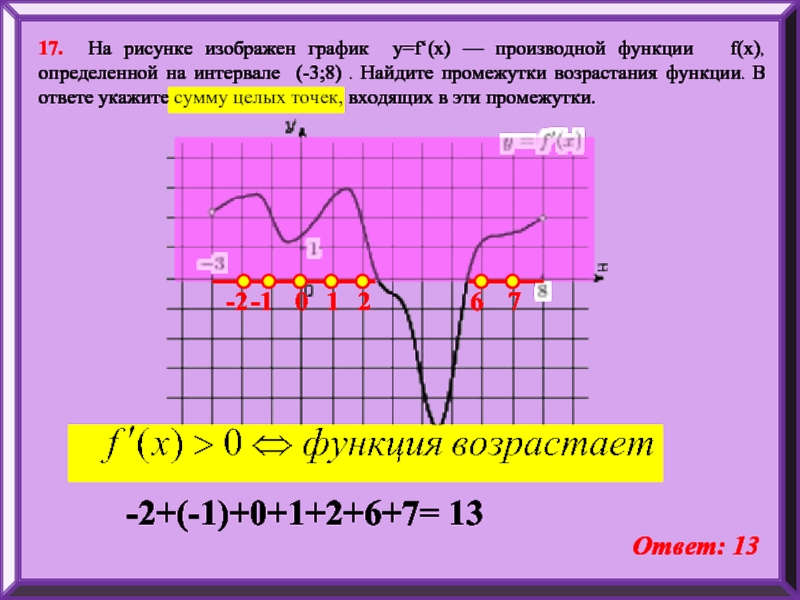
17. На рисунке изображен график y=f‘(x) — производной функции f(x),
-2
-1
0
1
2
6
7
-2+(-1)+0+1+2+6+7= 13
Ответ: 13
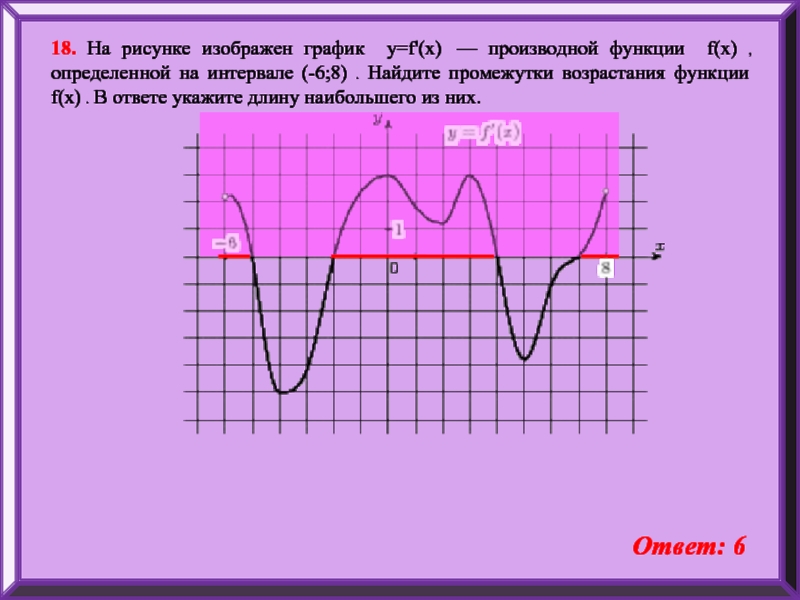
Слайд 2018. На рисунке изображен график y=f'(x) — производной функции f(x) ,
Ответ: 6
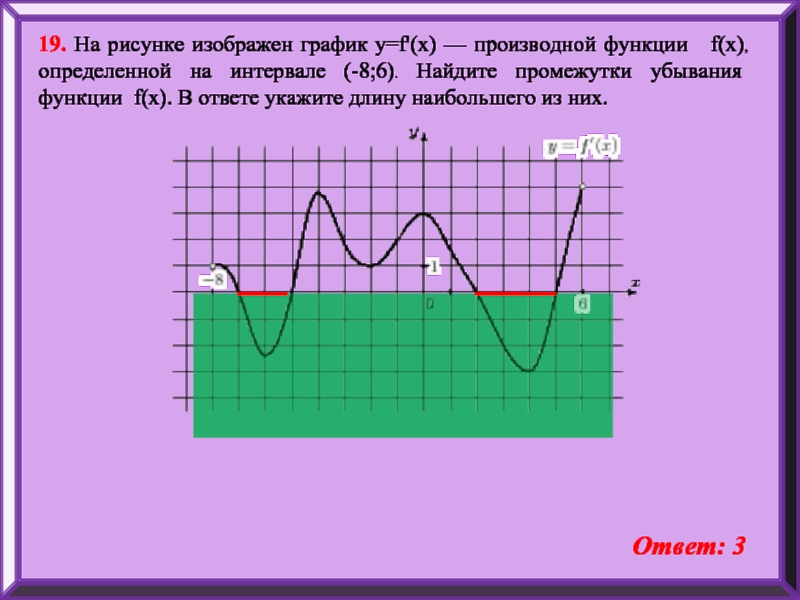
Слайд 2119. На рисунке изображен график y=f'(x) — производной функции f(x),
Ответ: 3
Слайд 22
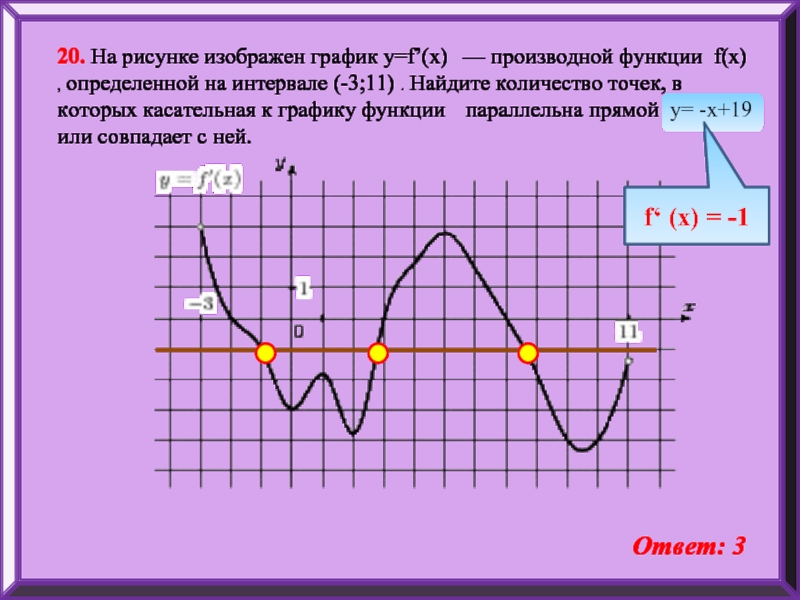
20. На рисунке изображен график y=f’(x) — производной функции f(x) ,
f‘ (x) = -1
Ответ: 3
Слайд 2321. На рисунке изображен график y=f '(x) — производной функции f(x),
Ответ: -3
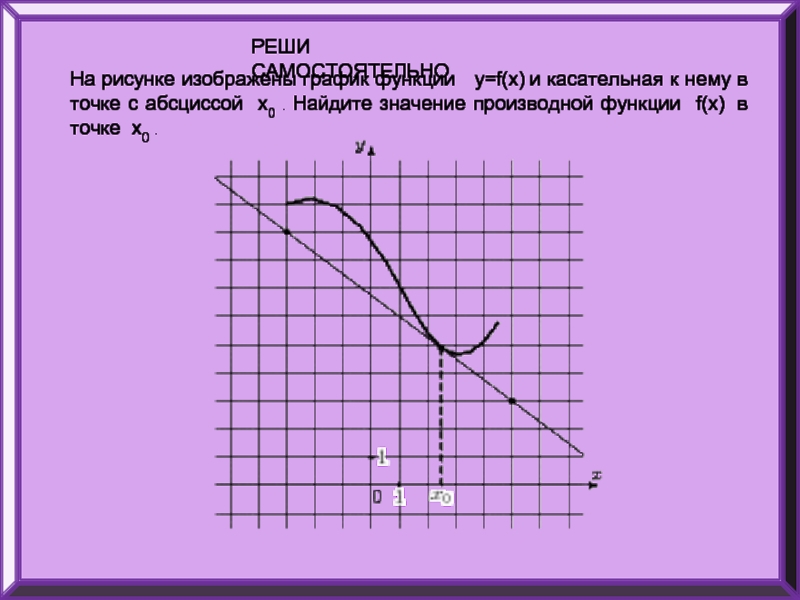
Слайд 24На рисунке изображены график функции y=f(x) и касательная к нему
РЕШИ САМОСТОЯТЕЛЬНО
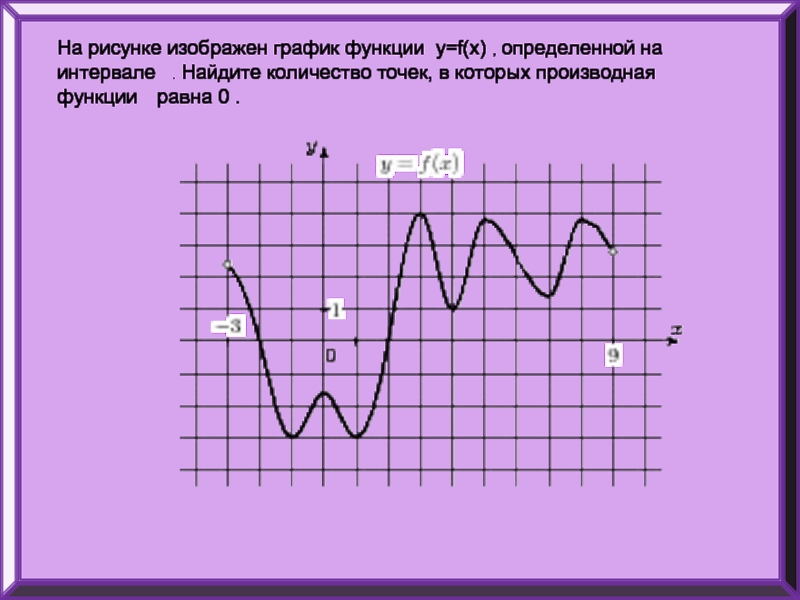
Слайд 25На рисунке изображен график функции y=f(x) , определенной на интервале
