- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подібні трикутники. (8 клас) презентация
Содержание
- 1. Подібні трикутники. (8 клас)
- 2. Подібні трикутники Два трикутники називаються подібними, якщо
- 3. Подібні трикутники Щоб скласти відношення відповідних сторін
- 4. Узагальнена теорема Фалеса (теорема про пропорційні відрізки).
- 5. Щоб довести подібність трикутників: Доведіть рівність відповідних
- 6. Ознаки подібності трикутників Геометрія 8 клас
- 7. Перша ознака подібності трикутників Теорема (ознака
- 8. Ознаки подібності трикутників Щоб довести подібність двох
- 9. Наслідки: Рівносторонні трикутники подібні. Рівнобедрені трикутники подібні,
- 10. Друга ознака подібності трикутників Теорема (ознака подібності
- 11. Третя ознака подібності трикутників Теорема (ознака подібності
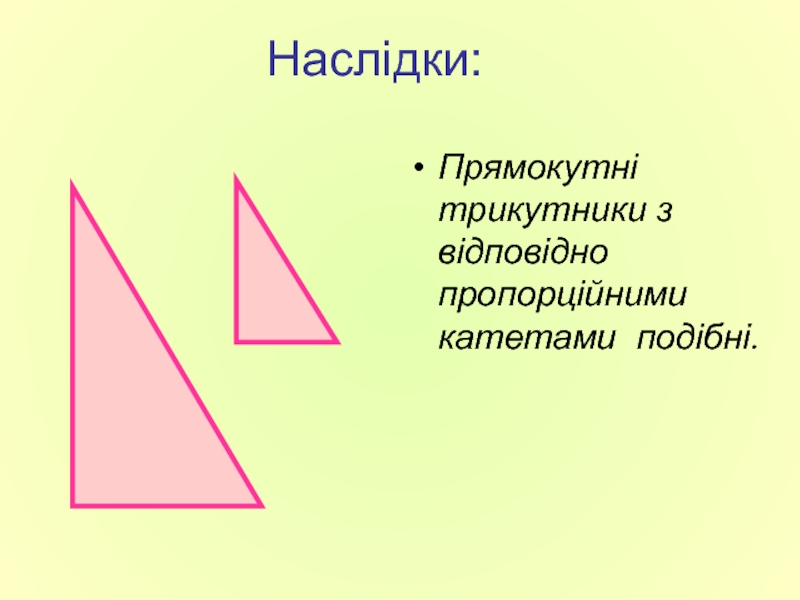
- 12. Наслідки: Прямокутні трикутники з відповідно пропорційними катетами подібні.
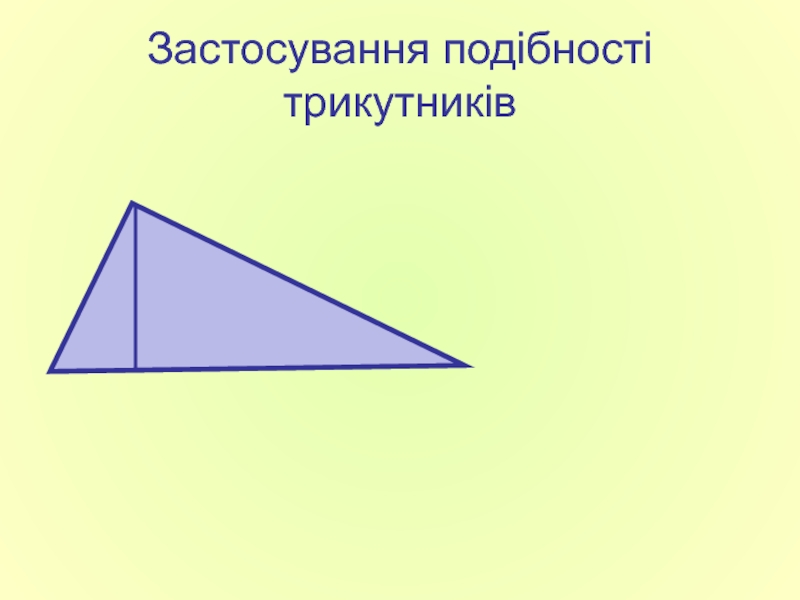
- 13. Застосування подібності трикутників
- 14. Теорема (про середні пропорційні у прямокутному відрізку)
- 15. Властивість бісектриси трикутника Бісектриса трикутника ділить
- 16. Волошина Валентина Іванівна Вчитель
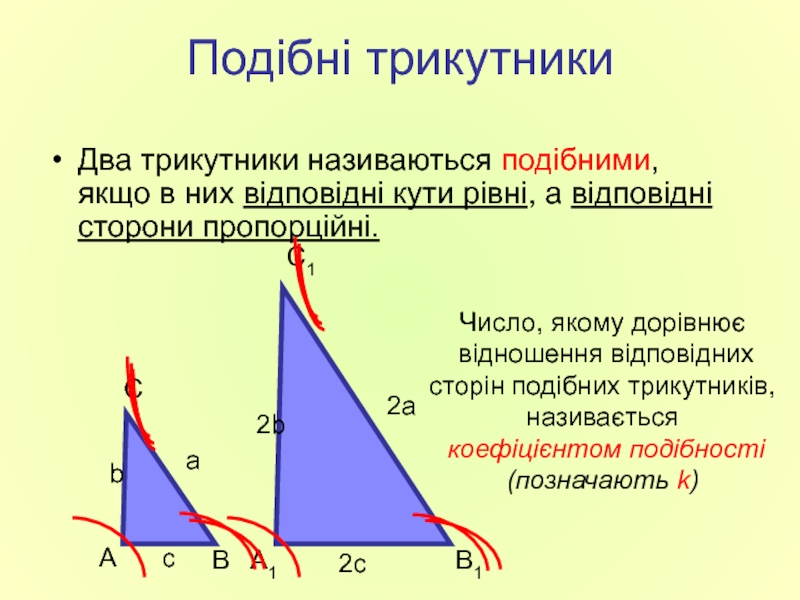
Слайд 2Подібні трикутники
Два трикутники називаються подібними, якщо в них відповідні кути рівні,
А
С
В
А1
С1
В1
b
2b
a
2a
c
2c
Число, якому дорівнює
відношення відповідних
сторін подібних трикутників,
називається
коефіцієнтом подібності
(позначають k)
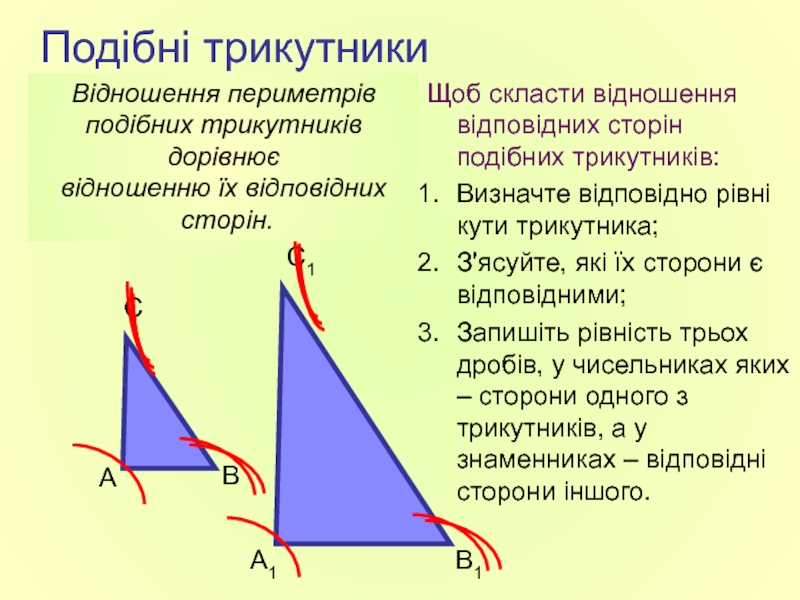
Слайд 3Подібні трикутники
Щоб скласти відношення відповідних сторін подібних трикутників:
Визначте відповідно рівні кути
З'ясуйте, які їх сторони є відповідними;
Запишіть рівність трьох дробів, у чисельниках яких – сторони одного з трикутників, а у знаменниках – відповідні сторони іншого.
А
С
В
А1
С1
В1
Відношення периметрів
подібних трикутників дорівнює
відношенню їх відповідних
сторін.
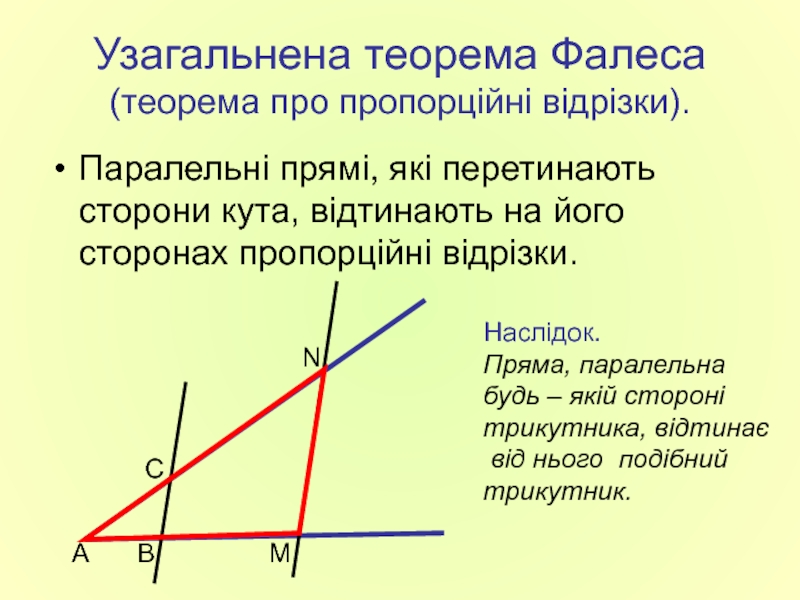
Слайд 4Узагальнена теорема Фалеса
(теорема про пропорційні відрізки).
Паралельні прямі, які перетинають сторони кута,
А
В
М
N
С
Наслідок.
Пряма, паралельна
будь – якій стороні
трикутника, відтинає
від нього подібний
трикутник.
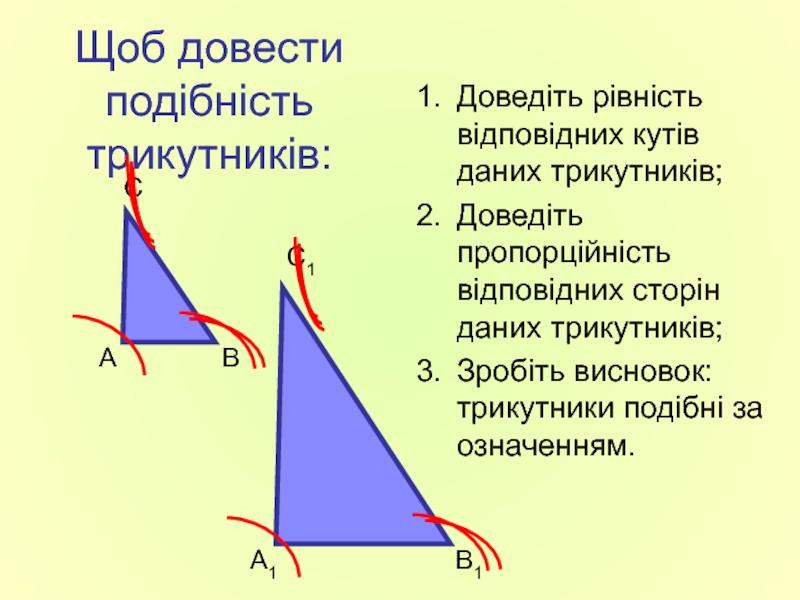
Слайд 5Щоб довести подібність трикутників:
Доведіть рівність відповідних кутів даних трикутників;
Доведіть пропорційність відповідних
Зробіть висновок: трикутники подібні за означенням.
А
С
В
А1
С1
В1
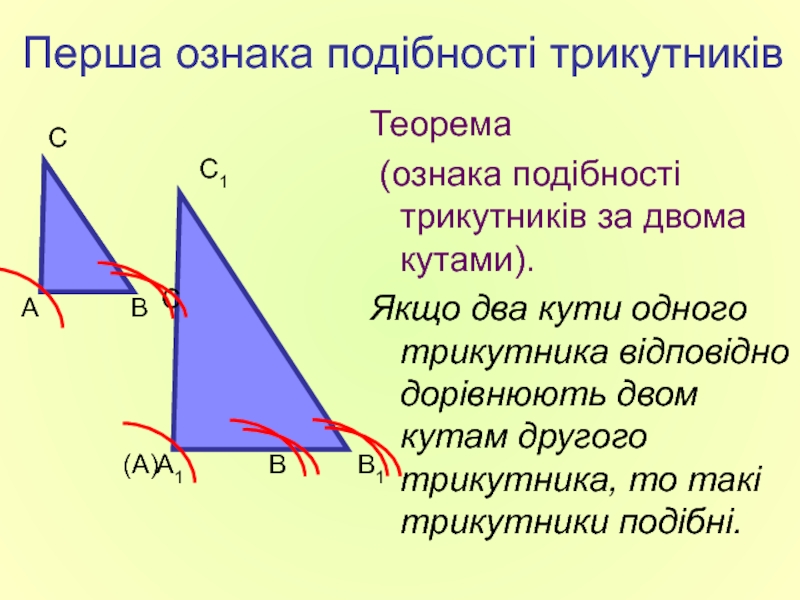
Слайд 7Перша ознака подібності трикутників
Теорема
(ознака подібності трикутників за двома кутами).
Якщо два
А
В
С
А1
В1
С1
С
В
(А)
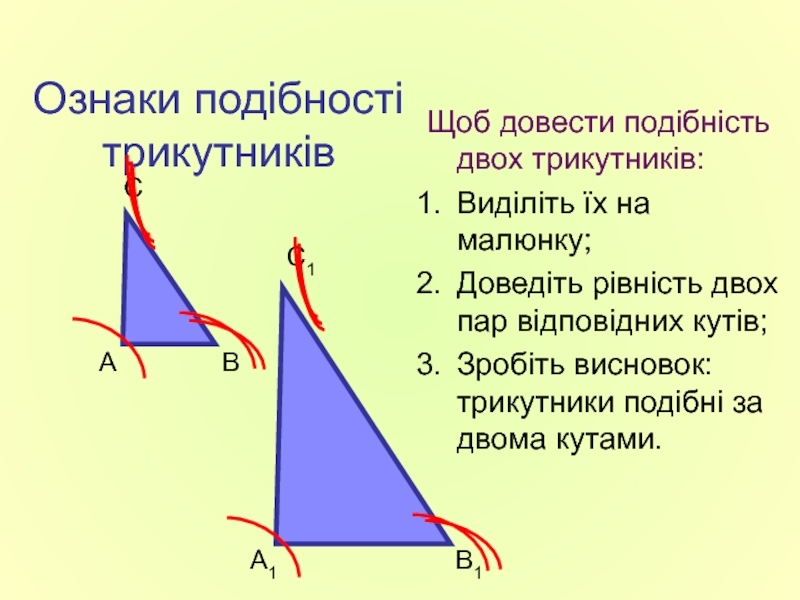
Слайд 8Ознаки подібності трикутників
Щоб довести подібність двох трикутників:
Виділіть їх на малюнку;
Доведіть рівність
Зробіть висновок: трикутники подібні за двома кутами.
А
С
В
А1
С1
В1
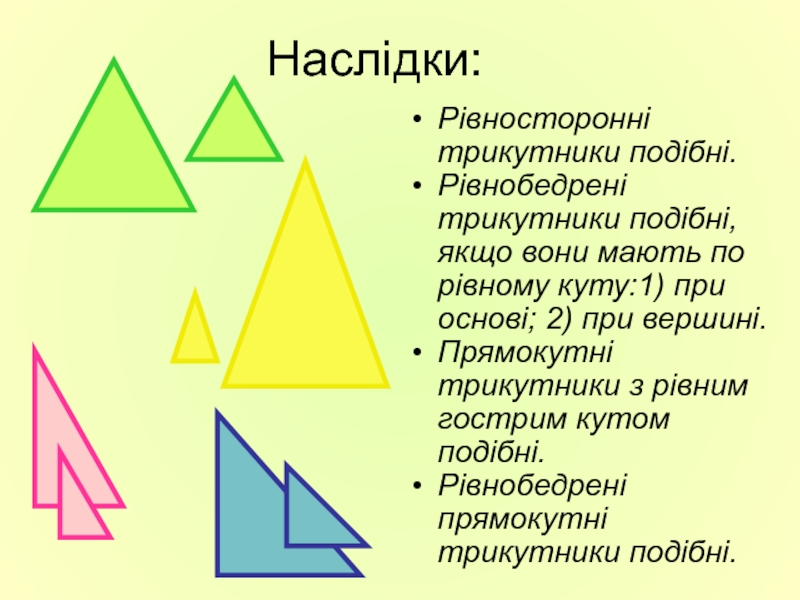
Слайд 9Наслідки:
Рівносторонні трикутники подібні.
Рівнобедрені трикутники подібні, якщо вони мають по рівному куту:1)
Прямокутні трикутники з рівним гострим кутом подібні.
Рівнобедрені прямокутні трикутники подібні.
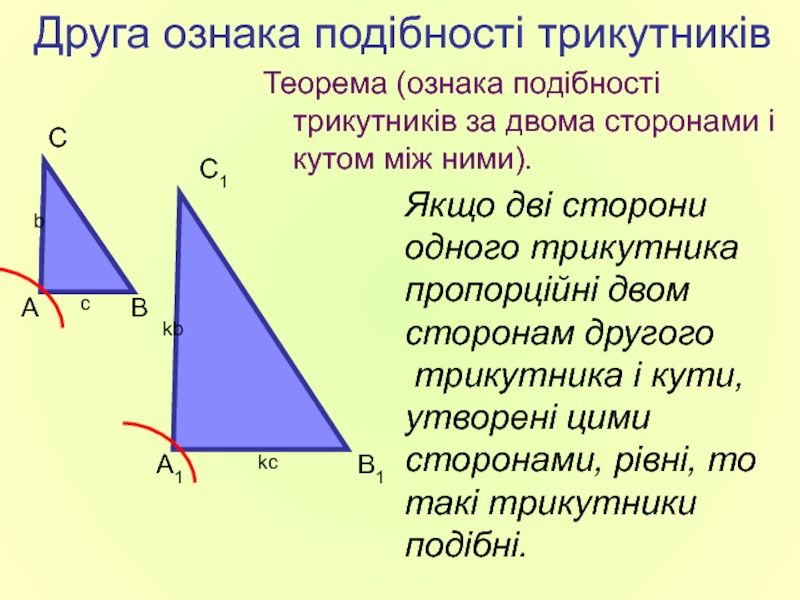
Слайд 10Друга ознака подібності трикутників
Теорема (ознака подібності трикутників за двома сторонами і
А
В
С
А1
В1
С1
Якщо дві сторони одного трикутника пропорційні двом сторонам другого
трикутника і кути,
утворені цими сторонами, рівні, то такі трикутники подібні.
c
kc
kb
b
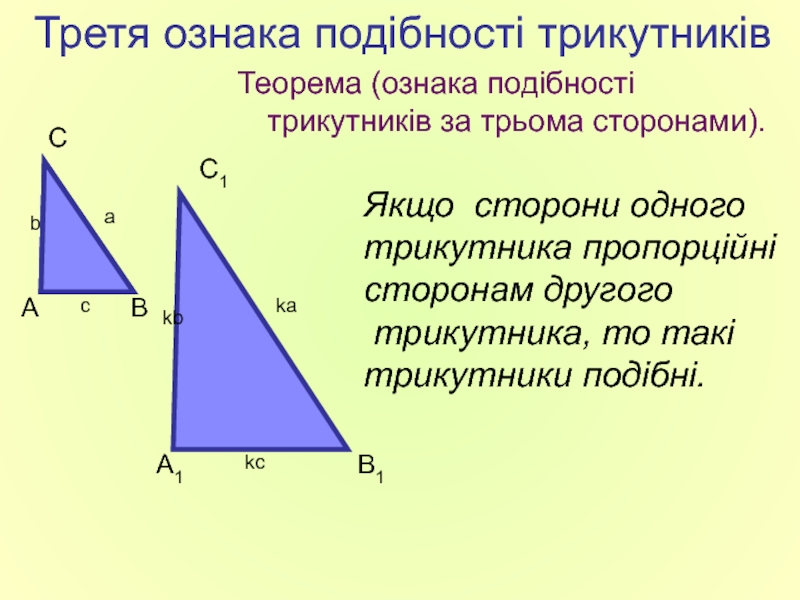
Слайд 11Третя ознака подібності трикутників
Теорема (ознака подібності трикутників за трьома сторонами).
А
В
С
А1
В1
С1
Якщо сторони
трикутника, то такі трикутники подібні.
b
a
c
kb
ka
kc
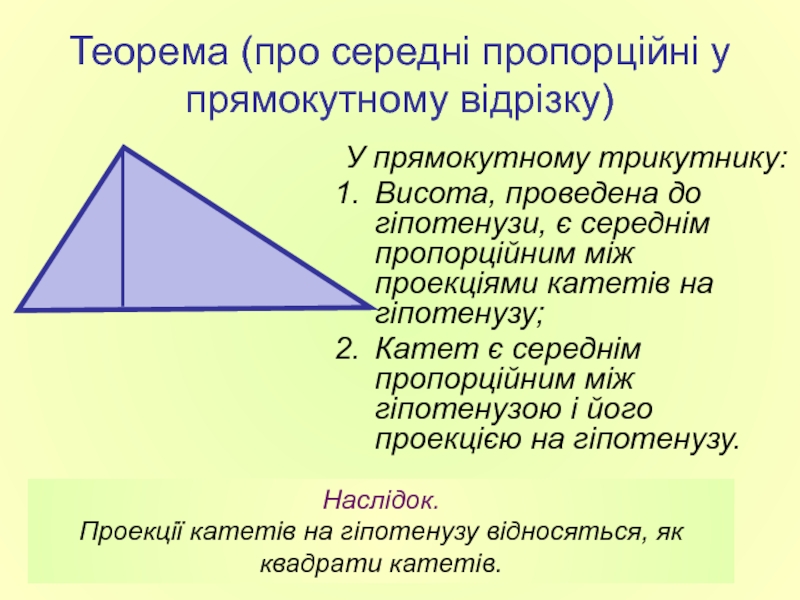
Слайд 14Теорема (про середні пропорційні у прямокутному відрізку)
У прямокутному трикутнику:
Висота, проведена до
Катет є середнім пропорційним між гіпотенузою і його проекцією на гіпотенузу.
Наслідок.
Проекції катетів на гіпотенузу відносяться, як квадрати катетів.
Слайд 15
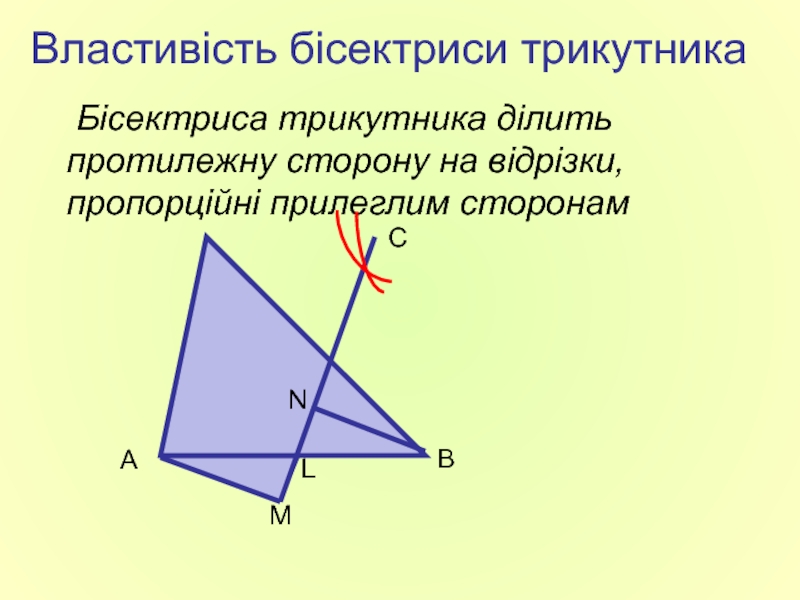
Властивість бісектриси трикутника
Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим
А
В
С
М
L
N
Слайд 16
Волошина Валентина Іванівна
Вчитель математики
Вчитель-методист
Вчитель вищої категорії
Спеціалізована школа № 7 ім. М.
м. Києва
2010 рік