- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Побудова перерізів многогранників презентация
Содержание
- 1. Побудова перерізів многогранників
- 2. Мета: Повторити геометричні поняття і твердження; навчитися
- 3. Геометричні поняття; Геометричні твердження; Основні поняття; Побудови перерізів;
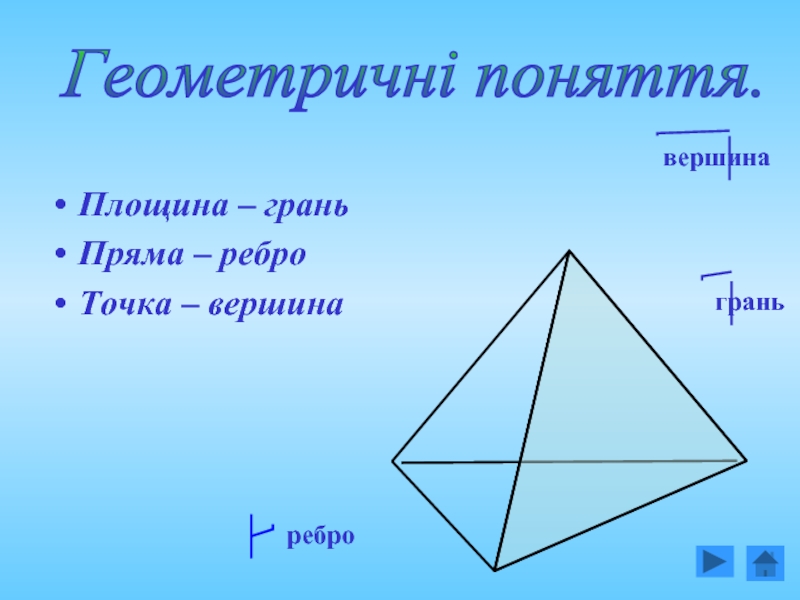
- 4. грань ребро вершина Геометричні поняття.
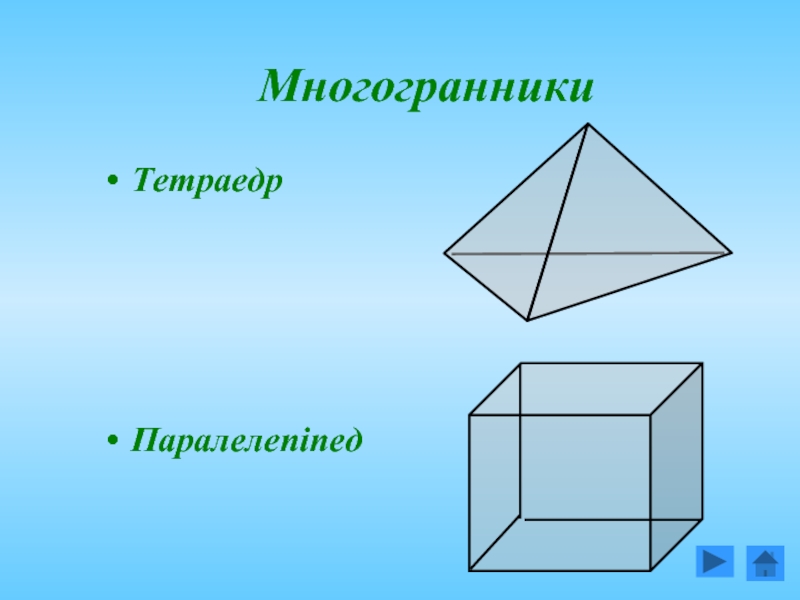
- 5. Многогранники Тетраедр Паралелепіпед
- 6. Геометричні твердження. Якщо дві
- 7. Геометричні твердження. Якщо дві
- 8. Січною площиною многогранника називається така площина
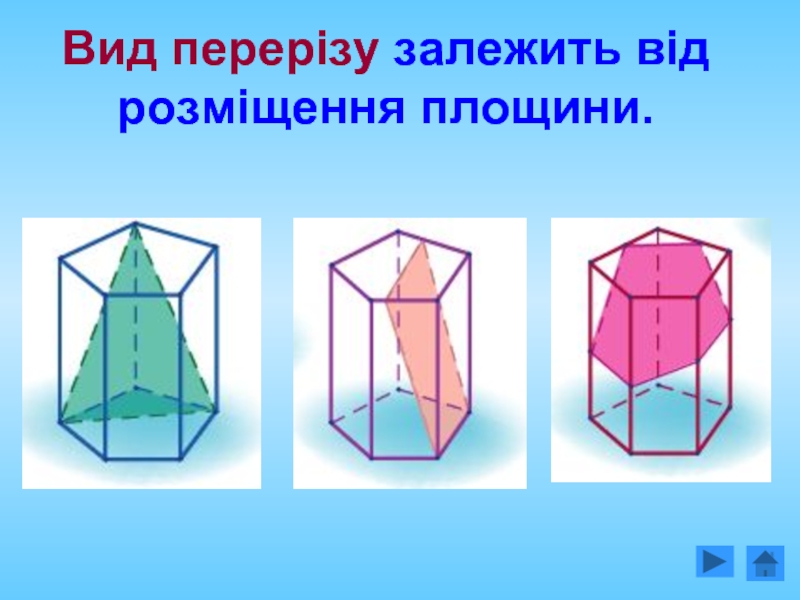
- 9. Вид перерізу залежить від розміщення площини.
- 10. Площину перерізу можна задати: 1. Трьома
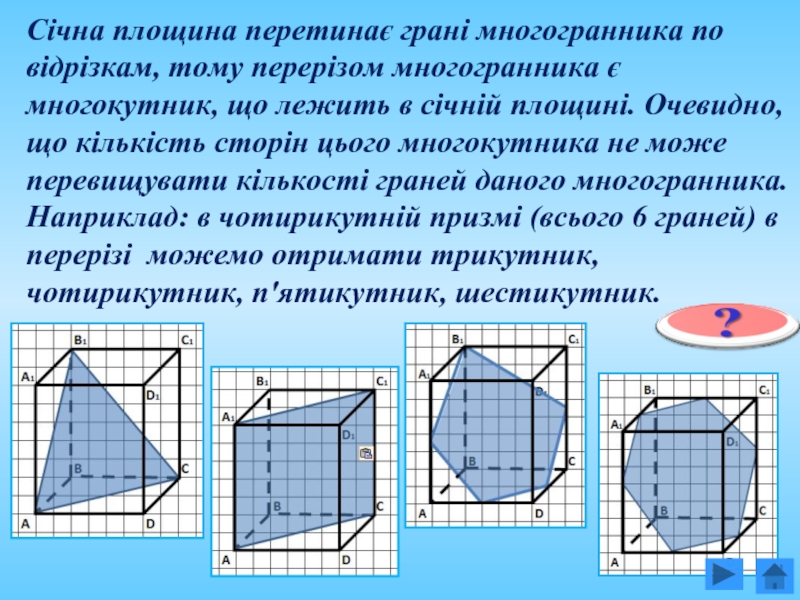
- 11. Січна площина перетинає грані многогранника по відрізкам,
- 12. Які многокутники отримаємо в перерізі п'ятикутної призми площиною?
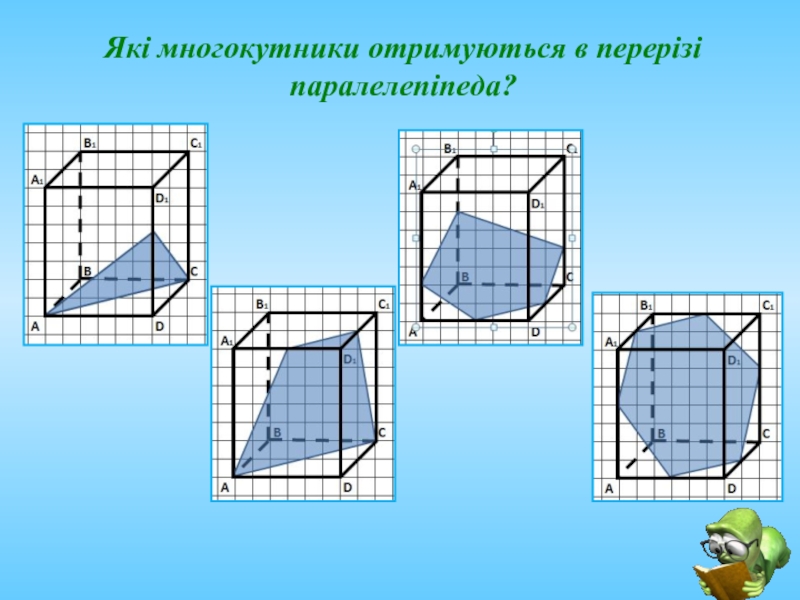
- 13. Які многокутники отримуються в перерізі паралелепіпеда?
- 14. Скільки площин можна провести через виділені елементи?
- 15. Що означає побудувати переріз? Побудувати переріз
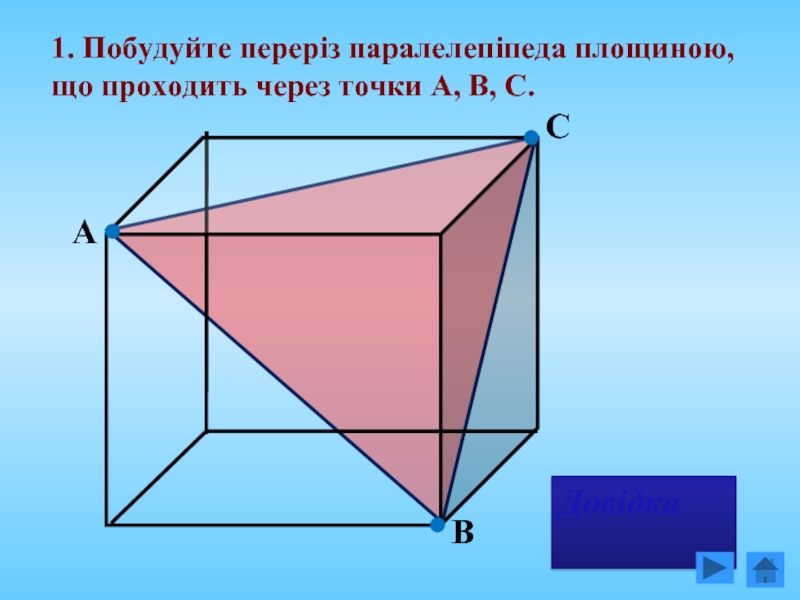
- 16. 1. Побудуйте переріз паралелепіпеда площиною, що
- 17. 2. Побудуйте переріз
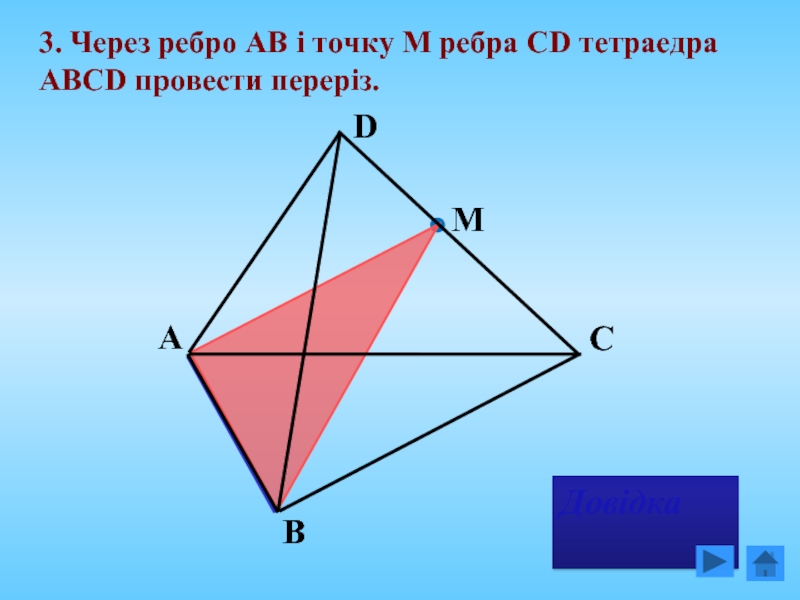
- 18. 3. Через ребро АВ і точку М
- 19. 4. Побудувати переріз, що проходить через
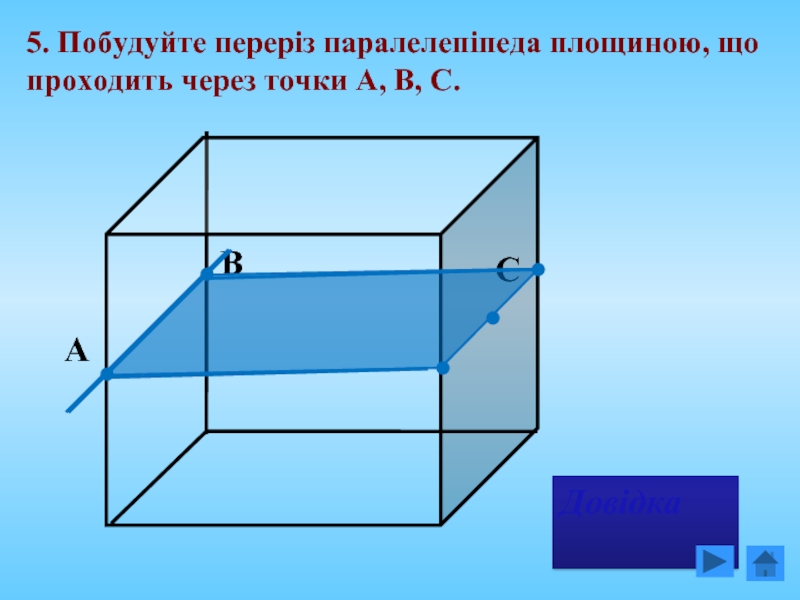
- 20. 5. Побудуйте переріз паралелепіпеда площиною, що проходить
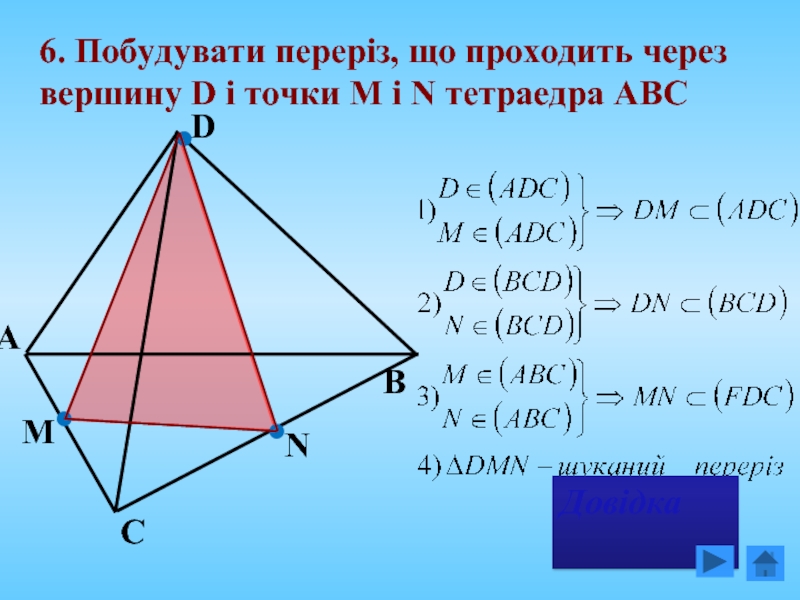
- 21. 6. Побудувати переріз, що проходить через
- 22. Методи побудови перерізів многогранників. Метод слідів. Метод
- 23. Довідковий матеріал. Аксіома 1. Через будь-які
Слайд 2Мета: Повторити геометричні поняття і твердження; навчитися будувати перерізи різними способами;
Слайд 6
Геометричні твердження.
Якщо дві точки прямої лежать на одній площині,
Слайд 7
Геометричні твердження.
Якщо дві паралельних площини перетинаються третьою площиною, то
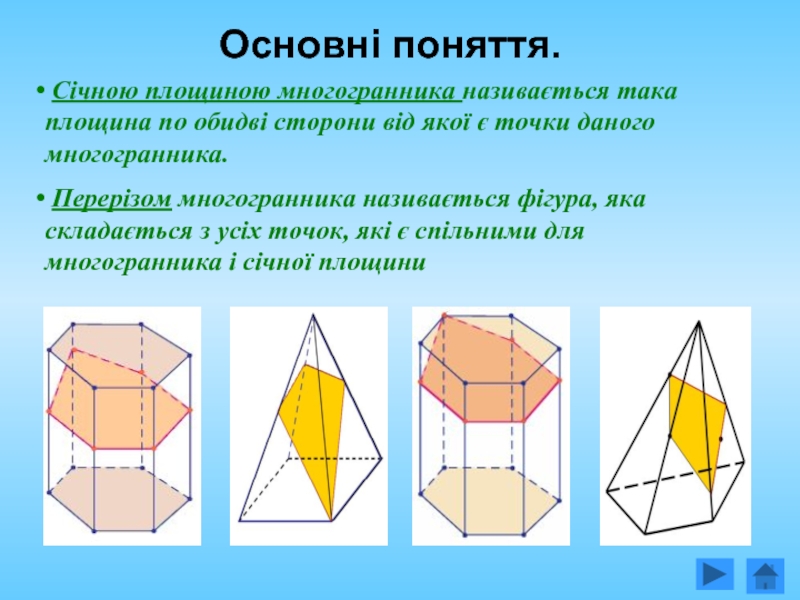
Слайд 8 Січною площиною многогранника називається така площина по обидві сторони від
Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини
Слайд 10Площину перерізу можна задати:
1. Трьома точками, що не лежать на одній
2. Прямою і точкою, що не лежить на ній;
3. Двома прямими, що перетинаються;
4. Двома паралельними прямими;
Слайд 11Січна площина перетинає грані многогранника по відрізкам, тому перерізом многогранника є
Слайд 15Що означає побудувати переріз?
Побудувати переріз многогранника площиною – означає:
в площині
з'єднати ці точки прямою;
знайти точки перетину прямої з ребрами многогранника.
Приклади
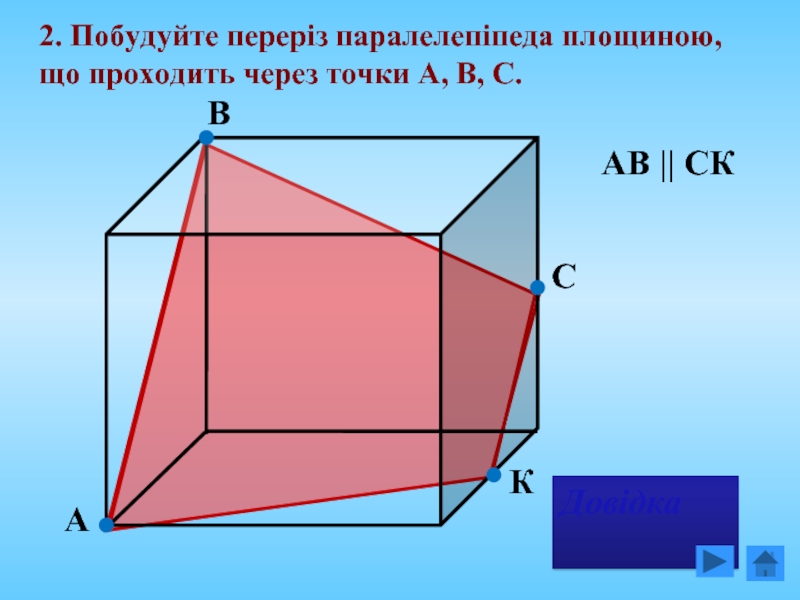
Слайд 17
2. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В,
К
АВ || СК
Довідка
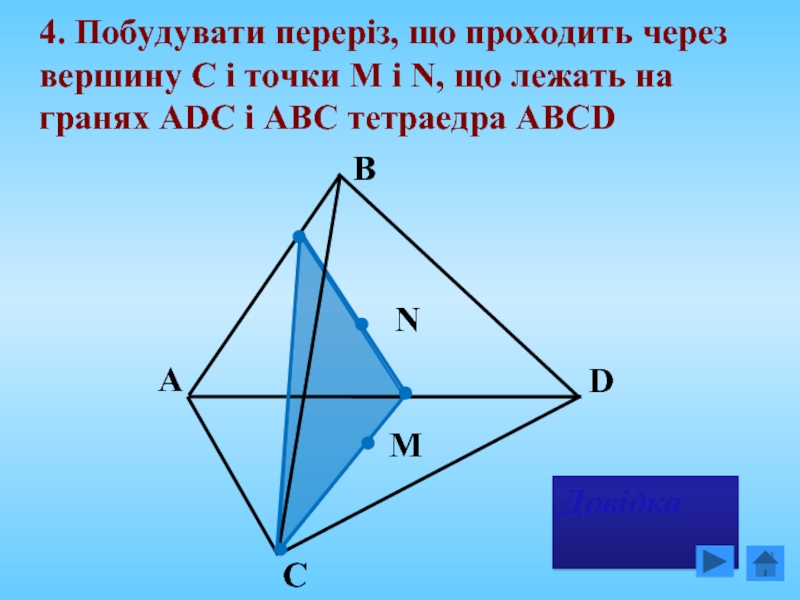
Слайд 19
4. Побудувати переріз, що проходить через вершину C і точки М
N
M
Довідка
Слайд 22Методи побудови перерізів многогранників.
Метод слідів.
Метод внутрішнього проектування або метод допоміжних перерізів
Комбінований
Слайд 23Довідковий матеріал.
Аксіома 1. Через будь-які три точки, що не лежать
Аксіома 2. Якщо дві точки прямої належать площині, то всі точки даної прямої належать площині;
Аксіома 3. Якщо дві площини мають спільну точку, то вони мають спільну пряму на якій лежать спільні точки цих площин;
Наслідки з аксіом:
Через пряму і точку, що не належить даній прямій можна провести площину і до того ж тільки одну;
Через дві прямі, що перетинаються можна провести площину і до того ж тільки одну.
Теорема (ознака паралельності двох площин). Якщо дві прямі, що перетинаються однієї площини відповідно паралельні двом прямим, що перетинаються іншої площини, то ці площини паралельні;
Теорема (властивість паралельних площин). Якщо дві паралельні площини перетнуто третьою, то лінії їх перетину паралельні;
Теорема (ознака паралельності прямої і площини). Якщо пряма, що не належить даній площині, паралельна будь-які прямій цієї площини, то вона паралельна і даній площині.