Методы решения оптимизационных задач презентация

Содержание

Введение Примеры дискретных оптимизационных задач задача о кратчайшем пути: Пусть имеется несколько городов и известны попарные расстояния между соседними городами. При этом два города считаются соседними,

Слайд 1Методы решения оптимизационных задач
М. Лапенок Уральский государственный педагогический университет, г. Екатеринбург

Слайд 2Введение
Примеры дискретных оптимизационных задач

задача о кратчайшем пути: Пусть имеется

несколько городов и известны попарные расстояния между соседними городами. При этом два города считаются соседними, если есть дорога, их соединяющая, и не проходящая через какой-либо другой город. Требуется найти кратчайший путь между некоторой парой городов;

задача оптимального назначения:
Пусть имеется n станков и n деталей, каждую деталь можно обрабатывать на любом станке, но время обработки детали на одном станке может отличаться от времени ее обработки на другом. Пусть эти времена для каждой пары «станок — деталь» заданы. Требуется так организовать производство деталей, т.е. разместить их по станкам, чтобы суммарное время работы было наименьшим ;

задача коммивояжера
Путешественник хочет объехать n городов, побывав в каждом ровно по одному разу, и вернуться в исходный, затратив при этом минимальную сумму на поездку. Затраты па поездку складываются из затрат на переезды между парами городов, а эти затраты заранее известны.

Слайд 3В каждой задаче имеется лишь конечное число вариантов, из которых требуется

осуществить выбор (путей между городами, способов распределения деталей по станкам, маршрутов передвижения путешественника).
Каждому варианту выбора сопоставлена некоторая числовая характеристика (длина пути, суммарное время работы, стоимость поездки).
Требуется выбрать вариант, числовая характеристика которого достигает экстремума.

Методы решения подобных задач
полный перебор (поочередно пересмотреть все варианты и выбрать требуемый);
дискретная оптимизация.

Общие свойства дискретных оптимизационных задач

Слайд 4Типы задач: массовые и индивидуальные задачи.
Все вышеприведенные примеры дают образцы

именно массовых задач.
Индивидуальная задача получается из массовой путем фиксации набора условий.
Например, индивидуальная задача коммивояжера получается из массовой, если зафиксировано число городов и определены затраты на переезды между всеми парами городов.
С каждой конкретной массовой задачей (в дальнейшем просто задачей) будем связывать некоторое число (или несколько чисел), называемое ее размером, которое выражает меру количества входных данных. Например, размером задачи коммивояжера естественно считать число городов n, которые собирается посетить путешественник.

Алгоритмы и их сложности

Слайд 5Говорят, что алгоритм решает некоторую массовую задачу, если он решает любую

ее индивидуальную задачу.
Для оценки качества алгоритмов имеется ряд критериев.
Одним из важнейших таких критериев является понятие вычислительной сложности (или просто сложности) алгоритма.
Неформально, под сложностью алгоритма решения массовой задачи будем понимать максимально возможное число шагов, выполняемых алгоритмом для решения любой из индивидуальных задач, вычисленное как функция размерности задачи.
Под шагом алгоритма будем понимать выполнение "простой" операции, обычно аппаратно реализованной на любой ЭВМ, а именно любой арифметической операции, операции сравнения, пересылки, косвенной адресации и т.п.
При этом будем рассматривать асимптотическую сложность алгоритма, (а не точную сложность, зависящую от конкретного вида машинных команд), т.е. порядок роста числа шагов алгоритма при неограниченном росте размерности задачи.
При сравнении скорости роста двух неотрицательных функций f(n) и g(n) будем использовать следующие понятия.

Алгоритмы и их сложности

Слайд 6При сравнении скорости роста двух неотрицательных функций f(n) и g(n) будем

использовать следующие понятия.
Будем говорить, что функция f(n) имеет порядок роста
не более чем g(n) (запись: f(n) = О(g(n))),
если существуют константы с, N > 0 такие,
что f(n) < c·g(n) для всех n > N.

Говорят, что функция f(n) имеет порядок роста
не менее чем g(n) (запись: f(n) = Ω (g(n)) ),
если существуют константы с, N > 0 такие,
что f(n) ≥ c g(n) для всех n > N.

Алгоритмы и их сложности

Слайд 7Например, справедливы следующие соотношения:
log2n = О(n); n2 = О(2n);

n = Ω (log2n):
На практике алгоритм решения некоторой задачи считается достаточно хорошим, если сложность этого алгоритма есть O(n·p) при некотором р > 0.
В этом случае говорят, что задача полиномиально разрешима,
или, что то же самое, задача может быть решена за полиномиальное время.
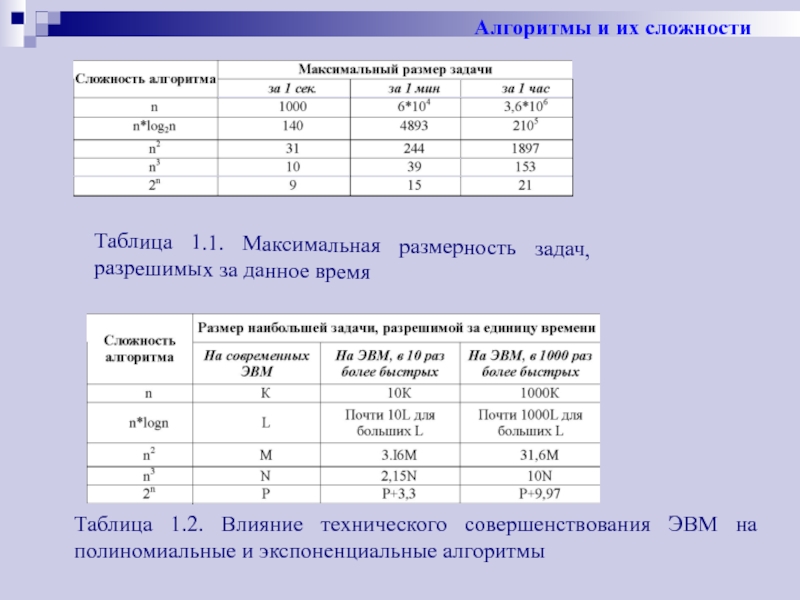
Важность понятия сложности алгоритма хорошо иллюстрируют следующие таблицы.

Алгоритмы и их сложности

Слайд 8Алгоритмы и их сложности
Таблица 1.2. Влияние технического совершенствования ЭВМ на полиномиальные

и экспоненциальные алгоритмы

Таблица 1.1. Максимальная размерность задач, разрешимых за данное время

Слайд 9Пусть для решения некоторой задачи имеется алгоритм сложности n3. Тогда, как

это следует из таблицы 1.2, десятикратное увеличение скорости быстродействия ЭВМ позволит увеличить размер задачи, решаемой за 1 минуту в 2,15 раз. Однако замена этого алгоритма другим, имеющим сложность n2, позволит решать задачу в 6 раз большего размера (см. таблицу 1.1). Если в качестве единицы взять 1 час, то сравнение будет еще более впечатляющим.

Алгоритмы и их сложности

Слайд 10Алгоритмы будем записывать на некотором специальном языке, который назовем упрощенным Паскалем.

В этом языке возможно использование любого типа данных: тип данных какой-либо переменной и ее область действия должны быть ясны либо по ее названию, либо по контексту.
В упрощенном Паскале применяются традиционные конструкции математики и языков программирования такие, как выражения, условия, операторы и процедуры. Операторы языка Паскаль используются, как правило, в соответствии с правилами языка Паскаль, но иногда будут применяться неформальные конструкции такие, как, например,
1) циклы for х ϵ X do Р, т.е. выполнять оператор Р для всех элементов х множества X в произвольной последовательности;
2) x[i] ↔ x[j] — переставить i-ый и j-ый элементы массива; или описание типа: "пусть х — наименьший элемент множества X".
3) Будем также предполагать, что все операторы, записанные в одной строке алгоритма, образуют один составной оператор. Поэтому ключевые слова begin и end, идентифицирующие этот оператор, будут опускаться.

Запись алгоритмов

Слайд 11АЛГОРИТМ 1.1. ВЫБОР МИНИМАЛЬНОГО ЭЛЕМЕНТА
Данные: числовое множество X.
Результат: число minX -

минимальный элемент X
begin
minX := +∞;
for х ϵ X do
if x < minX then minX := x;
end.
Поясним на этом примере понятие сложности алгоритма.
Размером этой задачи естественно считать n — количество элементов во множестве X.
Цикл в строках 3-4 работает ровно n раз. В строке 4 при каждом шаге цикла осуществляется одна операция сравнения и, в худшем случае, одна операция присваивания.
Таким образом, в строках 3 и 4 проводится не более чем 2n операций. С учетом оператора присваивания в строке 2 получаем, что число шагов алгоритма не превосходит 2n+1. Значит сложность этого алгоритма есть О(n).
Алгоритмы такой сложности принято называть линейными.

Запись алгоритмов

Слайд 12Повсюду в дальнейшем будем использовать следующие обозначения. Для произвольного вещественного числа

х через |_x_|
(читается дно х) и |¯х¯| (потолок х) будем обозначить соответственно наибольшее целое число, не превосходящее х, и наименьшее целое, не меньшее х.
Все логарифмы являются логарифмами чисел по основанию 2.
Поэтому вместо log2x будем писать logx.

Запись алгоритмов

Слайд 13Графы и сети

Многие задачи дискретной оптимизации могут быть интерпретированы как задачи

на сетях и графах.
Поэтому повторим основные понятия теории графов.

Слайд 14Графы и сети

Рис. 2.1. Изображение графов и орграфов,
а) Неориентированный граф,

б) Ориентированный граф

Слайд 15Удобно вершины графа считать пронумерованными натуральными числами, и на рисунках сразу

вместо точки ставить соответствующий номер
Число ребер, инцидентных данной вершине, называется степенью вершины.
Вершины степени 1 называют висячими вершинами,
а степени 0 — изолированными.
Например, в графе, изображенном на рис. 2.1.а,
вершины 2, 5, 6 являются висячими.
Степенью захода узла в некотором орграфе называется число дуг, в нее входящих,
степенью исхода — из нее исходящих. Под степенью узла будем понимать сумму степеней исхода и захода данного узла. Например, в орграфе, изображенном на рис. 2.1.б, степень исхода узла 1 равна 2, а степень захода — 1.

Графы и сети

Слайд 16Цепью (соответственно путем) в графе (орграфе)
G = (V,E) назовем чередующуюся

последовательность вершин и ребер
(узлов и дуг) v0,e0, v1, ... ,ek-1, vk такую,
что каждое ребро ek соединяет вершины vk и vk+1
(соответственно исходит из vk и входит в vk+1).
Вершины (узлы) v0 и vk будем называть соответственно началом и концом цепи (пути).
Если все вершины (узлы) цепи (пути) различны, то такую цепь (путь) будем называть
простой цепью (простым путем).

Графы и сети

Слайд 17Цепь в графе (соответственно путь), начальная и конечная вершины (узлы) которого

совпадают, будем называть циклом {контуром).
Если в цикле (соответственно в контуре) все промежуточные вершины различны, то такой цикл (контур) будем на­зывать простым.
Иногда нам будет удобно цепь (путь)
v0,e0,v1, ... , ek-1,vk отождествлять
с множеством ребер (дуг) е0, ... , ek-1
или вершин (узлов) v0,v1, ... ,vk,
его образующих.
Длиной цепи (пути) будем называть число входящих в нее ребер (дуг).

Графы и сети

Слайд 18Графы и сети

Слайд 19Графы и сети

Граф, имеющий ровно одну компоненту связности, будем называть связным.


Из определения вытекает, что неориентированный граф G=(V,E) связен
тогда и только тогда, когда для любых вершин v,w V существует цепь в графе G, их соединяющая.
Всюду в дальнейшем через |А| будем обозначать количество элементов конечного множества А.
Говоря о некотором графе или орграфе G=(V,E),
через n будем обозначать количество вершин (или узлов), то есть будем полагать n=|V|,
через m — количество ребер (или дуг), то есть будем полагать m=|E|.


Слайд 20Графы и сети
Условимся считать, что в графах и орграфах
нет ребер

вида {v,v} и дуг вида (v,v)
(так называемых петель), и,
что для любых v,w V существует не более одного ребра или не более двух дуг им инцидентных
Тогда справедливы неравенства:
m ≤ n∙(n-1 )/2 — для неориентированных графов,
m ≤ n∙(n-l) — для орграфов.


Слайд 21Деревья
Одним из важнейших понятий в теории графов является понятие дерева. Деревом

называется связный неориентированный граф без циклов.

Теорема1. Пусть G = (V,E) — граф, n=|V|, m=|E|. Тогда следующие условия эквивалентны:
G — дерево.
Для любых двух вершин u,v V существует и притом единственная цепь, их соединяющая.
Граф G связен, и m=n-l.
Граф G не содержит циклов, и m=n-l.
Граф G не содержит циклов, и при соединении любых двух несмежных вершин ребром образуется ровно один цикл.


Слайд 22Ориентированный граф без контуров называется корневым деревом, если
имеется в точности один

узел, называемый корнем, в который не входит ни одна дуга
(т.е. степень захода равна нулю);
в каждый узел, кроме корня, входит ровно одна дуга;
для каждого узла существует путь, начинающийся в корне и заканчивающийся в этом узле.

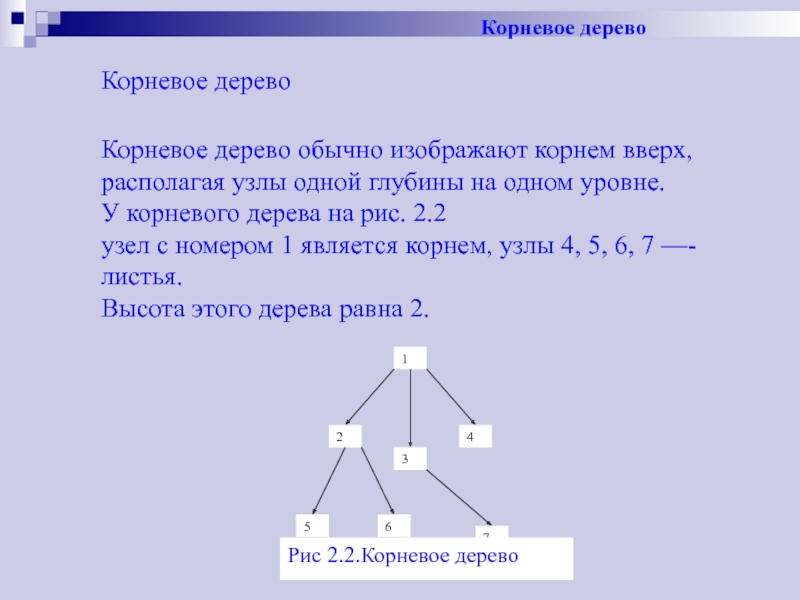
Корневое дерево

Слайд 23Корневое дерево
Корневое дерево

Корневое дерево обычно изображают корнем вверх, располагая узлы одной

глубины на одном уровне.
У корневого дерева на рис. 2.2
узел с номером 1 является корнем, узлы 4, 5, 6, 7 —- листья.
Высота этого дерева равна 2.

Слайд 24Корневое дерево
Пусть G - (V,E) — корневое дерево, v,w

V.
Будем говорить, что узел v является отцом узла w,
a w — сыном узла v, если (v,w) Е.
Если в G существует путь из v до w, то будем говорить, что w — потомок v, a v — предок w.
Вершина, не имеющая сыновей, называется листом. Глубина узла v в корневом дереве — это длина пути из корня в v. При этом глубину корня будем считать равной нулю.
Высота узла v — это длина самого длинного пути из v в какой-нибудь лист.
Высотой дерева будем называть высоту его корня.



Слайд 25Двоичные (бинарные) деревья
Корневое дерево, каждый узел которого имеет не более двух

сыновей, будем называть двоичным деревом.

Методом математической индукции легко доказать следующее утверждение.
Лемма 2.2. Двоичное дерево высоты k содержит не более 2k листьев.

Специфика дискретных оптимизационных задач практически всегда предполагает, что, как ребра графов, так и дуги орграфов, снабжены некоторой числовой характеристикой.

Практический смысл этих характеристик может быть самым разнообразным.

Например, в задачах, сформулированных ранее, это были:
длина дороги между соседними городами (задача о кратчайшем пути), время обработки конкретной детали на конкретном станке (задача оптимального назначения), стоимость проезда из одного города в другой (задача коммивояжера).



Слайд 26Двоичные (бинарные) деревья
Граф (орграф) будем называть взвешенным,
если задана функция с:

Е→R, иначе говоря,
каждому ребру (дуге) из Е
поставлено в соответствие вещественное число с(е). Число с(е) назовем весом ребра (дуги) е.

Впрочем, в зависимости от специфики той или иной задачи дискретной оптимизации,
число с(е) будем также называть стоимостью ребра (дуги) е,
или пропускной способностью ребра (дуги) е.



Слайд 27Машинное представление графов и сетей
Ориентированный взвешенный граф будем
называть сетью.



Таким образом, взвешенный граф или сеть задаются тройкой G = (V,E,c).

Задать граф (орграф) — значит описать множества его вершин (узлов) и ребер (дуг),
а в случае взвешенного графа или сети, описать также функцию весов с: Е→R.
Мы будем предполагать, что вершины графов и узлы сетей занумерованы натуральными числами от 1 до n. Поэтому для описания множества вершин (узлов),
если не указана какая-нибудь дополнительная информация,
достаточно задать одно число —
число вершин (узлов) n.



Слайд 28Машинное представление графов и сетей
Разберем несколько способов машинного представления графа

(орграфа) G = (V,E), где n= |V |, m= | Е |.
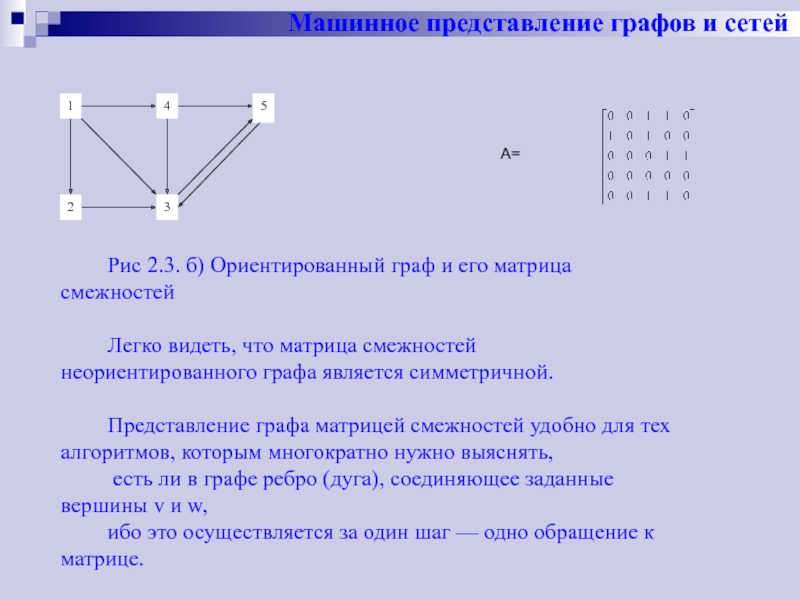
Матрица смежностей
определяется как матрица А размера n х n,
в которой A[v,w]=l тогда и только тогда,
когда ребро {v,w} (соответственно дуга (v,w)) имеется в графе (орграфе),
и A[v,w]=0 в противном случае.



А=


Рис 2.3. а) Неориентированный граф и его матрица смежностей,

Слайд 29Машинное представление графов и сетей


А=

Рис 2.3. б) Ориентированный граф и

его матрица смежностей

Легко видеть, что матрица смежностей неориентированного графа является симметричной.

Представление графа матрицей смежностей удобно для тех алгоритмов, которым многократно нужно выяснять,
есть ли в графе ребро (дуга), соединяющее заданные вершины v и w,
ибо это осуществляется за один шаг — одно обращение к матрице.


Слайд 30Машинное представление графов и сетей



Однако, для ответа на вопросы
«к

каким вершинам (узлам) ведут ребра (дуги) из V?» и «какова степень вершины (узла) v?»
нужно просмотреть всю строку матрицы с номером v.

Следовательно, сложность ответа на любой из этих вопросов для фиксированной вершины есть О(n).

Матрица смежностей является достаточно удобным способом представления графа, если не принимать во внимание затраты памяти: граф на n вершинах требует памяти пропорционально n2, независимо от числа ребер.

Особенно сильно этот недостаток проявляется для разреженных графов, т.е. таких, в которых число ребер невелико по сравнению с числом вершин: в этом случае матрица смежностей почти целиком состоит из нулей.

Слайд 31Машинное представление графов и сетей



Взвешенный граф (или сеть) G =

(V,E,c),
может быть задан в ЭВМ матрицей весов А,
в которой полагают A[v,w] = c({v,w}) - весу ребра {v,w} (или весу дуги c((v,w)) ),
и A[v,w] = ∞ — для ребер (дуг), отсутствующих в графе (сети).
Иногда, в зависимости от специфики конкретной задачи, уточняют знак бесконечности, выбирая либо +∞, либо - ∞.

Слайд 32Машинное представление графов и сетей



Более экономным, чем матрица смежностей, и

универсальным способом является представление графов и сетей списками смежностей.
Списком смежностей для вершины (узла) v называется список всех вершин (узлов) w, смежных с v.
Граф (орграф) представляется с помощью п списков смежностей: по одному для каждой вершины (узла). Точнее, каждый элемент такого списка является записью r, имеющей два поля. Первое поле, обозначим его r^.строка, предназначается для хранения вершин, смежных дан­ной; второе — r^.след — для ссылки на следующую запись в списке. При этом будем считать, что r^.след = nil для последней записи в списке.

Слайд 33Машинное представление графов и сетей



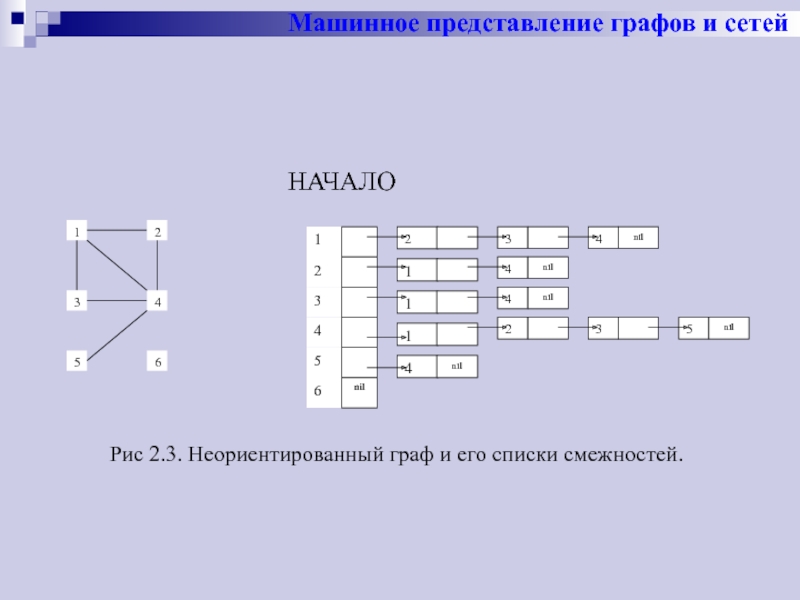
Начало каждого списка хранится в массиве

НАЧАЛО,
а именно, HAЧAJIO[v] является указателем на начало списка, соответствующего вершине (узлу) v;
если v — изолированная вершина (узел), то полагаем HAЧAЛО[v] = nil.
Весь такой список для не­ориентированного графа будем обозначать ЗАПИСЬ[v].
Ясно, что в этом случае каждое ребро (v, w) графа представлено дважды:
вершиной w в списке ЗАПИСЬ[v] и вершиной v в списке ЗАПИСЬ[w].

Слайд 34Машинное представление графов и сетей



НАЧАЛО
Рис 2.3. Неориентированный граф и

его списки смежностей.

Слайд 35Для ориентированных графов возможны два способа формирования списков смежностей.
В первом

в список ЗАПИСЬ[v] включаются лишь те узлы w, для которых (v, w) E,
т.е. те узлы, к которым ведут дуги из w.
Такой список будем обозначать СЛЕД[v]. Д
ругой способ — включать в список ЗАПИСЬ[v] лишь те узлы w, из которых идут дуги в узел v.
Этот список будем обозначать ПРЕДШ[v].

Для представления взвешенного графа или сети достаточно в соответствующих списках смежностей отвести одно дополнительное поле для весов ребер или дуг.

Машинное представление графов и сетей


Слайд 36Проанализируем способ представления графов и сетей списками смежностей.
Понятно, что объем памяти,

необходимый для представления графа или сети, имеет порядок n+m, что, вообще говоря, лучше, чем представление матрицей смежности. Особенно заметным этот выигрыш по памяти становится для редких графов (m ˂˂ n2).
Ограничимся далее случаем неориентированного графа. Для ответа на вопросы
имеется ли в графе (орграфе) ребро {v,w} (дуга (v,w))?
к каким вершинам (узлам) ведут ребра (дуги) из V?
какова степень вершины (узла) v?
достаточно просмотреть список ЗАПИСЬ[v].
Сложность такого просмотра есть О(n) — такая же, как и в случае матрицы смежностей.

Машинное представление графов и сетей


Слайд 37Однако, если определять степень всех вершин графа,
то здесь сложность ответа

будет O(n+m), так как каждое ребро смотрится ровно два раза,
в то время как для матрицы смежностей вычислительная сложность такого просмотра есть О(n2).
Списки смежностей являются достаточно удобным инструментом для решения задач добавления или удаления ребер из графа.
Осуществляются подобные процедуры стандартными средствами для работы со списками.
Понятно, что сложность процедуры добавления ребра является константой, если известно, что данного ребра в графе нет, и имеет сложность О(n),
если предварительно требуется осуществить поиск для ответа на вопрос о том, есть или нет данное ребро в графе. Аналогично обстоит дело и с процедурой удаления ребра (дуги) из графа (соответственно орграфа).

Машинное представление графов и сетей


Слайд 38Докажите, что в любом графе число вершин нечетной степени четно.
В некоторых

задачах удобно представлять граф связанными списками смежностей. А именно, каждая запись в списке 3AПИСЬ[v] имеет еще одно поле, где в записи, содержащей вер­шину w, в дополнительном поле ставится ссылка на ту запись списка 3AПИСЬ[w], которая содержит вершину v. Напишите алгоритмы удаления и добавления ребра в граф, заданный связанными списками смежностей.
Предложите алгоритм, сложности О(n), записывающий все вершины в списке ЗАПИСЬ[v] в обратном порядке.
Пусть некоторый граф задан матрицей смежностей.
Рассмотрим следующую процедуру:
begin х:=0;
for р:=1 to n do
for q:=p to n do
х:= х + A[p,q];
end.
Чему будет равен х в результате работы этой процедуры?

ЗАДАЧИ


Слайд 39В тех случаях, когда нет необходимости добавлять и удалять ребра или

дуги из графа, все списки смежностей вместе с массивом НАЧАЛО можно упаковать в один массив, называемый массивом смежностей.
Массив смежностей представляет собой одномерный массив А длины (n+2m+2) для неориентированного графа, и (n+m+2) — для ориентированного.
Рассмотрим случай неориентированного графа. Первые n+1 элементов массива А являются адресной частью, а именно, значением A[v] (v=l,2,...,n) является адрес (индекс) в массиве А, начиная с которого в А записаны подряд все вершины, смежные с вершиной v; А[n+1] указывает на конец массива.

Машинное представление графов и сетей


Слайд 40Поскольку каждое ребро графа встречается в таком массиве дважды (и имеет

индексы в массиве от А[n+2] до А[n+1]-1), то массив действительно имеет длину n+2m+2. Отсюда следует, что этот способ представления графа требует меньше памяти, чем матрица смежностей и чем списки смежностей (так как в последнем случае нет нужды в храпении ссылок на следующие записи).
Для ориентированных графов в массиве смежностей, так же как и в списках смежностей, можно хранить дуги по одному разу, записывая либо только исходящие дуги, либо только входящие. И в том, и в другом случае массив будет иметь длину n+m+2 .

Машинное представление графов и сетей


Слайд 41



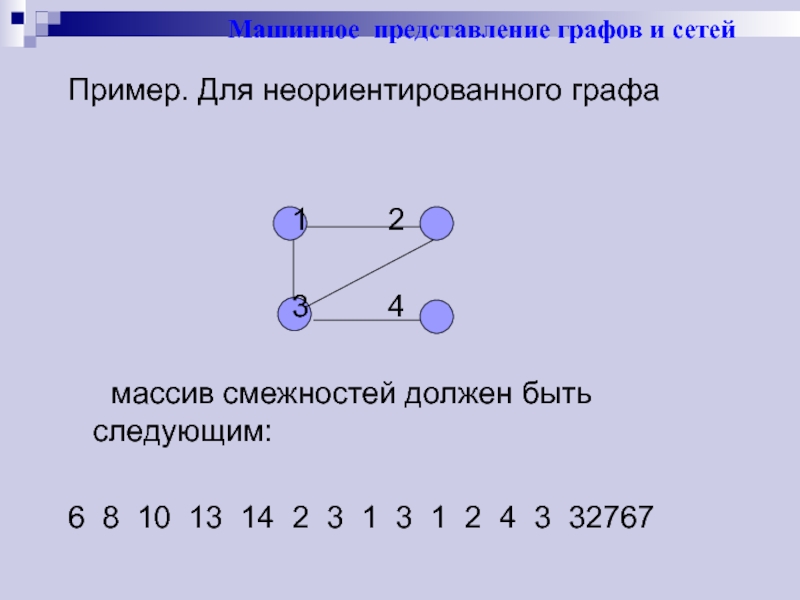
Пример. Для неориентированного графа


1 2

3 4

массив смежностей должен быть следующим:

6 8 10 13 14 2 3 1 3 1 2 4 3 32767

Машинное представление графов и сетей


Слайд 42Поясним на примере:
Количество вершин n = 4
Количество ребер m = 4
Ниже

перечислены для указанного в примере графа вершины и соответствующие каждой вершине смежные вершины.
1: 2, 3;
2: 1, 3;
3: 1, 2, 4;
4: 3.

Машинное представление графов и сетей


Слайд 43



Для взвешенного неориентированного графа

(25)
1 2
(4) (0)
3 4
(7)
массив смежностей должен быть следующим:

6 10 14 20 nil 2 25 3 4 1 25 3 0 1 4 2 0 4 7 3 7 nil
22 – количество элементов массива 32767

Машинное представление графов и сетей


Слайд 44Поясним
Количество вершин n = 4
Количество ребер m = 4
Ниже перечислены для

указанного в примере графа вершины и соответствующие каждой вершине пары вида (вес, смежная вершина).

1: (25, 2); (4, 3);
2: (25, 1); (0, 3);
3: (4, 1); (0, 2); (7, 4);
4: (7, 3);

Машинное представление графов и сетей


Слайд 45Вернемся к предложенным на прошлой паре задачам.
После решения задачи «Предложите алгоритм,

сложности О(n), записывающий все вершины в списке ЗАПИСЬ[v] в обратном порядке»
Программа, работающая по указанному алгоритму должна выдавать соответствующие каждой вершине пары вида (вес, смежная вершина) в обратном порядке.

1: (4, 3); (25, 2);
2: (0, 3); (25, 1);
3: (7, 4); (0, 2); (4, 1);
4: (7, 3).

Машинное представление графов и сетей


Слайд 46Входные данные содержат описание графа,
заданного массивом смежности.
В первой строке n

- число элементов в массиве.
Далее построчно расположен массив
смежности (не более 10 чисел в одной строке). Последний элемент массива равен 32767.

22
6 10 14 20 22 2 25 3 4 1
25 3 0 1 4 2 0 4 7 3
7 32767

Решение задачи


Слайд 47На выходе программа построчно выдает для каждой вершины (начиная с первой

и до n-ой) пары вида
(вес, смежная вершина) в прямом порядке.
А затем для каждой вершины (опять начиная с первой и до N-ой) пары вида
(вес, смежная вершина) в прямом порядке.
Количество вершин n = 4
Cписок смежности в прямом порядке:
1: (25, 2); 1: (4, 3);
2: (25, 1); 2: (0, 3);
3: (4, 1); 3: (0, 2); 3: (7, 4);
4: (7, 3);

Cписок смежности в обратном порядке:
1: (4, 3); 1: (25, 2);
2: (0, 3); 2: (25, 1);
3: (7, 4); 3: (0, 2); 3: (4, 1);
4: (7, 3);

Решение задачи


Слайд 48// Библиотеки
#include
#include
#include
#include

using namespace std;
void main() {
int n

= 0;
vector < pair < int, pair > > g; // ребра: вес - вершина 1 - вершина 2

freopen("in.txt","r", stdin);
freopen("out.txt","w", stdout);

int temp;
cin >> temp;// сколько чисел вообще считывать
int *temp_ar = new int [temp];//весь массив смежностей
int *temp_ar_number = new int [temp];//вспомогательный массив для хранения только позиций (адресов)

Программа на C++


> temp;// сколько чисел вообще считывать int *temp_ar = new int [temp];//весь массив смежностей int *temp_ar_number = new int [temp];//вспомогательный массив для хранения только позиций (адресов) Программа на C++ ">

Слайд 49for (int i = 0; i < temp; i++) {
temp_ar_number[i] =

-1;
}
for(int i = 0; i < temp; i++) {
cin >> temp_ar[i]; // считали из файла массив, где все входные данные (весь массив смежности)
}
for (int i = 0; i < temp; i++){
temp_ar_number[i] = temp_ar [i]; //массив с адресной частью
if (temp_ar[i] == temp) {
n = i;
break;
}
}
// Определили количество вершин графа (в соответствии с придуманной и реализованной нами структурой входного файла)

Программа на C++


Слайд 50 cout

массива смежности
int fict = 1;//фиктивная переменная начало ребра
int k;
for (int i = 0; i < temp; i++){
int numb_begin = temp_ar_number[i]-1;
//взяли первое определяющее число массива
int numb_end = temp_ar_number[i+1]-1;
//взяли второе определяющее число массива
for (int j = numb_begin; j < numb_end; j+=2){
g.push_back(make_pair(temp_ar[j+1], make_pair (fict, temp_ar[j])));
}
fict++;
if (numb_end == (temp-1)) break;
}

Программа на C++


Слайд 51Вывод (печать) массива смежности
cout

= 0; i < g.size(); i++ ) {
cout << g[i].second.first<<": (" << g[i].first << ", " << g[i].second.second << "); ";
k = i+1;
if(g[i].second.first != g[k].second.first){
cout << "\n";
}
}

Программа на C++


Слайд 52Формирование массива смежности
vector < pair < int, pair > > g_convert;

// обратные списки смежности
fict = 1;
for (int i = 0; i < temp; i++){
int numb_begin = temp_ar_number[i]-1;//взяли первое определяющее число массива
int numb_end = temp_ar_number[i+1]-1;//взяли второе определяющее число массива

for (int j = numb_end; j > numb_begin; j-=2){
g_convert.push_back(make_pair(temp_ar[j-1], make_pair (fict, temp_ar[j-2])));
}
fict++;
if (numb_end == (temp-1)) break;
}

Программа на C++


Слайд 53Вывод массива смежности
cout

0; i < g_convert.size(); i++) {
cout << g_convert[i].second.first<<": (" << g_convert[i].first << ", " << g_convert[i].second.second << "); ";
k = i+1;
if( g_convert[i].second.first != g_convert[k].second.first){
cout << "\n";
}
}
}

Программа на C++


Слайд 54Обучающийся
1) рисует взвешенный граф,
2) «вручную» пишет на листке массив

смежности (в прямом и обратном порядках),
3) подписанный листок с нарисованным графом сдает преподавателю (мне!!!),
4) пишет программу на Java или на Паскале, которая решает задачу,
5) после проверки правильности ее работы преподаватель проверяет работоспособность программы на нескольких графах (скорее всего, на графах, предложенных одногруппниками),
6) объясняет код и получает «плюсик».

Индивидуальное задание для реализации на уроке (прямо сегодня!!!)


Слайд 55Сортировка является неотъемлемой частью многих алгоритмов решения математических задач.
Задача сортировки

формулируется следующим образом:
Дана последовательность из n элементов a1,...,an, выбранных из множества, на котором задано отношение линейного порядка.
Требуется найти перестановку
s = (s(l),…,s(n)) индексов, для которой
as(1) ≤ as(2) ≤ ... ≤ as(n),
т.е. расположить элементы данной последовательности в неубывающем порядке
(или в невозрастающем, т.е. as(1) ≥ as(2) ≥ ... ≥ as(n)).

Сортировка данных


Слайд 56При формулировании задачи сортировки в общем виде информацию о последовательности элементов

можно получать только с помощью операции сравнения двух элементов.
Пусть а1,...,аn - последовательность сортируемых элементов.
Не ограничивая общности, можно считать, что элементы заданной последовательности помещены в некоторый массив А
Не ограничивая общности, можно считать, что элементы заданной последовательности помещены в некоторый массив А в том же порядке,
m.е. A[i] = ai при i = 1,2,...,n.

Сортировка данных


Слайд 57Алгоритм сортировки выбором

Данные: массив А[1..n].
Результат:
массив А[1..n] такой, что А[1]

≤ А[2] ≤ ... ≤ A[n].
begin
procedure MIN(i):
begin for j = i to n do
if A[i] < A[j] then A[i]↔A[j];
end;
begin (* главная программа *)
for i := 1 to n-1 do MIN(i);
end;
end.

Сортировка выбором


Слайд 58Процедура MIN(i)
выбирает минимальный элемент из
массива аi,...,аn и ставит его

на первое место, т.е. на место ai.
Алгоритм начинает работу с вызова процедуры MIN(l), которая перемещает
на первое место наименьший элемент исходного массива.
Далее процедура повторяется для массива
а2,...,аn и т.д.

Сортировка выбором


Слайд 59Сортировка выбором имеет вычислительную сложность O(n2).
Действительно, в процедуре MIN(i) осуществляется (n-i)

операции сравнения и, в худшем случае, (n-i) операции обмена.
Значит, общее число шагов, выполняемое процедурой MIN(i) пропорционально (n-i).

Число сравнений в алгоритме
(n - 1) + (n - 2) + ... + 1 = n(n - 1 )/2
Т.е. сложность алгоритма есть O(n2).

Сортировка выбором


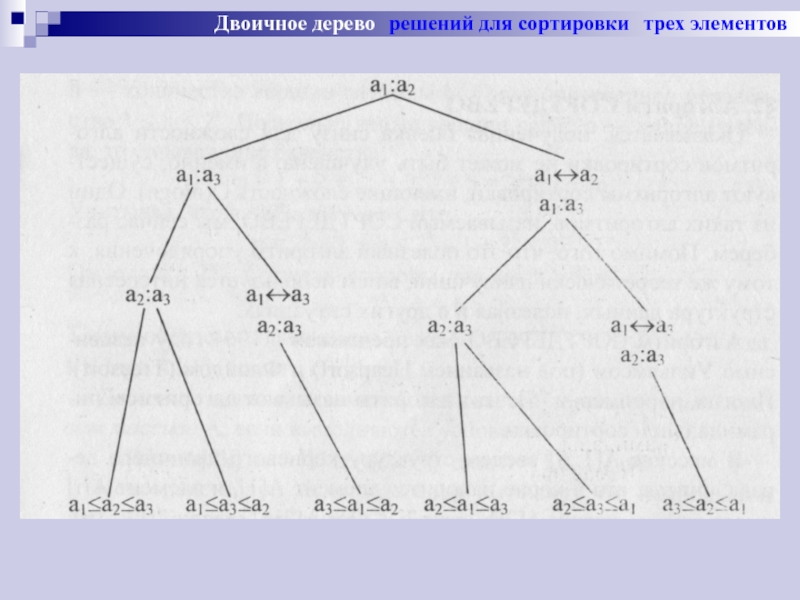
Слайд 60Приведем теорему, позволяющую оценить снизу сложность любого алгоритма сортировки.

В любом алгоритме,

упорядочивающем с помощью сравнений,
на упорядочение последовательности из n элементов
тратится не менее c∙n∙loq n сравнений
при некотором с > 0 и достаточно большом n.

Для доказательства представим алгоритм в виде корневого дерева.
Любой алгоритм, упорядочивающий с помощью сравнений, можно схематично представить в виде корневого дерева, называемого двоичным деревом решений.
Это дерево можно рассматривать как блок-схему алгоритма сортировки, в котором показаны все сравнения элементов и исходы алгоритма.
Вершины дерева (кроме листьев) соответствуют сравнениям элементов, при этом корень дерева соответствует первому сравнению, осуществляемому алгоритмом.
Сыновья вершин изображают возможные исходы сравнения отца.
Листья соответствуют исходу алгоритма в зависимости от начальных значений переменных.

Сортировка данных


Слайд 61Двоичное дерево решений для сортировки трех элементов

Слайд 62Поскольку, всякое двоичное дерево высоты к имеет не более 2к листьев,

то получаем, что должно выполняться неравенство 2к > n!,
т.к. листьев в двоичном дереве решений должно быть не меньше, чем перестановок из n элементов.
Отсюда, k > log n!
Осталось заметить, что при n > 1 справедлива следующая цепочка неравенств:
n! ≥ n(n - 1 )(n - 2)... () ≥ (n/2)n/2, так что
log n! ≥ log( n/2 )n/2 = n/2 log n/2 ≥ n/4 log n
Итак, k ≥ n/4 log n — полученное неравенство завершает доказательство теоремы.

Сортировка данных


Слайд 63Алгоритм сортировки, называемый СОРТДЕРЕВО, имеет сложность O(n log n).
В разных

учебниках он называется: алгоритмом пирамидальной сортировки, Heapsort или Treesort.
Определим структуру корневого двоичного дерева в массиве А[1..n], считая,
что в корне находится элемент А[1],
и элемент A[i] имеет двух сыновей:
A[2i] (если 2i ≤ n) и A[2i+1] (если 2i+1 ≤ n).
Такую структуру назовем двоичным деревом массива А.

Алгоритм СОРТДЕРЕВО


Слайд 64Алгоритм СОРТДЕРЕВО
Лемма.
Двоичное дерево массива длины n имеет высоту

Напомним, что высота

корневого дерева есть по определению длина самого длинного пути из корня до какого-нибудь листа. Например, на рис.3.2 это путь до листа, в котором находится число 7. Легко видеть, что длина этого пути равна 3.




Слайд 65Пусть k - высота двоичного дерева массива длины n.
Для всех

s < k в дереве имеется ровно 2s вершин глубины s. Пусть h — количество вершин глубины k.
Тогда справедливо неравенство 1 < h < 2k. Поскольку число вершин равно n — длине массива, то справедливо равенство:
n = 1 + 2 + ... + 2k-1 + h = 2k - 1 + h.
Учитывая, что h ≤ 2k, получаем, что
n = 2k - 1 + h ≤ 2k - 1 + 2k < 2k+1.
Отсюда n < 2k+1. С другой стороны, так как h ≥ 1, то
n= 2k - 1 + h ≥ 2k.
Таким образом, справедливо неравенство 2k ≤ n ≤ 2k+1.
Отсюда, k ≤ logn ≤ k+1, то есть k =

Алгоритм СОРТДЕРЕВО



Слайд 66Двоичное дерево массива А называется сортирующим деревом массива А, если выполняются

условия:
А[k] ≥ А[2 k] и А[k] ≥ А[2 k +1] для к = l,2,....
Непосредственно из определения вытекает, что наибольший элемент массива находится в корне его сортирующего дерева.

Легко видеть также, что двоичное дерево, изображенное на представленном выше рис., не является сортирующим.
Именно на представлении массива сортирующим деревом основан один из теоретически наилучших алгоритмов сортировки данных — СОРТДЕРЕВО.

Алгоритм СОРТДЕРЕВО




Слайд 67На первом этапе двоичное дерево массива А преобразуется в сортирующее. Процедуру,

осуществляющую это преобразование, будем называть ПСД.
Затем, поскольку по свойству сортирующего дерева,
элемент в корне, а именно, А[1] является наибольшим в А, то, переставляя А[1] и А[n],
и удаляя А[n] из дерева, получим массив А[1.. n-1] и A[n] = max А[1..n]. Теперь преобразуем А[1..n-1] в сортирующее дерево,
затем переставим А[1] и А[n-1] и удалим А[n-1]. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда А[1],...,А[n] — упорядоченная по неубыванию последовательность.

Алгоритм СОРТДЕРЕВО




Слайд 68Перейдем к формальному описанию алгоритма СОРТДЕРЕВО. Начнем с описания процедуры ПСД

(построение сортирующего дерева). В его основе лежит рекурсивная процедура ПЕРЕСЫПК(i,j), имеющая параметры i и j. Они задают область ячеек массива А, которая в результате процедуры ПЕРЕСЫПКА будет обладать свойством сортирующего дерева, при этом его корень помещается в вершину i.

Алгоритм СОРТДЕРЕВО




Слайд 69Алгоритм СОРТДЕРЕВО
АЛГОРИТМ 3.2. СОРТДЕРЕВО
Данные: массив элементов А[1..n].
Результат: массив элементов

А[1..n], упорядоченный по неубыванию, то есть А[1] ≤ А[2] ≤ ... ≤ А[n].
begin
ПСД; (* вначале строится сортирующее дерево *)
for i := n downto 2 do
begin
A[l] ↔ A[i];
ПЕРЕСЫПКА( 1,i-1)
end;
end




Слайд 70procedure ПСД;
begin
for i := downto 1 do ПЕРЕСЫПКА(i,n)
End


Ниже дано формальное описание

процедур ПЕРЕСЫПКА. Без формального описания используется функция MAXCЫH(i), значением которой является тот сын i, который со­держит наибольший из элементов A[2i] и A[2i+1].

Алгоритм СОРТДЕРЕВО




Слайд 71procedure ПЕРЕСЫПКА( i ,j);
begin
if i ≤ then (* если i — не

лист *)
begin k := MAXCЫH(i);
if A[i] < A[k] then
begin
A[i]↔ A[k]; ПЕРЕСЫПКА(k,j)
end;
end;
end;

Алгоритм СОРТДЕРЕВО




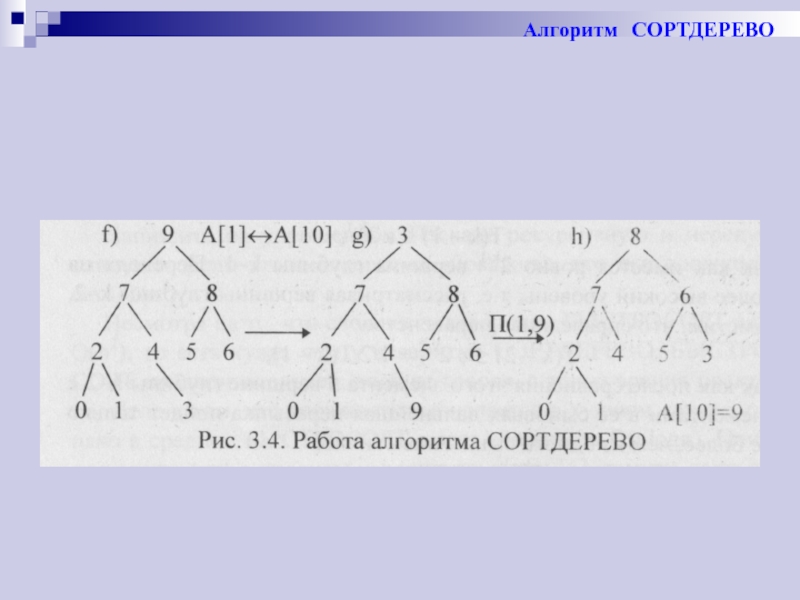
Слайд 72Разберем пример, иллюстрирующий работу обеих этих процедур
Пусть задан числовой массив А[1…10]:
I 1 2 3 4 5 6 7 8 9 10
А[I] 2 3 6 1 4 5 8 0 7 9

Алгоритм

СОРТДЕРЕВО




Слайд 73Алгоритм СОРТДЕРЕВО



Слайд 74Алгоритм СОРТДЕРЕВО



Изобразим окончательный результат в виде таблицы:
I 1 2 3 4 5 6 7 8 9 10
A[I] 9 7 8 2 4 5 6 0 1 3

Слайд 75Алгоритм СОРТДЕРЕВО



Слайд 76Алгоритм СОРТДЕРЕВО



На рис.3.4 дерево f) является сортирующим деревом исходно­го массива

А, полученным в результате работы процедуры ПСД. Затем происходит перестановка А[1] и А[10] (дерево g) ). К дере­ву g) применяется процедура ПЕРЕСЫПКА(1,9), в результате которой число 3 проходит путь по правым ветвям из корня дере­ва до листа. Затем вновь происходит перестановка корня с лис­том и т.д. В результате получится массив А, упорядоченный по возрастанию.

Слайд 77Поиск в графе



Поиск в графе
Большинство алгоритмов на графах основаны на систематическом

переборе всех вершин графа, при котором каждая вершина просматривается в точности один раз,
при этом переход от уже рассмотренной вершины к еще не рассмотренной вершине осуществляется по ребрам графа.
В этой главе будут рассмотрены два стандартных, широко используемых на практике метода такого перебора: поиск в глубину и поиск в ширину.
Оба этих метода поиска будут описаны только для неориентированных графов.

Слайд 78Поиск в глубину



Поиск начинается с некоторой фиксированной вершины v, называемой

корневой вершиной поиска или корнем. При этом считаем v просмотренной вершиной. Затем выбираем какое-нибудь ребро {v,w}, инцидентное v, проходим его и попадаем в вершину w.

Слайд 79Поиск в глубину



Тот факт, что в процессе поиска использовано именно

ребро {v,w} отмечается обычно следующим образом.
Ребро {v,w} ориентируется из v в w. Полученную дугу (v,w) считают дугой корневого дерева с корнем v.
Такое дерево называется ПВГ-деревом с корнем v, или короче ПВГ(v)—деревом.
При переходе от v к w, вершина v объявляется отцом вершины w
и обозначается OTEЦ[w], вершина w объявляется просмотренной, и поиск продолжается из вершины w.

Слайд 80Поиск в глубину



В общем случае, когда мы находимся в некоторой

вершине v, возникают две возможности:
1) Все вершины, смежные с v, уже просмотрены. В этом случае возвращаемся к вершине ОТЕЦ[v] и продолжаем поиск из нее, а вершину v с этого момента считаем использованной.

Слайд 81Поиск в глубину



2) Существует еще не просмотренная вершина w, смежная

с вершиной v. Тогда ребро {v,w} превращаем в дугу (v,w),
добавляя ее к ПВГ(v)-дереву;
полагаем ОТЕЦ[w]=v;
проходим по дуге из v в w и продолжаем поиск из w.

Слайд 82Поиск в глубину



Поиск в глубину завершается тогда, когда все вершины

графа будут просмотрены. Здесь возможны две ситуации:
1) Корневая вершина использована (т.е. все смежные с ней вершины просмотрены), однако в графе еще есть не просмотренные вершины. В этом случае выбираем произвольную не просмотренную вершину, объявляем ее корнем и вновь начинаем поиск уже из этой вершины. Такая ситуация возникает только в случае несвязного графа.
2) Корневая вершина и все другие использованы. Поиск на этом заканчивается.

Слайд 83Поиск в глубину



Представим формальное описание изложенного алгоритма поиска в глубину,

основанную на рекурсивной процедуре ПВГ(v) — поиск в глубину из вершины v. В рассматриваемом алгоритме связность графа не предполагается.
АЛГОРИТМ Поиск в глубину.1
Данные: неориентированный граф G=(V,E), заданный списками смежностей ЗАПИСЬ[v].
Результаты: массив ОТЕЦ, множество Т.
procedure ПВГ (v); (*поиск в глубину с корнем v)
begin METKA[v]:=l;
for w ЗАПИСЬ[v] do
if METKA[w]=0 then
begin OTEЦ[w]:=v; T:=T{(v,w)}; ПВГ(w);
end;
end;
begin (*Главная программа)
T := Ø;
for v V do METKA[v]:=0; (*инициализация)
for v V do
if METKA[v]=0 then
begin OTEЦ[v]:=nil; ПВГ(v);
end;
end.

Слайд 84Поиск в глубину



Примечание.
Массив МЕТКА, используемый в алгоритме имеет по одному

элементу для каждой вершины графа и служит указателем на то, что просмотрена или нет данная вершина.
Считаем, что METKA[v]=0, если v не просмотрена, и METKA[v]=1 в противном случае.
Массив ОТЕЦ описан ранее. Понятно, что он имеет длину n, где n — число вершин в графе.
В множестве Т будем хранить дуги ПВГ-деревьев.

Слайд 85Поиск в глубину



На следующем рис. показано,
как поиск в глубину

исследует неориентированный граф G. Предполагается, что в списках смежности этого графа вершины встречаются в порядке возрастания номеров, и, что цикл в строках 11-14 алгоритма Поиск в глубину.1 выполнялся в порядке возрастания номеров вершин.

Слайд 86Поиск в глубину



Слайд 87Поиск в глубину



В просмотренном графе G дуги
ПВГ-деревьев обозначены стрелками

в соответствии с ориентацией, полученной в ходе поиска.
Такие дуги часто называют прямыми дугами поиска. Прочие ребра графа, называемые иногда обратными дугами поиска, обозначены на рисунке пунктирами.
Числа в скобках, стоящие у вершин просмотренного графа, соответствуют очередности, в которой они просматривались в ходе поиска.
Отметим, что вершины с номерами 1, 9 и 11 являются корнями ПВГ-деревьев.

Слайд 88Поиск в глубину



Разберем теперь нерекурсивную версию процедуры ПВГ(v).
Рекурсия устраняется

стандартным способом с помощью стека.
Каждая вершина помещается в стек сразу, как только будет достигнута, то есть просмотрена, и удаляется из стека после того, как будет использована.
Поиск новой непросмотренной вершины ведется из той вершины, которая последней попала в стек.

Слайд 89Поиск в глубину



Для организации такого процесса понадобится дополнительно массив указателей


УКАЗ длины n, где n=|V|.
Предполагается, что в начале работы процедуры поиска выполняются равенства УKA3[v]=HAЧAЛO[v], для всех v из V, иначе говоря, УКАЗ[v] дает адрес первой записи в списке ЗАПИСЬ[v].
В процессе работы процедуры поиска УКАЗ[v] меняется таким образом, что указывает на следующую запись в списке ЗАПИСЬ[v] после той, которая содержит последнюю просмотренную из нее вершину.

Слайд 90Поиск в глубину



procedure ПВГ1(v); (* нерекурсивная

версия *)
begin
СТЕК :=Ø; СТЕК v; METKA[v]:=l;
while СТЕК ≠ Ø do
begin u СТЕК;
while (УКАЗ[u] ≠ nil) and (МЕТКА[УКАЗ[u]^.строка]=1) do
УКАЗ[u] := УКАЗ[u]^.след;
if УКАЗ[u] ≠ nil then (*найдена непросмотренная вершина *)
begin w := УКАЗ[u]^.строка:
СТЕК w; OTEЦ[w]:=u; METKA[w]:=l;
T := T(u,w); УКАЗ[u]:= УКАЗ[u]^.след;
end;
else СТЕК (* вершина u использована *)
end;
end.

Слайд 91Поиск в глубину



Теорема.
Сложность алгоритма
Поиск в глубину 1 есть

O(n+m).

Следствие.
Связные компоненты неориентированного графа могут быть найдены за время O(n+m).

Слайд 92Поиск в глубину



Поиск в глубину в ориентированном графе отличается от

поиска в неориентированном графе только тем, что ребра проходятся в соответствии с их ориентацией.
Поскольку в главе 2 мы условились считать, что в списке ЗАПИСЬ[у] встречаются только те вершины w,
для которых (v,w) E,
то алгоритм Поиск в глубину1 корректно работает и в ориентированных графах.


Слайд 93Поиск в ширину



Поиск в ширину
Другое название этого популярнейшего метода

— волновой алгоритм.
Причины появления такого названия станут ясны из дальнейшего.
Поиск в ширину начинается с некоторой фиксированной вершины v, называемой корнем.
Вершину v считаем просмотренной и помещаем ее в организуемую нами очередь.
Считаем также, что вершина v образует нулевой фронт распространения волны.


Слайд 94Поиск в ширину



Затем проходим все ребра {v,w}, инцидентные v, в

каком-нибудь порядке и ориентируем их из v в w.
Вершины w, смежные с v, считаем просмотренными
и размещаем их в порядке просмотра ребер в очередь.
Для всех таких вершин w полагаем
OTEЦ [w]:=v и говорим, что w просмотрена из v.
Ориентированные ребра (v,w) будем называть ребрами ПВШ(v)-дерева.
Говорят часто, что все такие вершины w образуют первый фронт распространения волны.
Вершина v после этих действий считается использованной и удаляется из очереди.


Слайд 95Поиск в ширину



Дальнейший поиск продолжается следующим образом. Берем очередную вершину

v из очереди, проходим по всем ребрам, ин­цидентным v, которые соединяют вершину v с еще непросмотренными вершинами w.
Все такие вершины w объявляются просмотренными, для них
полагают OTEЦ[w]:=v, ребра (v,w) относят к ПВШ(v)-дереву.


Слайд 96Поиск в ширину



После этих действий вершина v считается использованной и

удаляется из очереди. Говорят также, что вершины, просмотренные из вершин, принадлежащих фронту с номером k,
образуют (k+1)-ый фронт распространения волны.
Завершается поиск в ширину с корнем в заданной вершине таким же образом, как и поиск в глубину, а именно тогда, когда ни одной новой вершины просмотреть не удается.


Слайд 97Поиск в ширину



На следующем рисунке (2) показано, как поиск в

ширину исследует граф G, изображенный ранее на рис. (1).
Дуги ПВШ-деревьев изображены стрелками в соответствии с ориентацией, полученной в ходе поиска. Прочие ребра исходного графа изображены пунктиром.
Предполагалось, что вершины в ходе поиска просматривались в порядке возрастания их номеров.


Слайд 98Поиск в ширину




Слайд 99Поиск в ширину



Отметим, что в ПВШ(1) - дереве поиска вершины

2, 3, 4 обра­зуют первый фронт распространения волны, вершины 5, 6 и 7 — второй, а вершина 8 — третий.


Слайд 100Поиск в ширину



Отметим, что в ПВШ(1) –
дереве поиска вершины

2, 3, 4 образуют первый фронт распространения волны,
вершины 5, 6 и 7 — второй,
а вершина 8 — третий.
Далее представлен
АЛГОРИТМ 4.2. ПОИСК В ШИРИНУ
Данные: неориентированный граф G=(V,E), заданный списками смежностей.
Результаты: массив ОТЕЦ, множество D.


Слайд 101Поиск в ширину



procedure ПВШ(v); (* поиск в ширину с корнем v

*)
begin ОЧЕРЕДЬ :=Ø; ОЧЕРЕДЬ v; METKA[v]:=1;
while ОЧЕРЕДЬ ≠Ø do
begin u ОЧЕРЕДЬ; ОЧЕРЕДЬ;
for w ЗАПИСЬ[u] do (* используем вершину u *)
if METKA[w]=0 then
begin ОЧЕРЕДЬ w; OTEЦ[w]:=u; METKA[w]:=1;
D=Du{(u,w)};
end;
end;
end;
begin (*главная программа*)
D:=Ø; for vV do METKA[v]:=0; (* инициализация *)
for v V do
if METKA[v]=0 then (*v – корень*)
begin OTEЦ([v]:=nil; ПВШ(v);
end;
end.


Слайд 102Поиск в ширину



В приведенном формальном описании алгоритма поиска в ширину

переменная МЕТКА имеет тот же смысл, что и ранее в алгоритме Поиск в глубину 1.
Дуги ПВШ-деревьев хранятся в множестве D.
Смысл переменной ОТЕЦ объяснен выше. Просмотренные вершины помещаются в ОЧЕРЕДЬ и удаляются оттуда сразу после их использования (строка 4 алгоритма).


Слайд 103Поиск в ширину



В алгоритме Поиск в ширину 2 связность графа

не предполагается. Для корневых вершин поиска и только для них выполняется равенство ОТЕЦ[v]=nil.
Теорема 4.2. Алгоритм ПОИСК В ШИРИНУ 2 имеет вычислительную сложность O(n+m).


Слайд 104Цепи и пути в графах



Применительно к только связным неориентированным графам

нетрудно проверить, что и ПВГ-дерево, и ПВШ-дерево действительно являются деревьями, и более того — корневыми деревьями, причем корнями этих деревьев являются те вершины, с которых начинался поиск
(собственно поэтому они и в ПВГ и в ПВШ названы корневыми вершинами).


Слайд 105Цепи и пути в графах



Если в ориентированном графе имеется дуга

(v,w), то v — отец w, a w — сын v. Легко видеть, что даваемые алгоритмами ПоискВглубину1 и ПоискВширину2 значения переменных ОТЕЦ[w] согласуются с ранее введенным понятием, а именно, если v=ОТЕЦ[w], то (v,w)E.
Вершина v называется предком вершины w, и, соответственно, w — потомком v, если в корневом дереве существует путь от v до w. Например, в корневом дереве ПВШ(1)
из рис. вершина 8 является потомком вершины 2.


Слайд 106Цепи и пути в графах



Теорема 3. Пусть Т — ПВГ-дерево

связного неориентиро­ванного графа G=(V,E), и пусть {u,w}E. Тогда либо u — потомок w, либо w потомок u в корневом дереве Т.
Понятно, что ПВШ-дерево не обладает свойством, сформули­рованным в теореме3.
Например, в ПВШ(1)-дереве, изобра­женном на рис. 2, ни вершина 3 не является потомком вершины 6, ни вершина 6 не является потомком вершины 3
(говорят, что такие вершины несравнимы в корневом дереве).


Слайд 107Цепи и пути в графах



Как в ПВГ-дереве, так и в

ПВШ-дереве для каждой вершины w,
существует единственный путь из корня v в w.
Как построить этот путь?
Это несложно делается с помощью массива ОТЕЦ.
Отметим только, что под путем в орграфе мы договорились понимать в зависимости от степени удобства,
либо последовательность ребер, либо последовательность вершин.


Слайд 108Цепи и пути в графах



В предлагаемом ниже алгоритме ПостроениеПути3 требуемый

путь идентифицируется последовательностью вершин. Предполагается, что перед работой этого алгоритма работала либо процедура ПВГ(v), либо процедура ПВШ(v).


Слайд 109Цепи и пути в графах



АЛГОРИТМ ПостроениеПути3.
Данные: корневая вершина поиска

v, вершина w. массив ОТЕЦ.
begin
СТЕК:=Ø; СТЕК w; u:=w;
while u≠v do
begin u:=ОТЕЦ[u];
CTEK u;
end;
end.
Результат: СТЕК, содержащий последовательность вершин, об­разующих v-w-путь.


Слайд 110Цепи и пути в графах



Понятно, что последовательность вершин v=v0,v1,...,vk=w, по­лученная

считыванием СТЕКА, образует как v-w-путь в корневом дереве Т (или D), так и v-w-цепь в исходном графе G.
Оказывается, что пути, построенные поиском в ширину, обладают очень полезным свойством, а именно, справедлива.
Теорема 4. Пусть D — ПВШ-дерево с корнем v связного неориентированного графа G=(V,E).
Тогда для любой вершины w V единственный v-w-путь в D определяет кратчайшую по числу ребер цепь среди всех v-w-цепей в графе G.



Слайд 111Цепи и пути в графах



Заметим, что пути, определяемые поиском в

глубину, вообще говоря, не являются кратчайшими. Например, на рис.1 путь от вершины 1 до вершины 8 проходит через вершины 2,3,4,7,6 и имеет длину 6, а поиск в ширину (см.рис.2) определяет путь, проходящий через вершины 4,7, длиной 3.



Похожие презентации

Правила сложения и умножения вероятностей и их следствия 480
urok 5 234
Пирамида. Элементы пирамиды 448
uud matematika 240
Эконометрика. Элементы теории вероятностей и математической статистики. (Тема 1) 459
Нумерация в концентре 1000 273

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика