- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Платоновы тела. Правильные многрграники презентация
Содержание
- 1. Платоновы тела. Правильные многрграники
- 2. Основные понятия Многогранник - это геометрическое
- 3. Многогранник называется выпуклым, если он весь расположен
- 4. Правильные многогранники Тетра́эдр (др.-греч. τετρά-εδρον — четырёхгранник)
- 5. Правильные многогранники Куб (др.-греч. κύβος) (иногда гекса́эдр
- 6. Правильные многогранники Октаэдр (греч. οκτάεδρον, от греч.
- 7. Правильные многогранники Додека́эдр (от др.-греч. δώδεκα —
- 8. Правильные многогранники Икоса́эдр (от др.-греч. εἴκοσι «двадцать»;
- 9. Историческая справка Правильные многогранники известны с древнейших
Слайд 2Основные понятия
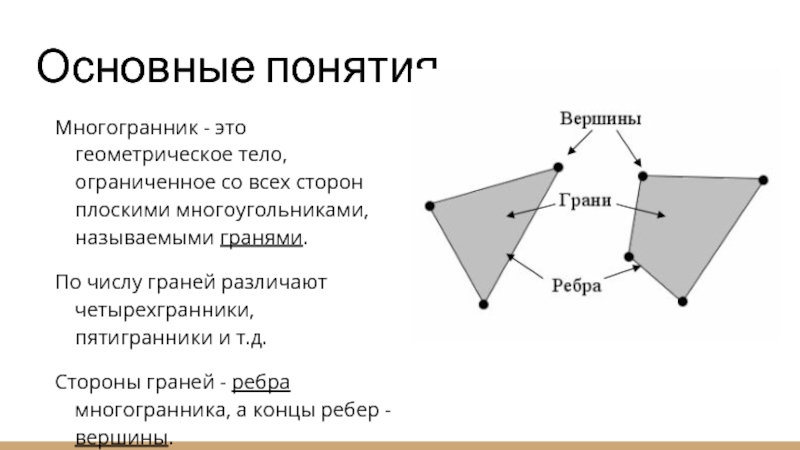
Многогранник - это геометрическое тело, ограниченное со всех сторон
плоскими многоугольниками, называемыми гранями.
По числу граней различают четырехгранники, пятигранники и т.д.
Стороны граней - ребра многогранника, а концы ребер - вершины.
По числу граней различают четырехгранники, пятигранники и т.д.
Стороны граней - ребра многогранника, а концы ребер - вершины.
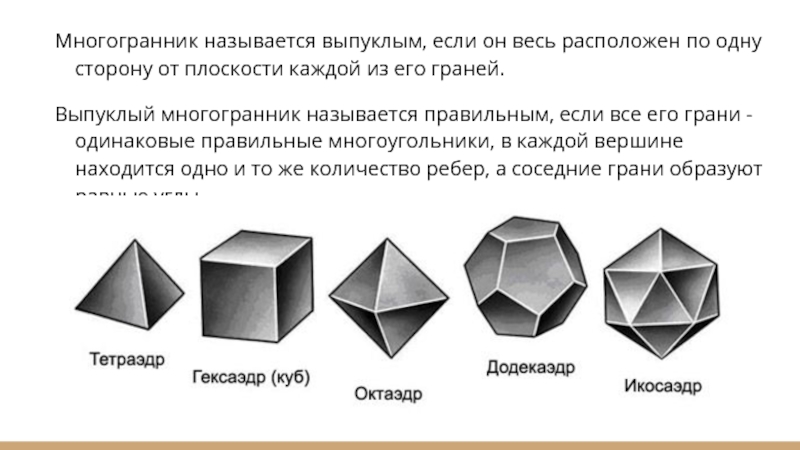
Слайд 3Многогранник называется выпуклым, если он весь расположен по одну сторону от
плоскости каждой из его граней.
Выпуклый многогранник называется правильным, если все его грани - одинаковые правильные многоугольники, в каждой вершине находится одно и то же количество ребер, а соседние грани образуют равные углы.
Правильных многогранников всего пять.
Выпуклый многогранник называется правильным, если все его грани - одинаковые правильные многоугольники, в каждой вершине находится одно и то же количество ребер, а соседние грани образуют равные углы.
Правильных многогранников всего пять.
Слайд 4Правильные многогранники
Тетра́эдр (др.-греч. τετρά-εδρον — четырёхгранник) - простейший многогранник, гранями которого
являются четыре треугольника[2], треугольная пирамида. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.
Слайд 5Правильные многогранники
Куб (др.-греч. κύβος) (иногда гекса́эдр или правильный гекса́эдр]) — правильный
многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Слайд 6Правильные многогранники
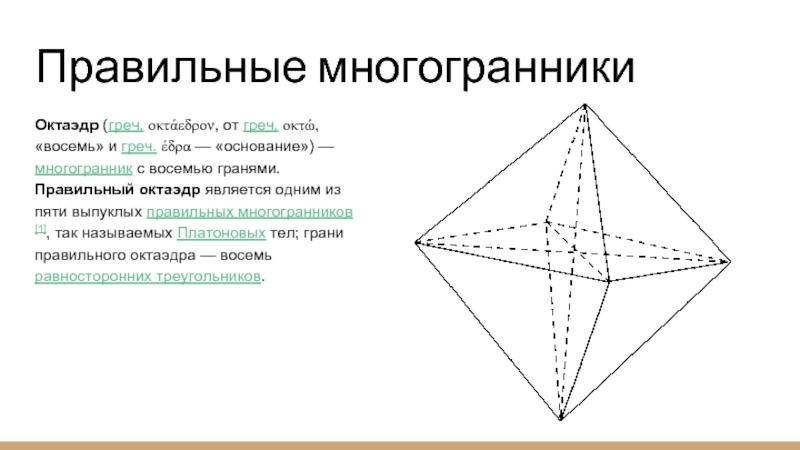
Октаэдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα
— «основание») — многогранник с восемью гранями. Правильный октаэдр является одним из пяти выпуклых правильных многогранников[1], так называемых Платоновых тел; грани правильного октаэдра — восемь равносторонних треугольников.
Слайд 7Правильные многогранники
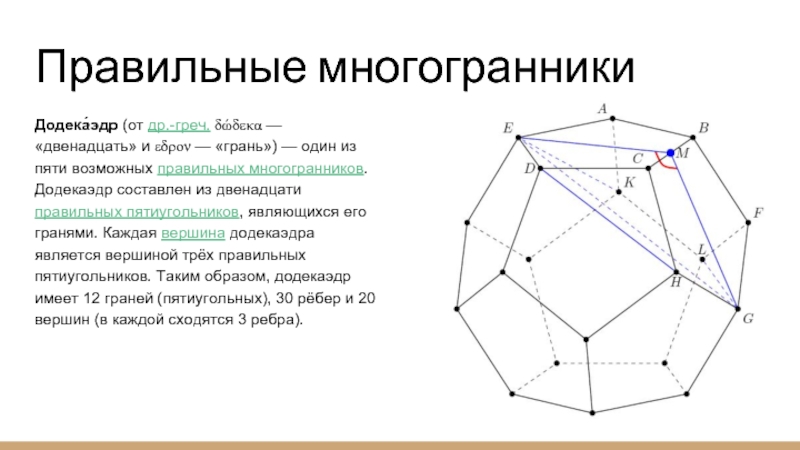
Додека́эдр (от др.-греч. δώδεκα — «двенадцать» и εδρον — «грань»)
— один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников, являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Слайд 8Правильные многогранники
Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный
выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Слайд 9Историческая справка
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно
найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

![Правильные многогранникиТетра́эдр (др.-греч. τετρά-εδρον — четырёхгранник) - простейший многогранник, гранями которого являются четыре треугольника[2], треугольная](/img/tmb/3/230164/9fc5f0fa9c1dfe29cca4f7706fc0f7e2-800x.jpg)
![Правильные многогранникиКуб (др.-греч. κύβος) (иногда гекса́эдр или правильный гекса́эдр]) — правильный многогранник, каждая грань которого](/img/tmb/3/230164/39a484247d226c42a0fbb796f0961fc4-800x.jpg)