- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пирамида. Задачи ЕГЭ презентация
Содержание
- 1. Пирамида. Задачи ЕГЭ
- 2. 1. Пересечение диагоналей параллелепипеда является его:
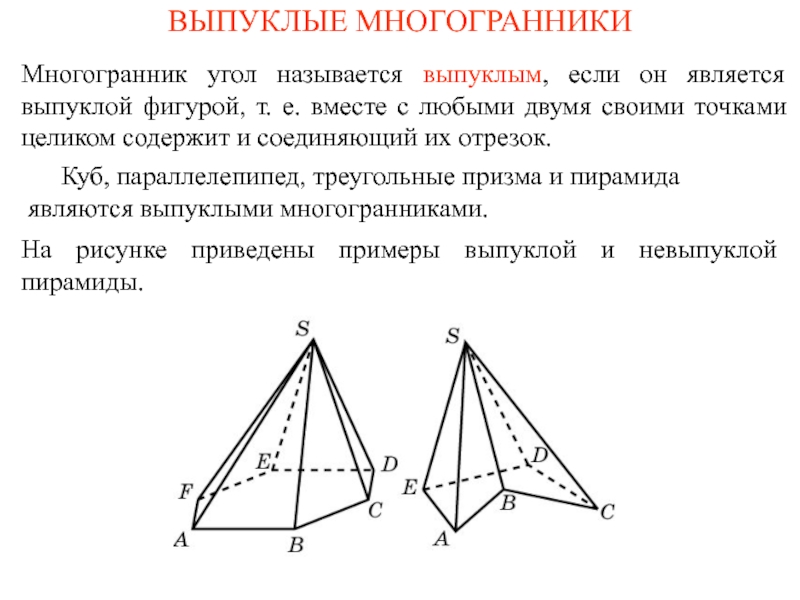
- 3. 2. Многогранник, который состоит из плоского многоугольника,
- 4. 3. Точки, не лежащие в плоскости основания пирамиды,
- 5. 4. Перпендикуляр, опущенный из вершины пирамиды на плоскость
- 6. 5. Отрезки, соединяющие вершину пирамиды с вершинами основания,
- 7. 6. К правильным многогранникам не относится: А) куб; Б) икосаэдр; В) тетраэдр; Г) пирамида.
- 8. 7. Отрезок, соединяющий две вершины призмы, не принадлежащие
- 9. 8. К многогранникам относятся: А) параллелепипед; Б) призма; В) пирамида; Г) все ответы верны.
- 10. 9. Если в основании призмы лежит параллелограмм, то
- 11. 10. Тело, поверхность которого состоит из конечного числа
- 12. 11. У призмы боковые ребра: А) равны;
- 13. 12. Грани параллелепипеда не имеющие общих вершин, называются:
- 14. 13. Боковая поверхность призмы состоит из: А) параллелограммов;
- 15. 14. Если боковые ребра призмы перпендикулярны основанию, то
- 16. 15. Высота боковой грани правильной пирамиды, проведенная из
- 17. Задание 1 Если каждое ребро куба
- 18. Задание 2 Основанием прямой треугольной призмы служит
- 19. Задание 3 В правильной треугольной пирамиде боковое
- 20. Задание 4 Найдите площадь поверхности правильной
- 21. Задание 5 Стороны основания правильной шестиугольной пирамиды
- 22. Задание 6 Во сколько раз увеличится
- 23. Задание 7 В правильной четырехугольной пирамиде SABCD
- 24. Задание 8 Во сколько раз увеличится
- 25. Задание 9 В правильной четырёхугольной пирамиде SABCD
- 26. Задание 10 В правильной треугольной пирамиде SABC
- 27. Задание 11 Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
- 28. Задание 12 В правильной треугольной пирамиде
- 29. Задание 13 В правильной треугольной пирамиде SABC
- 30. Задание 14 Во сколько раз увеличится
- 31. Задание 15 В правильной четырёхугольной пирамиде
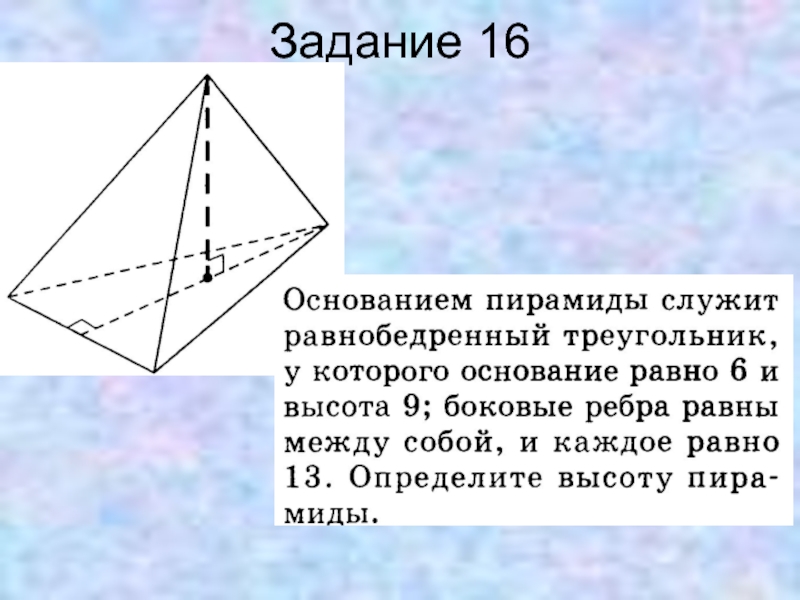
- 32. Задание 16
- 33. Задание 17 В правильной треугольной пирамиде
- 34. Задание 18 В правильной четырехугольной пирамиде SABCD
- 35. Задание 19 Стороны основания правильной шестиугольной пирамиды
- 36. Задание 20 В правильной четырехугольной пирамиде SABCD
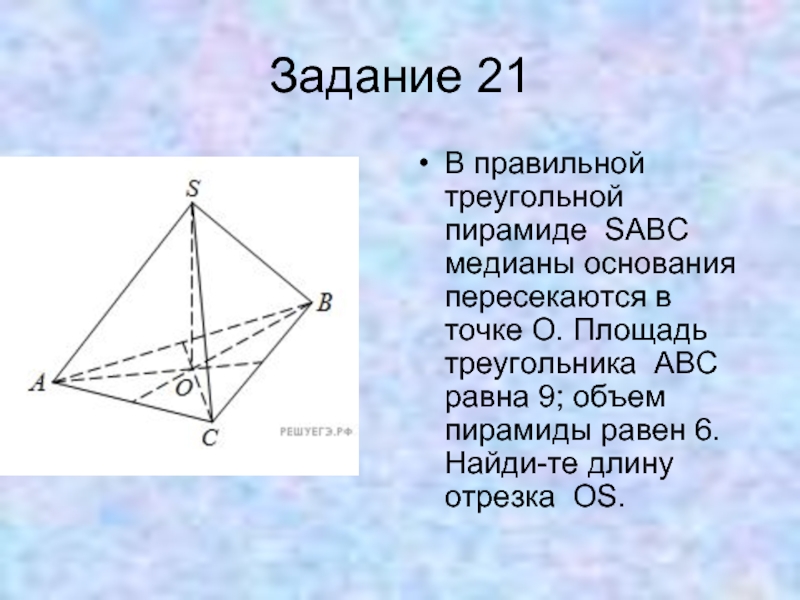
- 37. Задание 21 В правильной треугольной пирамиде SABC
Слайд 21. Пересечение диагоналей параллелепипеда является его:
А) центром;
Б) центром симметрии;
В) линейным размером;
Г) точкой сечения.
Слайд 3 2. Многогранник, который состоит из плоского многоугольника, точки и отрезков соединяющих
их, называется:
А) конусом;
Б) пирамидой;
В) призмой;
Г) шаром.
А) конусом;
Б) пирамидой;
В) призмой;
Г) шаром.
Слайд 43. Точки, не лежащие в плоскости основания пирамиды, называются:
А) вершиной пирамиды ;
Б)
боковыми ребрами;
В) линейным размером;
Г) вершинами грани.
В) линейным размером;
Г) вершинами грани.
Слайд 54. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:
А) медианой;
Б)
осью;
В) диагональю;
Г) высотой.
В) диагональю;
Г) высотой.
Слайд 65. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются:
А) гранями;
Б) сторонами;
В) боковыми
ребрами;
Г) диагоналями.
Г) диагоналями.
Слайд 87. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
А) диагональю;
Б) ребром;
В) осью;
Г) гранью.
Слайд 109. Если в основании призмы лежит параллелограмм, то она является:
А) правильной призмой;
Б) параллелепипедом;
В) правильным многоугольником;
Г) пирамидой.
Слайд 1110. Тело, поверхность которого состоит из конечного числа плоских многоугольников, называется:
А) четырехугольник;
Б) многоугольник;
В) многогранник;
Г) шестиугольник.
Слайд 1211. У призмы боковые ребра:
А) равны;
Б) симметричны;
В) параллельны и равны;
Г) параллельны.
Слайд 1312. Грани параллелепипеда не имеющие общих вершин, называются:
А) противолежащими;
Б) противоположными;
В) симметричными;
Г) равными.
Слайд 1413. Боковая поверхность призмы состоит из:
А) параллелограммов;
Б) квадратов;
В) ромбов;
Г) треугольников.
Слайд 1514. Если боковые ребра призмы перпендикулярны основанию, то призма является:
А) наклонной;
Б)
правильной;
В) прямой;
Г) выпуклой.
В) прямой;
Г) выпуклой.
Слайд 1615. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется:
А) медианой;
Б) апофемой;
В) биссектрисой;
Г) высотой.
Слайд 17Задание 1
Если каждое ребро куба увеличить на 1, то его объем
увеличится на 919. Найдите ребро куба.
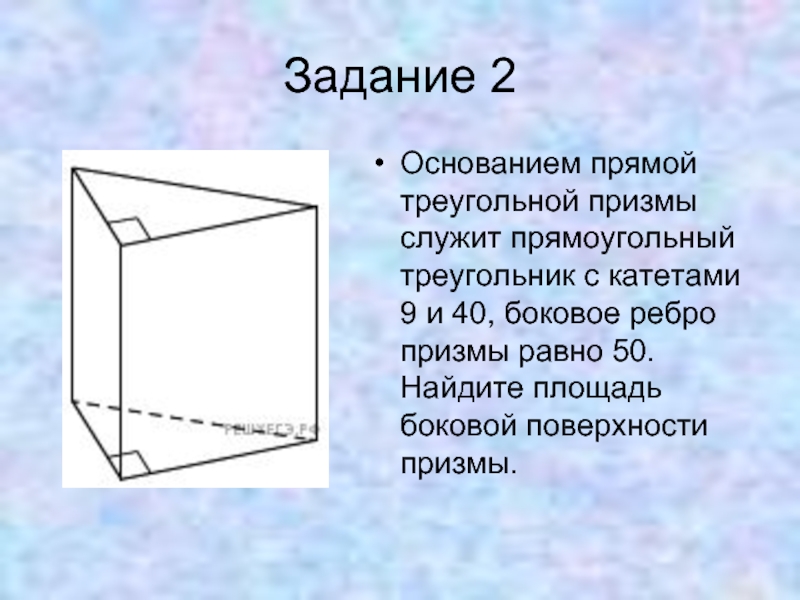
Слайд 18Задание 2
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9
и 40, боковое ребро призмы равно 50. Найдите площадь боковой поверхности призмы.
Слайд 19Задание 3
В правильной треугольной пирамиде боковое ребро равно 5, а тангенс
угла между боковой гранью и плоскостью основания равен 0,25√11. Найти сторону основания пирамиды.
Слайд 20Задание 4
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны
48 и высота равна 7.
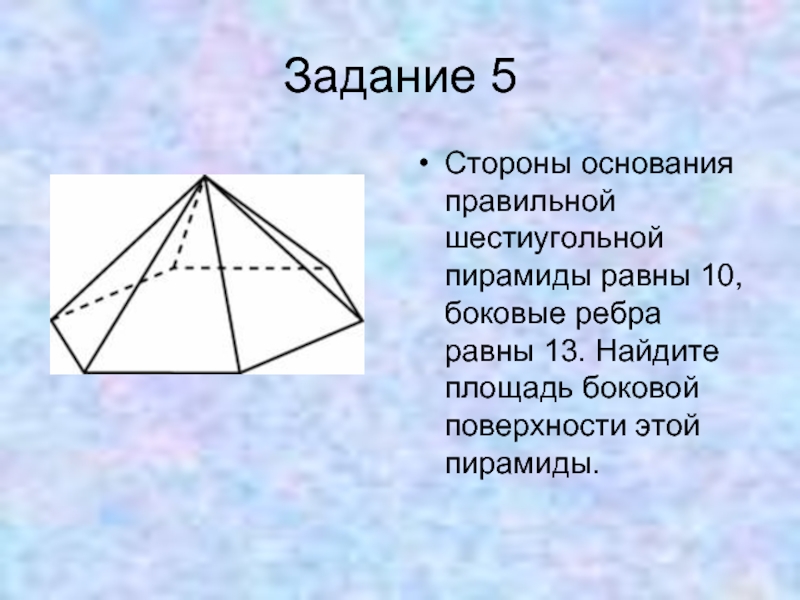
Слайд 21Задание 5
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны
13. Найдите площадь боковой поверхности этой пирамиды.
Слайд 22Задание 6
Во сколько раз увеличится площадь поверхности октаэдра, если все его
ребра увеличить в 22 раза?
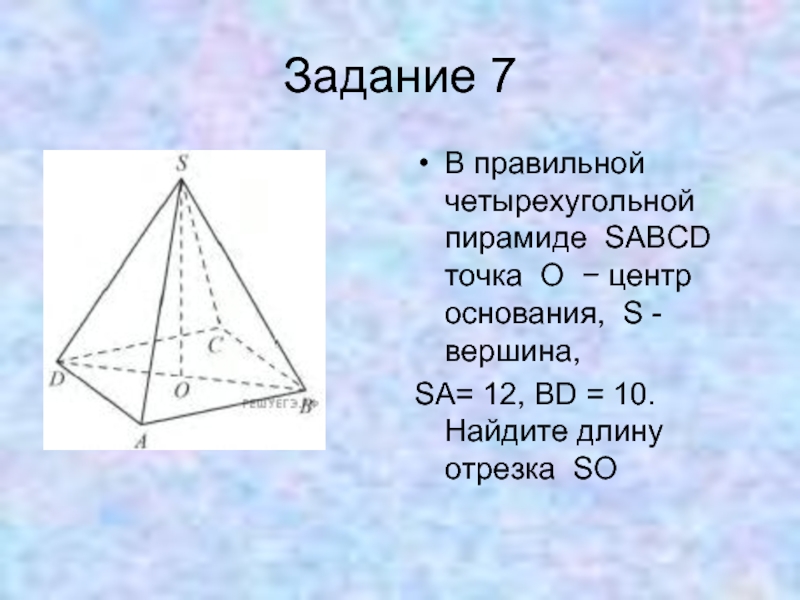
Слайд 23Задание 7
В правильной четырехугольной пирамиде SABCD точка O − центр основания,
S - вершина,
SA= 12, BD = 10. Найдите длину отрезка SO
SA= 12, BD = 10. Найдите длину отрезка SO
Слайд 24Задание 8
Во сколько раз увеличится площадь поверхности пирамиды, если все ее
ребра увеличить в 3 раза?
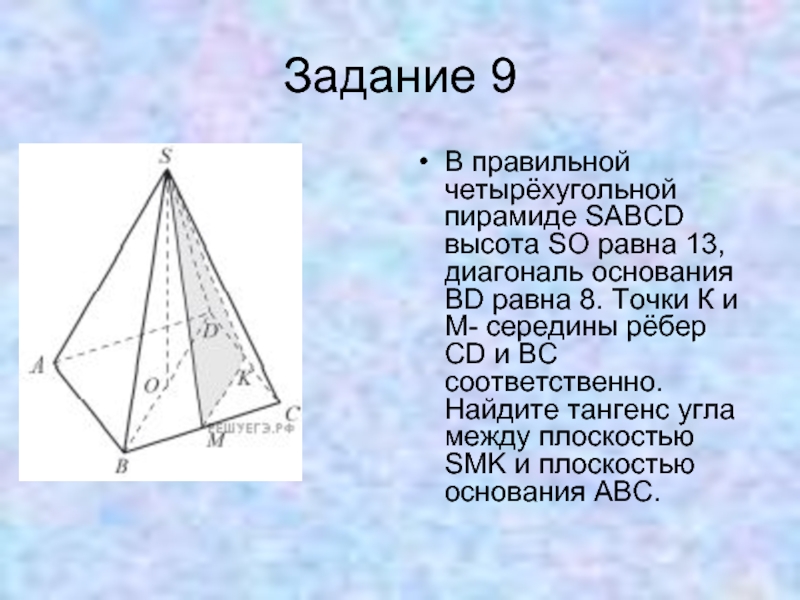
Слайд 25Задание 9
В правильной четырёхугольной пирамиде SABCD высота SO равна 13, диагональ
основания BD равна 8. Точки К и М- середины рёбер CD и ВС соответственно. Найдите тангенс угла между плоскостью SMK и плоскостью основания ABC.
Слайд 26Задание 10
В правильной треугольной пирамиде SABC точка M – середина ребра
AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
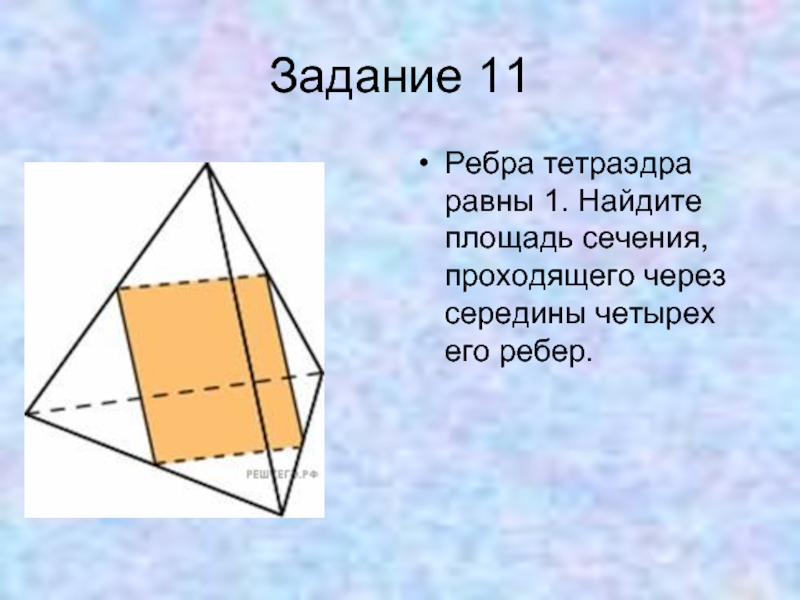
Слайд 27Задание 11
Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины
четырех его ребер.
Слайд 28Задание 12
В правильной треугольной пирамиде SABC точка Q — середина ребра
AB, S— вершина. Известно, что BC =5 , а площадь боковой поверхности равна 45. Найдите длину отрезка SQ.
Слайд 29Задание 13
В правильной треугольной пирамиде SABC точка L — середина ребра
AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды
Слайд 30Задание 14
Во сколько раз увеличится площадь поверхности пирамиды, если все ее
ребра увеличить в 3 раза?
Слайд 31Задание 15
В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс
угла между боковой гранью и плоскостью основания равен √14 Найти сторону основания пирамиды.
Слайд 33Задание 17
В правильной треугольной пирамиде SABC Q
– середина ребра AB, S – вершина. Известно, что BC =7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка SQ.
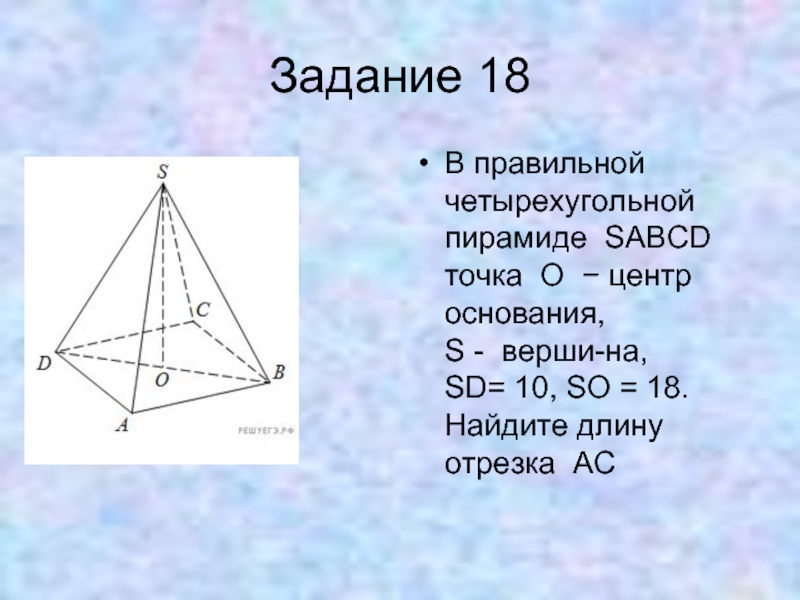
Слайд 34Задание 18
В правильной четырехугольной пирамиде SABCD точка O − центр основания,
S - вершина, SD= 10, SO = 18. Найдите длину отрезка AC
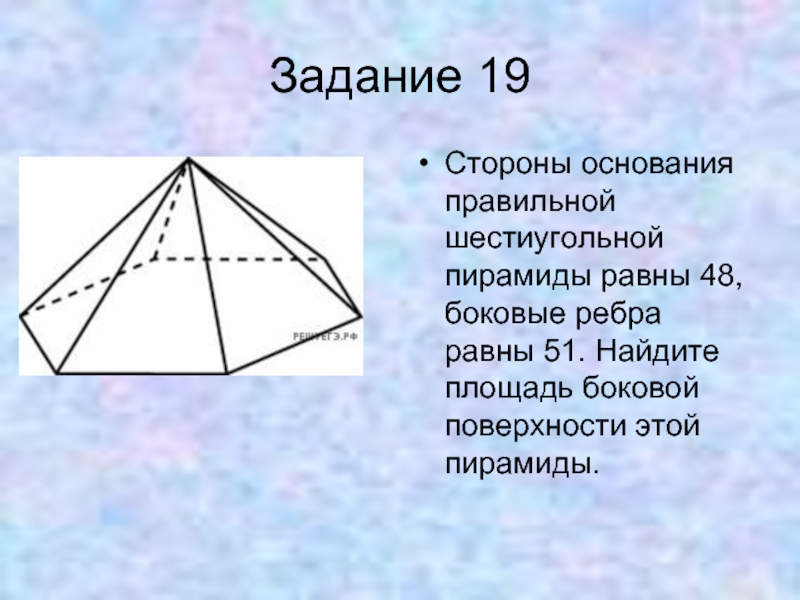
Слайд 35Задание 19
Стороны основания правильной шестиугольной пирамиды равны 48, боковые ребра равны
51. Найдите площадь боковой поверхности этой пирамиды.
Слайд 36Задание 20
В правильной четырехугольной пирамиде SABCD точка O − центр основания,
S -вершина,
SO= 12, BD = 18. Найдите длину отрезка SA
SO= 12, BD = 18. Найдите длину отрезка SA
Слайд 37Задание 21
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке
O. Площадь треугольника ABC равна 9; объем пирамиды равен 6. Найдите длину отрезка OS.