- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Парная линейная регрессия и метод наименьших квадратов презентация
Содержание
- 1. Парная линейная регрессия и метод наименьших квадратов
- 2. Цели лекции Раскрыть понятие регрессии. Познакомиться
- 3. Виды зависимостей между переменными 1. Функциональные: Y
- 4. Виды статистических зависимостей а) Корреляционные: при изменении
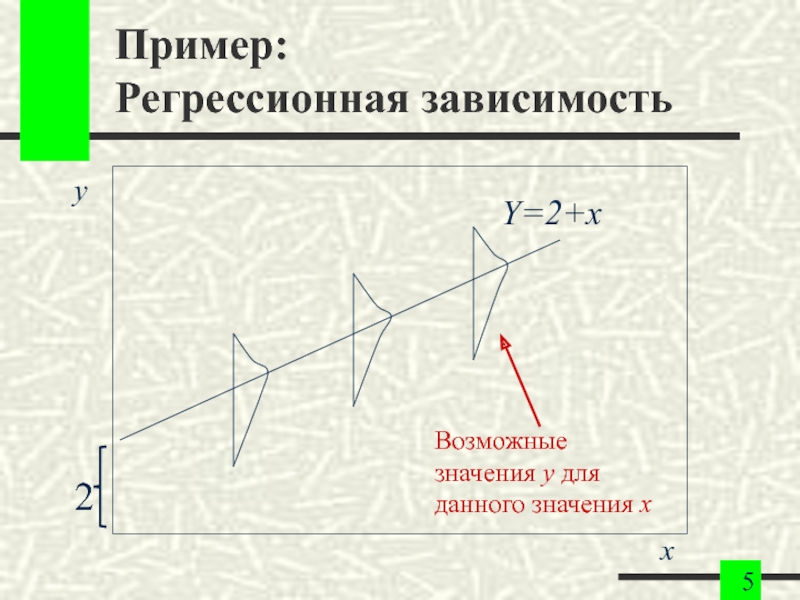
- 5. Пример: Регрессионная зависимость y
- 6. Что такое регрессионный анализ? Регрессионный анализ –
- 7. Определение регрессии Регрессия – функциональная зависимость между
- 8. Регрессионные модели Mx[Y] = ϕ(X) − парная
- 9. Пример: Парная регрессия Мы хотим определить зависимость
- 10. Пример: Множественная регрессия Мы хотим определить связь
- 11. Регрессионные уравнения Y = M[Y/x] + ε
- 12. Причины обязательного присутствия случайного фактора Невключение
- 13. Этапы построения качественного уравнения регрессии 1.
- 14. Этапы построения качественного уравнения регрессии 4.
- 15. Выбор формы парной регрессии В случае парной
- 16. Примеры взаимосвязи между переменными а) Взаимосвязь между
- 17. Парная линейная регрессия Модель линейной регрессии является
- 18. Модель Кейнса Рассмотрим модель Кейнса зависимости частного
- 19. Модель парной линейной регрессии Теоретическая парная линейная
- 20. Задачи линейного регрессионного анализа Задачи линейного регрессионного
- 21. Эмпирическое уравнение регрессии По выборке ограниченного объема
- 22. Эмпирическое уравнение регрессии В результате имеем:
- 23. Эмпирическое и теоретическое уравнения регрессии Соотношение между
- 24. Задача определения коэффициентов регрессии Задача состоит в
- 25. Метод наименьших квадратов Наиболее распространена методом наименьших
- 26. Метод наименьших квадратов Пусть по выборке данных
- 27. Метод наименьших квадратов В этом случае минимизируется
- 28. Метод наименьших квадратов Приравняем нулю частные производные и затем разделим на n оба уравнения:
- 29. Оценки метода наименьших квадратов Решив последнюю систему уравнений, получим:
- 30. Матричная форма записи МНК эквивалентен ортогональности матрицы Х и вектора е:
- 31. Выводы 1. Оценки МНК являются
- 32. Выводы 4. Эмпирическое уравнение регрессии построено
- 33. Другие методы определения коэффициентов регрессии Другие методы
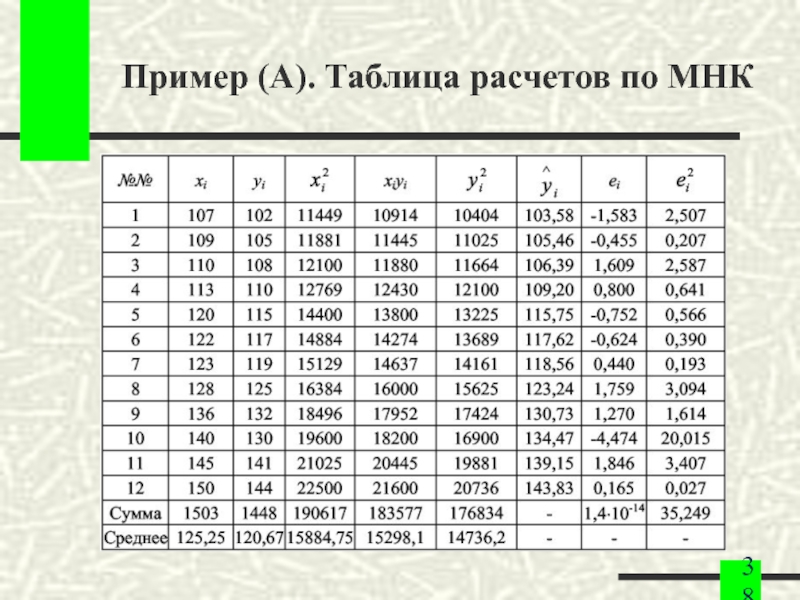
- 34. Пример (A) построения уравнения регрессии При анализе
- 35. Пример (A) построения уравнения регрессии Для определения
- 36. Пример (A) построения уравнения регрессии По расположению
- 37. Пример (A) построения уравнения регрессии Т.о., уравнение
- 38. Пример (A). Таблица расчетов по МНК
- 39. Конец лекции
Слайд 2Цели лекции
Раскрыть понятие регрессии.
Познакомиться с методом наименьших квадратов – методом построения
линейного уравнения регрессии.
Слайд 3Виды зависимостей между переменными
1. Функциональные: Y = f(X).
Имеют место при исследовании
связей между
неслучайными переменными. Такие связи в
эконометрике не рассматриваются.
2. Статистические: изменение одной из величин влечет изменение закона распределения другой (доход – потребление, цена – спрос и т.д.).
неслучайными переменными. Такие связи в
эконометрике не рассматриваются.
2. Статистические: изменение одной из величин влечет изменение закона распределения другой (доход – потребление, цена – спрос и т.д.).
Слайд 4Виды статистических зависимостей
а) Корреляционные: при изменении одной из величин изменяется среднее
значение другой (связь между переменными не носит направленного характера)
M[Y/X = x] = Mx[Y] = ϕ(x), M[X/Y = y] = My[X] = ψ(y),
где M[Y/X = x] − м. о. случайной величины Y, вычисленное при условии, что случайная величина X приняла значение x, ϕ(x) ≠ const, ψ(y) ≠ const.
б) Регрессионные: односторонняя зависимость среднего значения случайной величины Y от одной X или нескольких X1,…,Xm случайных величин.
M[Y/X = x] = Mx[Y] = ϕ(x), M[X/Y = y] = My[X] = ψ(y),
где M[Y/X = x] − м. о. случайной величины Y, вычисленное при условии, что случайная величина X приняла значение x, ϕ(x) ≠ const, ψ(y) ≠ const.
б) Регрессионные: односторонняя зависимость среднего значения случайной величины Y от одной X или нескольких X1,…,Xm случайных величин.
Слайд 6Что такое регрессионный анализ?
Регрессионный анализ – наиболее часто используемый инструмент в
эконометрике.
Регрессионный анализ представляет собой анализ форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого случайного процесса.
Регрессионный анализ представляет собой анализ форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого случайного процесса.
Слайд 7Определение регрессии
Регрессия – функциональная зависимость между объясняющими переменными и условным математическим
ожиданием (средним значением) зависимой переменной, которая строится с целью прогнозирования этого среднего значения при фиксированных значениях объясняющих переменных.
Слайд 8Регрессионные модели
Mx[Y] = ϕ(X) − парная регрессия,
Mx[Y] = ϕ(X1,…,Xm) − множественная
регрессия,
где ϕ(X) ≠ const,
X − объясняющая, входная, предсказывающая,
экзогенная, неслучайная переменная, фактор,
регрессор, факторный признак;
Y − зависимая, объясняемая, выходная,
результирующая, эндогенная, случайная
переменная, результирующий признак.
где ϕ(X) ≠ const,
X − объясняющая, входная, предсказывающая,
экзогенная, неслучайная переменная, фактор,
регрессор, факторный признак;
Y − зависимая, объясняемая, выходная,
результирующая, эндогенная, случайная
переменная, результирующий признак.
Слайд 9Пример:
Парная регрессия
Мы хотим определить зависимость между продажами и затратами на рекламу.
y
– продажи.
x – рекламные расходы.
x – рекламные расходы.
Слайд 10Пример:
Множественная регрессия
Мы хотим определить связь между потреблением, доходом семьи, финансовыми активами
семьи и размером семьи.
y – потребительские расходы.
x1 – доход семьи.
x2 – финансовые активы семьи.
x3 – размер семьи.
y – потребительские расходы.
x1 – доход семьи.
x2 – финансовые активы семьи.
x3 – размер семьи.
Слайд 11Регрессионные уравнения
Y = M[Y/x] + ε = ϕ(x) + ε −
уравнение парной регрессии,
Y = M[Y/x1 ,…, xm] + ε = ϕ(x1 ,…, xm) + ε − уравнение множественной регрессии,
где ε − случайный фактор (остаток), обусловленный многими причинами.
В зависимости от вида функции ϕ(x) модели делятся на линейные и нелинейные.
Y = M[Y/x1 ,…, xm] + ε = ϕ(x1 ,…, xm) + ε − уравнение множественной регрессии,
где ε − случайный фактор (остаток), обусловленный многими причинами.
В зависимости от вида функции ϕ(x) модели делятся на линейные и нелинейные.
Слайд 12Причины обязательного присутствия случайного фактора
Невключение в модель всех объясняющих переменных.
Неправильный выбор
функциональной формы модели.
Агрегирование переменных (факторы представляют собой комбинацию других переменных).
Ошибки измерений.
Ограниченность статистических данных.
Непредсказуемость человеческого фактора.
Агрегирование переменных (факторы представляют собой комбинацию других переменных).
Ошибки измерений.
Ограниченность статистических данных.
Непредсказуемость человеческого фактора.
Слайд 13Этапы построения качественного уравнения регрессии
1. Определение конечных целей эконометрического моделирования,
набора участвующих в модели факторов и их роли (постановочный этап).
2. Предмодельный анализ экономической сущности изучаемого явления (априорный этап).
3. Сбор необходимой статистической информации (информационный этап).
2. Предмодельный анализ экономической сущности изучаемого явления (априорный этап).
3. Сбор необходимой статистической информации (информационный этап).
Слайд 14Этапы построения качественного уравнения регрессии
4. Выбор формулы уравнения регрессии (спецификация
уравнения регрессии).
5. Определение параметров выбранного уравнения (параметризация).
6. Анализ качества уравнения и проверка его адекватности эмпирическим данным, совершенствование уравнения (верификация).
5. Определение параметров выбранного уравнения (параметризация).
6. Анализ качества уравнения и проверка его адекватности эмпирическим данным, совершенствование уравнения (верификация).
Слайд 15Выбор формы парной регрессии
В случае парной регрессии выбор формулы обычно осуществляется
по графическому изображению реальных статистических данных в виде точек (корреляционное поле или диаграмма рассеивания).
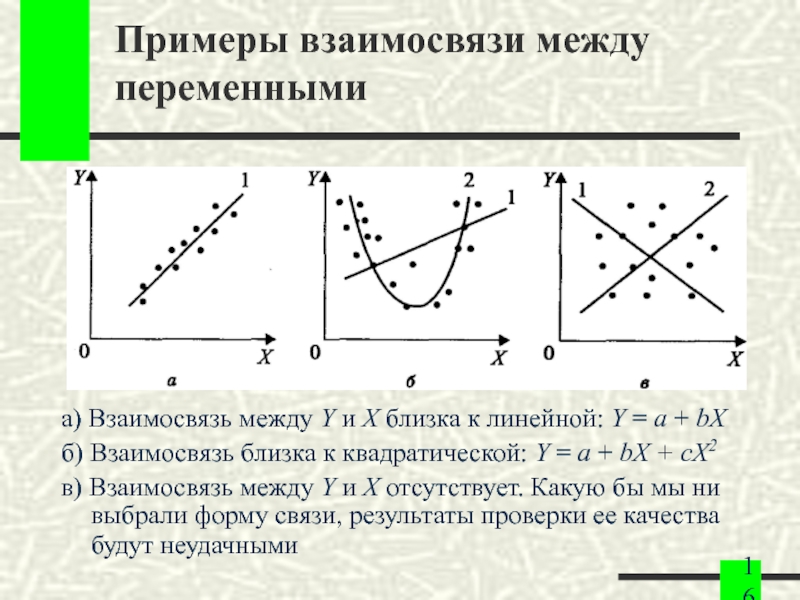
Слайд 16Примеры взаимосвязи между переменными
а) Взаимосвязь между Y и X близка к
линейной: Y = a + bX
б) Взаимосвязь близка к квадратической: Y = a + bX + cX2
в) Взаимосвязь между Y и X отсутствует. Какую бы мы ни выбрали форму связи, результаты проверки ее качества будут неудачными
б) Взаимосвязь близка к квадратической: Y = a + bX + cX2
в) Взаимосвязь между Y и X отсутствует. Какую бы мы ни выбрали форму связи, результаты проверки ее качества будут неудачными
Слайд 17Парная линейная регрессия
Модель линейной регрессии является
наиболее распространенной (и простой)
зависимостью между переменными,
а также
может служить начальной точкой
эконометрического анализа.
может служить начальной точкой
эконометрического анализа.
Слайд 18Модель Кейнса
Рассмотрим модель Кейнса зависимости частного
потребления С от располагаемого дохода I:
С = С0+bI,
где С0 − величина автономного потребления, b − предельная
склонность к потреблению (0 < b ≤ 1)
где С0 − величина автономного потребления, b − предельная
склонность к потреблению (0 < b ≤ 1)
Слайд 19Модель парной линейной регрессии
Теоретическая парная линейная регрессионная
модель:
где β0,
β1 − теоретические коэффициенты регрессии,
εi − случайное отклонение.
В общем виде теоретическую парную линейную
регрессионную модель будем представлять в виде:
εi − случайное отклонение.
В общем виде теоретическую парную линейную
регрессионную модель будем представлять в виде:
Слайд 20Задачи линейного регрессионного анализа
Задачи линейного регрессионного анализа состоят в
том, чтобы по
имеющимся статистическим данным
(xi, yi), i = 1, 2, …, n, для переменных X и Y:
а) получить наилучшие оценки параметров β0 и β1;
б) проверить статистические гипотезы о параметрах модели;
в) проверить, адекватность модели данным наблюдений.
(xi, yi), i = 1, 2, …, n, для переменных X и Y:
а) получить наилучшие оценки параметров β0 и β1;
б) проверить статистические гипотезы о параметрах модели;
в) проверить, адекватность модели данным наблюдений.
Слайд 21Эмпирическое уравнение регрессии
По выборке ограниченного объема нельзя точно
определить теоретические значения β0
и β1..
Можно лишь построить эмпирическое уравнение
регрессии:
где b0 и b1 – оценки параметров β0 и β1 эмпирические
коэффициенты регрессии).
– оценка условного м. о. M[Y/X = xi].
Можно лишь построить эмпирическое уравнение
регрессии:
где b0 и b1 – оценки параметров β0 и β1 эмпирические
коэффициенты регрессии).
– оценка условного м. о. M[Y/X = xi].
Слайд 22Эмпирическое уравнение регрессии
В результате имеем:
где ei – оценка теоретического
случайного отклонения εi .
Оценки b0 и b1 отличаются от истинных значений β0 и β1,
что приводит к несовпадению эмпирической и
теоретической линий регрессии. По различным
выборкам из одной и той же генеральной
совокупности получают разные значения оценок
коэффициентов регрессии.
Оценки b0 и b1 отличаются от истинных значений β0 и β1,
что приводит к несовпадению эмпирической и
теоретической линий регрессии. По различным
выборкам из одной и той же генеральной
совокупности получают разные значения оценок
коэффициентов регрессии.
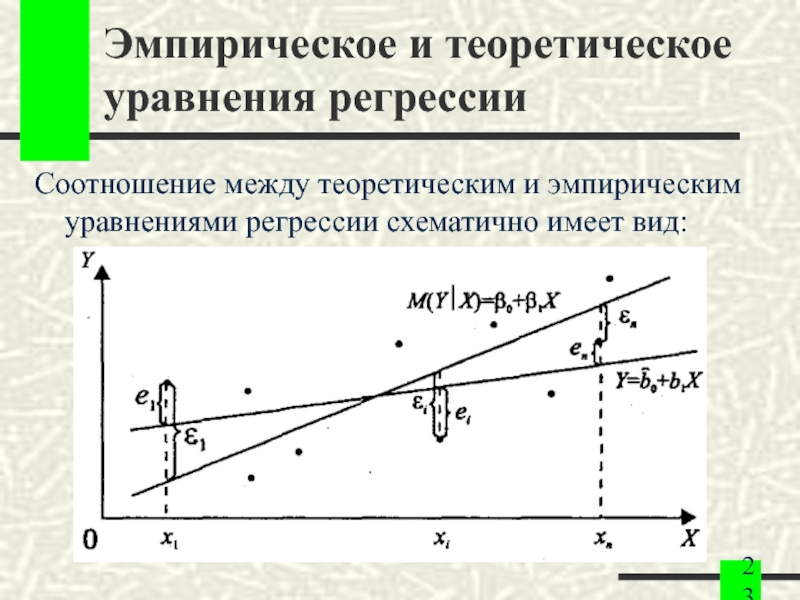
Слайд 23Эмпирическое и теоретическое уравнения регрессии
Соотношение между теоретическим и эмпирическим уравнениями регрессии
схематично имеет вид:
Слайд 24Задача определения коэффициентов регрессии
Задача состоит в нахождении по выборке данных
оценок b0
и b1 так, чтобы построенная линия регрессии
была наилучшей в определенном смысле среди всех
других прямых. Решение основано на минимизации:
где g – некоторая функция.
была наилучшей в определенном смысле среди всех
других прямых. Решение основано на минимизации:
где g – некоторая функция.
Слайд 25Метод наименьших квадратов
Наиболее распространена методом наименьших квадратов
(МНК), реализующий минимизацию суммы
квадратов
отклонений:
Основные особенности МНК:
Он наиболее простой с вычислительной точки зрения.
Оценки коэффициентов регрессии по МНК при определенных предпосылках обладают рядом оптимальных свойств.
отклонений:
Основные особенности МНК:
Он наиболее простой с вычислительной точки зрения.
Оценки коэффициентов регрессии по МНК при определенных предпосылках обладают рядом оптимальных свойств.
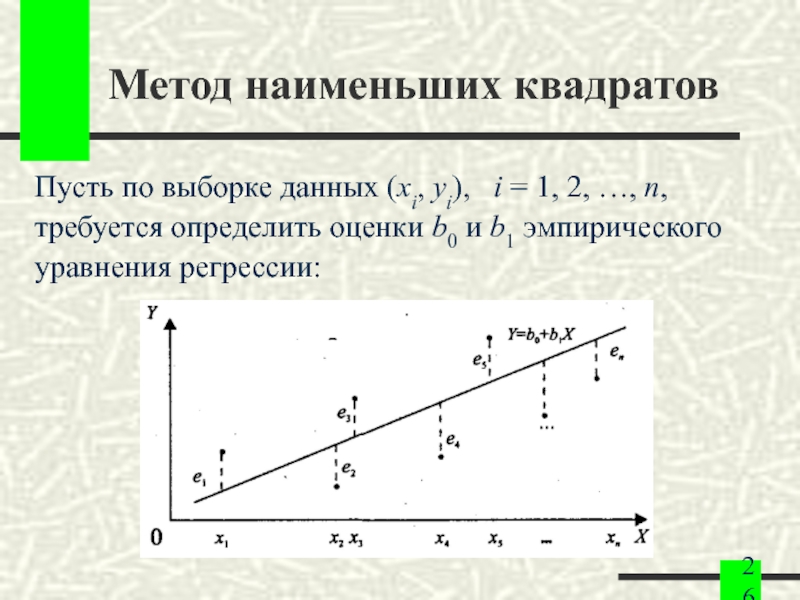
Слайд 26Метод наименьших квадратов
Пусть по выборке данных (xi, yi), i =
1, 2, …, n,
требуется определить оценки b0 и b1 эмпирического
уравнения регрессии:
требуется определить оценки b0 и b1 эмпирического
уравнения регрессии:
Слайд 27Метод наименьших квадратов
В этом случае минимизируется функция:
Т.к. функция Q(b0,b1) непрерывна, выпукла
и ограничена
снизу, то она имеет минимум.
снизу, то она имеет минимум.
Необходимым условием минимума Q(b0,b1) является
равенство нулю ее частных производных по неизвестным
параметрам b0 и b1.
Слайд 28Метод наименьших квадратов
Приравняем нулю частные производные и затем
разделим на n оба
уравнения:
Слайд 31Выводы
1. Оценки МНК являются функциями от выборки, что позволяет
их легко рассчитать.
2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.
3. Эмпирическая прямая регрессии обязательно проходит через точку
2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.
3. Эмпирическая прямая регрессии обязательно проходит через точку
Слайд 32Выводы
4. Эмпирическое уравнение регрессии построено так, что
5. Случайные отклонения
ei не коррелированы с наблюдаемыми значениями yi зависимой переменной Y.
6. Случайные отклонения ei не коррелированы с наблюдаемыми значениями xi независимой переменной X.
6. Случайные отклонения ei не коррелированы с наблюдаемыми значениями xi независимой переменной X.
Слайд 33Другие методы определения коэффициентов регрессии
Другие методы определения коэффициентов регрессии:
метод наименьших модулей
(МНМ),
метод моментов (ММ),
метод максимального правдоподобия (ММП).
метод моментов (ММ),
метод максимального правдоподобия (ММП).
Слайд 34Пример (A) построения уравнения регрессии
При анализе зависимости объема потребления Y (у.е.)
домохозяйства
от располагаемого дохода X (у.е.) отобрана
выборка объема n = 12 (помесячно в течение года),
результаты которой приведены в таблице:
выборка объема n = 12 (помесячно в течение года),
результаты которой приведены в таблице:
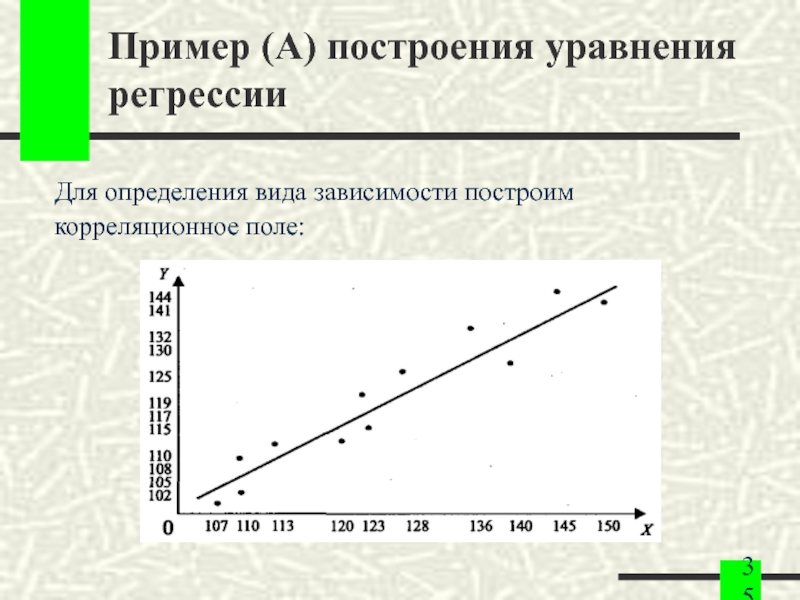
Слайд 35Пример (A) построения уравнения регрессии
Для определения вида зависимости построим
корреляционное поле:
Слайд 36Пример (A) построения уравнения регрессии
По расположению точек на корреляционном поле
делаем предположение
о линейной зависимости:
Согласно МНК, имеем:
Согласно МНК, имеем:
Слайд 37Пример (A) построения уравнения регрессии
Т.о., уравнение парной линейной регрессии имеет вид:
Изобразим
данную прямую регрессии на корреляционном
поле. По этому уравнению рассчитаем , а также
Для анализа степени линейной зависимости вычислим:
Отсюда можно сделать вывод о сильной прямой линейной
зависимости между переменными.
поле. По этому уравнению рассчитаем , а также
Для анализа степени линейной зависимости вычислим:
Отсюда можно сделать вывод о сильной прямой линейной
зависимости между переменными.






![Регрессионные моделиMx[Y] = ϕ(X) − парная регрессия,Mx[Y] = ϕ(X1,…,Xm) − множественная регрессия,где ϕ(X) ≠ const,](/img/tmb/4/353496/d54d26c7b736a426e5101d459903f2df-800x.jpg)


![Регрессионные уравненияY = M[Y/x] + ε = ϕ(x) + ε − уравнение парной регрессии,Y =](/img/tmb/4/353496/408db98e3a0ba748dd396962af9cff5d-800x.jpg)