пространстве.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямых в пространстве презентация
Содержание
- 1. Параллельность прямых в пространстве
- 2. Аксиомы группы С1 Какова бы
- 3. Аксиомы группы
- 4. Аксиомы группы С3 Если две
- 5. Через
- 6. Если две точки прямой принадлежат плоскости, то
- 7. Через 3 точки, не лежащие на одной
- 8. Через две ПАРАЛЛЕЛЬНЫЕ прямые проходит плоскость, и притом только одна. к Следствие из Т1
- 9. Вывод Как в
- 10. Дано: АВСD-параллелограмм А, В, С ∈
- 12. скрещиваются скрещиваются: 1) не пересекаются 2) не
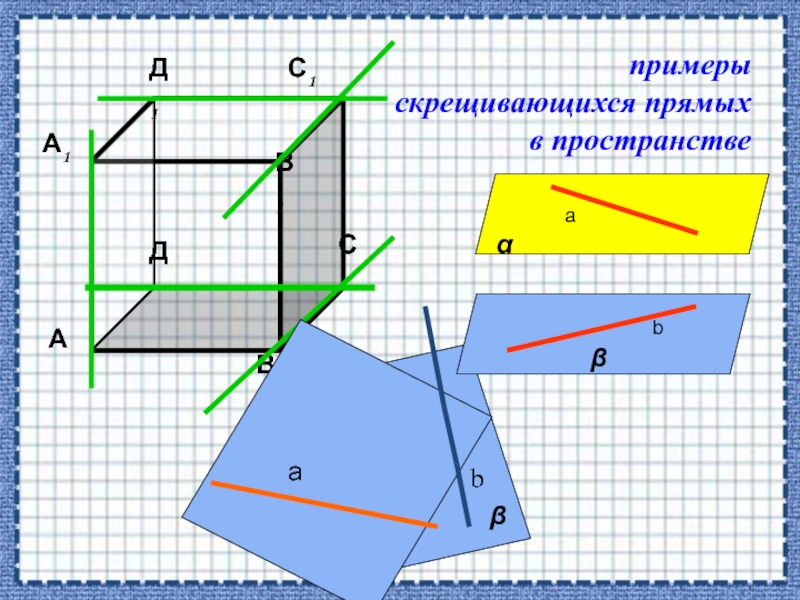
- 13. α примеры скрещивающихся прямых
- 18. Через конец А отрезка АВ проведена плоскость.
Аксиомы группы С1 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. А К D
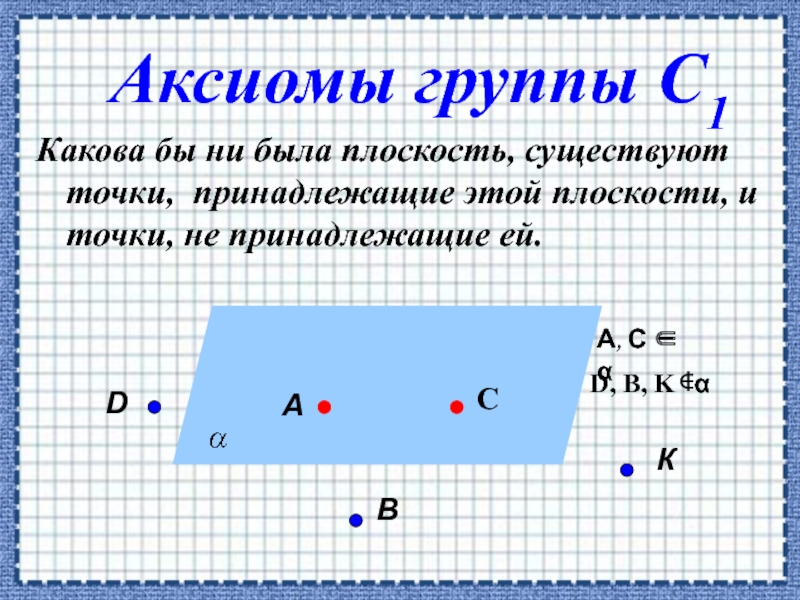
Слайд 2 Аксиомы группы С1
Какова бы ни была плоскость, существуют точки,
принадлежащие этой плоскости, и точки, не принадлежащие ей.
А
К
D
B
С
А, С ∈ α
D, B, K ∉α
Слайд 3
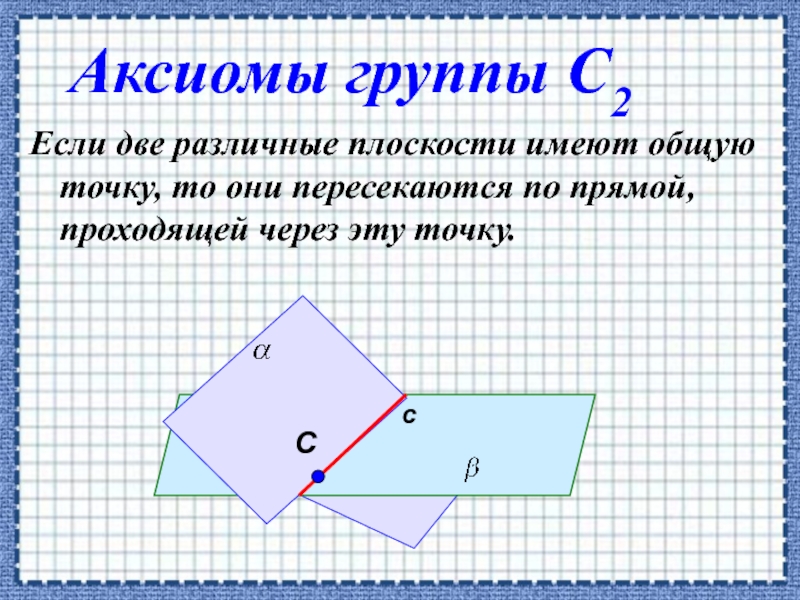
Аксиомы группы С2
Если две различные плоскости имеют
общую точку, то они пересекаются по прямой, проходящей через эту точку.
С
с
Слайд 4 Аксиомы группы С3
Если две различные прямые имеют общую точку,
то через них можно провести плоскость, и притом только одну.
a
b
С
Слайд 5 Через любую прямую и не
принадлежащую ей точку можно провести плоскость, и притом только одну.
α
М
Следствия из аксиом
Т1
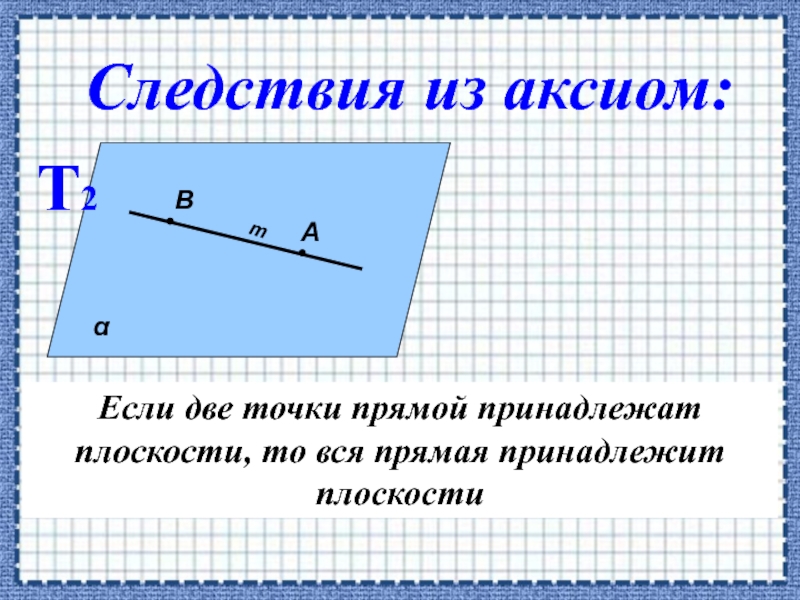
Слайд 6Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости
α
А
В
Следствия из аксиом:
Т2
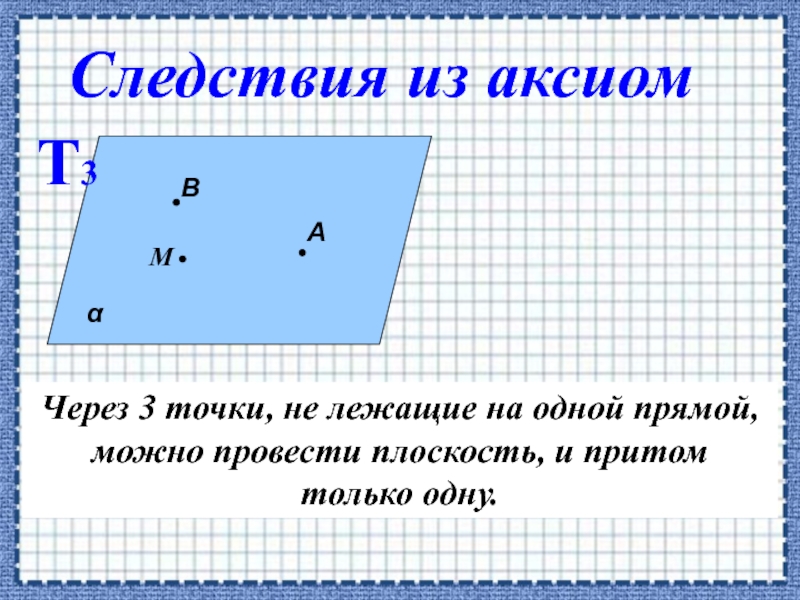
Слайд 7Через 3 точки, не лежащие на одной прямой, можно провести плоскость,
и притом только одну.
α
М
А
В
Следствия из аксиом
Т3
Слайд 9
Вывод
Как в пространстве можно однозначно задать плоскость?
1. По трем точкам
2. По
прямой и не принадлежащей ей точке.
3. По двум пересекающимся прямым.
4. По двум параллельным прямым.
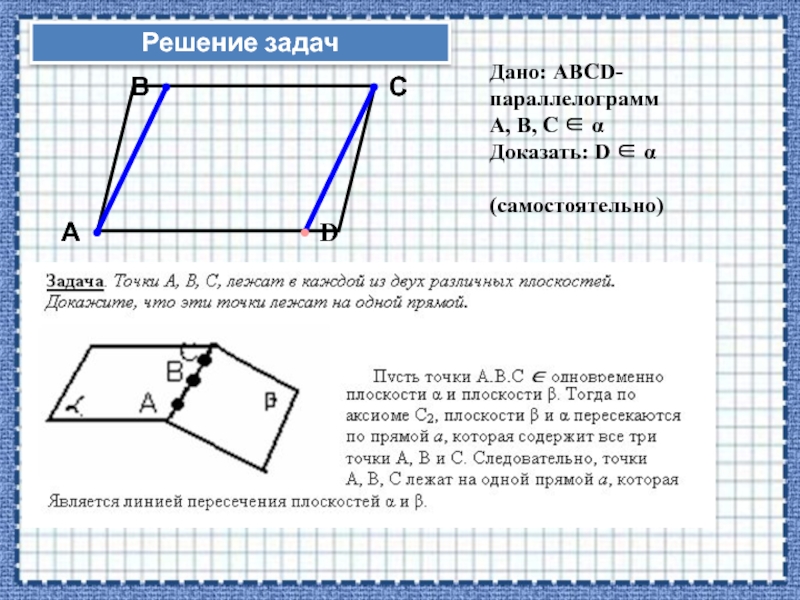
Слайд 10Дано: АВСD-параллелограмм
А, В, С ∈ α
Доказать: D ∈ α
(самостоятельно)
А
В
С
D
•
•
•
•
Доказательство:
А, В ∈ АВ, С,D ∈ СD,
АВ ⎜⎜ СD (по определению параллелограмма) ⇒
АВ, СD ⊂ α ⇒
D ∈ α
Решение задач
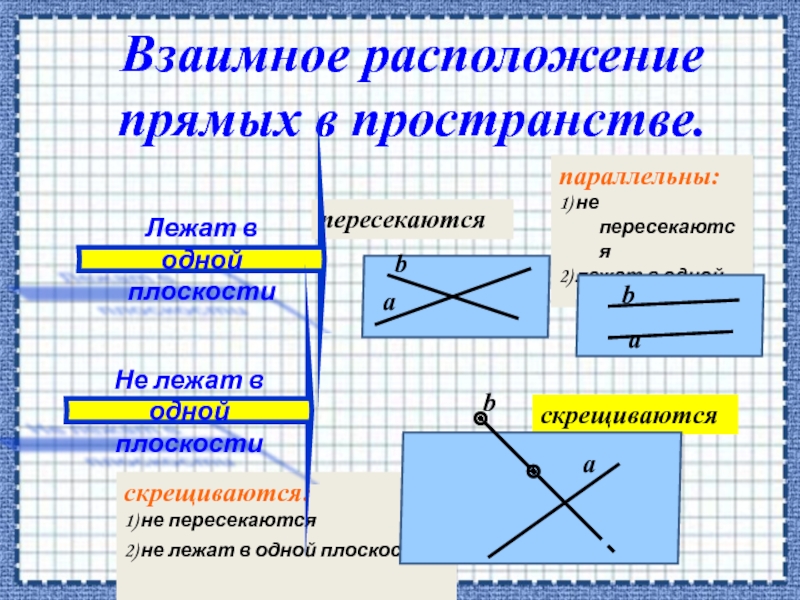
Слайд 12скрещиваются
скрещиваются:
1) не пересекаются
2) не лежат в одной плоскости
параллельны:
1) не пересекаются
2)
лежат в одной плоскости
пересекаются
а
а
а
b
b
b
Взаимное расположение прямых в пространстве.
Лежат в
одной
плоскости
Не лежат в
одной
плоскости
Слайд 18Через конец А отрезка АВ проведена плоскость. Через конец В и
точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если
1) СС1=15 см, АС:ВС=2:3,
2) СС1=8,1 см, АВ:АС=11:9,
3) АВ=6 см, АС:СС1= 2:5,
4) АС=а, ВС=в, СС1=с.
1) СС1=15 см, АС:ВС=2:3,
2) СС1=8,1 см, АВ:АС=11:9,
3) АВ=6 см, АС:СС1= 2:5,
4) АС=а, ВС=в, СС1=с.
Дано: АВ, А∈α, С∈АВ, СС1⎜⎢ВВ1, С1,В1∈α
Найти BB1
