- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность плоскостей в пространстве. Параллельное проецирование. Площадь ортогональной проекции презентация
Содержание
- 1. Параллельность плоскостей в пространстве. Параллельное проецирование. Площадь ортогональной проекции
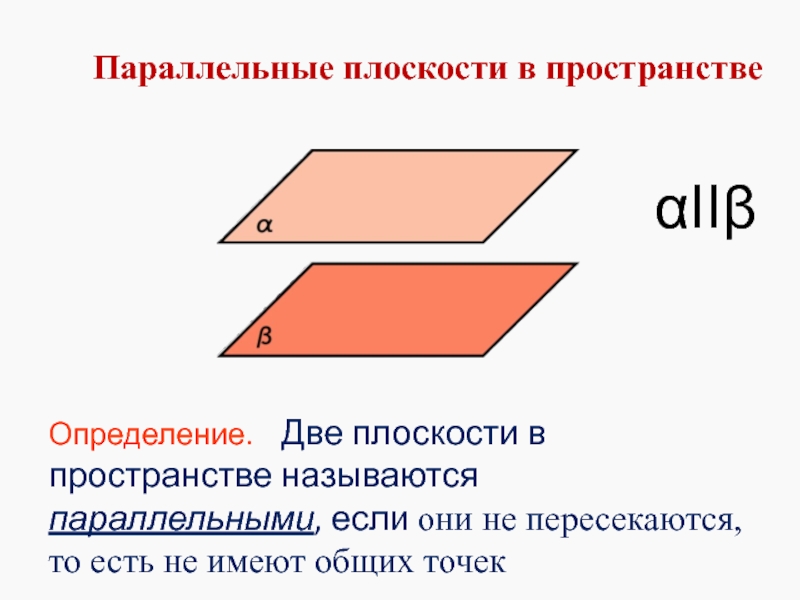
- 2. Параллельные плоскости в пространстве Определение. Две
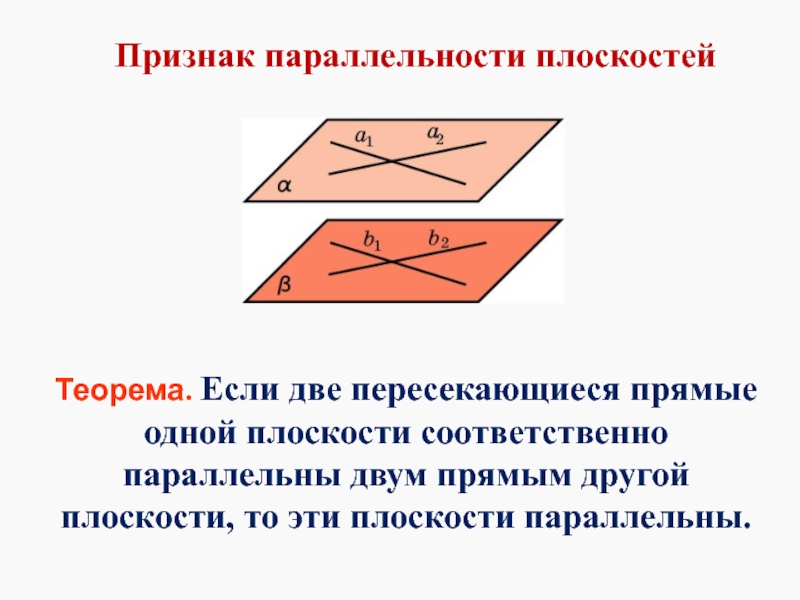
- 3. Признак параллельности плоскостей Теорема. Если две пересекающиеся
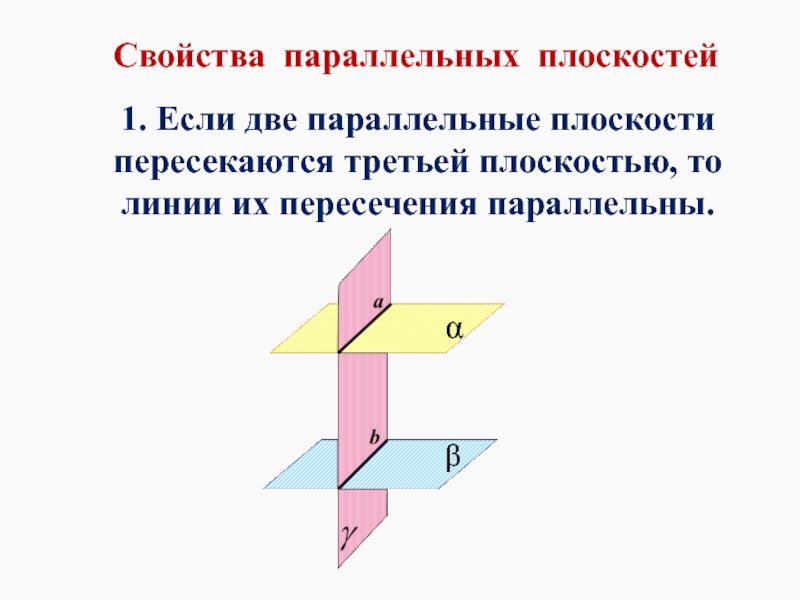
- 4. Свойства параллельных плоскостей 1. Если две параллельные
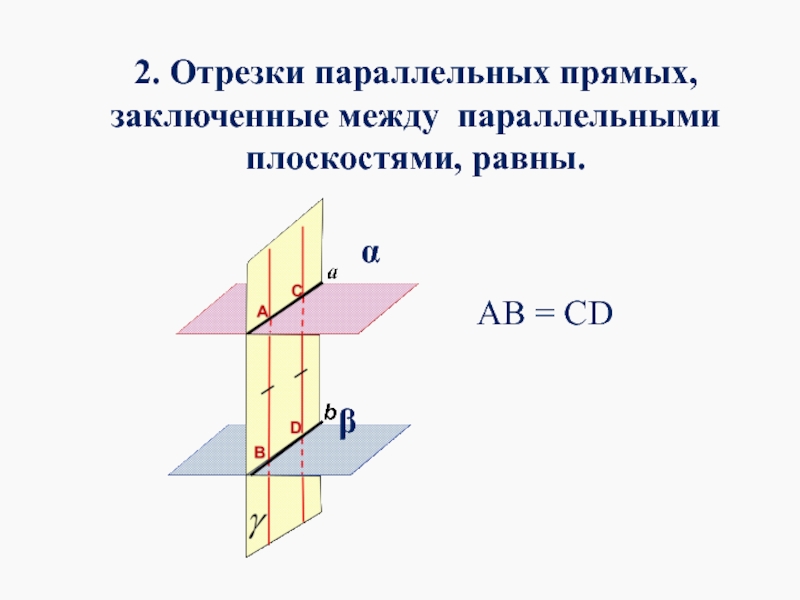
- 5. 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. АВ = СD β α
- 6. Обычно для изображения пространственных фигур на плоскости используется параллельное проектирование пространственной фигуры на плоскость.
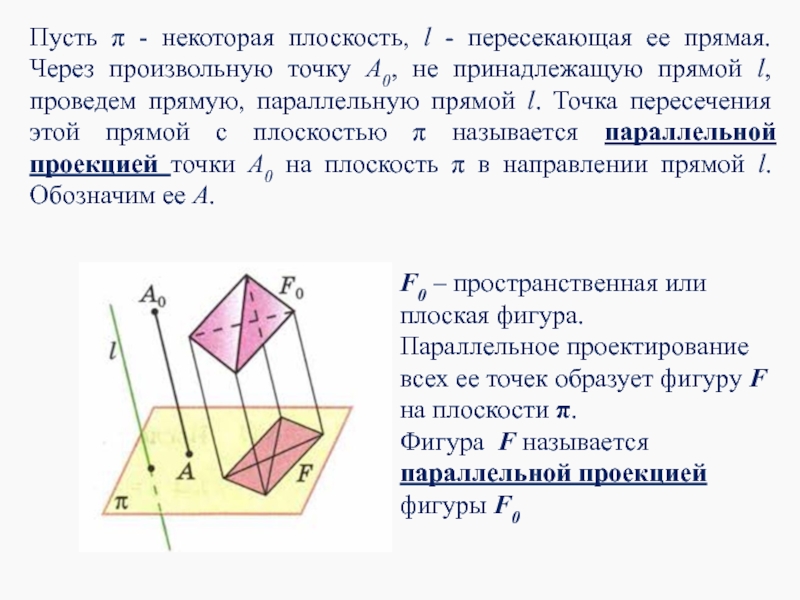
- 7. Пусть π - некоторая плоскость, l -
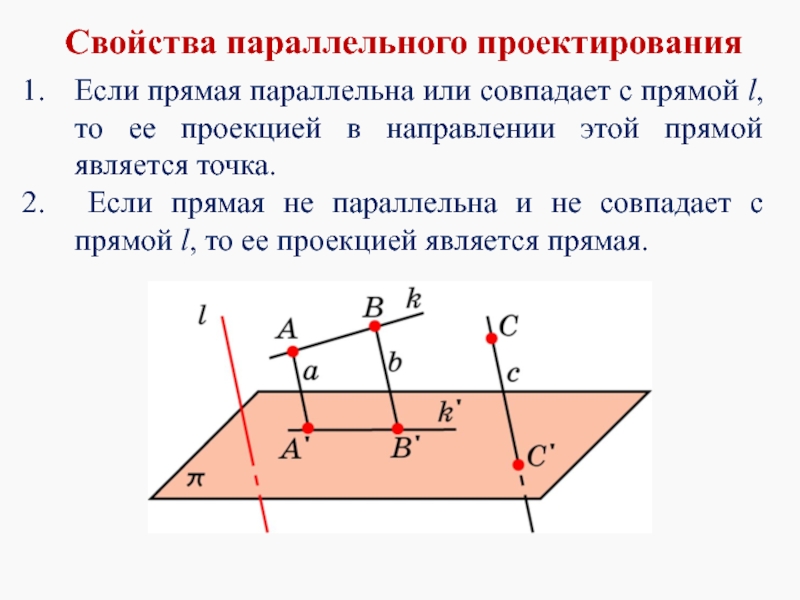
- 8. Свойства параллельного проектирования Если прямая параллельна или
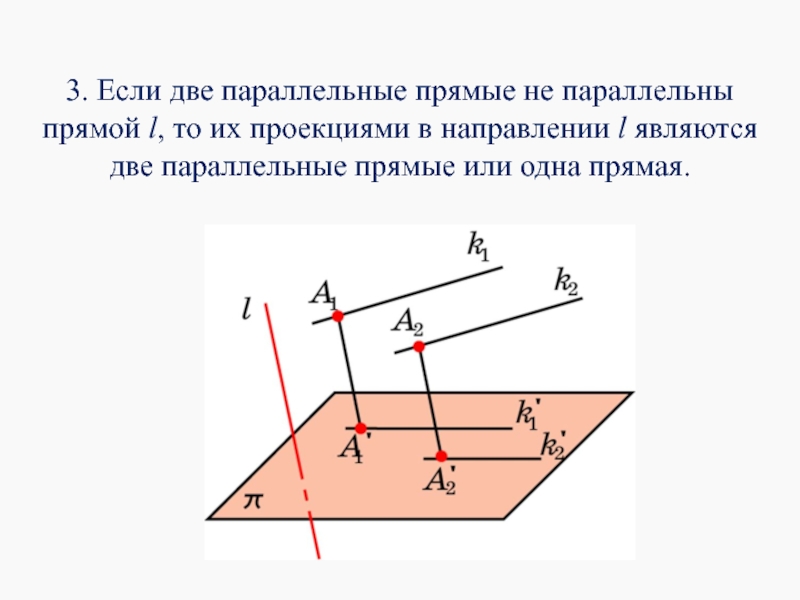
- 9. 3. Если две параллельные прямые не параллельны
- 10. Если прямые параллельны, то они проектируются или
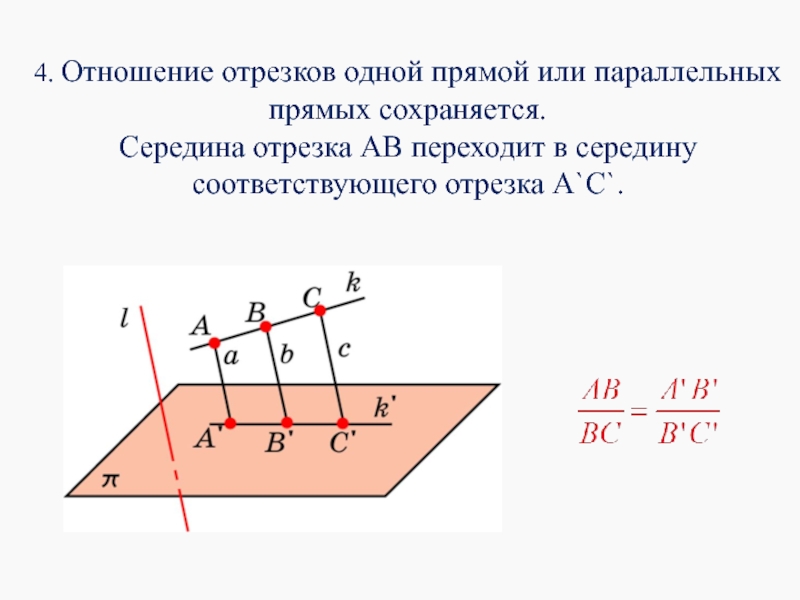
- 11. 4. Отношение отрезков одной прямой или параллельных
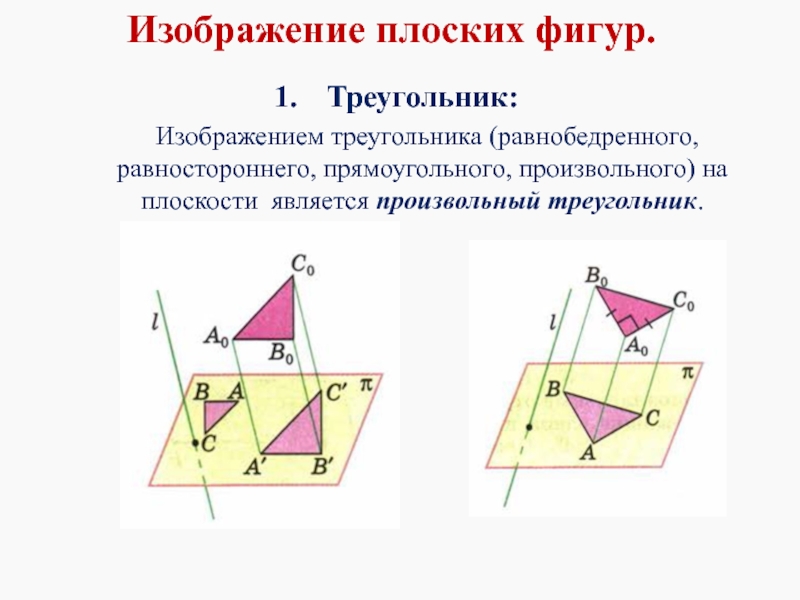
- 12. Изображение плоских фигур. Треугольник:
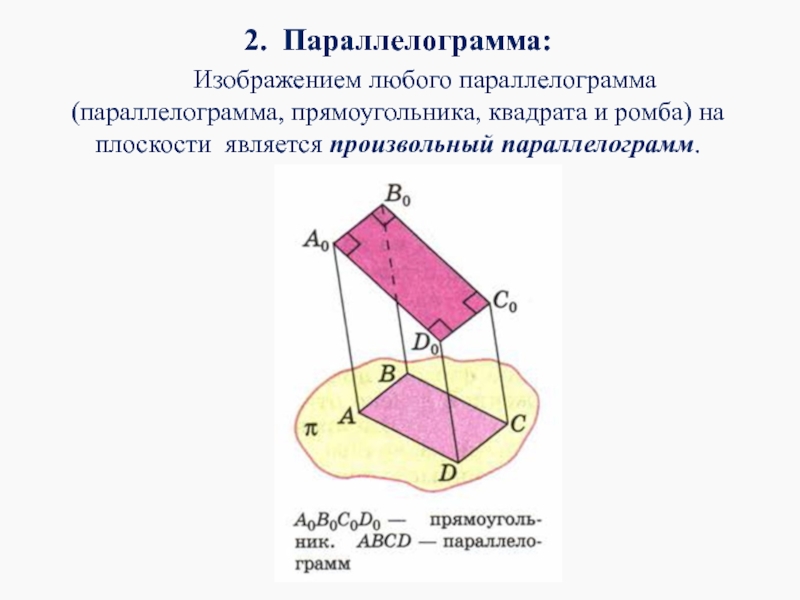
- 13. 2. Параллелограмма: Изображением
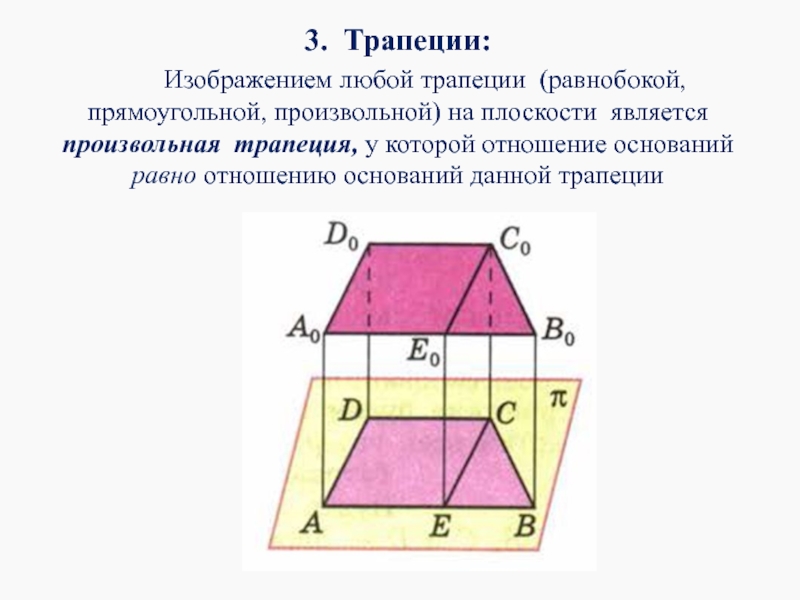
- 14. 3. Трапеции: Изображением
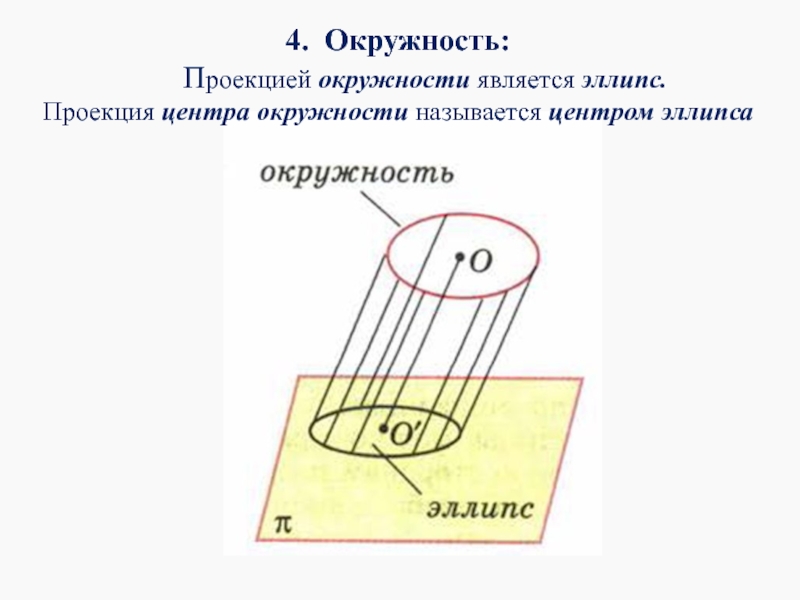
- 15. 4. Окружность: Проекцией
- 16. Ортогональным проектированием называется параллельное проектирование в направлении
- 17. Ортогональной проекцией точки А на данную плоскость
- 18. Теорема. Площадь ортогональной проекции многоугольника на плоскость
- 20. Даны параллельные плоскости α и β. Через
- 21. Точка В не лежит в плоскости треугольника
- 22. Параллельные плоскости α и β пересекают сторону
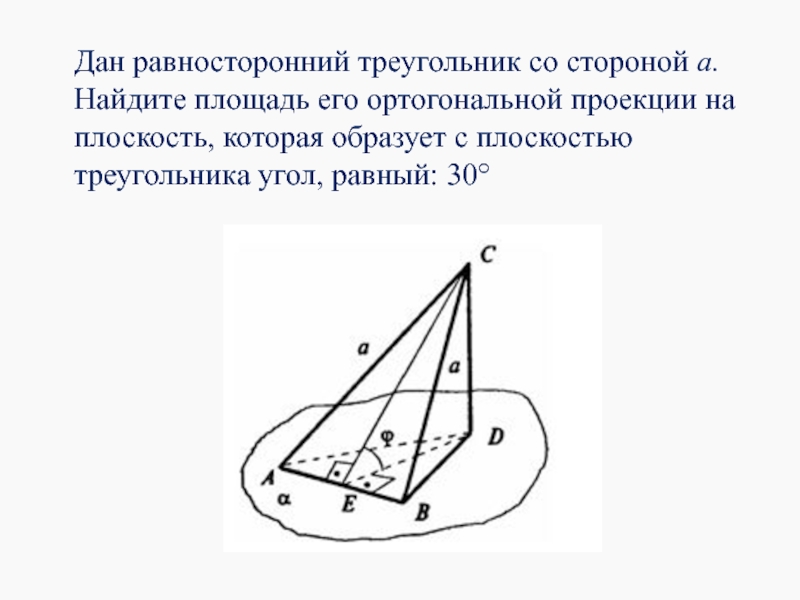
- 23. Дан равносторонний треугольник со стороной а.
Слайд 1Параллельность плоскостей в пространстве.
Параллельное проецирование.
Площадь ортогональной проекции
Слайд 2Параллельные плоскости в пространстве
Определение. Две плоскости в пространстве называются параллельными,
αIIβ
Слайд 3Признак параллельности плоскостей
Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны
Слайд 4Свойства параллельных плоскостей
1. Если две параллельные плоскости пересекаются третьей плоскостью, то
α
β
Слайд 6Обычно для изображения пространственных фигур на плоскости используется параллельное проектирование пространственной
Слайд 7Пусть π - некоторая плоскость, l - пересекающая ее прямая. Через
F0 – пространственная или плоская фигура.
Параллельное проектирование всех ее точек образует фигуру F на плоскости π.
Фигура F называется параллельной проекцией фигуры F0
Слайд 8Свойства параллельного проектирования
Если прямая параллельна или совпадает с прямой l, то
Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Слайд 93. Если две параллельные прямые не параллельны прямой l, то их
Слайд 10Если прямые параллельны, то они проектируются или в две параллельные прямые
Слайд 114. Отношение отрезков одной прямой или параллельных прямых сохраняется.
Середина отрезка АВ
Слайд 12Изображение плоских фигур.
Треугольник:
Изображением треугольника (равнобедренного, равностороннего, прямоугольного,
Слайд 132. Параллелограмма:
Изображением любого параллелограмма (параллелограмма, прямоугольника, квадрата
Слайд 143. Трапеции:
Изображением любой трапеции (равнобокой, прямоугольной, произвольной)
Слайд 154. Окружность:
Проекцией окружности является эллипс.
Проекция центра
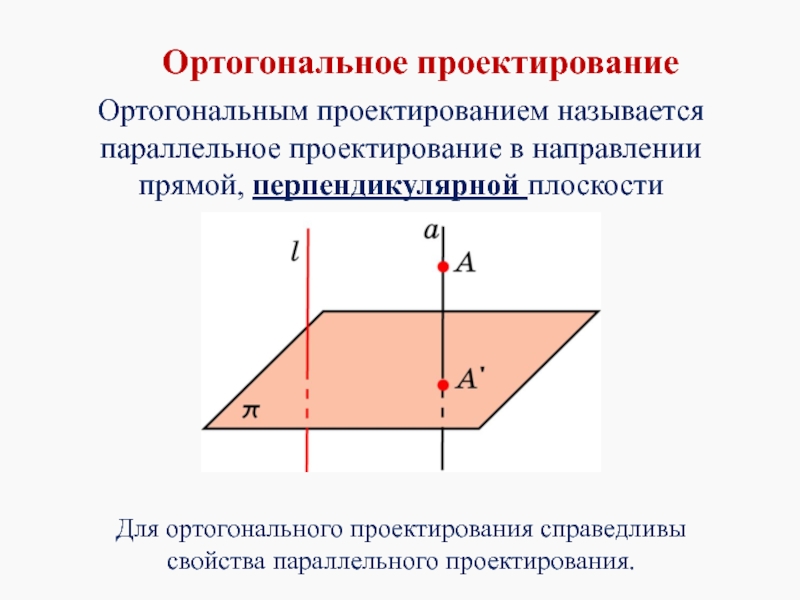
Слайд 16Ортогональным проектированием называется параллельное проектирование в направлении прямой, перпендикулярной плоскости проектирования.
Ортогональное
Для ортогонального проектирования справедливы свойства параллельного проектирования.
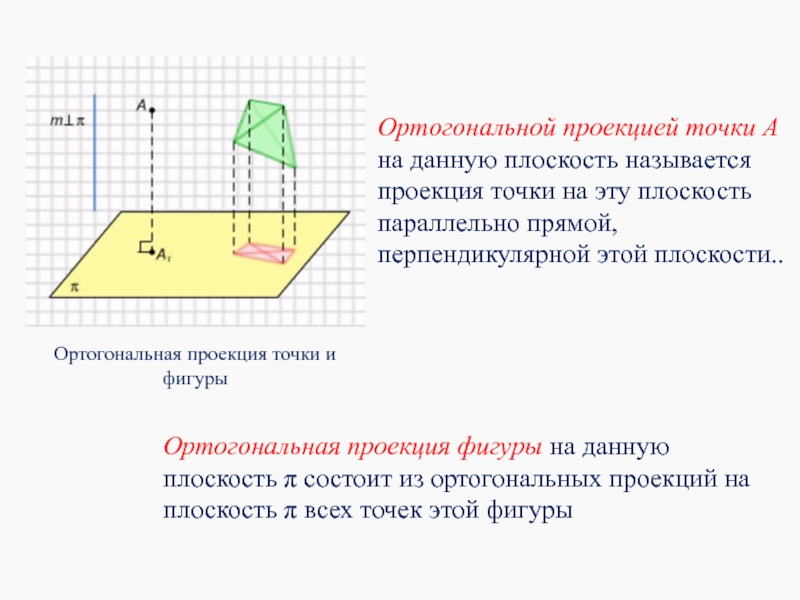
Слайд 17Ортогональной проекцией точки А на данную плоскость называется проекция точки на
Ортогональная проекция точки и фигуры
Ортогональная проекция фигуры на данную плоскость π состоит из ортогональных проекций на плоскость π всех точек этой фигуры
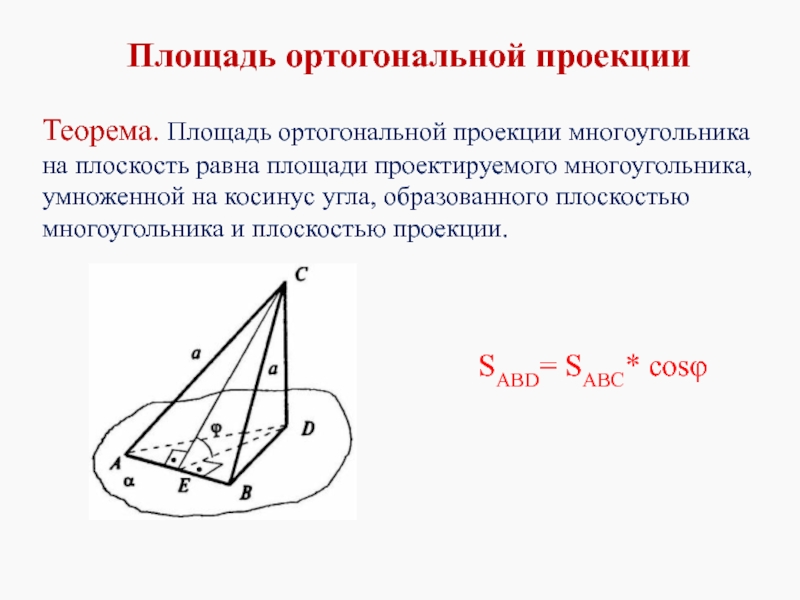
Слайд 18Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника,
SАBD= SABC* cosφ
Площадь ортогональной проекции
Слайд 20Даны параллельные плоскости α и β. Через точки Р и Н
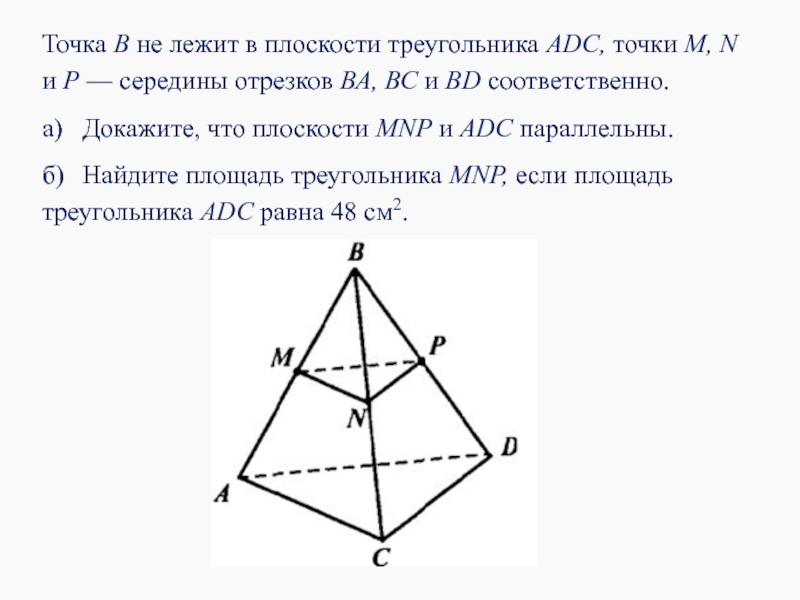
Слайд 21Точка В не лежит в плоскости треугольника ADC, точки М, N
а) Докажите, что плоскости MNP и ADC параллельны.
б) Найдите площадь треугольника MNP, если площадь треугольника ADC равна 48 см2.
Слайд 22Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно
Найдите:
АА2 и АВ2, если А1А2 = 2А1А = 12 см,
АВ, = 5 см;