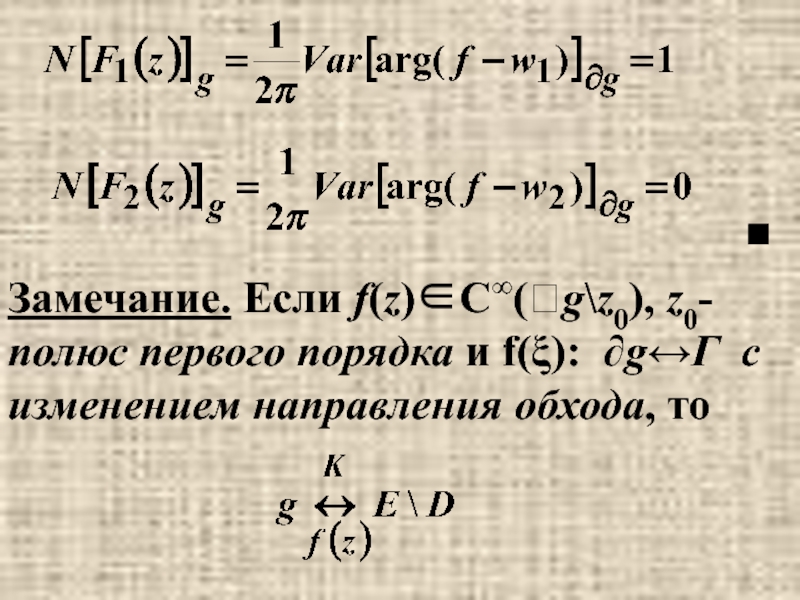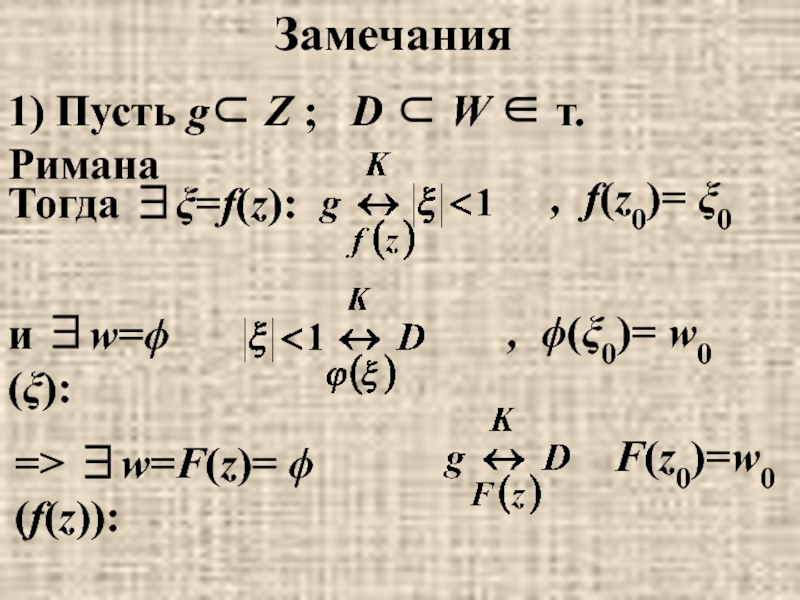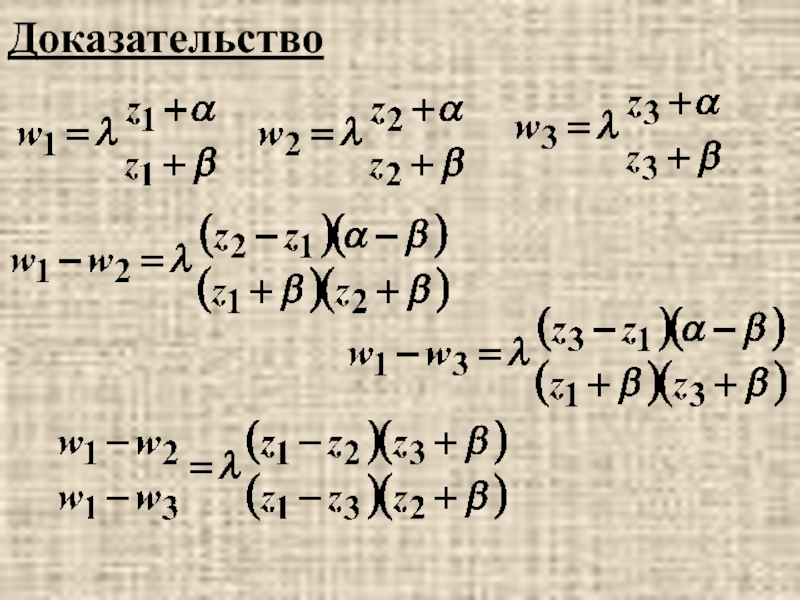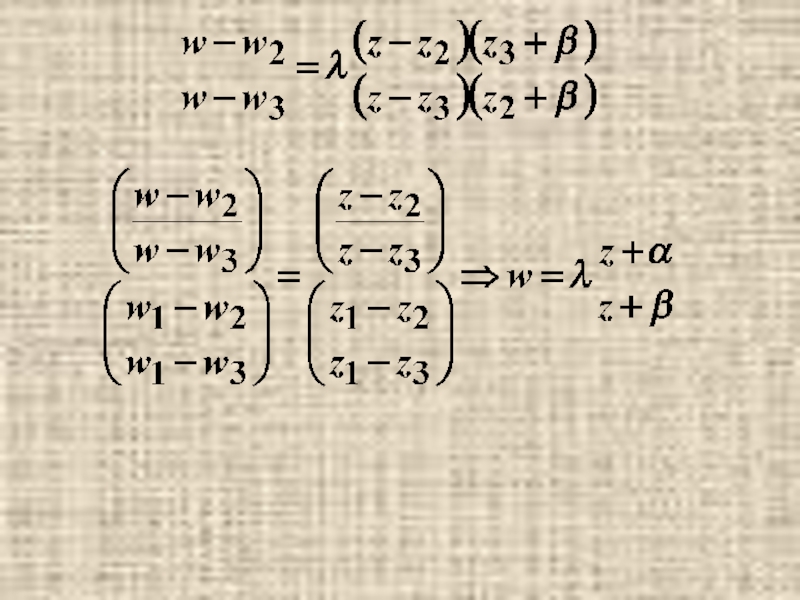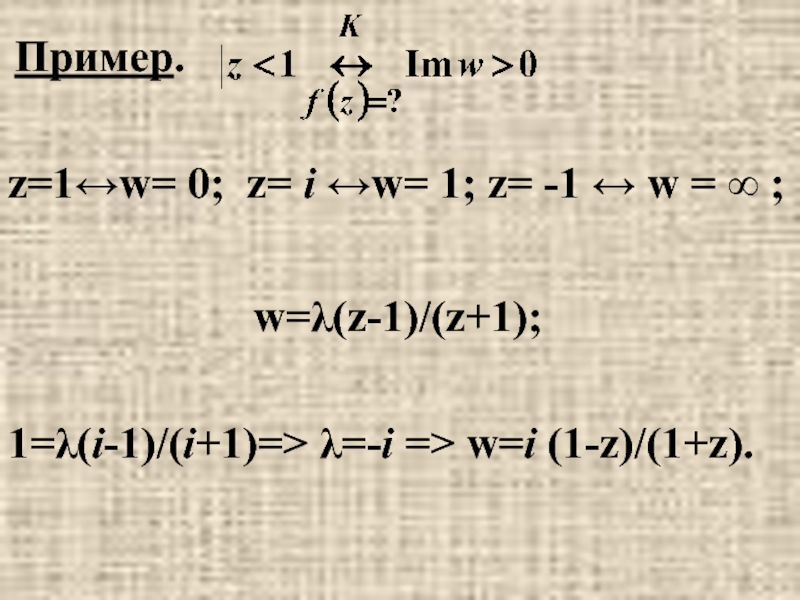- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конформные отображения презентация
Содержание
- 1. Конформные отображения
- 2. Определение обладающее свойствами сохранения углов и постоянства
- 3. Основное определение. Непрерывное взаимно однозначное области
- 4. Теорема 20.1 Если f(z)∈C∞(g), однозначная и однолистная,
- 5. Теорема 20.2(обратная) Если , то f(z)∈C∞(g), однолистна,
- 6. Постоянство растяжений => Сохранение углов => ■
- 7. Теорема 20.3. Необходимым и достаточным условием конформного
- 8. Основные принципы конформных отображений. Принцип соответствия
- 9. Доказательство. Докажем, что f(z) однолистна в g,
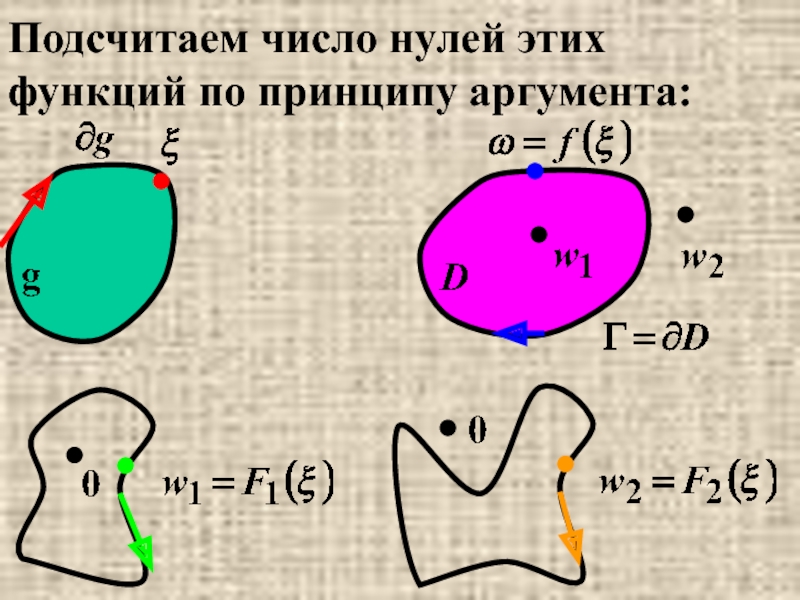
- 10. Подсчитаем число нулей этих функций по принципу
- 11. ■ Замечание. Если f(z)∈C∞(g\z0), z0- полюс первого
- 12. Обратная теорема. Если f(z): (D-ограничена), то
- 13. Теорема Римана Основной закон конформных отображений
- 14. Теорема 20.4. Если g- односвязная g⊂ Z
- 15. Замечания 1) Пусть g⊂ Z ;
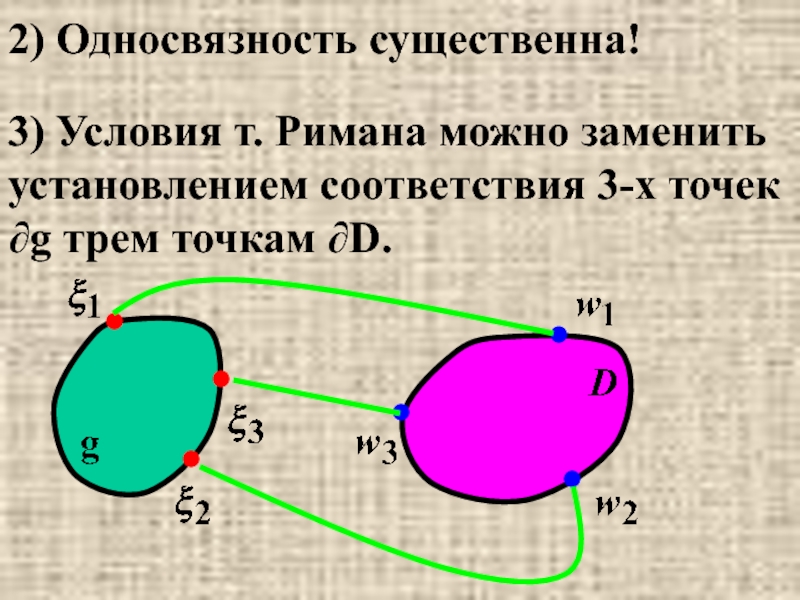
- 17. 2) Односвязность существенна! 3) Условия т. Римана
- 18. п.4. Основные функции, используемые при конформных отображениях.
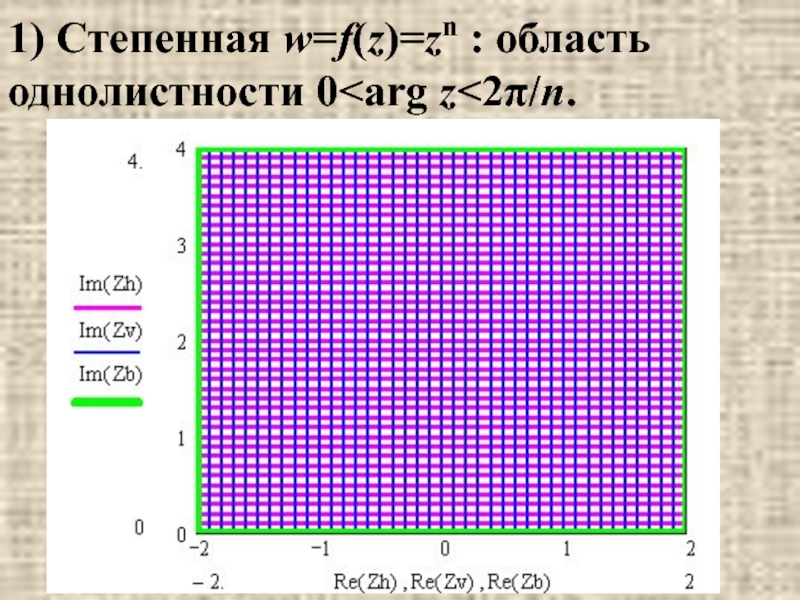
- 19. 1) Степенная w=f(z)=zn : область однолистности 0
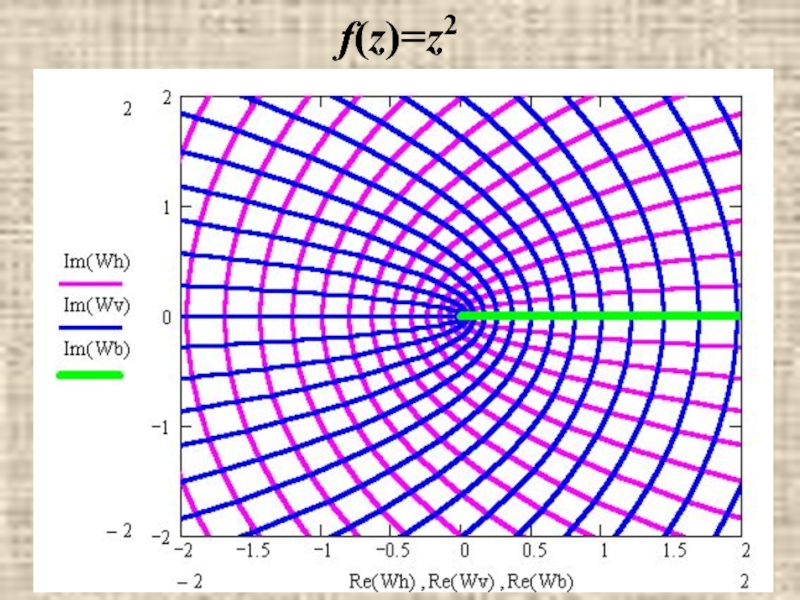
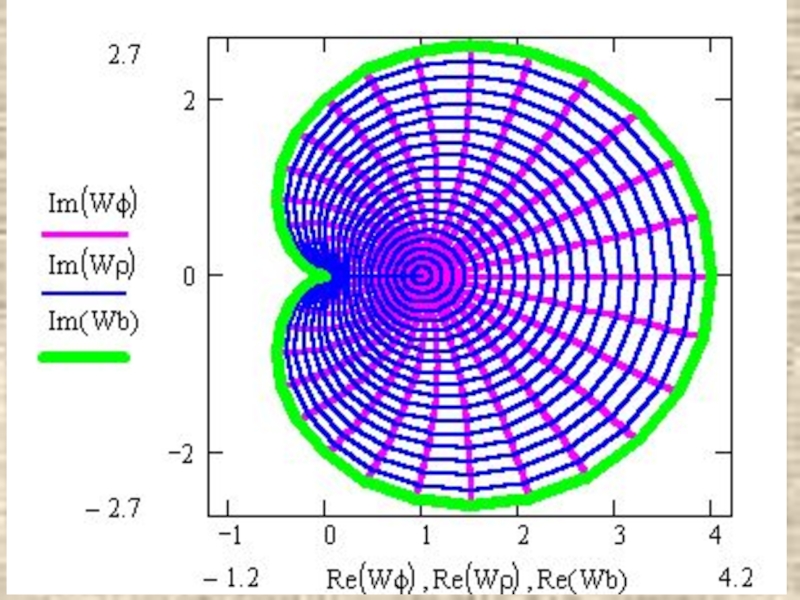
- 20. f(z)=z2
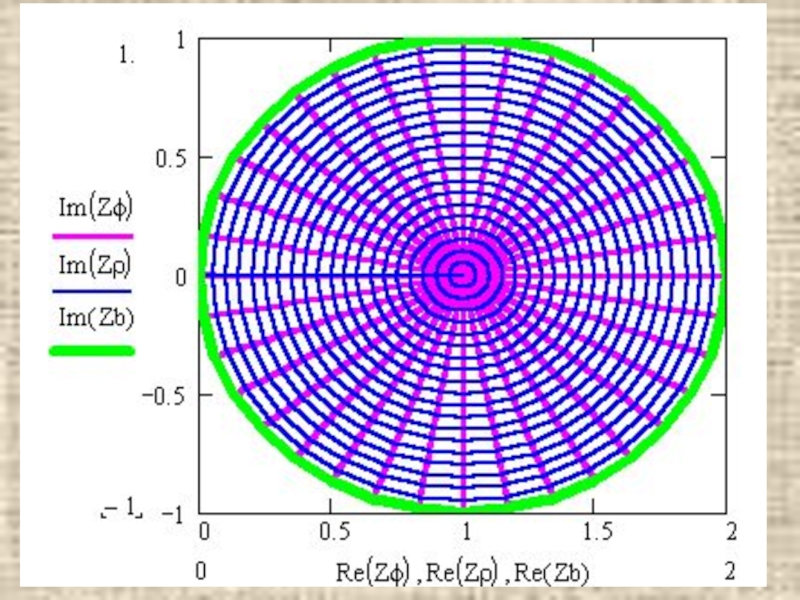
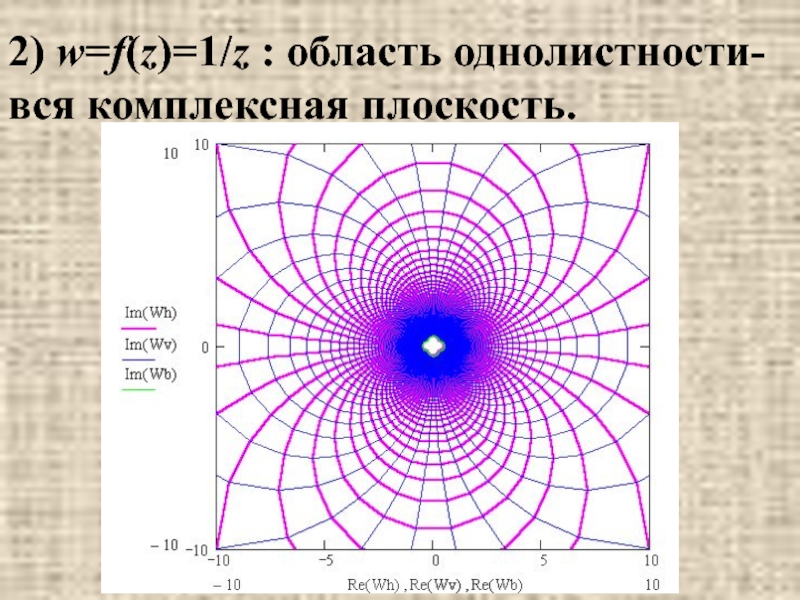
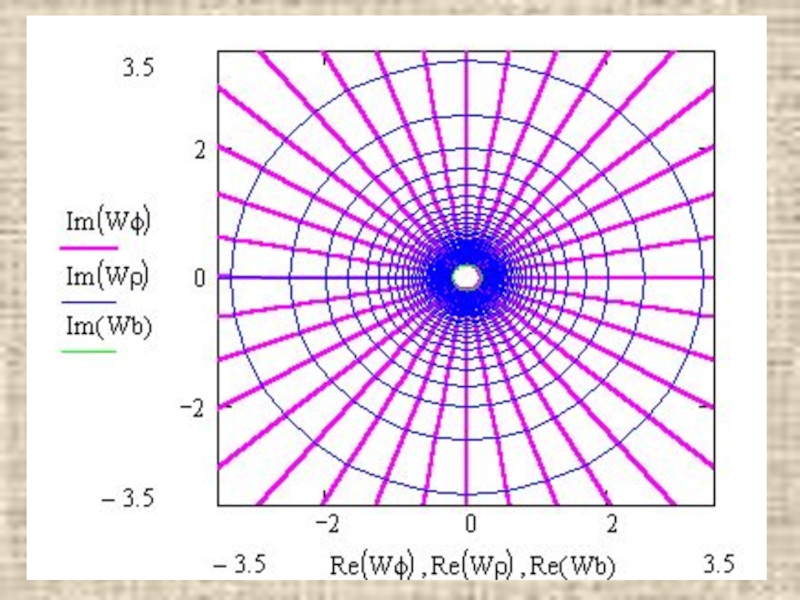
- 23. 2) w=f(z)=1/z : область однолистности- вся комплексная плоскость.
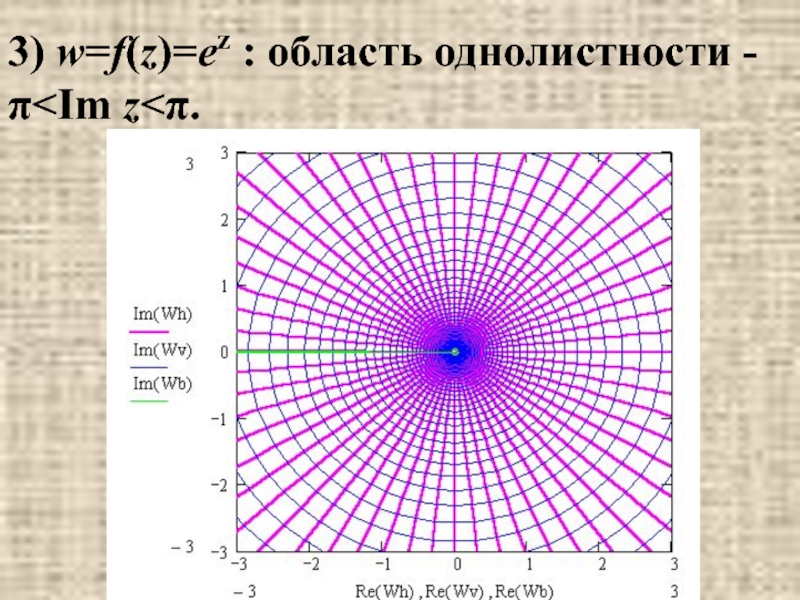
- 25. 3) w=f(z)=ez : область однолистности -π
- 27. Дробно-линейная функция (ДЛФ) 3 параметра, α≠β. , f '(z)≠0 для ∀z
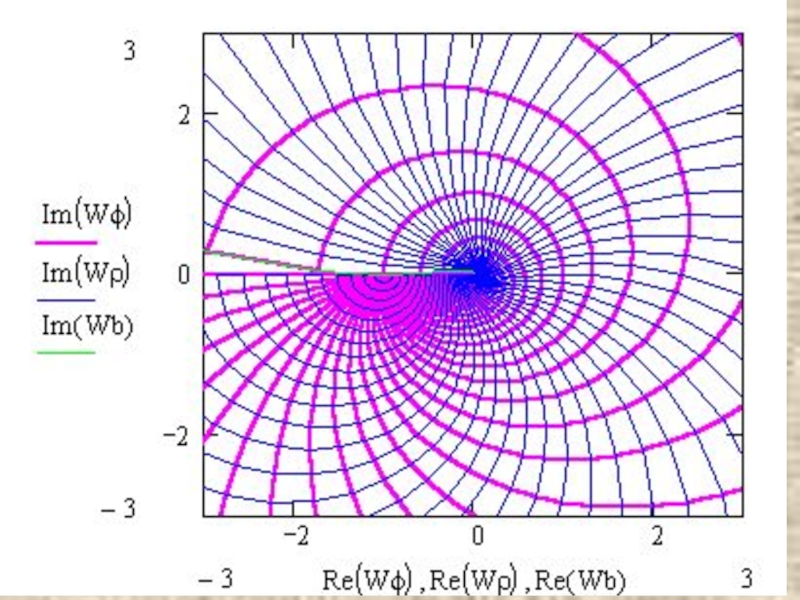
- 28. 1) Геометрический смысл.
- 29. 2) Заданием соответствия z1↔w1, z2↔w2, z3↔w3, ДЛФ
- 30. Доказательство
- 32. Свойства дробно-линейной функции. 1)
- 33. Задав zi↔wi, i=1,2,3 Окружность на плоскости
- 34. Пример. z=1↔w= 0; z= i ↔w= 1;
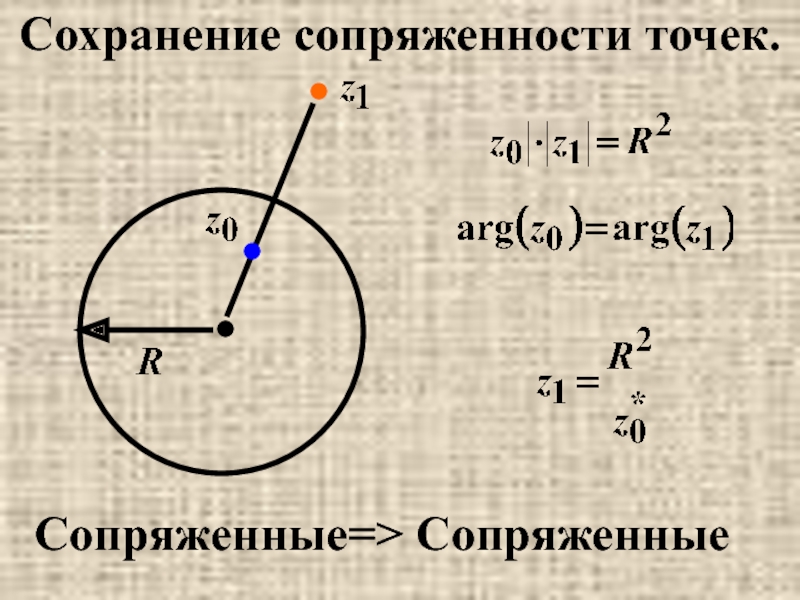
- 35. Сохранение сопряженности точек. Сопряженные=> Сопряженные
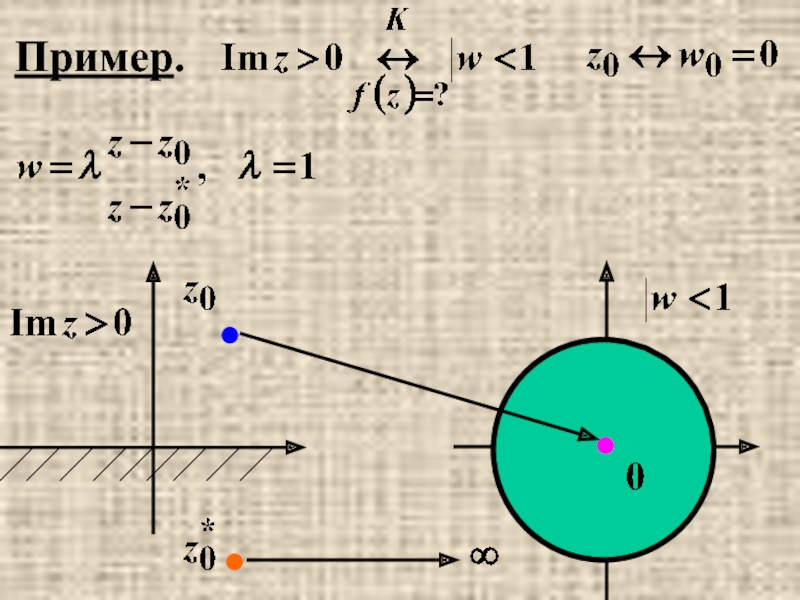
- 36. Пример.
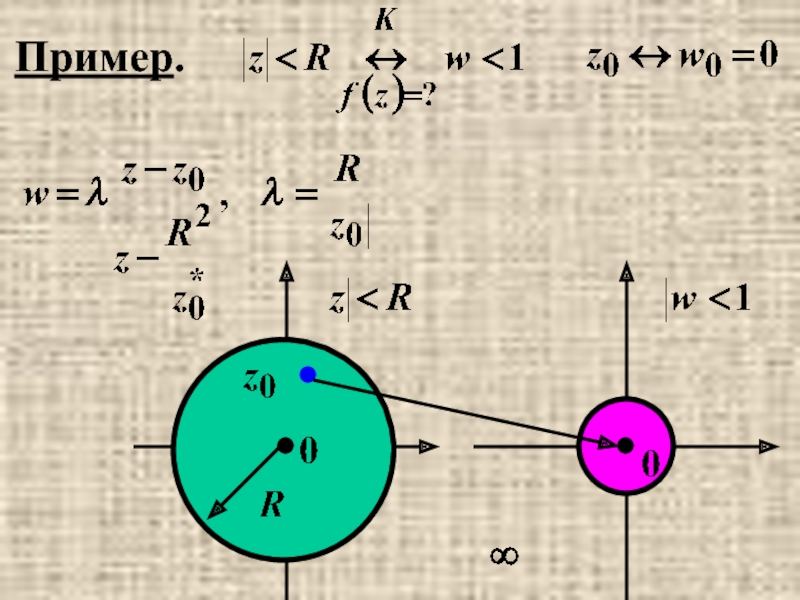
- 37. Пример.
Слайд 2Определение
обладающее свойствами сохранения углов и постоянства растяжений называется конформным отображением в
=> б.м. Ο → б.м. Ο; б.м. Δ → б.м. Δ .
Слайд 3Основное определение.
Непрерывное взаимно однозначное области g⊂ Z ↔ D ⊂
Слайд 4Теорема 20.1 Если f(z)∈C∞(g), однозначная и однолистная, и f ’(z)≠0,
∀z∈g,
Доказательство. Данное отображение f(z) обладает свойствами сохранения углов и постоянства растяжений
(см. выше). ■
Слайд 5Теорема 20.2(обратная) Если
, то f(z)∈C∞(g), однолистна, и f ’(z)≠0, ∀z∈g.
Доказательство.
, то f(z)- непрерывна, однозначна и однолистна.
Слайд 6Постоянство растяжений =>
Сохранение углов =>
■
Замечание. Свойство f ’(z)≠0, ∀z∈g является следствием
Слайд 7Теорема 20.3. Необходимым и достаточным условием конформного отображения является f(z)∈C∞(g), однозначна
Доказательство. Необходимость доказана выше (Теорема 20.2).
Достаточность. См. "А.Г.Свешников, А.Н.Тихонов Теория функций комплексной переменной." М.: Наука-Физматлит 1999, с.156.
Слайд 8Основные принципы конформных отображений.
Принцип соответствия границ. Если f(z)∈C
∂g⬄Γ=∂D плоскости w с сохранением направления обхода, то
Слайд 9Доказательство. Докажем, что f(z) однолистна в g, т.е.
а) ∀w1∈D ∃!
б) ∀w2∉D не ∃ ни одной z2∈g: f(z2)=w2. Рассмотрим две произвольные точки w1∈D и w2∉D и построим в g вспомогательные функции
F1(z)=f(z)-w1, F2(z)=f(z)-w2 , z∈g.
Слайд 11■
Замечание. Если f(z)∈C∞(g\z0), z0- полюс первого порядка и f(ξ): ∂g↔Γ с
Слайд 12Обратная теорема. Если f(z):
(D-ограничена), то f(z)∈C (∂ g ) и
∂g⬄ ∂D.
Слайд 13Теорема Римана
Основной закон конформных отображений
g⊂ Z ; D
Теорема Римана. Если g- односвязная g⊂ Z , ∂ g состоит более чем из одной
точки, то
Слайд 14Теорема 20.4. Если g- односвязная g⊂ Z , ∂ g состоит
так что f(z0) = 0 и arg f '(z0)=α, z0∈g и α- заданные числа.
точки, то ∃! f(z)∈C∞(g):
Полное доказательство см. А.В.Бицадзе "Основы теории аналитических функций".
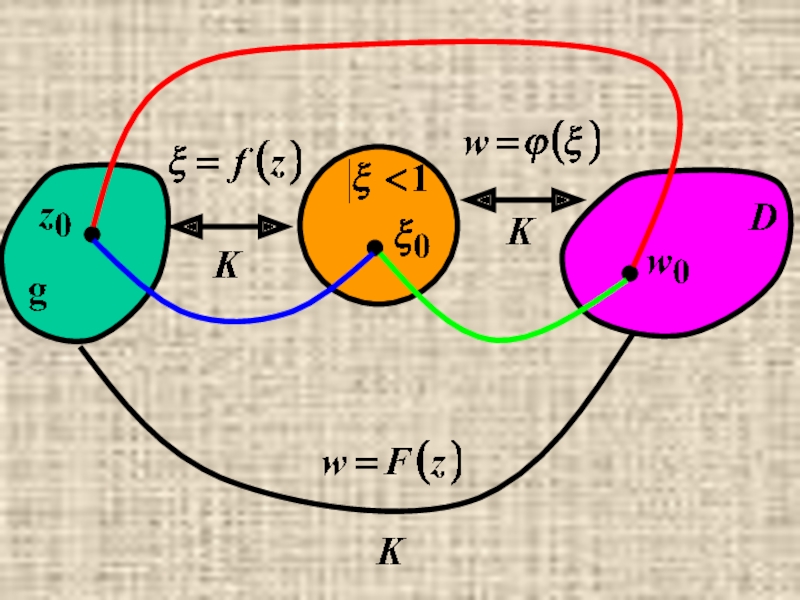
Слайд 15Замечания
1) Пусть g⊂ Z ; D ⊂ W ∈
Тогда ∃ξ=f(z):
, f(z0)= ξ0
и ∃w=ϕ(ξ):
, ϕ(ξ0)= w0
=> ∃w=F(z)= ϕ(f(z)):
F(z0)=w0
Слайд 172) Односвязность существенна!
3) Условия т. Римана можно заменить установлением соответствия 3-х
Слайд 292) Заданием соответствия z1↔w1, z2↔w2, z3↔w3, ДЛФ определена однозначно, т.е. коэффициенты
Слайд 32
Свойства дробно-линейной функции.
1) Круговое:
A(x2+y2)+Bx+Cy+D=0;
z=x+iy=1/ζ=1/(ξ+iη)=
=ξ/(ξ2+η2)-iη/(ξ2+η2)=>
x=ξ/(ξ2+η2), y= -η/(ξ2+η2)
=> A+Bξ-Cη+D(ξ2+η2)=0.
Слайд 33
Задав zi↔wi, i=1,2,3
Окружность на плоскости однозначно определяется заданием 3-х точек.=>
c сохранением
Слайд 34Пример.
z=1↔w= 0; z= i ↔w= 1; z= -1 ↔ w =
w=λ(z-1)/(z+1);
1=λ(i-1)/(i+1)=> λ=-i => w=i (1-z)/(1+z).