Альбертович, г.Минск
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Паралельне проектування і його властивості. Зображення фігур у стереометрії презентация
Содержание
- 1. Паралельне проектування і його властивості. Зображення фігур у стереометрії
- 2. Ми почали вивчати стереометрію – геометрію у
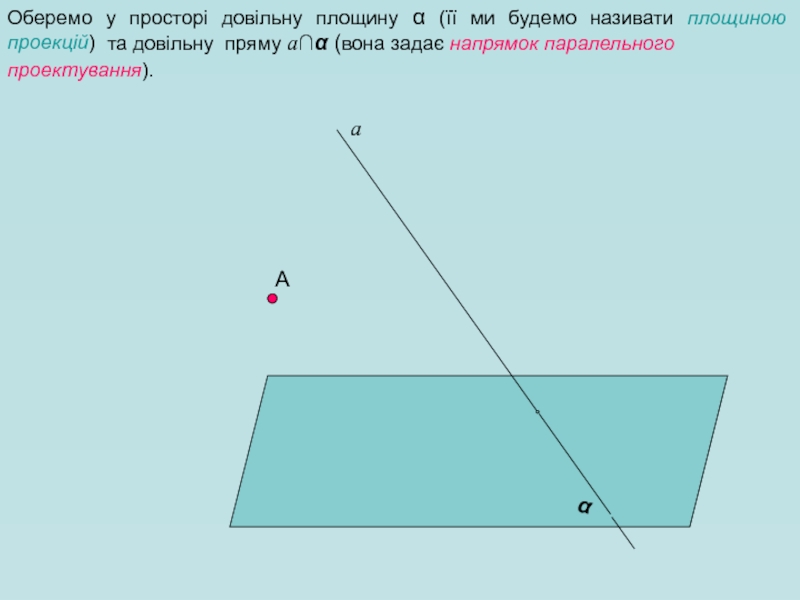
- 3. А Оберемо у просторі довільну площину
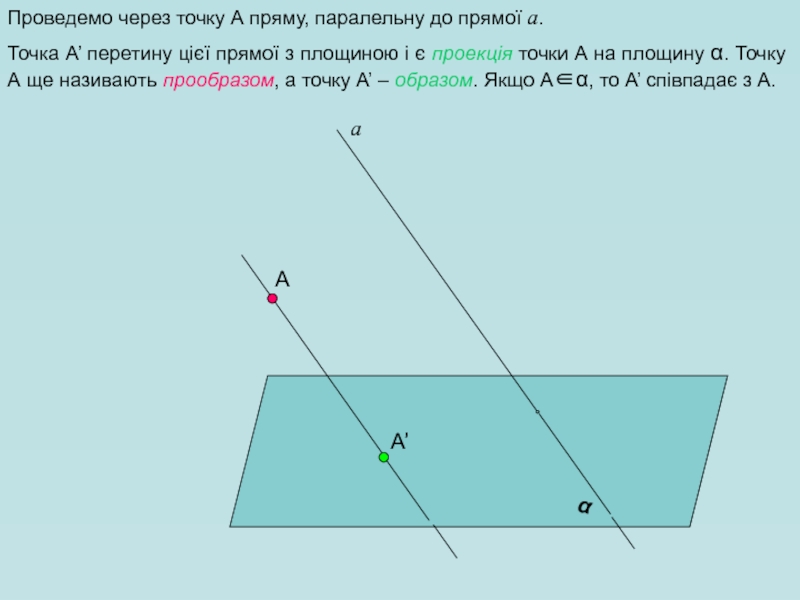
- 4. А α а Проведемо через точку
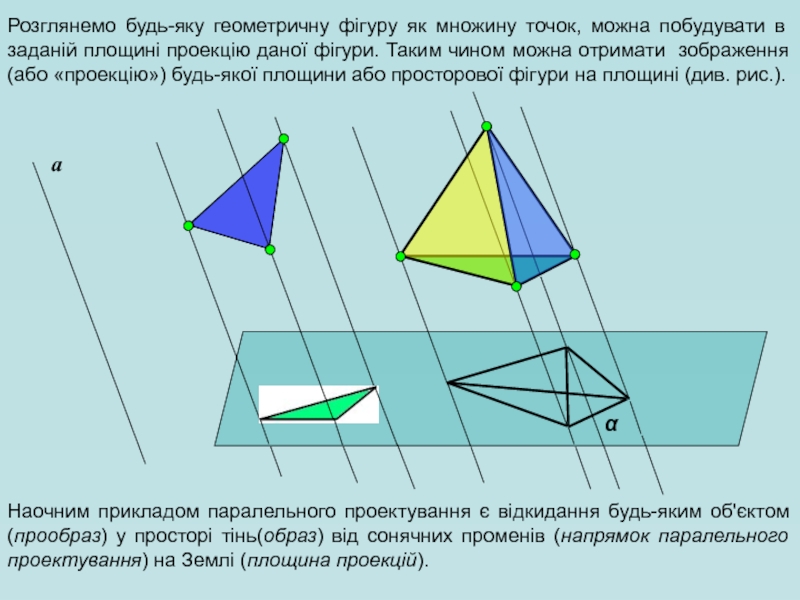
- 5. Розглянемо будь-яку геометричну фігуру
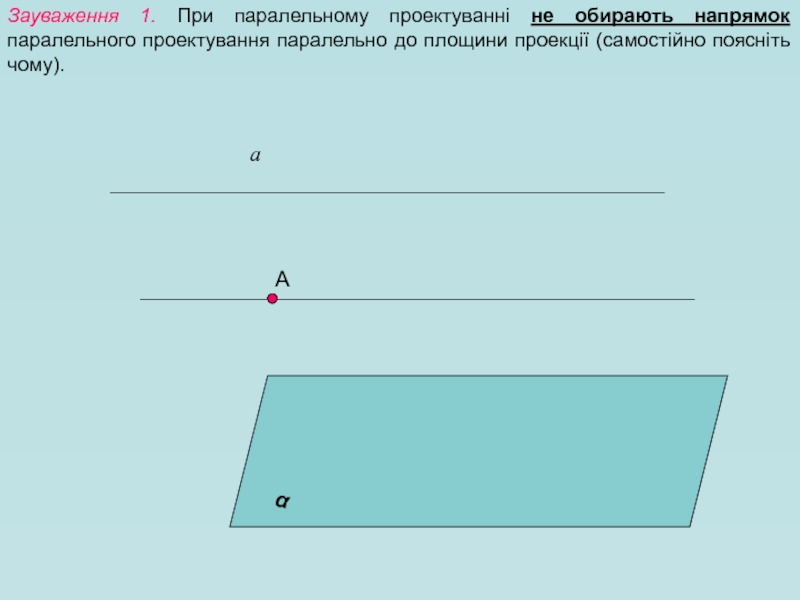
- 6. Зауваження 1. При паралельному проектуванні не обирають
- 7. Зауваження 2. При паралельному проектуванні
- 8. Зауваження 3. Якщо напрямок паралельного
- 9. Зауваження 4. Якщо площина проекцій
- 10. Паралельне проектування володіє властивостями: 1) паралельність прямих
- 11. 2) відношення довжин відрізків, які лежать
- 12. Паралельне проектування володіє властивостями: 1) паралельність
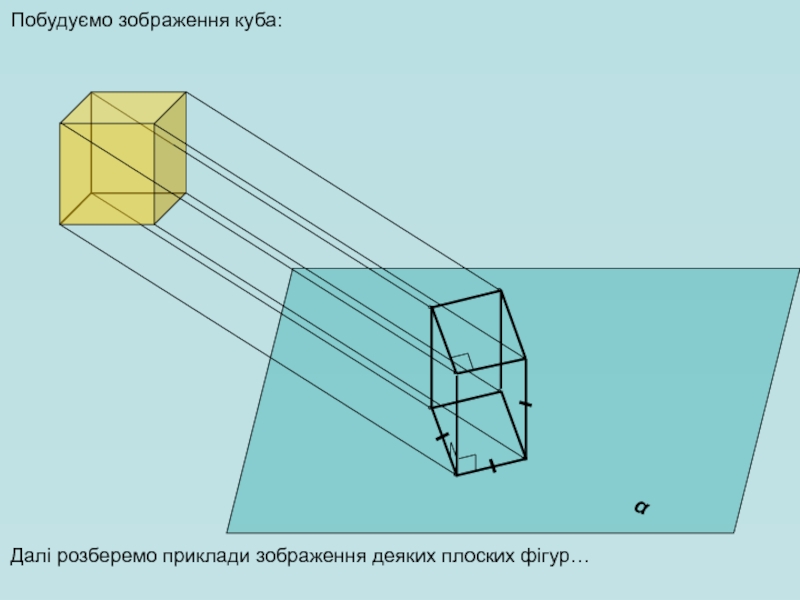
- 13. α Побудуємо зображення куба: Далі розберемо приклади зображення деяких плоских фігур…
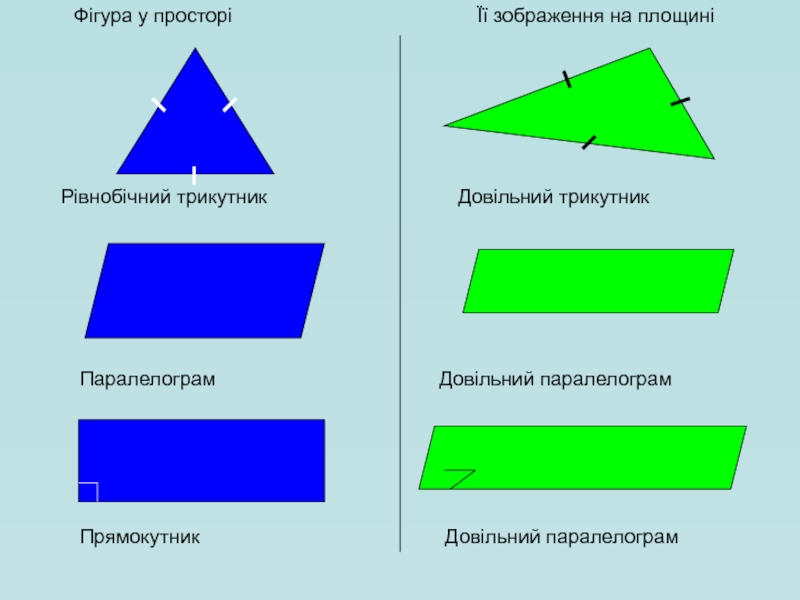
- 14. Фігура у просторі Її зображення на
- 15. Рівнобічний трикутник Довільний трикутник
- 16. Фігура у просторі Її зображення на площині
- 17. Фігура у просторі Її зображення на площині
- 18. A B C D E
- 19. A B C D E
Ми почали вивчати стереометрію – геометрію у просторі. Як завжди нам необхідно вміти зображувати геометричні фігури, причому всі креслення ми і досі виконуємо на площині (на сторінці зошита, на дошці тощо).
Слайд 2Ми почали вивчати стереометрію – геометрію у просторі. Як завжди нам
необхідно вміти зображувати геометричні фігури, причому всі креслення ми і досі виконуємо на площині (на сторінці зошита, на дошці тощо). Яким чином просторову фігуру (наприклад , куб) можна «вкласти» до площини?
Для розв'язання цієї задачі приймається метод паралельного проектування. З'ясуємо його суть на прикладі найпростішої геометричної фігури – точки.
Таким чином, у нас є геометрична фігура у просторі – точка А.
А
Слайд 3
А
Оберемо у просторі довільну площину α (її ми будемо називати площиною
проекцій)
α
та довільну пряму a∩α (вона задає напрямок паралельного
проектування).
а
Слайд 4А
α
а
Проведемо через точку А пряму, паралельну до прямої а.
А’
Точка А’ перетину
цієї прямої з площиною і є проекція точки А на площину α. Точку А ще називають прообразом, а точку А’ – образом. Якщо А∈α, то А’ співпадає з А.
Слайд 5
Розглянемо будь-яку геометричну фігуру як множину точок, можна побудувати в заданій
площині проекцію даної фігури. Таким чином можна отримати зображення (або «проекцію») будь-якої площини або просторової фігури на площині (див. рис.).
а
α
Наочним прикладом паралельного проектування є відкидання будь-яким об'єктом (прообраз) у просторі тінь(образ) від сонячних променів (напрямок паралельного проектування) на Землі (площина проекцій).
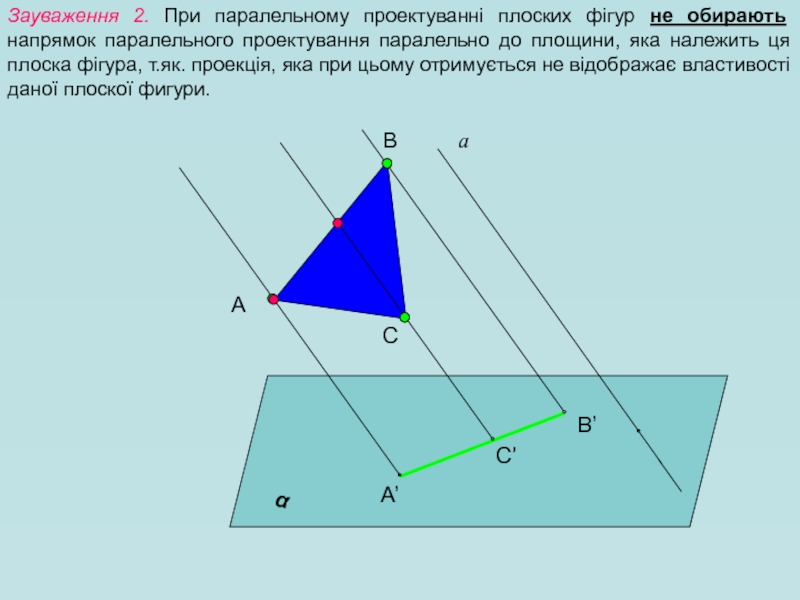
Слайд 6Зауваження 1. При паралельному проектуванні не обирають напрямок паралельного проектування паралельно
до площини проекції (самостійно поясніть чому).
А
а
α
Слайд 7
Зауваження 2. При паралельному проектуванні плоских фігур не обирають напрямок паралельного
проектування паралельно до площини, яка належить ця плоска фігура, т.як. проекція, яка при цьому отримується не відображає властивості даної плоскої фигури.
А
а
α
B
C
А’
B’
C’
Слайд 8
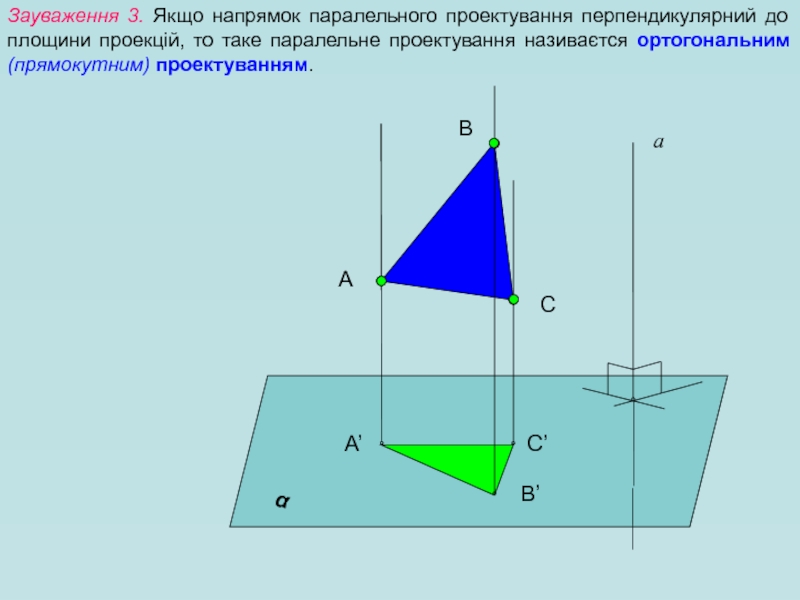
Зауваження 3. Якщо напрямок паралельного проектування перпендикулярний до площини проекцій, то
таке паралельне проектування називаєтся ортогональним(прямокутним) проектуванням.
А
а
α
B
C
А’
B’
C’
Слайд 9
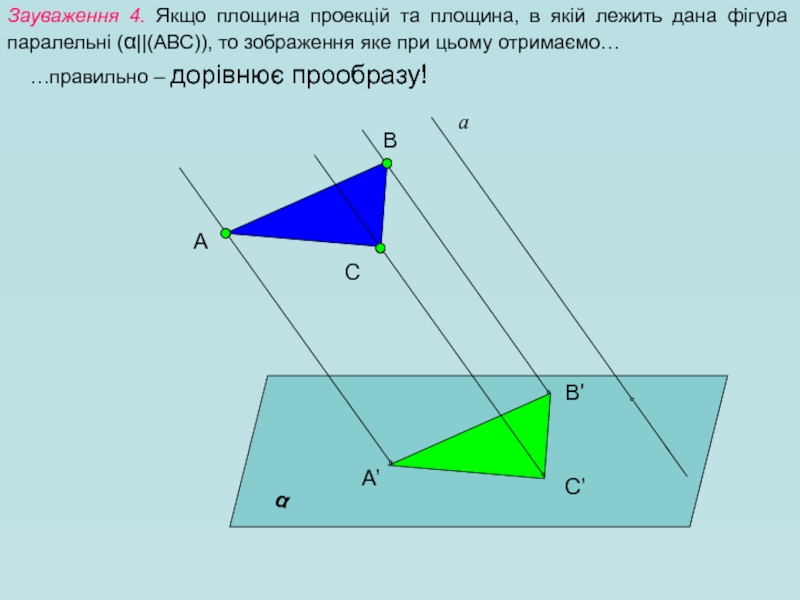
Зауваження 4. Якщо площина проекцій та площина, в якій лежить дана
фігура паралельні (α||(АВС)), то зображення яке при цьому отримаємо…
А
а
α
B
C
А’
B’
C’
…правильно – дорівнює прообразу!
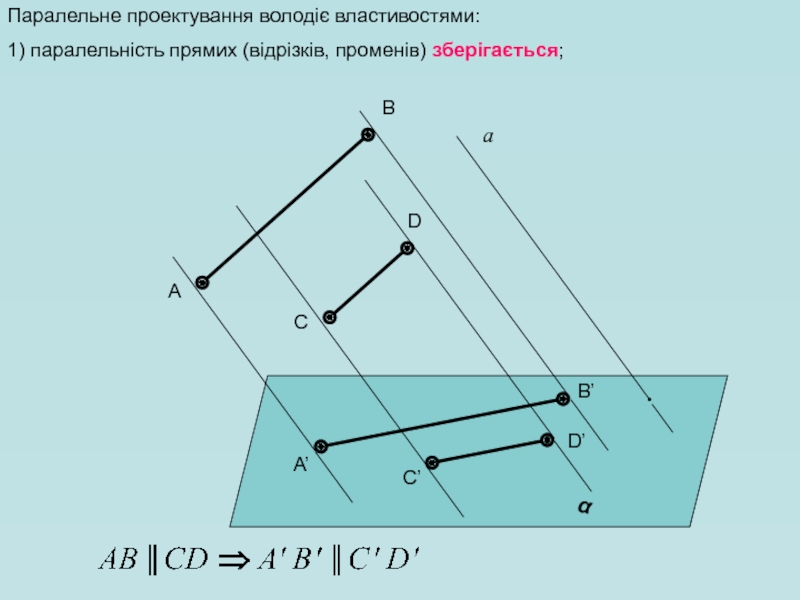
Слайд 10Паралельне проектування володіє властивостями:
1) паралельність прямих (відрізків, променів) зберігається;
α
а
A
D
C
B
A’
D’
C’
B’
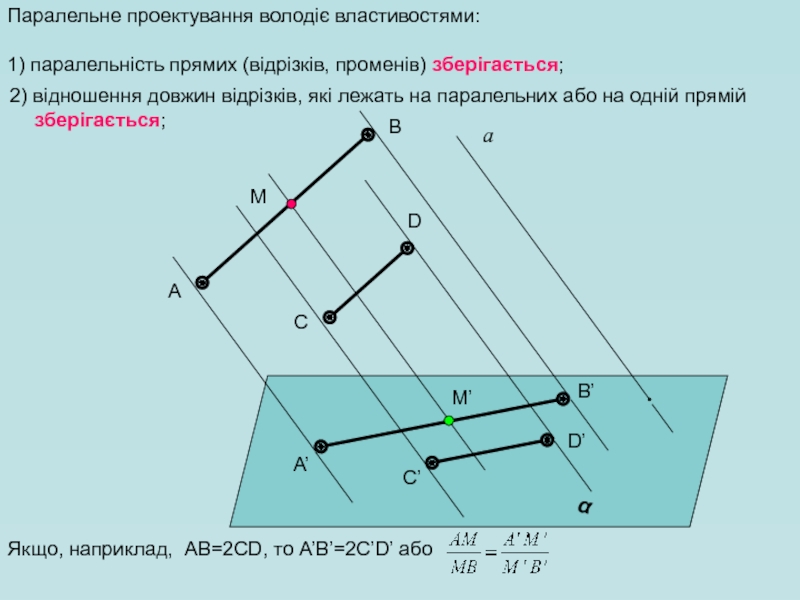
Слайд 11 2) відношення довжин відрізків, які лежать на паралельних або на
одній прямій зберігається;
Паралельне проектування володіє властивостями:
1) паралельність прямих (відрізків, променів) зберігається;
α
а
A
D
C
B
A’
D’
C’
B’
Якщо, наприклад, АВ=2CD, то А’В’=2C’D’ або
М
М’
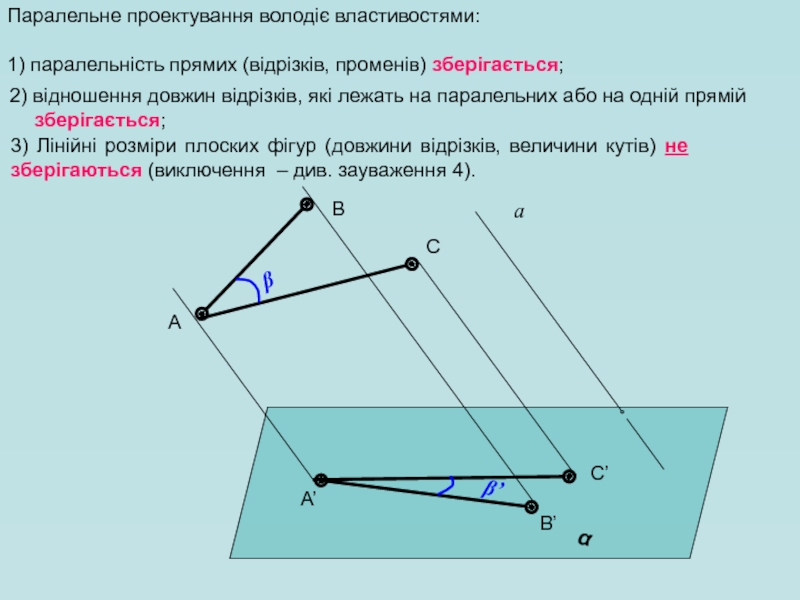
Слайд 12Паралельне проектування володіє властивостями:
1) паралельність прямих (відрізків, променів) зберігається;
α
а
A
B
A’
B’
3) Лінійні розміри
плоских фігур (довжини відрізків, величини кутів) не зберігаються (виключення – див. зауваження 4).
2) відношення довжин відрізків, які лежать на паралельних або на одній прямій зберігається;
β
β’
C
C’
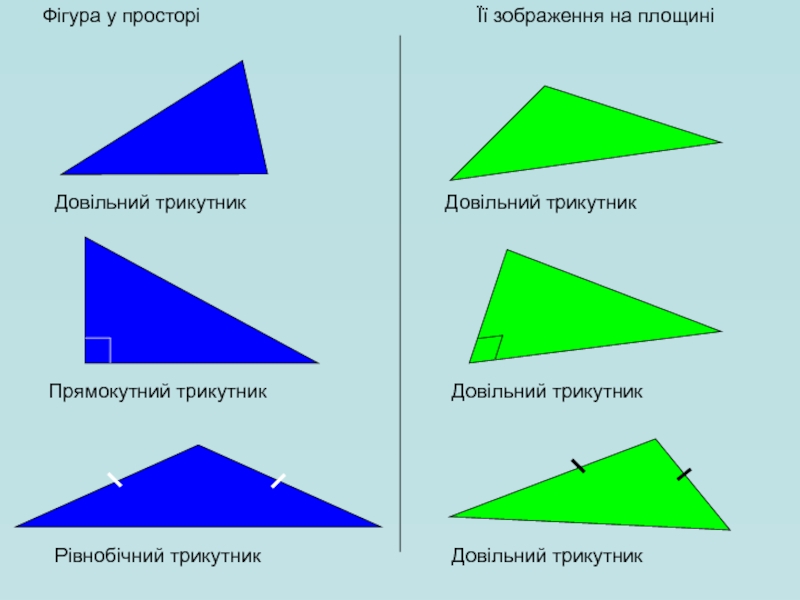
Слайд 14Фігура у просторі
Її зображення на площині
Довільний трикутник
Довільний трикутник
Прямокутний трикутник
Довільний
трикутник
Рівнобічний трикутник
Довільний трикутник
Слайд 15
Рівнобічний трикутник
Довільний трикутник
Паралелограм
Довільний паралелограм
Прямокутник
Довільний паралелограм
Фігура у просторі
Її зображення на
площині
Слайд 16Фігура у просторі
Її зображення на площині
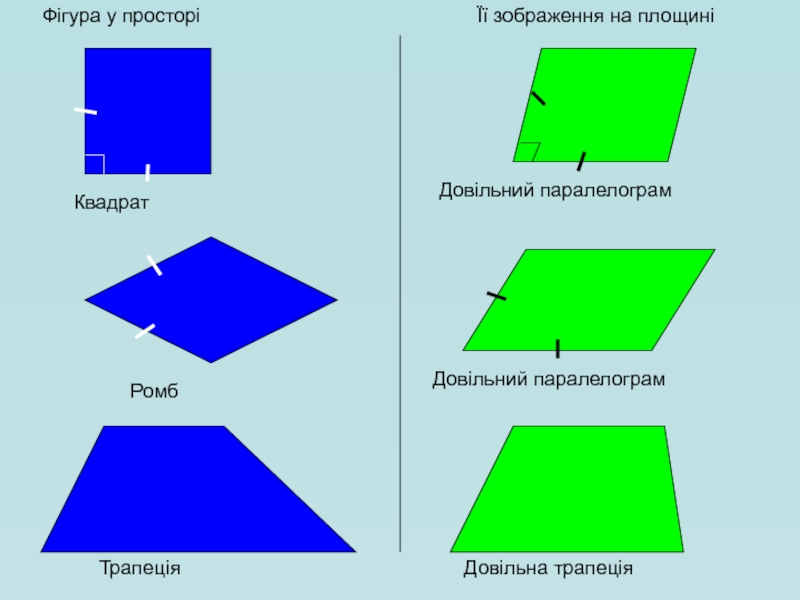
Квадрат
Довільний паралелограм
Трапеція
Довільна трапеція
Довільний паралелограм
Ромб
Слайд 17Фігура у просторі
Її зображення на площині
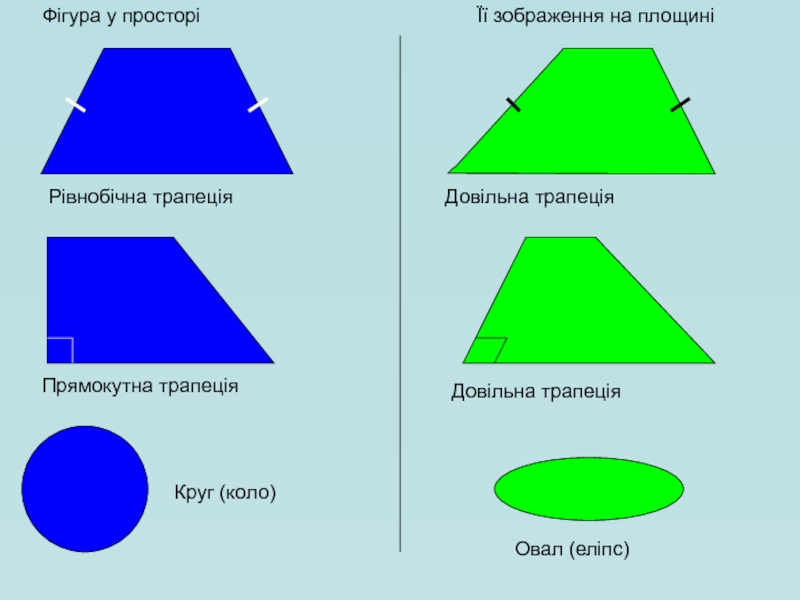
Рівнобічна трапеція
Довільна трапеція
Прямокутна трапеція
Довільна трапеція
Круг (коло)
Овал
(еліпс)
Слайд 18
A
B
C
D
E
F
O
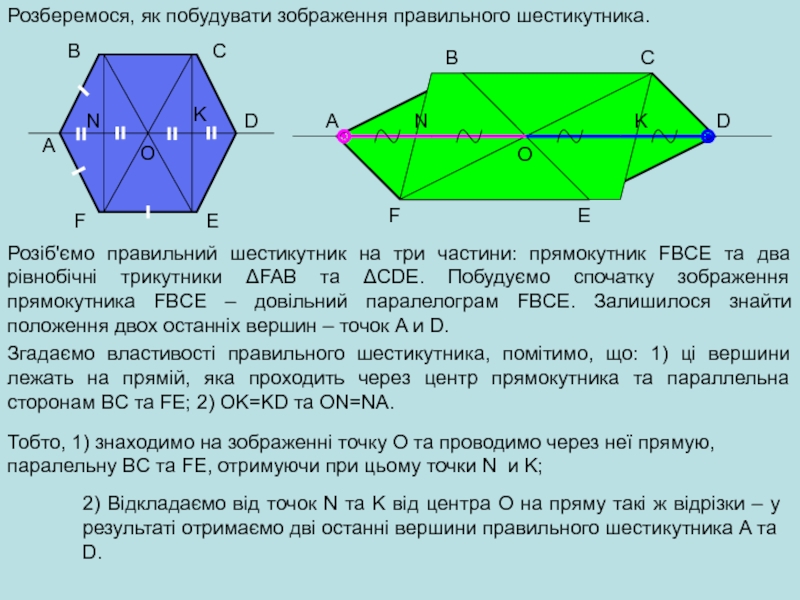
Розберемося, як побудувати зображення правильного шестикутника.
F
A
B
C
D
E
Розіб'ємо правильний шестикутник на три частини:
прямокутник FBCE та два рівнобічні трикутники ΔFAB та ΔCDE. Побудуємо спочатку зображення прямокутника FBCE – довільний паралелограм FBCE. Залишилося знайти положення двох останніх вершин – точок A и D.
Згадаємо властивості правильного шестикутника, помітимо, що: 1) ці вершини лежать на прямій, яка проходить через центр прямокутника та параллельна сторонам BC та FE; 2) OK=KD та ON=NA.
K
N
Тобто, 1) знаходимо на зображенні точку О та проводимо через неї прямую, паралельну BC та FE, отримуючи при цьому точки N и K;
O
N
K
2) Відкладаємо від точок N та K від центра О на пряму такі ж відрізки – у результаті отримаємо дві останні вершини правильного шестикутника A та D.
Слайд 19
A
B
C
D
E
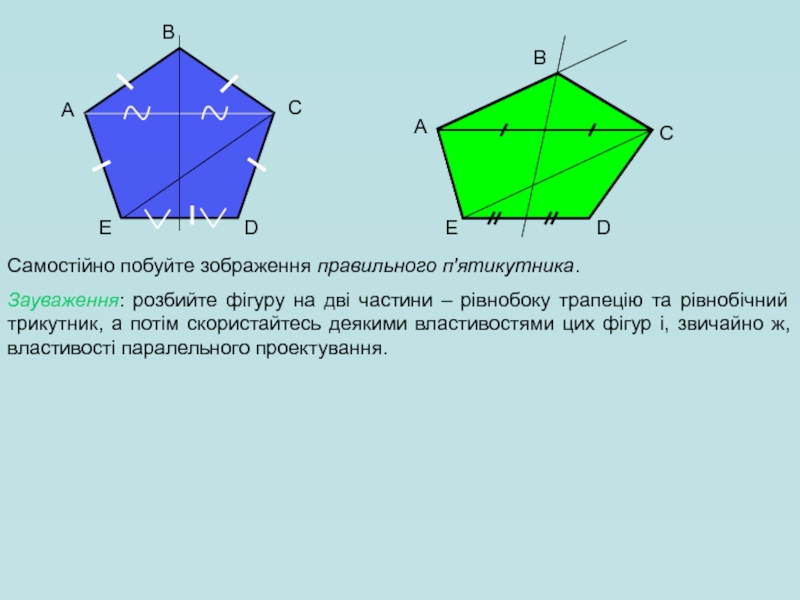
Самостійно побуйте зображення правильного п'ятикутника.
Зауваження: розбийте фігуру на дві частини –
рівнобоку трапецію та рівнобічний трикутник, а потім скористайтесь деякими властивостями цих фігур і, звичайно ж, властивості паралельного проектування.
A
C
D
E
B
