- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Отношения между множествами презентация
Содержание
- 1. Отношения между множествами
- 2. Отношения между множествами Пересечение множеств Непересечение множеств Включение множеств Равенство множеств Равномощность множеств
- 3. Пересечение множеств Если множества А
- 4. Непересечение множеств Если множества А
- 5. Отношение включения Если все элементы множества А
- 6. У любого множества есть два
- 7. Если множество А является подмножеством
- 8. Отношение равенства Если множество А
- 9. Отношение равномощности Если между элементами
Слайд 2Отношения между множествами
Пересечение множеств
Непересечение множеств
Включение множеств
Равенство множеств
Равномощность множеств
Слайд 3Пересечение множеств
Если множества А и В имеют некоторые общие
элементы, то эти множества находятся в отношении пересечения.
Пример.
А={3,4,6,8,9} и В= {3,5,2,8,1}
3 ∈ А, 8 ∈ А, 3 ∈ В, 8 ∈ В, но
4 ∈ А и 4∉В, 5 ∉ А и 5 ∈ В.
Пример.
А={3,4,6,8,9} и В= {3,5,2,8,1}
3 ∈ А, 8 ∈ А, 3 ∈ В, 8 ∈ В, но
4 ∈ А и 4∉В, 5 ∉ А и 5 ∈ В.
Слайд 4Непересечение множеств
Если множества А и В не имеют общих
элементов, то эти множества находятся в отношении непересечения.
Пример.
А={3,4,6,8,9}
и В= {7, 5, 2,1}
Пример.
А={3,4,6,8,9}
и В= {7, 5, 2,1}
Слайд 5Отношение включения
Если все элементы множества А являются элементами множества В, то
множество А называется подмножеством множества В.
У любого множества подмножеств, где n – количество элементов в данном множестве.
Пример. А={3,4,6,8,9} , n(А)=5 ⇒
В={3,4,6} , n(В)=3 ⇒
С={3} , n(С)=1 ⇒
У любого множества подмножеств, где n – количество элементов в данном множестве.
Пример. А={3,4,6,8,9} , n(А)=5 ⇒
В={3,4,6} , n(В)=3 ⇒
С={3} , n(С)=1 ⇒
Слайд 6 У любого множества есть два несобственных подмножества – пустое
множество и само множество.
Пример. Выпишите все возможные подмножества множества А, если А={3,4,6}.
Подмножества: В= {3}, С= {4}, D= {6}, Е= {3,4}, F= {3,6}, K= {4,6}, L= {3,4,6},
M = {∅} .
Пример. Выпишите все возможные подмножества множества А, если А={3,4,6}.
Подмножества: В= {3}, С= {4}, D= {6}, Е= {3,4}, F= {3,6}, K= {4,6}, L= {3,4,6},
M = {∅} .
Отношение включения
Слайд 7 Если множество А является подмножеством множества В, то эти
множества находятся в отношении включения.
Пример.
А={3,4} и В= {7,5,4,2,1,3}
3 ∈ А, 4 ∈ А, 3 ∈ В, 4∈ В
А⊂В
Пример.
А={3,4} и В= {7,5,4,2,1,3}
3 ∈ А, 4 ∈ А, 3 ∈ В, 4∈ В
А⊂В
Отношение включения
Слайд 8Отношение равенства
Если множество А содержится в множестве В и
множество В содержится в множестве А, то тогда и только тогда множество А равно множеству В.
А⊂В и В⊂А⇔А=В
Пример. А={3, 4, 1} и В={3, 1, 4}
А=В
А⊂В и В⊂А⇔А=В
Пример. А={3, 4, 1} и В={3, 1, 4}
А=В
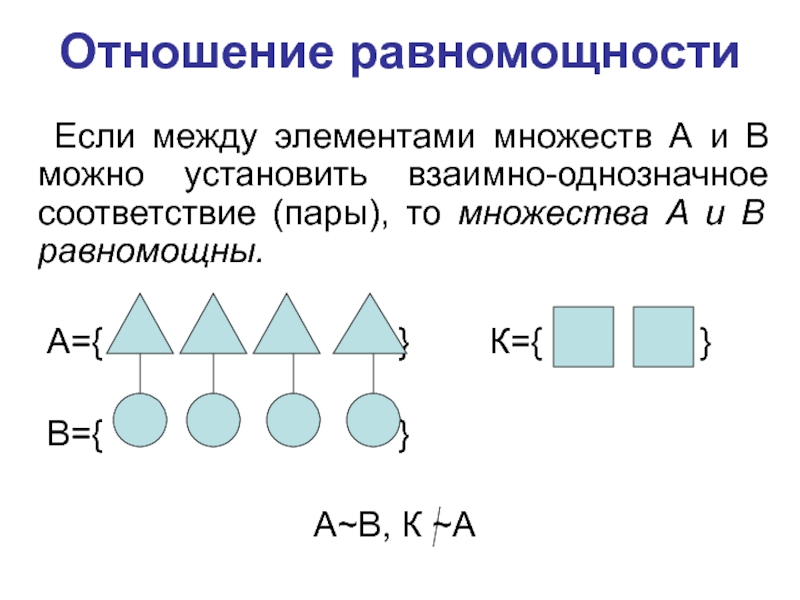
Слайд 9Отношение равномощности
Если между элементами множеств А и В можно
установить взаимно-однозначное соответствие (пары), то множества А и В равномощны.
А={ } К={ }
В={ }
А~В, К ~А
А={ } К={ }
В={ }
А~В, К ~А