- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы векторной алгебры. Векторы на плоскости и в пространстве презентация
Содержание
- 1. Основы векторной алгебры. Векторы на плоскости и в пространстве
- 2. 1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- 3. Опр. Вектор (в пространстве, на плоскости, на
- 4. Опр. Ненулевые векторы
- 5. Сложение векторов Пусть
- 6. 2. Разность векторов Опр. Разность векторов
- 7. 3. Умножение вектора на число Опр. Произведение
- 8. Опр. Два вектора
- 9. Первый признак коллинеарности двух ненулевых векторов (следует из определения)
- 10. Опр. Три вектора
- 11. Множество всех свободных векторов на прямой будем
- 12. Опр. 1) Базисом в пространстве называются любые
- 13. Опр. Если
- 14. Опр. Если
- 15. Опр. Векторы называются линейно зависимыми, если
- 16. Свойства Если среди векторов есть нулевой вектор,
- 17. 2. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
- 18. О – произвольная точка
- 19. Вектор заданный
- 20. Задача 1. Найти координаты вектора, если даны
- 21. Условие коллинеарности двух векторов Векторы
- 22. Длина вектора
- 23. Линейные операции над векторами в координатной форме
- 24. Направление вектора определяется углами α, β,
- 25. 3. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 26. Опр. Скалярным произведением двух
- 27. Задача. Даны векторы Найти: 1)
- 28. Задача. Даны векторы Найти: 2) Длина вектора:
- 29. Задача. Даны векторы Найти: 3)
- 30. Задача. Даны векторы Найти: 4)
- 31. Три некомпланарных вектора
- 32. Векторное произведение векторов Опр. Векторным произведением двух
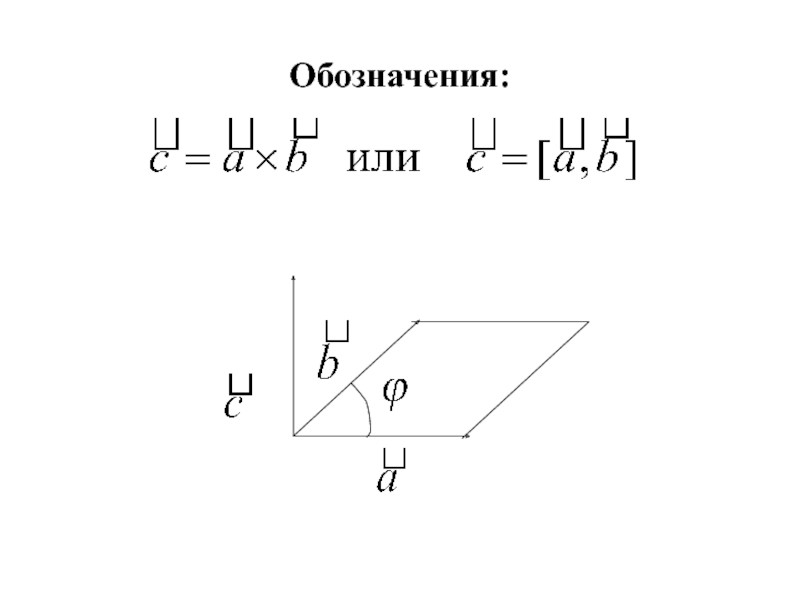
- 33. Обозначения:
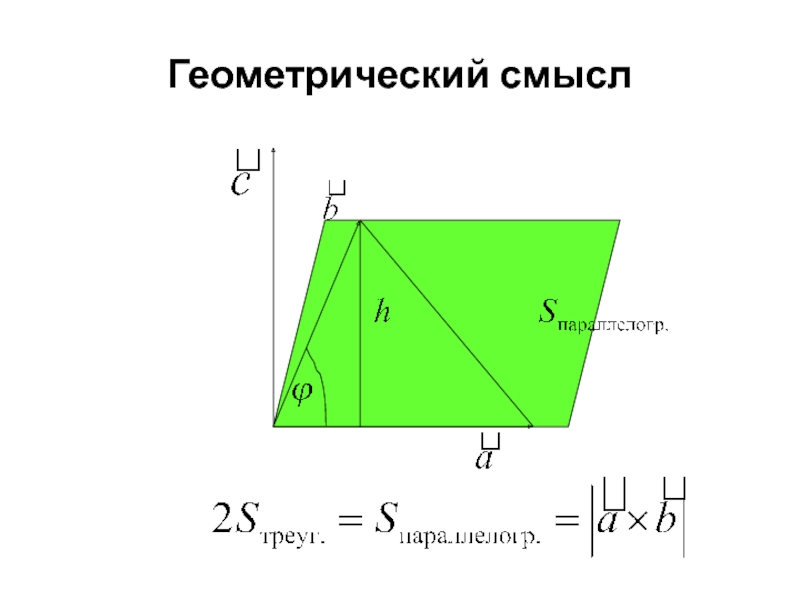
- 34. Геометрический смысл
- 35. Свойства
- 36. 6. Теорема (запись векторного произведения в координатах) Если
- 37. Смешанное произведение векторов Опр. Смешанным произведением трех
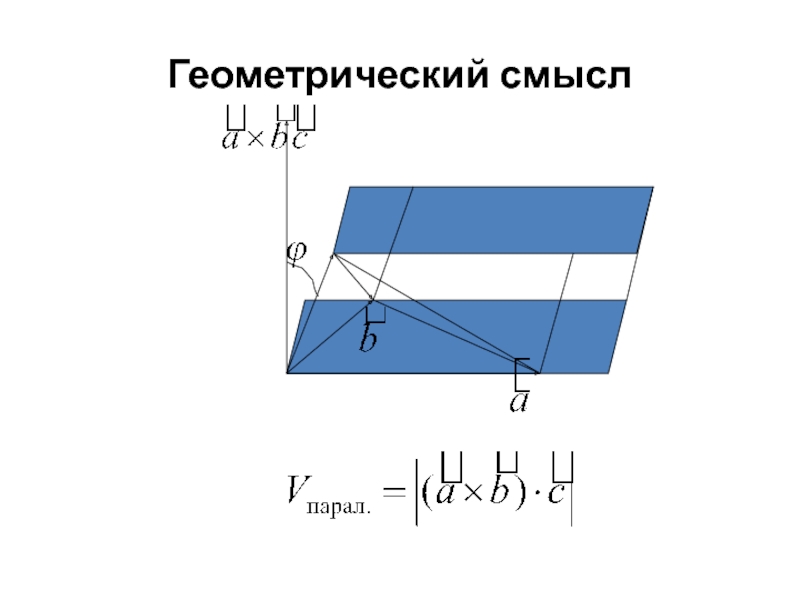
- 38. Геометрический смысл
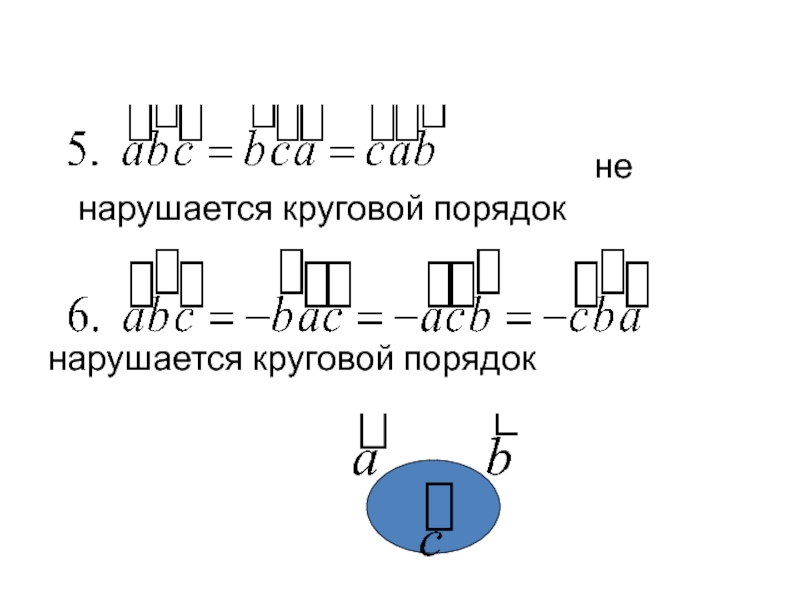
- 39. Свойства
- 41. 7. Теорема (запись смешанного произведения в координатах) Если
- 42. 8. Признак компланарности трех векторов (линейной зависимости
1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Слайд 3Опр. Вектор (в пространстве, на плоскости, на прямой) – это направленный
отрезок, т.е. отрезок AB, у которого одна из ограничивающих его точек A принимается за начало, а вторая B – за конец.
A
B
A
B
Слайд 4Опр. Ненулевые векторы
называются равными: , если:
они лежат на одной прямой или на параллельных прямых;
имеют одинаковые длины ( ) и одинаково направлены.
они лежат на одной прямой или на параллельных прямых;
имеют одинаковые длины ( ) и одинаково направлены.
A
B
C
D
Все нулевые векторы считаются равными друг другу.
Слайд 5Сложение векторов
Пусть - два произвольных вектора.
Возьмем произвольную точку О и приложим вектор к этой точке, получим .
Затем отложим от точки А вектор , получим . Вектор называется суммой векторов .
Затем отложим от точки А вектор , получим . Вектор называется суммой векторов .
Правило параллелограмма
Правило треугольника
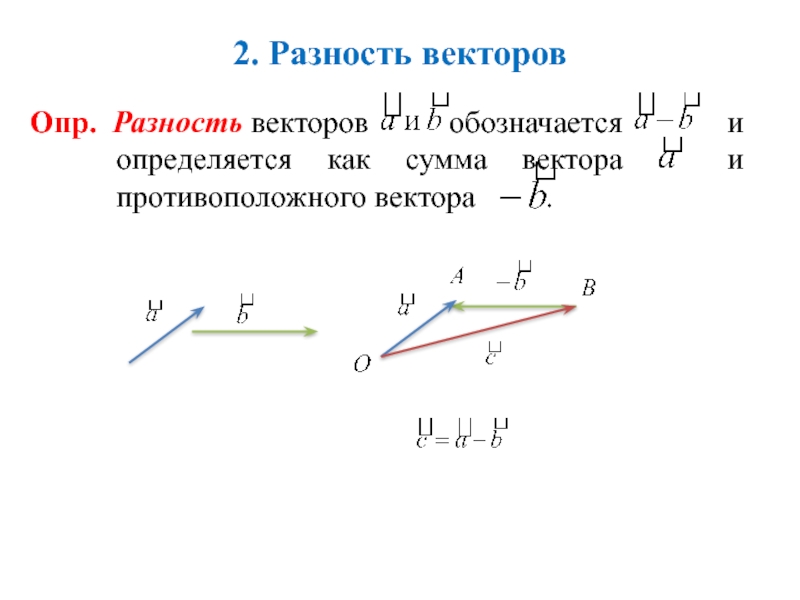
Слайд 62. Разность векторов
Опр. Разность векторов обозначается
и определяется как сумма вектора и противоположного вектора .
Слайд 73. Умножение вектора на число
Опр. Произведение вектора на число
λ называется вектор, длина которого равна числу и который имеет направление вектора , если λ > 0, и противоположное направление ( ), если λ < 0.
Обозначается: .
Если λ = 0 или , то .
Обозначается: .
Если λ = 0 или , то .
Слайд 8
Опр. Два вектора называются коллинеарными, если они
лежат на одной прямой или на параллельных прямых. В противном случае, они называются неколлинеарными.
Коллинеарные векторы
Неколлинеарные векторы
Нулевой вектор коллинеарен всякому вектору и каждый вектор коллинеарен самому себе.
Опр. Вектор называется коллинеарным прямой l, если этот вектор лежит либо на прямой l, либо прямой, параллельной l.
Слайд 10
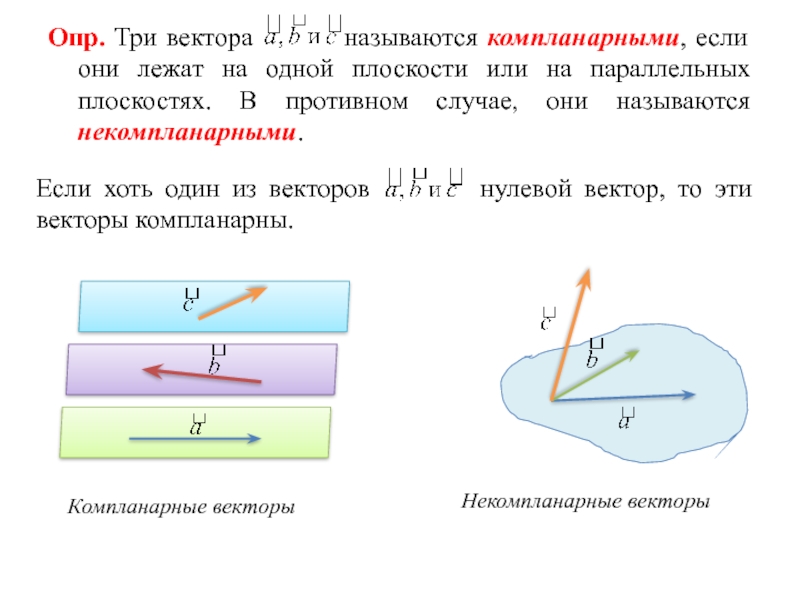
Опр. Три вектора называются компланарными, если они
лежат на одной плоскости или на параллельных плоскостях. В противном случае, они называются некомпланарными.
Если хоть один из векторов нулевой вектор, то эти векторы компланарны.
Компланарные векторы
Некомпланарные векторы
Слайд 11Множество всех свободных векторов на прямой будем обозначать R1, на плоскости
- R2, в пространстве - R3.
Опр. Множества R1, R2, R3 вместе с введёнными выше линейными операциями над векторами называются также векторными пространствами R1, R2, R3.
Опр. Множества R1, R2, R3 вместе с введёнными выше линейными операциями над векторами называются также векторными пространствами R1, R2, R3.
Слайд 12Опр.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в
определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарных вектора, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
2) Базисом на плоскости называются любые 2 неколлинеарных вектора, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Слайд 13
Опр. Если - базис в
пространстве и , то числа α, β и γ - называются компонентами или координатами вектора в этом базисе.
В связи с этим можно записать следующие свойства:
равные векторы имеют одинаковые координаты,
при умножении вектора на число его компоненты тоже умножаются на это число,
при сложении векторов складываются их соответствующие компоненты.
В связи с этим можно записать следующие свойства:
равные векторы имеют одинаковые координаты,
при умножении вектора на число его компоненты тоже умножаются на это число,
при сложении векторов складываются их соответствующие компоненты.
Слайд 14Опр. Если - некоторая
система векторов пространства R (R1, R2 или R3), тогда любой вектор вида называется линейной комбинацией векторов
некоторые действительные числа, называемые коэффициентами линейной комбинации.
Если какой-либо вектор представляется в виде линейной комбинации некоторых векторов, то говорят, что он разложен по этим векторам.
некоторые действительные числа, называемые коэффициентами линейной комбинации.
Если какой-либо вектор представляется в виде линейной комбинации некоторых векторов, то говорят, что он разложен по этим векторам.
Слайд 15Опр. Векторы называются линейно зависимыми, если существует такая линейная комбинация
, при не равных нулю одновременно αi , т.е. .
Если же только при αi = 0 выполняется равенство , то векторы называются линейно независимыми.
Если же только при αi = 0 выполняется равенство , то векторы называются линейно независимыми.
Слайд 16Свойства
Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.
Если
к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Любые 4 вектора линейно зависимы.
Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Любые 4 вектора линейно зависимы.
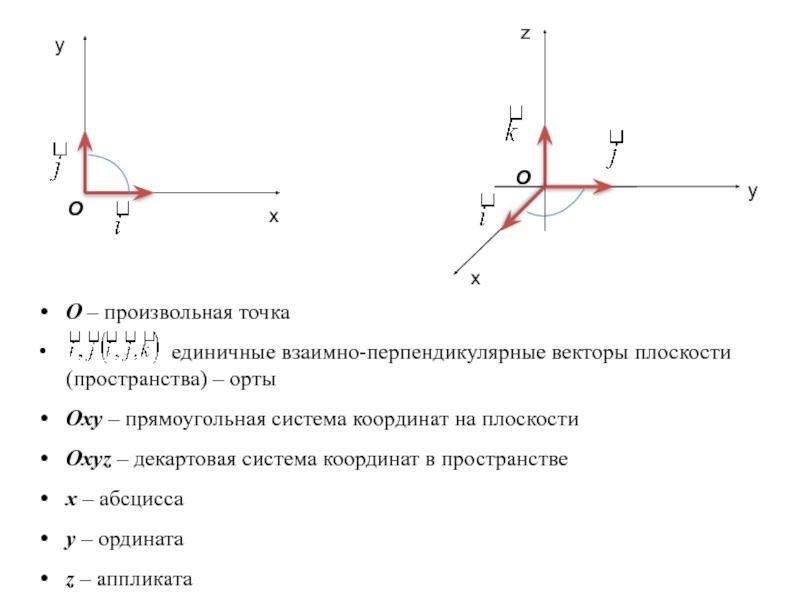
Слайд 18О – произвольная точка
единичные взаимно-перпендикулярные векторы плоскости (пространства) – орты
Oxy – прямоугольная система координат на плоскости
Oxyz – декартовая система координат в пространстве
x – абсцисса
y – ордината
z – аппликата
Oxy – прямоугольная система координат на плоскости
Oxyz – декартовая система координат в пространстве
x – абсцисса
y – ордината
z – аппликата
y
x
O
y
x
O
z
Слайд 19
Вектор заданный на плоскости Oxy, может быть представлен
в виде:
где x1, y1 – проекции вектора на соответствующие оси координат называются прямоугольными координатами вектора.
y
x
O
A(x1, y1)
y1
x1
Вектор с координатами x1 и y1 обозначается: и называется радиус-вектором точки А.
Слайд 20 Задача 1. Найти координаты вектора, если даны координаты его начальной и
конечной точек.
Решение.
Решение.
Слайд 21
Условие коллинеарности двух векторов
Векторы
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е. когда справедливо равенство
Слайд 24
Направление вектора определяется углами α, β, γ, образованными с осями координат
Ox, Oy, Oz.
Косинусы этих углов определяются по формулам:
Косинусы этих углов определяются по формулам:
Слайд 27Задача. Даны векторы
Найти: 1)
.
Разность двух векторов:
Скалярное произведение двух
векторов:
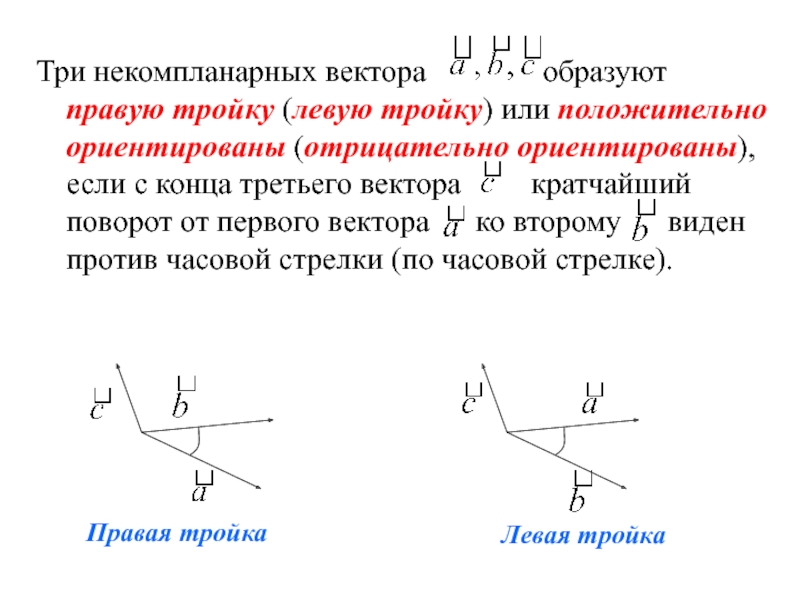
Слайд 31Три некомпланарных вектора образуют
правую тройку (левую тройку) или положительно ориентированы (отрицательно ориентированы), если с конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки (по часовой стрелке).
Правая тройка
Левая тройка
Слайд 32Векторное произведение векторов
Опр. Векторным произведением двух векторов
называется такой третий вектор , который удовлетворяет следующим трем условиям:
1) вектор ортогонален
2)
3) векторы образуют правую тройку.
Слайд 37Смешанное произведение векторов
Опр. Смешанным произведением трех векторов
называется число, обозначаемое и определяемое следующим образом
Слайд 428. Признак компланарности трех векторов (линейной зависимости трех векторов) Векторы
компланарны (линейно зависимы)
