- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неразрешимость исчисления предикатов презентация
Содержание
- 1. Неразрешимость исчисления предикатов
- 2. Проблема разрешимости Существует ли алгоритм,
- 3. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ НЕРАЗРЕШИМО
- 4. Доказательство Для
- 5. Машина Тьюринга M S={S0, S1,…,Sm} –
- 6. Предикатные формулы C(t,i,j) = “В момент
- 7. Предикатные формулы T(t) = “t является моментом
- 8. Предикатные формулы 3) T(t1)&T(t2)&T(s)&Nx(t1,s)& Nx(t2,s)
- 9. Предикатные формулы Sq(x) = “x является ячейкой
- 10. Предикатные формулы 2) Sq(x)⊃∃y(Sq(y)&L(x,y))&∀y1∀y2[Sq(y1)& &Sq(y2)&L(x,
- 11. Предикатные формулы 3) (L(x,y) ⊃ L*(x,y))
- 12. Характеристики МТ 1. В каждый
- 13. Характеристики МТ 5. Изменение состояния,
- 14. Построение формулы A A =
- 15. Построение формулы B B =
- 16. Построение формулы C C =
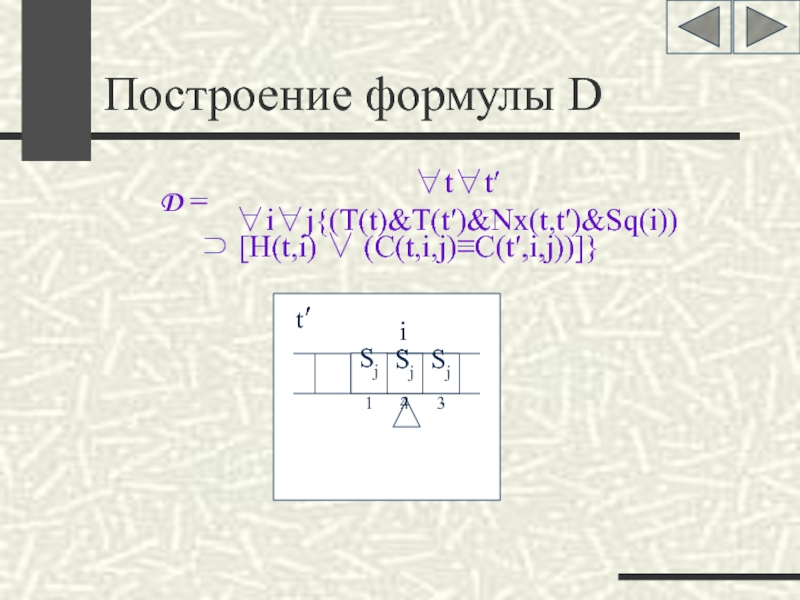
- 17. Построение формулы D i Sj2 Sj4 Sj3 Sj1 t t′
- 18. Построение формулы E Программа МТ
- 19. Построение формул F и G F
- 20. Построение формулы U(M) U(M)=A&B&C&D&E&F&G, т.е.
- 21. Лемма 1 Если МТ M останавливается, то U(M) выполнима.
- 22. Лемма 2 Если U(M) выполнима, то МТ M останавливается.
- 23. Доказательство леммы 1 МТ M
- 24. Доказательство леммы 2 Если мы
- 25. Доказательство неразрешимости Предположим, что исчисление
- 26. Чистое ИП x=y заменим
Слайд 2Проблема разрешимости
Существует ли алгоритм, позволяющий установить, выполнима данная формула
U исчисления предикатов или нет?
Слайд 4Доказательство
Для произвольной машины Тьюринга M мы построим
формулу U(M) и покажем, что если существует метод определения, выполнима ли U(M), то существует метод определения, остановится ли МТ M на данном слове.
Слайд 5Машина Тьюринга M
S={S0, S1,…,Sm} – внешний алфавит МТ M.
S0 = ‘Λ’
(пустой символ)
Q={q0, q1,…,qr} – внутренние состояния МТ M.
q1 – начальное состояние МТ M.
q0 – заключительное состояние МТ M.
Q={q0, q1,…,qr} – внутренние состояния МТ M.
q1 – начальное состояние МТ M.
q0 – заключительное состояние МТ M.
Слайд 6Предикатные формулы
C(t,i,j) = “В момент времени t в ячейке i
ленты МТ M находится символ Sj”.
H(t,i) = “В момент времени t обозревается ячейка i ленты МТ M”.
S(t,k) = “В момент времени t МТ M находится во внутреннем состоянии qk”.
H(t,i) = “В момент времени t обозревается ячейка i ленты МТ M”.
S(t,k) = “В момент времени t МТ M находится во внутреннем состоянии qk”.
Слайд 7Предикатные формулы
T(t) = “t является моментом времени”.
Nx(t,s) = “s следует непосредственно
за t”.
Аксиомы:
1) T(0) & ∀s[T(s) ⊃ ¬ Nx(s,0)]– существует некоторый начальный момент времени t = 0.
2) T(t)⊃∃s(T(s)&Nx(t,s))&∀s1∀s2[T(s1)&T(s2)& &Nx(t, s1)&Nx(t, s2) ⊃(s1=s2)] – для каждого момента времени существует единственный следующий.
Аксиомы:
1) T(0) & ∀s[T(s) ⊃ ¬ Nx(s,0)]– существует некоторый начальный момент времени t = 0.
2) T(t)⊃∃s(T(s)&Nx(t,s))&∀s1∀s2[T(s1)&T(s2)& &Nx(t, s1)&Nx(t, s2) ⊃(s1=s2)] – для каждого момента времени существует единственный следующий.
Слайд 8Предикатные формулы
3) T(t1)&T(t2)&T(s)&Nx(t1,s)& Nx(t2,s)
⊃(t1= t2)
4) (Nx(t,s) ⊃
Nx*(t,s)) &
(Nx*(t,s)& Nx*(s,r) ⊃ Nx*(t,r))&¬ Nx*(t,t))
– моменты времени идут последовательно друг за другом, т.е. невозможна ситуация:
(Nx*(t,s)& Nx*(s,r) ⊃ Nx*(t,r))&¬ Nx*(t,t))
– моменты времени идут последовательно друг за другом, т.е. невозможна ситуация:
Слайд 9Предикатные формулы
Sq(x) = “x является ячейкой ленты”.
L(x,y) = “x находится непосредственно
слева от y”.
Аксиомы:
1) Sq(1)&…&Sq(n)&L(1,2)&…&L(n-1,n) – существуют идущие друг за другом ячейки, в которых содержится начальное слово.
Аксиомы:
1) Sq(1)&…&Sq(n)&L(1,2)&…&L(n-1,n) – существуют идущие друг за другом ячейки, в которых содержится начальное слово.
Слайд 10Предикатные формулы
2) Sq(x)⊃∃y(Sq(y)&L(x,y))&∀y1∀y2[Sq(y1)&
&Sq(y2)&L(x, y1)&L(x, y2) ⊃(y1=y2)] – для каждой
ячейки существует единственная ячейка, находящаяся справа от нее.
Sq(x)⊃∃y(Sq(y)&L(y,x))&∀y1∀y2[Sq(y1)&
&Sq(y2)&L(y1,x)&L(y2,x) ⊃(y1=y2)] – для каждой ячейки существует единственная ячейка, находящаяся слева от нее.
Sq(x)⊃∃y(Sq(y)&L(y,x))&∀y1∀y2[Sq(y1)&
&Sq(y2)&L(y1,x)&L(y2,x) ⊃(y1=y2)] – для каждой ячейки существует единственная ячейка, находящаяся слева от нее.
Слайд 12Характеристики МТ
1. В каждый момент времени головка обозревает ровно
одну ячейку (= A).
2. В каждый момент времени в каждой ячейке ленты МТ стоит ровно один символ (= B).
3. В каждый момент времени МТ находится ровно в одном состоянии (= C).
4. При переходе от одного момента времени к другому может изменяться только содержимое обозреваемой ячейки (= D).
2. В каждый момент времени в каждой ячейке ленты МТ стоит ровно один символ (= B).
3. В каждый момент времени МТ находится ровно в одном состоянии (= C).
4. При переходе от одного момента времени к другому может изменяться только содержимое обозреваемой ячейки (= D).
Слайд 13Характеристики МТ
5. Изменение состояния, положения головки и содержимого ячейки
при переходе от одного момента времени к другому происходит в соответствии с программой МТ (= E).
6. Нулевой момент времени является начальным (= F).
7. Существует некоторый заключительный момент времени (= G).
6. Нулевой момент времени является начальным (= F).
7. Существует некоторый заключительный момент времени (= G).
Слайд 14Построение формулы A
A = ∀t (T(t) ⊃ At(t)),
где At(t) = “В момент времени t головка обозревает ровно одну клетку”.
At(t) =
∃i(Sq(i)& H(t,i))
&∀x∀y{(Sq(x)&Sq(y))⊃[(x=y)
∨ ¬(H(t,x)&H(t,y))]}
Слайд 15Построение формулы B
B = ∀t∀i [(T(t)&Sq(i)) ⊃ Bti(t,i)],
где Bti(t,i) = “В момент времени t в i-й ячейке ленты ровно один символ”.
Bti(t,i) =
Слайд 16Построение формулы C
C = ∀t (T(t) ⊃ Ct(t)),
где Ct(t) = “В момент времени t МТ находится ровно в одном состоянии”.
Сt(t) =
Слайд 18Построение формулы E
Программа МТ состоит из инструкций вида {qiSjSkLqm},
{qiSjSkRqm}, {qiSjSkNqm}.
⊃ [C(t′,x,k)&
qi
qm
t
t′
&S(t′,m)]}
Слайд 19Построение формул F и G
F = S(0,1)&H(0,1)&
&C(0,1,Sj1)&…&C(0,n,Sjn)&∀i(Sq(i)⊃
[(i=1)∨…∨(i=n)∨C(0,i,0)])
G = ∃t′
S(t′,0)
Слайд 20Построение формулы U(M)
U(M)=A&B&C&D&E&F&G,
т.е. формула U(M) соответствует МТ M, удовлетворяющей
приведенным ранее характеристикам.
Слайд 23Доказательство леммы 1
МТ M по определению удовлетворяет первым шести
характеристикам, т.е. можно найти такое присвоение значений 0 и 1 предикатным формулам H, S, C и т.д., что формулы A, B, C, D, E, F истинны.
По условию леммы МТ M останавливается, т.е. в некоторый момент времени t′ приходит в заключительное состояние q0. Следовательно, формула G истинна.
Тогда формула U(M) тоже истинна.
По условию леммы МТ M останавливается, т.е. в некоторый момент времени t′ приходит в заключительное состояние q0. Следовательно, формула G истинна.
Тогда формула U(M) тоже истинна.
Слайд 24Доказательство леммы 2
Если мы в выполнимой формуле в предикатные
формулы подставим некоторые значения, мы получим истинное высказывание. В частности, если мы подставим значения в формулу U(M), мы получим истинное предложение
“В некоторый момент времени МТ M останавливается”.
“В некоторый момент времени МТ M останавливается”.
Слайд 25Доказательство неразрешимости
Предположим, что исчисление предикатов разрешимо. Тогда существует машина
Тьюринга для определения выполнимости U(M). По леммам 1 и 2 получаем, что существует машина, определяющая остановится ли машина M. Это невозможно. Следовательно, исчисление предикатов неразрешимо!
Слайд 26Чистое ИП
x=y заменим предикатом Eq(x,y), для которого определим
аксиомы:
1) Eq(x,x).
2) (Eq(x,y)&Eq(y,z)) ⊃ Eq(x,z).
3) Eq(x,y) ⊃ Eq(y,x).
4) Eq(x1,y1)&…& Eq(xn,yn) ⊃
(P(x1,…,xn) ≡ P(y1,…,yn)) для каждого введенного предиката (P – предикатный символ)
Тогда получим доказательство для чистого ИП.
1) Eq(x,x).
2) (Eq(x,y)&Eq(y,z)) ⊃ Eq(x,z).
3) Eq(x,y) ⊃ Eq(y,x).
4) Eq(x1,y1)&…& Eq(xn,yn) ⊃
(P(x1,…,xn) ≡ P(y1,…,yn)) для каждого введенного предиката (P – предикатный символ)
Тогда получим доказательство для чистого ИП.









![Предикатные формулы2) Sq(x)⊃∃y(Sq(y)&L(x,y))&∀y1∀y2[Sq(y1)& &Sq(y2)&L(x, y1)&L(x, y2) ⊃(y1=y2)] – для каждой ячейки существует единственная ячейка, находящаяся](/img/tmb/5/494546/4078db8d1a11ff4435864dd94f224834-800x.jpg)




![Построение формулы B B = ∀t∀i [(T(t)&Sq(i)) ⊃ Bti(t,i)], где Bti(t,i) = “В момент времени](/img/tmb/5/494546/c2e8f4d27dd356014d0f10a84ccdb643-800x.jpg)

![Построение формулы E Программа МТ состоит из инструкций вида {qiSjSkLqm}, {qiSjSkRqm}, {qiSjSkNqm}.⊃ [C(t′,x,k)&qiqmtt′ &S(t′,m)]}](/img/tmb/5/494546/c092b8a9c18995b6a334b4ce3de67a2c-800x.jpg)
![Построение формул F и GF = S(0,1)&H(0,1)& &C(0,1,Sj1)&…&C(0,n,Sjn)&∀i(Sq(i)⊃[(i=1)∨…∨(i=n)∨C(0,i,0)]) G = ∃t′ S(t′,0)](/img/tmb/5/494546/389467ea8701d93c5e89803b140d9e37-800x.jpg)












