- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории вероятностей. (Лекция 1) презентация
Содержание
- 1. Основы теории вероятностей. (Лекция 1)
- 2. 07/30/2019 Харламова Ирина Юрьевна ЭЛЕМЕНТЫ КОМБИНАТОРИКИ 1.
- 3. 07/30/2019 Харламова Ирина Юрьевна Комбинаторика –
- 4. 07/30/2019 Харламова Ирина Юрьевна Комбинаторика возникла в
- 5. 07/30/2019 Харламова Ирина Юрьевна Теоретические исследования вопросов
- 6. 07/30/2019 Харламова Ирина Юрьевна Яков Бернулли (1654-1705) Готфрид Лейбниц (1646-1716) Леонард Эйлер (1707-1783)
- 7. 1 ? ОБЩИЕ ПРАВИЛА КОМБИНАТОРИКИ
- 8. 07/30/2019 Харламова Ирина Юрьевна ПРАВИЛО СУММЫ
- 9. 07/30/2019 Харламова Ирина Юрьевна ТУРЦИЯ
- 10. 07/30/2019 Харламова Ирина Юрьевна ЕГИПЕТ
- 11. 07/30/2019 Харламова Ирина Юрьевна
- 12. 07/30/2019 Харламова Ирина Юрьевна ПРАВИЛО ПРОИЗВЕДЕНИЯ
- 13. 07/30/2019 Харламова Ирина Юрьевна ТУРЦИЯ
- 14. 07/30/2019 Харламова Ирина Юрьевна ЕГИПЕТ
- 15. 07/30/2019 Харламова Ирина Юрьевна
- 16. 07/30/2019 Харламова Ирина Юрьевна
- 17. 07/30/2019 Харламова Ирина Юрьевна Правило суммы 2 4
- 18. 07/30/2019 Харламова Ирина Юрьевна 6
- 19. 07/30/2019 Харламова Ирина Юрьевна Правило произведения 4 2
- 20. 07/30/2019 Харламова Ирина Юрьевна
- 21. 2? Выборки элементов Размещения Сочетания Перестановки
- 22. 07/30/2019 Харламова Ирина Юрьевна Размещения Размещениями из
- 23. 07/30/2019 Харламова Ирина Юрьевна a, b, c составом
- 24. 07/30/2019 Харламова Ирина Юрьевна Число размещений из n элементов по k
- 25. 07/30/2019 Харламова Ирина Юрьевна Число размещений из 3 элементов по 2
- 26. 07/30/2019 Харламова Ирина Юрьевна a, b, c составом
- 27. 07/30/2019 Харламова Ирина Юрьевна В турнире по
- 28. 07/30/2019 Харламова Ирина Юрьевна A B
- 29. 07/30/2019 Харламова Ирина Юрьевна
- 30. 07/30/2019 Харламова Ирина Юрьевна
- 31. 07/30/2019 Харламова Ирина Юрьевна n=k Соответствующие этому случаю размещения называют перестановками.
- 32. 07/30/2019 Харламова Ирина Юрьевна Перестановки Перестановками из
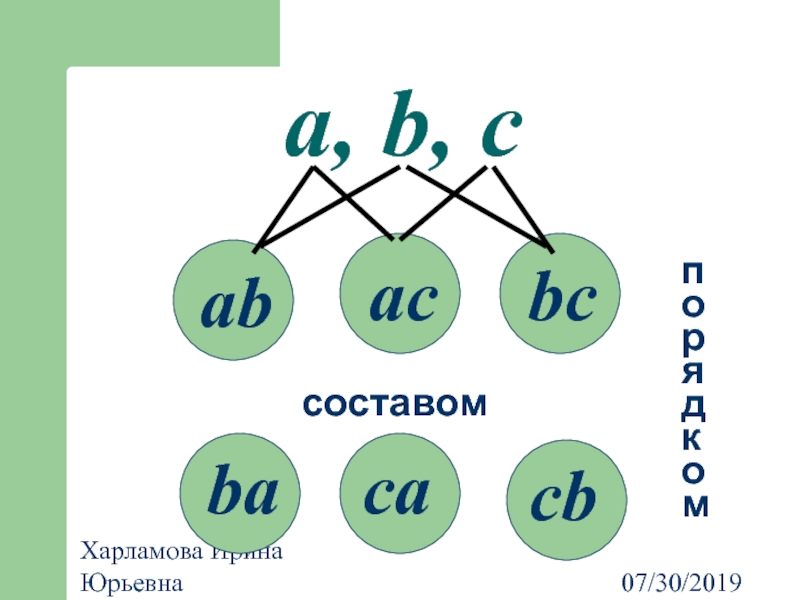
- 33. 07/30/2019 Харламова Ирина Юрьевна a, b, c п о р я д к о м
- 34. 07/30/2019 Харламова Ирина Юрьевна Число перестановок из n элементов
- 35. 07/30/2019 Харламова Ирина Юрьевна Число перестановок из n элементов
- 36. 07/30/2019 Харламова Ирина Юрьевна Число перестановок из 3 элементов
- 37. 07/30/2019 Харламова Ирина Юрьевна a, b, c п о р я д к о м
- 38. 07/30/2019 Харламова Ирина Юрьевна
- 39. 07/30/2019 Харламова Ирина Юрьевна Сколько перестановок можно сделать из букв слова ЮРИСТ
- 40. 07/30/2019 Харламова Ирина Юрьевна ю и ю р и с т р ю
- 41. 07/30/2019 Харламова Ирина Юрьевна Число перестановок из 5 элементов
- 42. 07/30/2019 Харламова Ирина Юрьевна Сочетания Сочетаниями из
- 43. 07/30/2019 Харламова Ирина Юрьевна a, b, c с о с т а в о м
- 44. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний из n элементов по k
- 45. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний из 3 элементов по 2
- 46. 07/30/2019 Харламова Ирина Юрьевна На тренировке занимаются
- 47. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний из 15 элементов по 5
- 48. 3? Выборки с повторениями Размещения с повторениями Сочетания с повторениями Перестановки с повторениями
- 49. 07/30/2019 Харламова Ирина Юрьевна Размещения с повторениями
- 50. 07/30/2019 Харламова Ирина Юрьевна a, b, c
- 51. 07/30/2019 Харламова Ирина Юрьевна Число размещений с
- 52. 07/30/2019 Харламова Ирина Юрьевна Число размещений с
- 53. 07/30/2019 Харламова Ирина Юрьевна a, b, c
- 54. 07/30/2019 Харламова Ирина Юрьевна Код Морзе
- 55. 07/30/2019 Харламова Ирина Юрьевна С помощью одного
- 56. 07/30/2019 Харламова Ирина Юрьевна С помощью трех
- 57. 07/30/2019 Харламова Ирина Юрьевна В русском алфавите
- 58. 07/30/2019 Харламова Ирина Юрьевна Перестановки с повторениями
- 59. 07/30/2019 Харламова Ирина Юрьевна в которых есть
- 60. 07/30/2019 Харламова Ирина Юрьевна Сколько перестановок можно сделать из букв слова ПРОКУРОР
- 61. 07/30/2019 Харламова Ирина Юрьевна ПРОКУРОР ПРОКУРОР Р Р ПРОКУРОР ПРОКУРОР Р Р Р К
- 62. 07/30/2019 Харламова Ирина Юрьевна n=8: ПРОКУРОР
- 63. 07/30/2019 Харламова Ирина Юрьевна
- 64. 07/30/2019 Харламова Ирина Юрьевна АНАГРАММЫ
- 65. 07/30/2019 Харламова Ирина Юрьевна АРХИМЕД (ок. 287 – 212 до н.э.)
- 66. 07/30/2019 Харламова Ирина Юрьевна АНАГРАММЫ СОСНА НАСОС
- 67. 07/30/2019 Харламова Ирина Юрьевна Христиан Гюйгенс
- 68. 07/30/2019 Харламова Ирина Юрьевна «Окружен кольцом тонким,
- 69. 07/30/2019 Харламова Ирина Юрьевна Христиан Гюйгенс
- 70. 07/30/2019 Харламова Ирина Юрьевна
- 71. 07/30/2019 Харламова Ирина Юрьевна ≈1060
- 72. 07/30/2019 Харламова Ирина Юрьевна Сочетания с повторениями
- 73. 07/30/2019 Харламова Ирина Юрьевна a, b, c
- 74. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний с
- 75. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний с
- 76. 07/30/2019 Харламова Ирина Юрьевна a, b, c
- 77. 07/30/2019 Харламова Ирина Юрьевна В гастрономе
- 78. 07/30/2019 Харламова Ирина Юрьевна
- 79. 07/30/2019 Харламова Ирина Юрьевна
- 80. 07/30/2019 Харламова Ирина Юрьевна Число сочетаний с
- 81. 07/30/2019 Харламова Ирина Юрьевна 5×7=35
- 82. 07/30/2019 Харламова Ирина Юрьевна
- 83. 07/30/2019 Харламова Ирина Юрьевна Число, положение
07/30/2019 Харламова Ирина Юрьевна ЭЛЕМЕНТЫ КОМБИНАТОРИКИ 1. Общие правила комбинаторики. 2. Выборки элементов. 3. Выборки элементов с повторениями.
Слайд 207/30/2019
Харламова Ирина Юрьевна
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
1. Общие правила комбинаторики.
2. Выборки элементов.
3. Выборки элементов
с повторениями.
Слайд 307/30/2019
Харламова Ирина Юрьевна
Комбинаторика –
область математики, в которой изучаются вопросы
о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.
Слайд 407/30/2019
Харламова Ирина Юрьевна
Комбинаторика возникла в XVI веке. В жизни привилегированных слоев
тогдашнего общества большое место занимали азартные игры.
Слайд 507/30/2019
Харламова Ирина Юрьевна
Теоретические исследования вопросов комбинаторики предприняли в XVII веке французские ученые
Пьер Ферма
(1601-65)
Блез Паскаль
(1623-62)
Слайд 607/30/2019
Харламова Ирина Юрьевна
Яков Бернулли
(1654-1705)
Готфрид Лейбниц
(1646-1716)
Леонард Эйлер
(1707-1783)
Слайд 807/30/2019
Харламова Ирина Юрьевна
ПРАВИЛО СУММЫ
Если некоторый объект А можно выбрать
m способами, а другой объект В можно выбрать k способами, то выбор
«либо А, либо В»
можно осуществить m+k способами.
«либо А, либо В»
можно осуществить m+k способами.
Слайд 1207/30/2019
Харламова Ирина Юрьевна
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Если объект А можно выбрать m
способами, и если после каждого такого выбора объект В можно выбрать k способами, то выбор пары объектов
А и В
в указанном порядке можно осуществить
m⋅k способами.
А и В
в указанном порядке можно осуществить
m⋅k способами.
Слайд 2207/30/2019
Харламова Ирина Юрьевна
Размещения
Размещениями из n элементов по k называются такие выборки,
которые, имея по k различных элементов, выбранных из числа данных n, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Слайд 2707/30/2019
Харламова Ирина Юрьевна
В турнире по футболу участвуют 18 команд. Борьба идет
за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
Слайд 3107/30/2019
Харламова Ирина Юрьевна
n=k
Соответствующие этому случаю размещения называют перестановками.
Слайд 3207/30/2019
Харламова Ирина Юрьевна
Перестановки
Перестановками из n элементов называются такие выборки, которые, имея
по n различных элементов, отличаются одна от другой лишь порядком следования этих элементов.
Слайд 4207/30/2019
Харламова Ирина Юрьевна
Сочетания
Сочетаниями из n элементов по k называются такие выборки,
которые, имея по k различных элементов, выбранных из числа данных n, отличаются только составом элементов (порядок расположения элементов значения не имеет).
Слайд 4607/30/2019
Харламова Ирина Юрьевна
На тренировке занимаются 15 баскетболистов. Сколько может быть образовано
тренером разных стартовых пятерок?
Слайд 483? Выборки с повторениями
Размещения с повторениями
Сочетания с повторениями
Перестановки с повторениями
Слайд 4907/30/2019
Харламова Ирина Юрьевна
Размещения с повторениями
из n элементов по k
Размещениями
с повторениями из n элементов по k называются такие выборки, которые, имея по k элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения, причем один и тот же элемент может входить в выборку более одного раза.
Слайд 5407/30/2019
Харламова Ирина Юрьевна
Код Морзе
Самуэль Морзе
(1791-1872)
При передачи сообщений по телеграфу используется код
Морзе. В этом коде буквы, цифры и знаки препинания обозначаются точками и тире.
Можно ли передавать сообщение с помощью четырех знаков?
Можно ли передавать сообщение с помощью четырех знаков?
Слайд 5507/30/2019
Харламова Ирина Юрьевна
С помощью одного знака можно передать только
2 буквы:
С
помощью двух знаков можно передать 4 буквы:
• •
• –
– •
– –
Слайд 5607/30/2019
Харламова Ирина Юрьевна
С помощью трех знаков можно передать 8 букв:
С помощью
четырех знаков можно передать 16 букв:
Слайд 5707/30/2019
Харламова Ирина Юрьевна
В русском алфавите 33 буквы, также надо передавать цифры
и знаки препинания .
Следовательно, 4 знаков не хватит.
Следовательно, 4 знаков не хватит.
30+32=62
Э••–• •
Слайд 5807/30/2019
Харламова Ирина Юрьевна
Перестановки с повторениями
Перестановки, в которых хоть
один элемент встречается более одного раза, называются перестановками с повторениями.
Слайд 5907/30/2019
Харламова Ирина Юрьевна
в которых есть n1 элементов одного вида, n2 элементов
другого вида и т.д.
Число перестановок с повторениями из n элементов,
Слайд 6407/30/2019
Харламова Ирина Юрьевна
АНАГРАММЫ
До XVII столетия почти не было научных
журналов. Ученые узнавали о трудах своих коллег или из книг, или из частных писем.
Слайд 6707/30/2019
Харламова Ирина Юрьевна
Христиан Гюйгенс
(1629-1695)
aaaaaaa, ccccc, d, eeeee, g, h,
iiiiiii, lll, mm, nnnnnnnnn, oooo, pp, q, rr, s, ttttt, uuuuu.
Слайд 6807/30/2019
Харламова Ирина Юрьевна
«Окружен кольцом тонким, плоским, нигде не подвешенным, наклонным к
эклиптике»
«Annulo cingitur tenui, plano, nusquam cohaerente, ad eclipticam inclinato»
Слайд 6907/30/2019
Харламова Ирина Юрьевна
Христиан Гюйгенс
(1629-1695)
aaaaaaa, ccccc, d, eeeee, g, h,
iiiiiii, lll, mm, nnnnnnnnn, oooo, pp, q, rr, s, ttttt, uuuuu.
Слайд 7207/30/2019
Харламова Ирина Юрьевна
Сочетания с повторениями
из n элементов по k
Сочетаниями
с повторениями из n элементов по k называются такие выборки, которые, имея по k элементов, выбранных из числа данных n элементов, отличаются друг от друга только составом элементов (порядок расположения элементов значения не имеет), причем один и тот же элемент может входить в выборку более одного раза.
Слайд 7707/30/2019
Харламова Ирина Юрьевна
В гастрономе
имеются подарочные
коробки конфет четырех
наименований. Сколькими
способами можно заказать набор из 5 коробок?
Слайд 8307/30/2019
Харламова Ирина Юрьевна
Число, положение
и комбинация - три
взаимно пересекающиеся,
но
различные сферы мысли,
к которым можно отнести все математические идеи.
Дж. Сильвестр (1844 г.)
