- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории фракталов презентация
Содержание
- 1. Основы теории фракталов
- 2. Геометрия природы Рождение фрактальной геометрии принято связывать
- 3. Природные фракталы
- 4. Размерность и самоподобие fractus (лат.) — дробленый, сломанный, разбитый
- 5. Патологические структуры Кривая Коха Описана в 1904 году Нигде не дифференцируема и не спрямляема
- 6. Определение Фрактал (лат. fractus — дробленый, сломанный,
- 7. Свойства Самоподобие Дробная размерность (в смысле Минковского или Хаусдорфа)
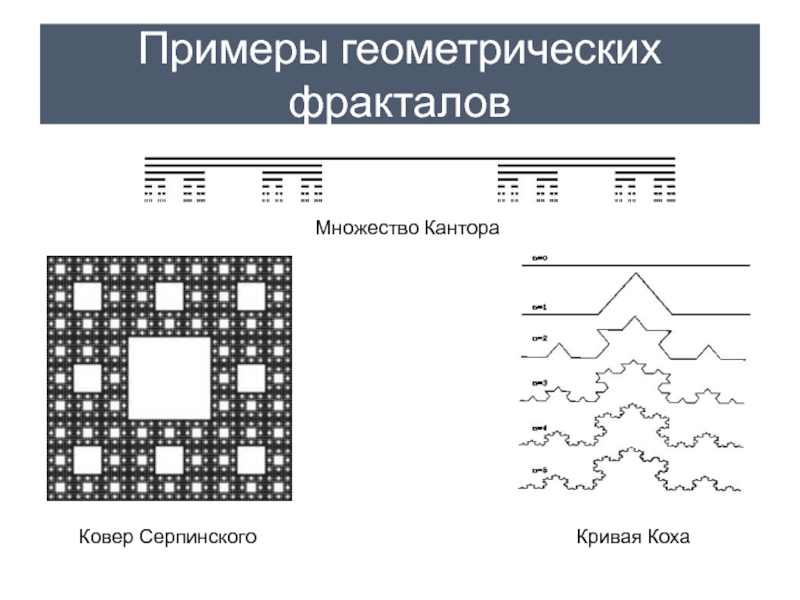
- 8. Геометрические фракталы Самые наглядные В двумерном
- 9. Примеры геометрических фракталов Множество Кантора Кривая Коха Ковер Серпинского
- 10. Алгебраические фракталы
- 11. Пример алгебраического фрактала
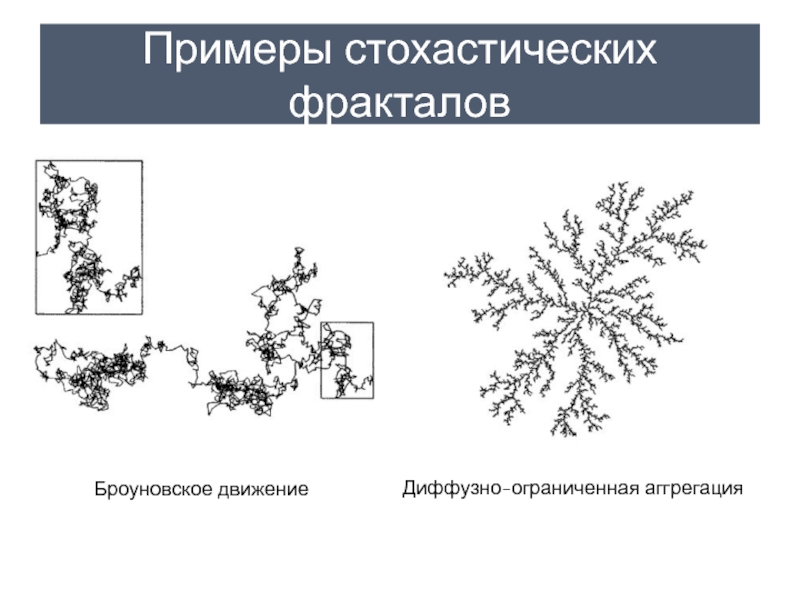
- 12. Стохастические фракталы Стохастические фракталы получаются в том
- 13. Примеры стохастических фракталов Броуновское движение Диффузно-ограниченная аггрегация
- 14. Применение
- 15. Рендеринг реалистичных изображений
- 16. Фрактальное сжатие
- 17. Распознавание образов
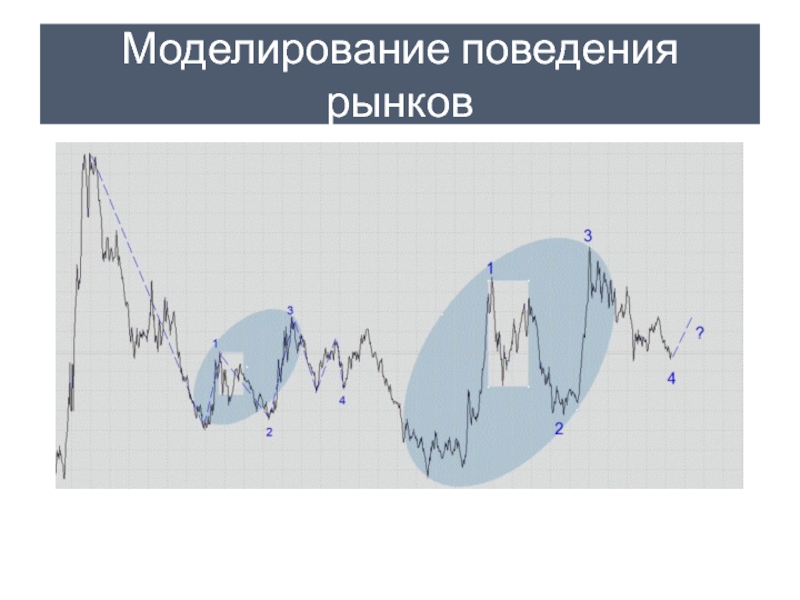
- 18. Моделирование поведения рынков
- 19. Компактные антенны
- 20. Спасибо за внимание
Слайд 2Геометрия природы
Рождение фрактальной геометрии принято связывать
с выходом в 1977 году книги
Мандельброта
"The Fractal Geometry of Nature" ("Фрактальная геометрия природы")
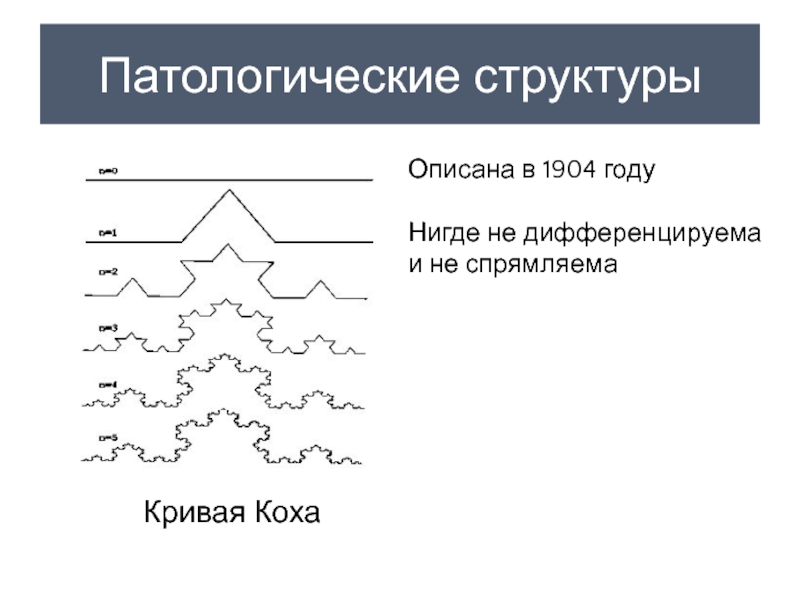
Слайд 5Патологические структуры
Кривая Коха
Описана в 1904 году
Нигде не дифференцируема и не спрямляема
Слайд 6Определение
Фрактал (лат. fractus — дробленый, сломанный, разбитый) — термин, означающий сложную
геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому (Мандельброт)
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому (Мандельброт)
Слайд 8Геометрические фракталы
Самые наглядные
В двумерном случае их получают с помощью некоторой ломаной,
называемой генератором
За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на генератор, в соответствующем масштабе
В результате бесконечного повторения этой процедуры, получается геометрический фрактал
За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на генератор, в соответствующем масштабе
В результате бесконечного повторения этой процедуры, получается геометрический фрактал
Слайд 12Стохастические фракталы
Стохастические фракталы получаются в том случае, если в итерационном процессе
случайным образом менять какие-либо его параметры
Получающиеся объекты очень похожие на природные: несимметричные деревья, изрезанные береговые линии и т.д.
Получающиеся объекты очень похожие на природные: несимметричные деревья, изрезанные береговые линии и т.д.