- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математического анализа презентация
Содержание
- 1. Основы математического анализа
- 2. План курса Основы математической логики и теории
- 3. Элементы математической логики
- 4. Высказывания Высказывание – всякое утверждение, о котором
- 5. Обозначения Высказывания будем обозначать большими латинскими буквами
- 6. Формулы Пусть заданы высказывания X1, X2,…, Xn
- 7. Операции над высказываниями Отрицание Конъюнкция Дизъюнкция Импликация Эквиваленция
- 8. Приоритет операций отрицание ( )
- 9. Отрицание Отрицанием А (обозначается А) называется
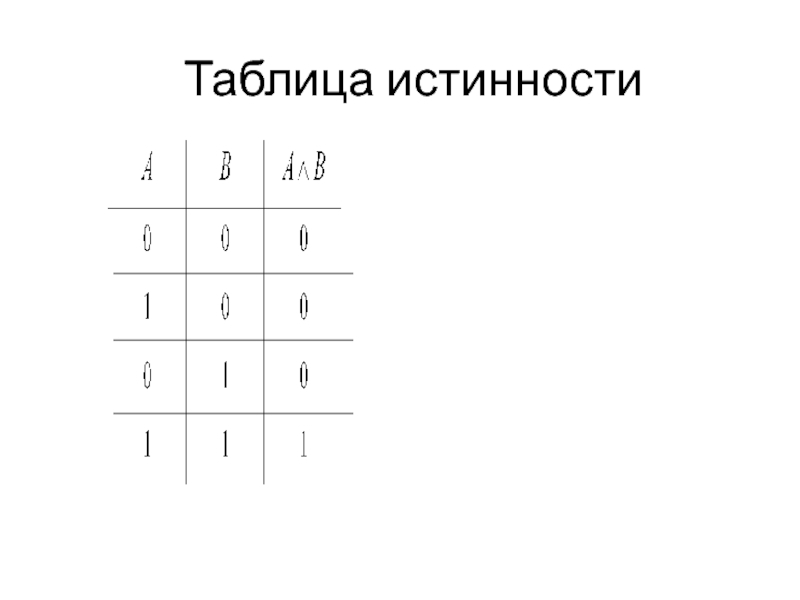
- 10. Конъюнкция Конъюнкцией (от лат. conjunctio – союз,
- 11. Таблица истинности
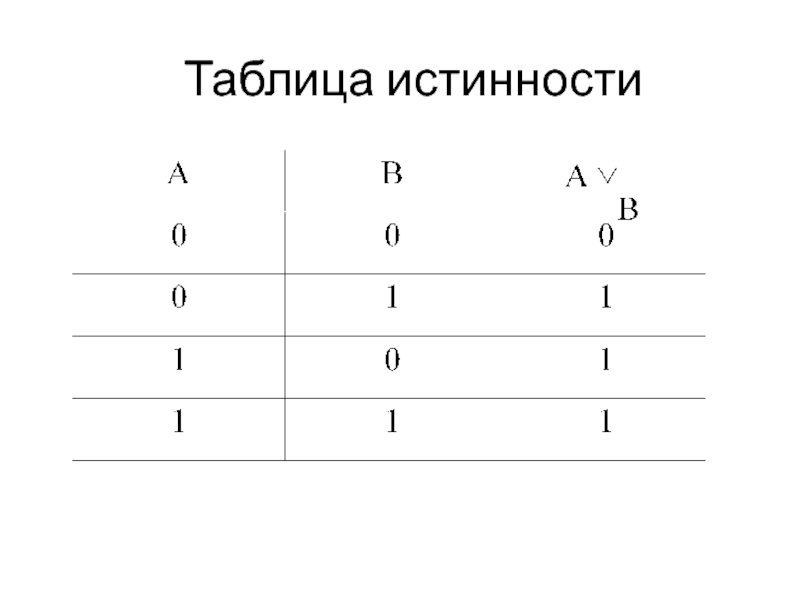
- 12. Дизъюнкция Дизъюнкцией (от лат. disjunctio – различие)
- 13. Таблица истинности
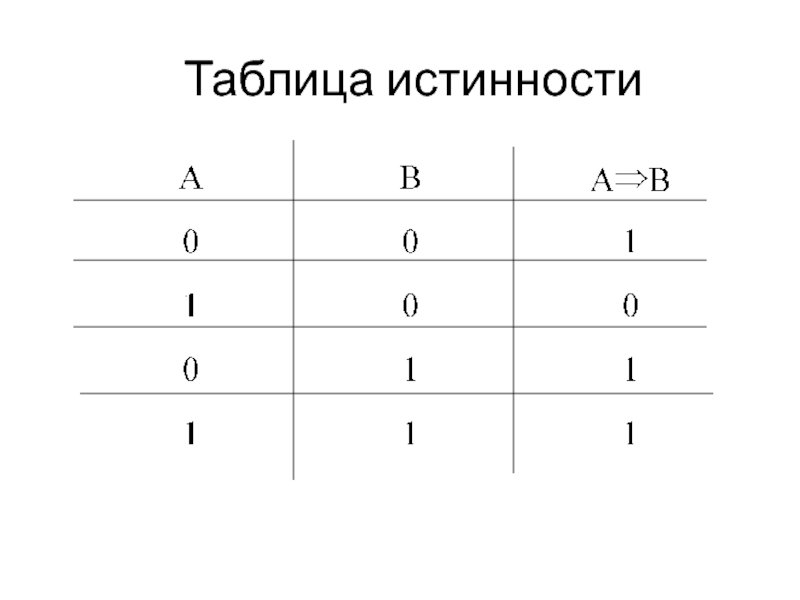
- 14. Импликация Импликацией (от лат. implico – тесно
- 15. Таблица истинности
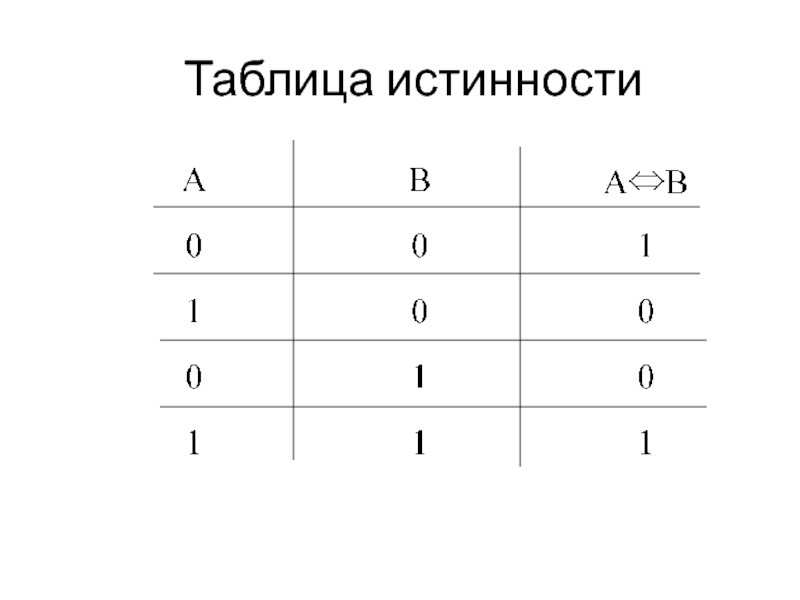
- 16. Эквиваленция Эквиваленцией высказываний А и В называется
- 17. Таблица истинности
- 18. ТИ и ТЛ Формула A (X1, …,
- 19. Логические законы Тождественно истинные высказывания записывают законы,
- 20. Примеры законов X ⇔ X закон тождества
- 21. Формулы A и B называются эквивалентными
- 22. Пример решения задачи 1 Доказать логический закон, используя таблицы истинности: (Х⇒У)⇔ Х ∨ У
- 23. Шаг 1 Строим таблицу истинности для формулы,
- 24. Шаг 2 Строим таблицу истинности для
- 25. Шаг 3 Строим таблицу истинности для формулы
- 26. Шаг 4 Поскольку формула А ⇔В является тождественно истинной, закон доказан.
- 27. Предикат В каждом высказывании есть подлежащее и
- 28. предикат – это функция Р(х), определенная на М со значениями «истина» или «ложь».
- 29. Если в предложении содержится утверждение о
- 30. Кванторы Для того, чтобы характеризовать свойства не
- 31. Переход от P(x) к ∀xP(x) называется
- 32. Переход от P(x) к ∃xP(x) называется
- 33. Пример Определим на множестве N предикат P,
- 34. Элементы теории множеств
- 35. Множество Множество — совокупность определенных различаемых объектов
- 36. Задание множеств перечисление всех элементов множества
- 37. Операции над множествами пересечение объединение разность симметрическая разность
- 38. Пересечение Пересечением множеств A и B
- 39. Объединение Объединением множеств A и B (обозначается
- 40. Разность Разность (дополнение) множеств A и B
- 41. Симметрическая разность Симметрическая разность множеств A и
- 42. Пустое множество (обозначается ∅) есть множество,
- 43. Дополнение Дополнение множества A (обозначается A′)
- 44. Спасибо за внимание!
Слайд 1
Основы математического анализа
Зарубежное регионоведение
1 курс
Сафонова Татьяна Евгеньевна, к.ф.-м.н., доцент
Слайд 2План курса
Основы математической логики и теории множеств
Матрицы и определители
Системы линейных алгебраических
уравнений (СЛАУ)
Формализация бинарных отношений и двухместных предикатов в виде графов
Формализация бинарных отношений и двухместных предикатов в виде графов
Слайд 4Высказывания
Высказывание – всякое утверждение, о котором объективно и определенно можно сказать,
истинно оно или ложно.
Например:
«параллелограмм имеет четыре вершины»,
«число 25 делится на 5»,
«зимой день короче, чем летом».
Например:
«параллелограмм имеет четыре вершины»,
«число 25 делится на 5»,
«зимой день короче, чем летом».
Слайд 5Обозначения
Высказывания будем обозначать большими латинскими буквами
фиксированные высказывания – А, В,
С, …, любые высказывания – X, Y, Z,
значения истинности высказывания – 1 (истина) и 0 (ложь).
значения истинности высказывания – 1 (истина) и 0 (ложь).
Слайд 6Формулы
Пусть заданы высказывания X1, X2,…, Xn
(их можно назвать исходными),
тогда
из них с помощью символов логических операций можно образовать выражения, или формулы.
Например, (X1∨ X2) ⇒ X3,
((X1 ∨ X2) ⇒ X3) ∧ (X1 ∧ X4) и т.п.
Например, (X1∨ X2) ⇒ X3,
((X1 ∨ X2) ⇒ X3) ∧ (X1 ∧ X4) и т.п.
Слайд 8Приоритет операций
отрицание ( )
конъюнкция ( ∧ )
дизъюнкция ( ∨
)
импликация ( ⇒ )
эквиваленция ( ⇔ )
импликация ( ⇒ )
эквиваленция ( ⇔ )
Слайд 9Отрицание
Отрицанием А (обозначается А) называется высказывание ¬ А («не А»),
которое истинно, когда ложно А, и ложно, когда А истинно.
А ¬ А
1 0
0 1
А ¬ А
1 0
0 1
Слайд 10Конъюнкция
Конъюнкцией (от лат. conjunctio – союз, связь) высказываний А и В
называется высказывание А ∧ В
(«А и В»), истинное в том и только в том случае, когда оба высказывания А и В истинны.
(«А и В»), истинное в том и только в том случае, когда оба высказывания А и В истинны.
Слайд 12Дизъюнкция
Дизъюнкцией (от лат. disjunctio – различие) высказываний А и В называется
высказывание А∨В
(«А или В»), ложное в том и только в том случае, когда оба высказывания А и В ложны.
(«А или В»), ложное в том и только в том случае, когда оба высказывания А и В ложны.
Слайд 14Импликация
Импликацией (от лат. implico – тесно связаны) высказываний А и В
называется высказывание А⇒ В
(«А влечет В», «А имплицирует В», ложное в том и только в том случае, когда А истинно, а В ложно.
Еще одно обозначение импликации: А⊃В («если А, то В»).
(«А влечет В», «А имплицирует В», ложное в том и только в том случае, когда А истинно, а В ложно.
Еще одно обозначение импликации: А⊃В («если А, то В»).
Слайд 16Эквиваленция
Эквиваленцией высказываний А и В называется высказывание А⇔В
(«А эквивалентно В»,
«эквиваленция А и В», истинное в том и только в том случае, когда высказывания А и В оба истинны или оба ложны.
Еще одно обозначение: А ~ В («А тогда и только тогда, когда В»).
Еще одно обозначение: А ~ В («А тогда и только тогда, когда В»).
Слайд 18ТИ и ТЛ
Формула A (X1, …, Xn), принимающая для всех значений
из Bn значение 1, называется тождественно истинным (ТИ-) высказыванием, а формула, принимающая для всех значений из Bn значение 0 – тождественно ложным (ТЛ-) высказыванием.
Слайд 19Логические законы
Тождественно истинные высказывания записывают законы, так как они истинны только
в силу своей формы, независимо от содержания исходных высказываний.
Слайд 21
Формулы A и B называются эквивалентными (равносильными), если высказывание A ⇔
B является
ТИ-высказыванием.
ТИ-высказыванием.
Слайд 23Шаг 1
Строим таблицу истинности для формулы, стоящей в левой части (обозначим
ее А):
Х Y А=(Х⇒Y)
1 0 0
1 1 1
0 1 1
0 0 1
Х Y А=(Х⇒Y)
1 0 0
1 1 1
0 1 1
0 0 1
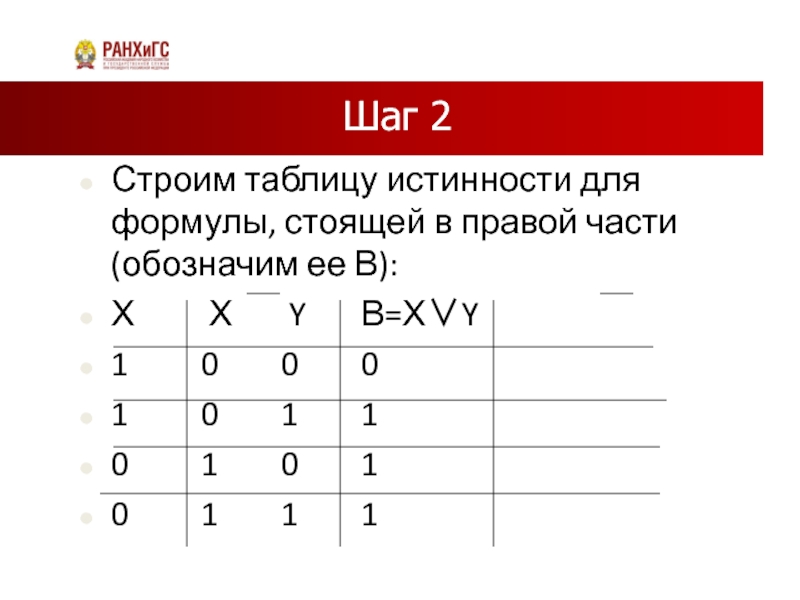
Слайд 24Шаг 2
Строим таблицу истинности для формулы, стоящей в правой части (обозначим
ее В):
Х Х Y В=Х∨Y
1 0 0 0
1 0 1 1
0 1 0 1
0 1 1 1
Х Х Y В=Х∨Y
1 0 0 0
1 0 1 1
0 1 0 1
0 1 1 1
Слайд 25Шаг 3
Строим таблицу истинности для формулы
А ⇔В:
Х Y А В А ⇔В
1 0 0 0 1
1 1 1 1 1
0 1 1 1 1
0 0 1 1 1
Слайд 27Предикат
В каждом высказывании есть подлежащее и сказуемое, т.е. объект и предикат
(свойство объекта).
Множество объектов, для которых может быть определен данный предикат, образуют поле предиката М.
Множество объектов, для которых может быть определен данный предикат, образуют поле предиката М.
Слайд 29
Если в предложении содержится утверждение о нескольких объектах и отношениях между
ними, то оно может быть записано с использованием многоместного предиката.
Например, высказывание «3 > 0» («3 больше 0») может быть формализовано не только с помощью одноместного предиката Р(х) («х > 0»), но и двухместного предиката Р(х, у) («х > y»).
Например, высказывание «3 > 0» («3 больше 0») может быть формализовано не только с помощью одноместного предиката Р(х) («х > 0»), но и двухместного предиката Р(х, у) («х > y»).
Слайд 30Кванторы
Для того, чтобы характеризовать свойства не каждого отдельного объекта, а всей
их совокупности (всего поля предиката), используются кванторы.
квантор общности (обозначается ∀) и квантор существования (обозначается ∃)
квантор общности (обозначается ∀) и квантор существования (обозначается ∃)
Слайд 31
Переход от P(x) к ∀xP(x) называется навешиванием квантора общности по предметной
переменной x.
При этом переходе предикату P(x) ставится в соответствие высказывание ∀xP(x) (читается: «для всякого x имеет место P(x)»), которое по определению является истинным тогда и только тогда,
когда высказывание P(a) истинно для любого a∈ M.
При этом переходе предикату P(x) ставится в соответствие высказывание ∀xP(x) (читается: «для всякого x имеет место P(x)»), которое по определению является истинным тогда и только тогда,
когда высказывание P(a) истинно для любого a∈ M.
Слайд 32
Переход от P(x) к ∃xP(x) называется навешиванием квантора существования по предметной
переменной x.
При этом переходе предикату P(x) ставится в соответствие высказывание ∃xP(x)
(читается: «существует такое x, что имеет место P(x)»), которое по определению является истинным тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного a∈ M.
При этом переходе предикату P(x) ставится в соответствие высказывание ∃xP(x)
(читается: «существует такое x, что имеет место P(x)»), которое по определению является истинным тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного a∈ M.
Слайд 33Пример
Определим на множестве N предикат P, полагая P(a)=1 тогда и только
тогда, когда a – простое.
Тогда ∀xP(x) есть высказывание «всякое натуральное число является простым» (ложное),
∃xP(x) – «существует натуральное число, являющееся простым» (истинное).
Тогда ∀xP(x) есть высказывание «всякое натуральное число является простым» (ложное),
∃xP(x) – «существует натуральное число, являющееся простым» (истинное).
Слайд 35Множество
Множество — совокупность определенных различаемых объектов таких, что для любого объекта
можно установить, принадлежит этот объект данному множеству или нет.
Множества обозначаются прописными буквами: A, B, C ..., элементы – строчными буквами: x, y, z, …
Множества обозначаются прописными буквами: A, B, C ..., элементы – строчными буквами: x, y, z, …
Слайд 36Задание множеств
перечисление всех элементов множества
A= {7, 8, 9}
указание свойств элементов
множества
A={x: x — целое число и 6 < x < 10}
x ∈ A
x ∉ A
A={x: x — целое число и 6 < x < 10}
x ∈ A
x ∉ A
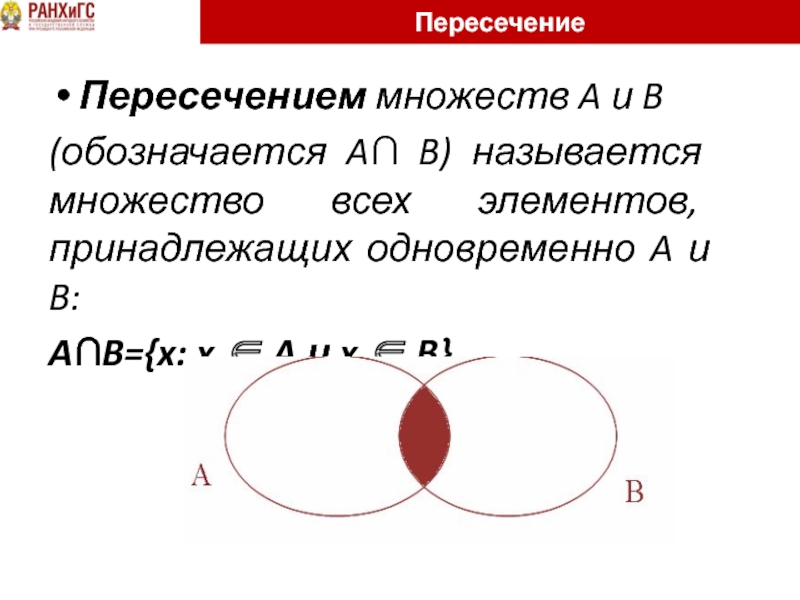
Слайд 38Пересечение
Пересечением множеств A и B
(обозначается A∩ B) называется множество всех
элементов, принадлежащих одновременно A и B:
A∩B={x: x ∈ A и x ∈ B}.
A∩B={x: x ∈ A и x ∈ B}.
Слайд 39Объединение
Объединением множеств A и B (обозначается A∪B) называется множество всех элементов,
принадлежащих либо A, либо B, либо одновременно и A и B:
A∪B={x: x ∈ A или x ∈ B}.
A∪B={x: x ∈ A или x ∈ B}.
Слайд 40Разность
Разность (дополнение) множеств A и B (записывается в виде A \
B) — множество элементов, принадлежащих A и не принадлежащих B:
A \ B ={x: x∈A и x∉B} (дополнение B до A).
A \ B ={x: x∈A и x∉B} (дополнение B до A).
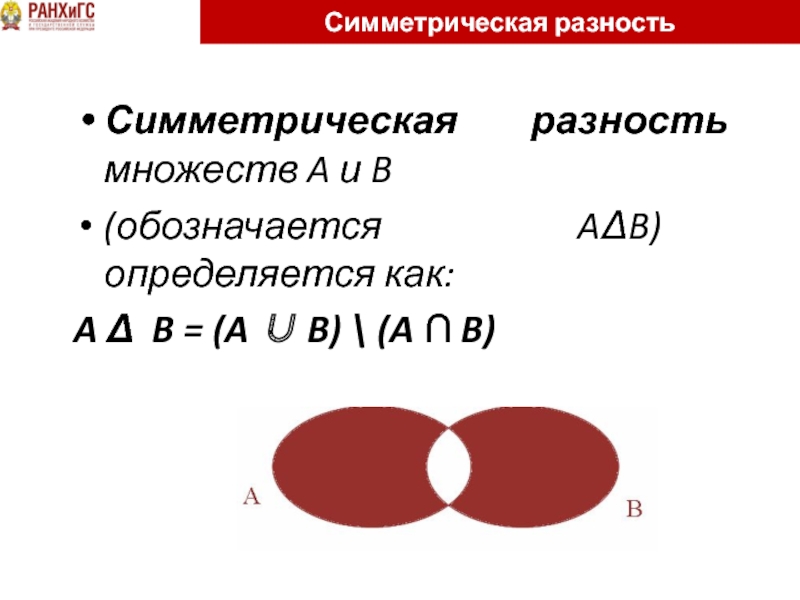
Слайд 41Симметрическая разность
Симметрическая разность множеств A и B
(обозначается AΔB) определяется как:
A Δ B = (A ∪ B) \ (A ∩ B)
Слайд 42
Пустое множество (обозначается ∅) есть множество, обладающее свойством: x ∉ ∅
при любом x.
Универсальное множество (обозначается E) есть множество всех рассматриваемых в данной задаче элементов.
Универсальное множество (обозначается E) есть множество всех рассматриваемых в данной задаче элементов.