- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы дисперсионного анализа презентация
Содержание
- 1. Основы дисперсионного анализа
- 2. План лекции: Актуальность темы. Виды дисперсионного анализа
- 3. Актуальность темы Основной целью дисперсионного анализа
- 4. Нулевая гипотеза: В генеральной совокупности групповые
- 5. Условия: изучаемые факторы должны быть независимыми;
- 6. Виды дисперсионного анализа и его характеристики
- 7. Признаки, изменяющиеся под влиянием тех или иных
- 8. При однофакторном ANOVA изучается влияние одного фактора
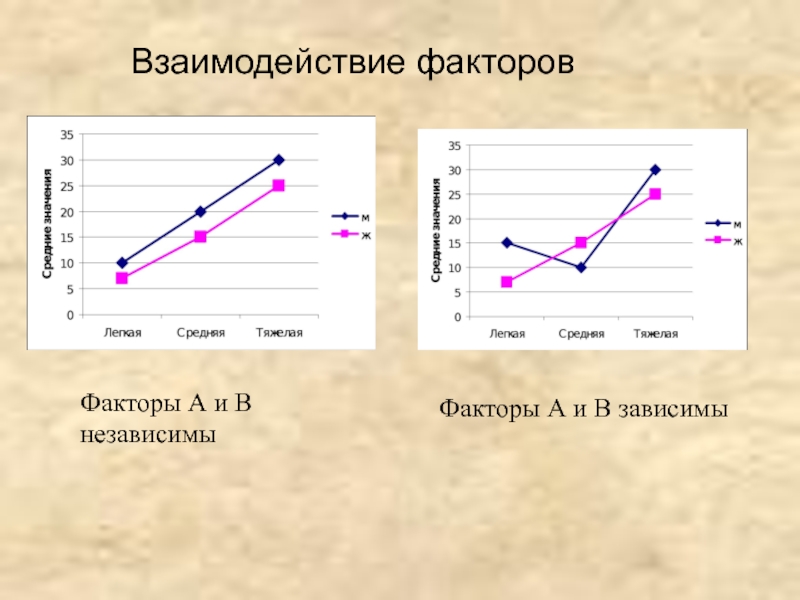
- 9. Взаимодействие факторов Факторы А и В независимы Факторы А и В зависимы
- 10. Пример: трехфакторный ANOVA. Факторы А, В, С.
- 11. Dобщ = Dфакт + Dслуч -
- 12. Этапы дисперсионного анализа: Представить данные в виде
- 13. Общее варьирование всех вариант (хij), независимо от
- 14. Варьирование групповых средних или средних
- 15. Варьирование вариант хij внутри каждой группы вокруг
- 16. Формулы для однофакторного дисперсионного анализа
- 17. Пример. Провести однофакторный дисперсионный анализ для выяснения
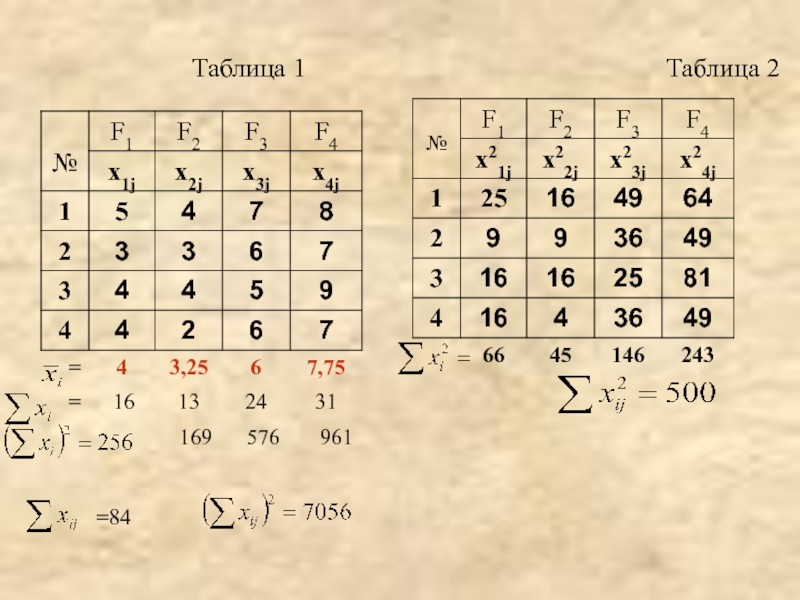
- 18. Таблица 1
- 19. Вычисления: Сумма квадратов SSобщ для общей вариации:
- 20. Сумма квадратов SSсл для вариации внутри групп:
- 21. Сила влияния фактора Сила влияния фактора
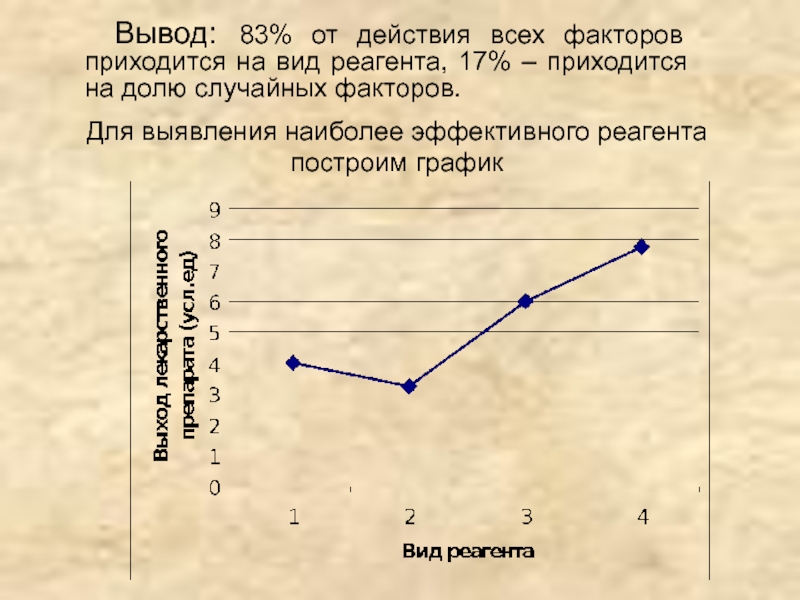
- 22. Вывод: 83% от действия всех
- 23. Множественные сравнения Дисперсионный анализ позволяет установить, существуют
- 24. Коэффициент Q, рассчитан для разного количества групп
- 25. Вывод: Вид реагента достоверно влияет
- 26. Множественные сравнения Поправка Бонферрони если имеется n
- 27. Заключение Таким образом, нами
- 28. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Попов А.М. Теория
- 29. БЛАГОДАРЮ ЗА ВНИМАНИЕ
Слайд 1ОСНОВЫ ДИСПЕРСИОННОГО
АНАЛИЗА
Лекция №9
для студентов 2 курса,
обучающихся по специальности 060609
доц. Шапиро Л.А.
Красноярск, 2015 г.
Слайд 2План лекции:
Актуальность темы.
Виды дисперсионного анализа и его характеристики
Этапы дисперсионного анализа
Формулы
Сила влияния фактора
Множественные сравнения.
Слайд 3Актуальность темы
Основной целью дисперсионного анализа является исследование значимости различия между
Слайд 4
Нулевая гипотеза:
В генеральной совокупности групповые средние нормальных совокупностей с одинаковыми дисперсиями
Для проверки этой нулевой гипотезы достаточно проверить по критерию Фишера нулевую гипотезу о равенстве факторной и случайной дисперсии
(в этом состоит метод ДА)
Слайд 5Условия:
изучаемые факторы должны быть независимыми;
распределение выборочных данных должно соответствовать нормальному
Выборки однородны - выборочные дисперсии не различаются значимо (критерии Кочрена, Левене, Бартлета и т.д.)
х – μ =А+е, где μ – средняя арифметическая генеральной совокупности;
х – конкретное значение переменной;
А – доля отклонения переменной, связанная с влиянием данного конкретного фактора;
е – остаточная часть отклонения, не объяснимая влиянием данного фактора.
Слайд 6Виды дисперсионного анализа и его характеристики
Раздел статистики, изучающий влияние
Д.А. повторных наблюдений.
Д.А. независимых выборок .
Многомерный Д.А.
Слайд 7Признаки, изменяющиеся под влиянием тех или иных причин, называются результативными (зависимыми).
Сами
Конкретное значение фактора называется градацией (или уровнем) фактора (доза препарата, степень тяжести заболевания).
Градациям (уровням) межгруппового фактора соответствуют независимые выборки объектов.
Градациям (уровням) внутригруппового фактора соответствуют зависимые выборки объектов (повторные измерения).
Слайд 8При однофакторном ANOVA изучается влияние одного фактора на зависимую переменную. Проверяется
Многофакторный ANOVA позволяет проверять гипотезы не только о влиянии каждого фактора в отдельности, но и о взаимодействии факторов.
Пример: двухфакторный ANOVA. Изучается влияние двух факторов А-степень тяжести заболевания, B – пол на содержание гемоглобина. Проверяется три гипотезы:
1. Влияние степени тяжести заболевания (А).
2. Влияние гендерных различий (В).
3. Взаимодействие факторов АВ (зависимость степени влияния одного фактора от градаций другого).
Слайд 10Пример: трехфакторный ANOVA. Факторы А, В, С. Проверяется семь гипотез:
А
Двухфакторный ANOVA с повторными измерениями по одному из факторов проверяются три гипотезы:
Влияние внутригруппового фактора.
2. Влияние межгруппового фактора.
3. Взаимодействие внутригруппового и межгруппового фактора.
Степень изменения всех признаков и отклонение их от средней арифметической ряда характеризуется дисперсией D(х):
D(X)=M(X2)-(M(X))2
Слайд 11Dобщ = Dфакт + Dслуч
- критерий Фишера
Если F>Fкр
Если F
Однофакторный дисперсионный анализ.
Идея метода - разложить показатель изменчивости признака на две составляющие: изменчивость между группами и изменчивость внутри групп.
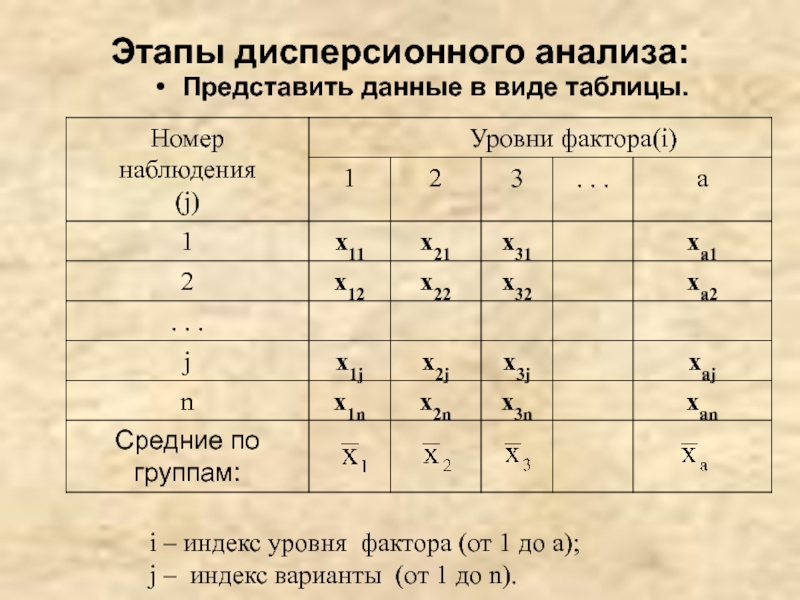
Слайд 12Этапы дисперсионного анализа:
Представить данные в виде таблицы.
i –
j – индекс варианты (от 1 до n).
Слайд 13Общее варьирование всех вариант (хij), независимо от того, в какой группе
где N=a∙n– число всех вариант;
dfобщ.= N–1 – число степеней свободы.
Слайд 14Варьирование групповых средних или средних каждого уровня данного изучаемого
dfфакт= a – 1– число степеней свободы.
ni – среднее число вариант в каждой группе,
n – если число вариант в группах одинаково.
Слайд 15Варьирование вариант хij внутри каждой группы вокруг каждой групповой средней
df случ =N - a – число степеней свободы.
Причем: (N – a) + (a – 1) = N – 1
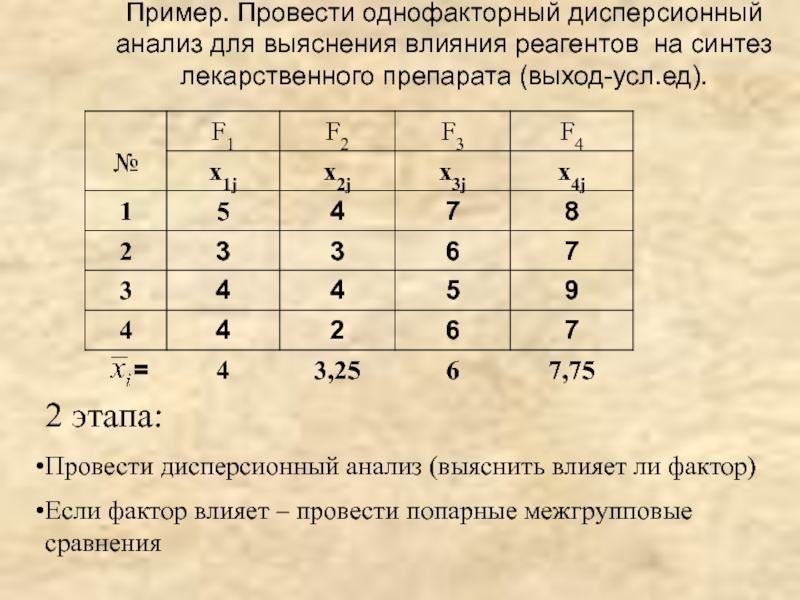
Слайд 17Пример. Провести однофакторный дисперсионный анализ для выяснения влияния реагентов на синтез
2 этапа:
Провести дисперсионный анализ (выяснить влияет ли фактор)
Если фактор влияет – провести попарные межгрупповые сравнения
Слайд 19Вычисления:
Сумма квадратов SSобщ для общей вариации:
Сумма квадратов SSфакт для вариации между
Средний квадрат, характеризующий факторную дисперсию MSфакт:
(
)
(
)
.
49.5
16
7056
1962
4
1
1
2
2
=
−
=
−
=
е
е
е
N
x
x
n
SS
ij
i
фак
Слайд 20Сумма квадратов SSсл для вариации внутри групп:
Средний квадрат MSсл для вариации
SSсл=SSобщ – SSфак = 59 – 49,5=9,5
т.к MSсл< MSфак,
а Fкрит=3,49 для α=0,05 и dfсл=12 и dfфак=3
ВЛИЯНИЕ ФАКТОРА ДОСТОВЕРНО!
Слайд 22 Вывод: 83% от действия всех факторов приходится на вид
Для выявления наиболее эффективного реагента построим график
Слайд 23Множественные сравнения
Дисперсионный анализ позволяет установить, существуют ли достоверные различия между отдельными
Между какими группами конкретно имеется разница - необходимо выяснить.
n – число вариант в каждой группе.
Отношение разницы d к ее ошибке Sd , т.е. должно быть таким, чтобы оно гарантировало значимость не менее чем при α=0,05.
Слайд 24Коэффициент Q, рассчитан для разного количества групп а и степеней свободы
d12=4-3,25=0,7; d23=6-3,25=2,75;
Q=4,2 для dfслуч=12 и а=4;
t12< Q, разница не достоверна
t23> Q, разница достоверна
Слайд 25Вывод:
Вид реагента достоверно влияет на выход лекарственного препарата. Наибольшую
Слайд 26Множественные сравнения
Поправка Бонферрони
если имеется n групп, то уровень значимости
например, при n=3
Критерии:
LSD (наименьшей значимой разности)
Ньюмена-Кейлса
Шеффе
Тьюки и т.д.
Слайд 27Заключение
Таким образом, нами рассмотрены основы дисперсионного анализа, изучающего
Слайд 28РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
Основная литература:
Попов А.М. Теория вероятней и математическая статистика /А.М. Попов,
Герасимов А. Н. Медицинская статистика: учебное пособие / А. Н. Герасимов. – М. : Мед. информ. агентство, 2007. – 480 с.
Балдин К. В. Основы теории вероятностей и математической статистики : учебник / К. В. Балдин. – М. : Флинта, 2010. – 488с.
Учебно–методические пособия:
Шапиро Л.А., Шилина Н.Г. Руководство к практическим занятиям по медицинской и биологической статистике Красноярск: ООО «Поликом». – 2003.