- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные теоремы дифференциального исчисления презентация
Содержание
- 1. Основные теоремы дифференциального исчисления
- 2. Доказательство: Пусть функция y=f(x) дифференцируема на промежутке
- 3. и По условию функция y=f(x) дифференцируема в
- 4. Геометрический смысл теоремы Ферма В точке
- 5. Теорема Ролля Пусть функция y=f(x)
- 6. Доказательство: По теореме Вейерштрасса, функция, непрерывная на
- 7. Геометрический смысл теоремы Ролля Найдется хотя
- 9. Если же хотя бы одно условие теоремы
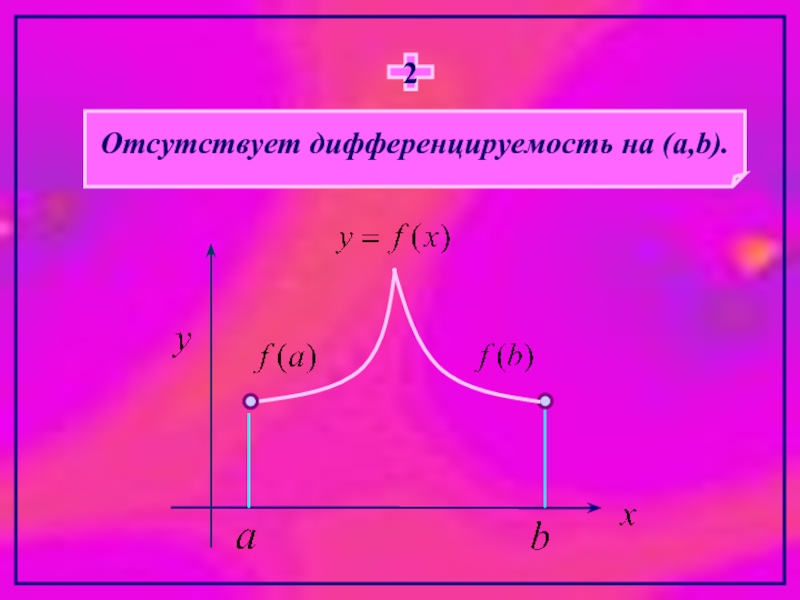
- 10. Отсутствует дифференцируемость на (a,b). 2
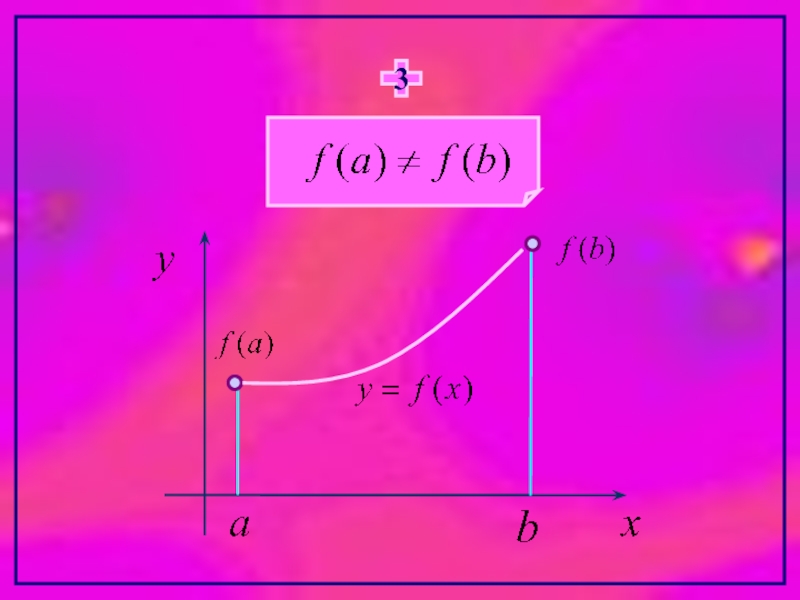
- 11. 3
- 12. Теорема Лагранжа Пусть функция y=f(x)
- 13. Тогда внутри отрезка существует по крайней
- 14. Доказательство: Введем новую функцию g(x): Эта функция
- 15. Следовательно, по теореме Ролля существует точка такая, что
- 16. или отсюда
- 17. Эту теорему часто записывают в виде:
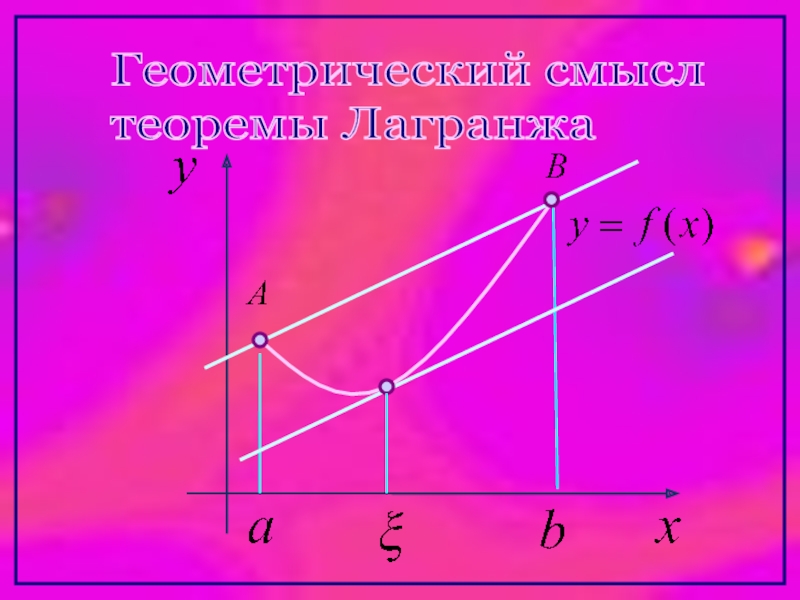
- 18. Геометрический смысл теоремы Лагранжа
- 19. Если перемещать прямую АВ параллельно начальному
- 20. Следствие. Если производная функции y=f(x)
- 21. Доказательство: Возьмем на промежутке Х [a,х], тогда
Слайд 18.9. ОСНОВНЫЕ ТЕОРЕМЫ
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Теорема Ферма
Если дифференцируемая на промежутке Х функция
Слайд 2Доказательство:
Пусть функция y=f(x) дифференцируема на промежутке Х и в точке
принимает
Тогда
если
Величина
Следовательно
при
при
Слайд 3и
По условию функция y=f(x) дифференцируема в точке х0, следовательно ее предел
Переходим в этих неравенствах соответственно к пределу справа и слева:
не должен зависеть от способа стремления Δх к нулю, т.е.
Слайд 4Геометрический смысл
теоремы Ферма
В точке наибольшего или наименьшего
значения, достигаемого внутри
Х, касательная к графику функции
параллельна оси Х.
Слайд 5Теорема Ролля
Пусть функция y=f(x) удовлетворяет следующим условиям:
Непрерывна на отрезке
Дифференцируема на интервале (a,b).
На концах отрезка принимает равные значения: f(a)=f(b).
Тогда внутри отрезка существует по крайней мере одна такая точка ξ, в которой производная равна нулю:
Слайд 6Доказательство:
По теореме Вейерштрасса, функция, непрерывная на отрезке, достигает на нем своего
Если оба этих значения достигаются на концах отрезка,то они по условию равны: М= m, а это значит, что функция постоянна на [a,b]. Тогда
во всех точках этого отрезка.
Если же хотя бы одно из этих значений достигается внутри отрезка, то по теореме Ферма, производная функции в этой точке равна нулю:
Слайд 7Геометрический смысл
теоремы Ролля
Найдется хотя бы одна точка, в которой
касательная к
параллельна оси Х, в этой точке
производная функции будет равна нулю.
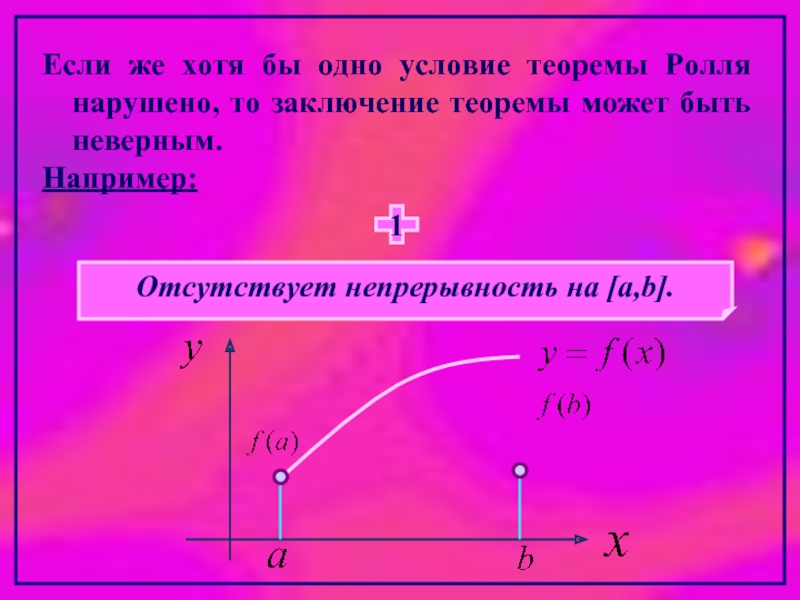
Слайд 9Если же хотя бы одно условие теоремы Ролля нарушено, то заключение
Например:
Отсутствует непрерывность на [a,b].
1
Слайд 12Теорема Лагранжа
Пусть функция y=f(x) удовлетворяет следующим условиям:
Непрерывна на отрезке
Дифференцируема на интервале (a,b).
Слайд 13
Тогда внутри отрезка существует по крайней мере одна такая точка ξ,
Слайд 14Доказательство:
Введем новую функцию g(x):
Эта функция удовлетворяет всем условиям теоремы Ролля:
Она
Слайд 19
Если перемещать прямую АВ параллельно начальному положению, то найдется хотя бы
в которой касательная к графику функции y=f(x) и хорда АВ, проведенная через концы дуги АВ будут параллельны.
Слайд 20Следствие.
Если производная функции y=f(x) равна 0 на некотором промежутке Х,
Слайд 21Доказательство:
Возьмем на промежутке Х [a,х], тогда по теореме Лагранжа
По условию теоремы
То




![Теорема Ролля Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b].Дифференцируема на интервале (a,b).На](/img/tmb/2/119236/c106ee326e6ab361f826feac281aa407-800x.jpg)


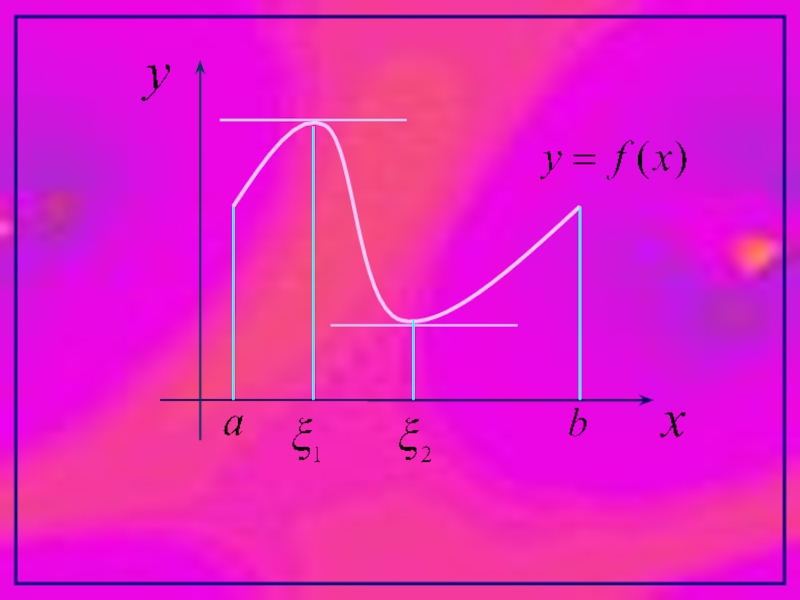
![Теорема Лагранжа Пусть функция y=f(x) удовлетворяет следующим условиям: Непрерывна на отрезке [a,b].Дифференцируема на интервале (a,b).](/img/tmb/2/119236/f16b5572cf6cec8b41eb0ec5a79abc8e-800x.jpg)

![Доказательство:Введем новую функцию g(x):Эта функция удовлетворяет всем условиям теоремы Ролля: Она непрерывна на [a,b], дифференцируема](/img/tmb/2/119236/3bec421526adbbece1bd8c7add69317a-800x.jpg)





![Доказательство:Возьмем на промежутке Х [a,х], тогда по теореме ЛагранжаПо условию теоремыТо есть](/img/tmb/2/119236/a8c37517a0a41418275f0cdb60338877-800x.jpg)